城镇地价的空间分布格局研究——以免渡河镇为例



城镇地价的空间分布格局研究——以免渡河镇为例

胡 君 德1，李 百 岁1，张婷2，谷 俊 杰1

(1.内蒙古师范大学 地理科学学院，呼和浩特 010022，2.内蒙古大学 生命科学学院， 呼和浩特 010021)

摘要：基于地统计学方法及其相关理论，以免渡河为例，研究城镇地价的分布格局，并运用空间自相关和Kriging插值法分析方法进一步揭示了城镇地价的空间分异特征和空间集聚分布规律。本文数据源自免渡河镇2012年土地分等定级及基准地价更新。采用Moran’sI、Getis’ G指数和地统计学中的半变异性方法对免渡河镇的商业和住宅地价的全局自相关与局域自相关及各项异性进行全面分析，并运用Kriging插值法与空间自相关对比分析，且均采用球状模型曲线得出：免渡河镇的地价在1700米的范围内均存在正相关及高聚集性，随着距离的增大，自相关性逐步减弱，地价的空间自相关在各个方向都不径相同，且在部分区域表现有异质性。在西北-东南方向地价的空间自相关范围要大于东北—西南方向，且随机性较强，如商业地价在此方向的的自相关变化程度较大。

关键词：城镇地价；空间自相关；半变异函数；Kriging插值；各项异性

随着改革开放的不断推进，房地产市场经济在市场经济中扮演着日趋重要的角色，并长期受到社会各界的广泛关注。土地价格是反映土地市场供需的“晴雨表”。地价的空间特性也完全符合Tobler地理学第一定律，即地理事物或属性在空间分布上互为相关，存在集聚、随机和规则分布，且距离越近，空间关联性越强[1]。空间地价的研究主要通过时间演变规律[2-3]、GIS空间插值及地统计软件研究地价的空间分布及格局[4-7]和计量经济研究城市地价空间[8-9]。地价理论是随着地租理论的发展而不断发展的，随着科学技术的不断发展，大量的空间分析功能被集成到GIS和地统计软件中，空间分析技术在地价研究中得到广泛应用。

近些年有一些学者对地价进行了研究，主要是利用GIS插值和空间自相关性对地价分布的空间格局及分异规律的探索做了大量工作。焦利民等研究了区域城镇基准地价水平的空间自相关格局[10]；蒋芳和马敏蕾等在基于GIS的研究基础上对北京市住房价格进行了探讨。[11-12]公云龙等研究了宿州市城市地价的自相关性[13]；魏晓峰等研究了基于ArcGIS的空间自相关分析模块的开发与应用[14]；梅志雄等研究了东莞的房地产价格的全局与局域空间自相关性[15]。

本文研究区位于呼伦贝尔市免渡河镇，是呼伦贝尔市重要的交通枢纽和能源供应基地。土地是其经济来源的重要支撑，所以研究土地价格的空间分布规律就显得尤为重要。主要运用GIS的空间分析和地统计软件对免渡河镇商业与住房地价的空间分布与特征进行研究，整合城镇地价的全局与局域空间自相关性、半变异性分异规律和GIS的Kriging插值等方法，展开对免渡河镇的地价进行探索。主要研究：(1)全局空间自相关性Moran’sI指数和Getis’ G指数；(2)局域Moran’sI集聚图的生成；(3)半变异函数对空间地价的影响范围；(4)GIS的Kriging插值估算免渡河镇的地价分布格局。

1研究方法

1.1全局统计量

全局统计量试图从整体上反应某一区域变量观测值对地区的影响，检验某种地理现象与属性的集聚程度与规模效应。

1.1.1Moran’sI指数

在给定地价要素及相关属性的情况下，该指数评估所表达的模式是聚类模式、离散模式还是随机模式。通过计算Moran's I 指数值、z得分和p值来对该指数的显著性进行评估。P值是根据已知分布的曲线得出的面积近似值(受检验统计量限制)。

1.1.2Getis’G指数

Getis’G指数一般被用来判断地价要素变量是处在高值聚集区还是低值聚集区，统计学上的显著性热点，地价要素应具有高值，且被其他同样具有高值的要素包围。地价要素及其相邻要素的局部总和将与所有要素的总和成比例地进行比较；当此局部总和与预期的局部总和有很大差异，以致于无法成为随机产生的结果时，会产生一个统计学上的显著性z?得分。Getis’G指数一般采用距离权重。

1.2局域统计量

全局统计量的Moran’sI指数和Getis’G指数，揭示了空间相似属性的集聚程度，但却不能反映不同水平与性质的空间异质性，Anselin提出的空间联系局域指标LISA(Local Indicators of Spatial Association)，可以度量每个单元与邻近单元的之间的局域相关程度。局域自相关能更好的反映空间异质性的范围与位置。其计算公式如下：

1.3地统计学方法

1.3.1半变异函数

地统计学的理论基础是区域化变量理论，主要研究分布于空间并显示出一定结构性和随机性的自然现象。变异函数又称变差函数、变异矩，是以区域化变量理论为基础建设起来的，是地统计分析特有的基本工具。Z(x)是系统某属性Z在空间位置x处的值，Z(x)为一区域化随机变量，并满足二阶平稳假设，h为两样本点空间分隔距离Z(xi)和Z(xi+h)分别是区域化变量Z(x)在空间位置xi和xi+h处的实测值[i=1,2,…,N(h)]，那么，变异函数r(h)的离散计算公式为：

变异函数揭示了在整个尺度上的空间变异格局，而且变异函数只有在最大间隔距离1/2之内才有意义。

1.4Kriging插值

Kriging插值法是对空间分布的数据求线性最优无偏内插估计的一种方法，是利用已知点对未知点进行的一种线性无偏最优估计[16]。

2免渡河镇地价研究

2.1研究区概况及数据来源

免渡河镇，位于祖国的北陲，大兴安岭的西北麓，牙克石市的中部，距市区33公里，镇位于北纬48°46′～49°27′，东经120°42′～122°05′。全镇面积4137.5平方公里，其中镇区8万平方公里。

此次研究数据来源于2012年免渡河镇土地分等定级与基准地价更新，选取商业样点121个，住宅样点196个。

2.2数据的预处理

为使本次研究数据更加可靠准确，采用直方图离群值法选取本次样点，得到有效商业样点102个，住宅样点177个，运用ArcGIS建立空间地理数据库。由于研究的需要，还需将选取的样点经过log函数变换后使它更符合样点的正态分布。

全局和局域统计通常用面状要素反映其变化量的值，而点状要素很难体现样点的分布，所以生成voronoi图就显的尤为的重要。它是一种连续的泰森多边型，能让样点更加清晰直观的反映。

2.3免渡河镇地价空间分布格局分析

2.3.1空间权重的选择

分析地价样点的权重对于研究地价的空间分布具有十分重要的意义，权重选择的好坏、合适与否直接关系到地价数据模拟的准确性。确立权重时采用与距离相关的权重方式反距离法(inverse Disdance)，即与远处的要素相比，附近的邻近要素对目标要素的计算影响要大一些。在一定空间范围内，设置一定的距离d，当要素i和j在距离d以内时，wi,j为1，当不在距离d以内时，wi,j为0，本文以200米为步长，在城镇[100m，2900m]空间范围内依次截取步长。

然而通过距离选取的步长只能从全局上反映样点的空间分布，具体到某些区域地价样点却无法正确的反映地价样点的空间分布邻近的关系，所以在局域范围内运用6个邻居k-nearest的距离权重对地价进行研究能更好的反映地价的空间集聚性。

2.3.2免渡河镇全局空间自相关分析

本研究中主要体现的是Moran’sI指数和Getis’G指数，运用ArcGIS计算其空间分布指数，局域自相关Moran’sI指数使用Geoda095i软件创造6个邻居k-nearest的距离权重，并生成空间滞后向量。半变异方差分析辅以GS+9.0环境科学地统计软件进行研究。其统计结果见表1。

表1:全局空间自相关统计结果

依据2012年免渡河基准地价更新样点资料可知，采用6个邻居k-nearest的距离权重进行计算，本文收集的样点成不规则分布，且面积较大的单元邻接的单元个数少，而面积较小的单元邻接的单元个数较多。由表1可知，在避免“岛”的情况下，每个商业和住宅地价样点的门槛值分别为119m和147m。

住宅的Global Moran's I指数为0.939，经过log变换的z值统计量为15.642，远超过正态分布置信区间99%的距离阈值2.17，在显著性水平为1%情况下，充分说明了其总体水平具有正相关性。同样，经过计算可知，商业价格的Global Moran's I指数为0.474，z值统计量为10.369，大于正态分布置信区间99%的距离阈值2.17，在显著性水平达到1%时全局相关性较强，充分说明了其总体水平具有正相关性。

由本文研究Moran’sI的统计量(P≤0.05)可知，商业样点与住宅样点在一定的范围内均呈正相关，在避免“岛”的情况下，商业地价样点的Moran's I指数最大为0.315，住宅地价样点的Moran's I指数达到了0.514，住宅样点的相关性指数大于商业样点的相关性指数，与6个邻居k-nearest的距离权重下的结果一致，说明在一定范围内，商业样点分布具有不规则性，而住宅样点虽然分布的相关性很高，但某些阈值范围内Moran's I指数变幅较大，存在不稳定性。

如表1，受地理学第一定律的影响，地理事物或属性在空间分布上互为相关，存在集聚、随机和规则分布，且距离越近，空间关联性越强，相反，距离越远空间关联性较弱。商业地价空间自相关性在1700m时接近0，空间相关性很微弱，表现为随机分布，自1700m后Moran’sI指数表现为负数，说明自1700m后商业样点空间相关性不显著，且随着距离的增大，商业地价不具有相关性。由此，可判断商业空间自相关性的阈值范围为1700m。同样，可以明显看到住宅地价的空间自相关性在1900m时接近于0，在1700m时仍具有很小的空间自相关性，但Getis’G指数此时仍表现为高值，与Moran’sI指数相异。而研究表明，Moran’sI指数在判断空间集聚性时更为可靠。因此，判断全局空间自相关程度时往往以Moran’sI指数为主要判断依据。

2.3.3免渡河镇局域空间自相关性

研究局域空间自相关性的意义在于，全局空间自相关性可以从整体镇域的尺度上完成空间其集聚程度和空间自相关性的判断，且绝大部分是在同质为假设基础上完成的，并不能反映某个具体位置的空间相关性。而局域空间自相关性可以研究不同性质与水平的区域空间自相关性。并且局域空间自相关性对于空间异质性的体现也很明显，能够给出准确的位置与范围。

图1:局域Moran’sI指数图

图2:商业和住宅的LISA图

Moran’sI指数图中的横轴表示样点地价均价的标准化值，而纵轴则代表Geoda095i软件生成的空间滞后值，对于空间权重的确立，采用6个邻居k-nearest的距离权重，分别得到住宅和商业的空间权重后，近能得到空间滞后值。

图1分别为局域商业Moran’sI指数和住宅Moran’sI指数图，由住宅Moran’sI指数为0.9394可知，住宅地价的局域集聚性要明显的强于商业的集聚性，在局域范围上住宅的空间自相关性更为明显。绝大部分样点均分布在第一象限和第三象限，说明免渡河镇在商业和住宅在局域空间尺度上相关性程度很高。在第一象限的高值集聚区(HH)，价格高的区域互为邻接，这部分区域无论是商业还是住宅均在免渡河镇区的最中心中央街，其中东中央街全长1520m，宽18m，西中央街全长1600m，宽为16m，镇内主要商业和住房沿街分布，基础设施完备，火车站、汽车站都位于其附近，交通便捷，充分体现了小城镇经济发展和人口分布的特点。第三象限为低值集聚区(LL)，这部分区域通常分布在城镇与郊区相接壤的部分，位于城镇的边缘，属于商业欠发达区域，住房价格相对城镇中心要便宜很多。第二象限和第四象限分别为低高集聚区(LH)和高低集聚区(HL)，而高低集聚区(HL)在Moran’sI指数图上分布很少，且在LISA局域集聚图上不显示，如图2。说明其空间集聚性可以忽略不计。而在低高集聚区(LH)在LISA中只出现在城市中心向外延伸的边缘。因此，我们可以得到免渡河镇的局域空间相关性很高，且商业和住宅都很少出现空间异质性。

2.3.4免渡河镇半变异函数下的地价分布

全局空间自相关性可以判断总体上的集聚程度，但却不能在持续距离的空间尺度上判断其空间自相关性。半变异函数恰恰可以揭示其在持续空间中的相关性关系。通过半变异函数模拟的数值如表2所示。

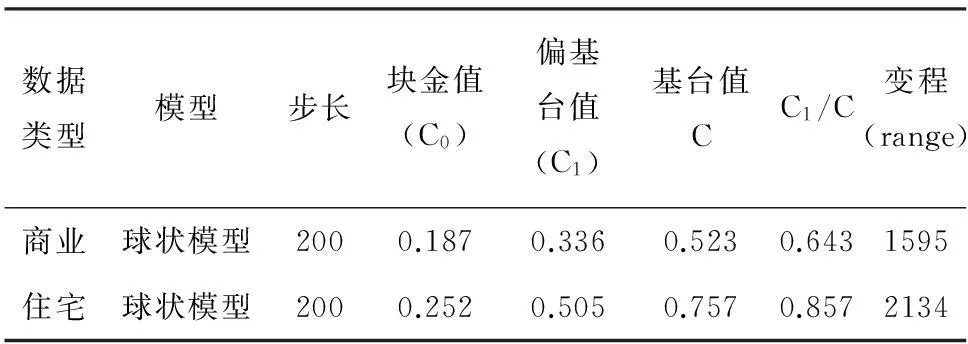
表2:基于球状模型的半变异函数模型参数

表2中基于球状模型模拟的商业和住宅地价的空间变化，反映了半变异函数与距离之间的变化关系。最合研究区的实际情况。块金值C0 住宅地价的值要高于商业地价的值，说明住宅地价对距离的影响更加敏感。同样，基台值C值也是住宅高于商业，与之前分析的住宅Moran’sI指数远大于商业值。C1/C所占的比重都较大，反映了免渡河镇住宅和商业的空间相关性都较为明显，与全局相关性得到的结果相一致。商业地价的变程a为1595m，与Moran’sI指数得到的范围基本一致，而住宅地价变程a达到了2134m，与全局的Moran’sI指数得到的范围值相差较大，考虑到住宅区的分布围绕着城市商业中心而扩散，所以半变异函数下的变程range有一段距离的延伸。而基于全局空间自相关的Moran’sI则更为可靠，所以将商业和住宅的阈值范围设置为1700m较为可靠。住宅区沿街分布的特点受半变异函数影响较大。

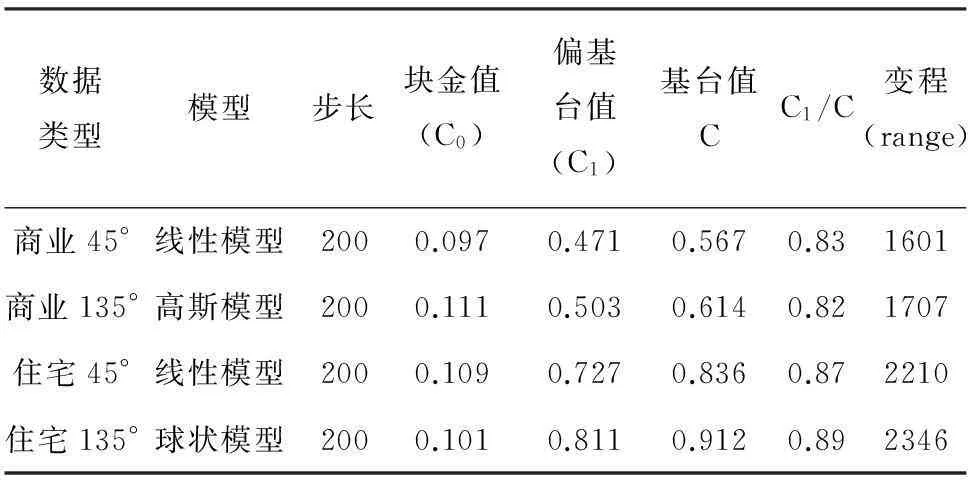
表3:各向异性半变异函数参数

因为免渡河镇建城方向的地理原因，本文选取了45°和135°两个方向作为研究方向，如表3，其空间自相关程度高，但各个方向的空间相关性不尽相同。商业东北—西南的方向上，地价模型成线性增长，而在西北-东南方向上商业地价的增长趋势符合高斯增长模型，且主要是沿街分布的特点。住宅地价在东北—西南方向上符合线性模型的增长趋势，而在西北-东南方向上符合球状模型的增长趋势，其随机性较大，这与免渡河实际状况相吻合，与西北方向矿区的发展和火车站在东南方向有关，住房的选择往往与经济、人口紧密相连。

3Kriging插值法模拟地价空间分布

GIS空间分析也称空间数据分析，是基于地理对象空间布局的地理数据分析技术，空间分析也可以看作是一个空间知识发现和挖掘的过程。[17]插值分析是空间分析的重要部分，其主体思想是对已知样点数据拟合一个空间结构模型进行结构量化分析，从而对某一区域未知点进行预测。[18]Kriging插值法核心是求出最优、线性、内插估计值，突破了经典统计学的限制，综合的考虑了变量的结构性和随机性[19]。

本文运用ArcGIS分析地价的空间变化，首先给空间分布数据地价样点进行投影转换，投影坐标系统选用与二调库一致的(Xian_1980)坐标系。得到研究区的空间插值图，进而预估商业和住宅的地价，并结合免渡河镇的二调图分析其地价分布规律。

如图3所示运用Kriging插值法对地价的空间分布及格局进行研究得到以下规律。

(1)由图3看出，免渡河镇商业一级地482元/m2以上的商业集聚区主要集中在城镇中心偏向西北的方向。而住宅一级地223元/m2以上的住房区主要集中在中央大街与四道街的交汇处，以此为中心，住房价格向四周住房价格逐渐降低。

(2)商业地价在其中心四道街向北一侧向外扩展成“钟形”，商业地价在317-482元/m2的区域主要集中在四道街和五道街形成的包围地带。住宅地价由最高的区域向周边扩散，并形成同心圆结构。161-223元/m2之间的地价区域主要集中在三道街、四道街、五道街和六道街构成的同心圆结构之内。

(3)免渡河的商业区西北方向较为发达，并呈“钟形”结构向东南方向递减，而地价317元/ m2以下的区域则呈圈层结构由城镇中心向郊区扩展。对于住宅区的选择人们往往更倾向于城镇的中心，因为城镇中心距离学校、医院、超市这些人们经常活动的场所更为便捷。

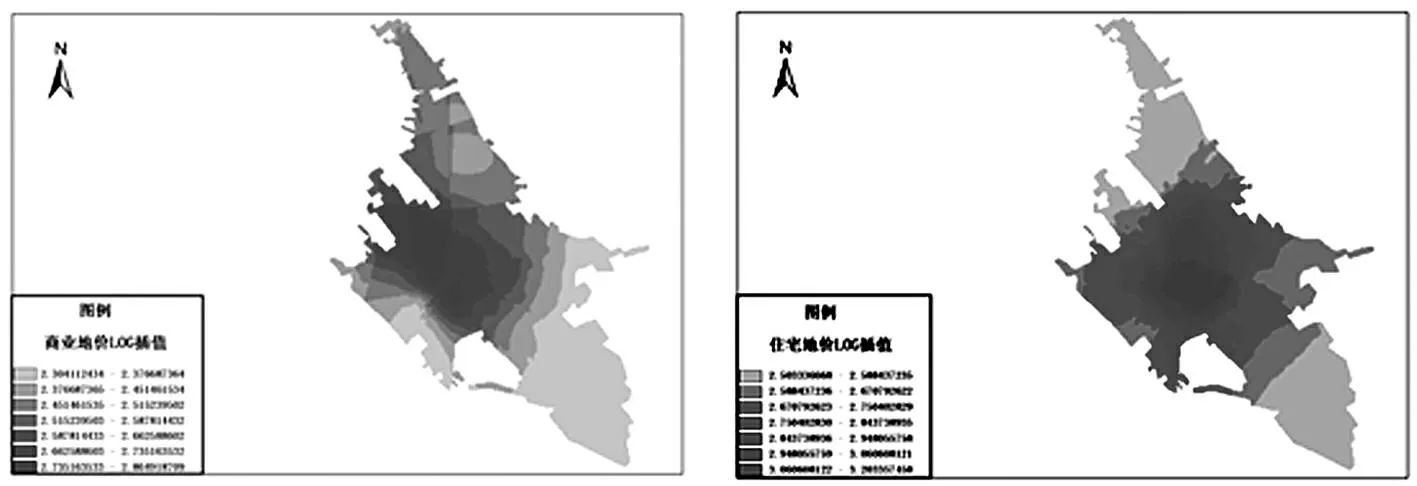
图3:商业和住宅的Kriging插值

4结论与讨论

本文在分析地价空间格局与分布的过程中，运用空间自相关与Kriging插值法两种方法对免渡河镇的地价结构进行了剖析，如空间自相关中的全局自相关反映了地价观测值对整体地区地价的空间格局与集聚规模的变化，从整体上体现地价的空间自相关程度。局域自相关可以探知不同水平、不同区域的空间自相关性和空间异质性。而基于地统计法的半变异函数，揭示了整个空间持续尺度上的变异格局。而在变异函数和相关分析的结果表明区域化变量存在空间相关性，则可以运用Kriging插值法对城镇空间未抽样点或未抽样区域进行估值。以更好的分析城镇地价的空间分布格局。本文结合上述方法对免渡河镇的空间分布格局进行了研究，得到以下结论：

(1)对空间权重矩阵的选择在本研究中显的异常的重要，无论是6个邻居k-nearest的距离权重还是反距离权重都对Moran’sI指数和Getis’G指数的探测具有重要影响。在实际探测的过程中，应该根据地价数据分布特点和研究目的选择合适的空间权重矩阵。在研究全局自相关的过程中，确定了Moran’sI指数所对应的阈值范围，从而为进一步分析地价的空间自相关程度提供了科学依据，而Getis’G指数的确定反映了地价的空间集聚程度，是一种在数字环境下空间相关的衡量尺度。[20]半变异函数主要在如何探测连续空间上的空间相关性和空间异质性上为本研究提供了有力的依据。地价研究需要利用已测样点对未测样点及区域产生预估值，Kriging插值法对地价研究是一个有力的补充。

(2)在探测地价自相关阈值范围时，1700m是反映住宅和商业地价是否具有空间正相关的重要的指标，小于此阈值范围则地价表现为高集聚度，大于此阈值范围地价表现为低值集聚度，地价的自相关程度及Moran’sI指数呈反变动趋势。在西北-东南方向地价的空间自相关范围要大于东北—西南方向，且随机性较强，如商业地价在此方向的的自相关变化程度较大。在全局自相关成高度正相关且局域自相关程度呈高度集聚状态时，住宅和商业分布的区域也不尽相同，住宅主要分布在城镇地理位置的最中心，而商业则要偏向于城镇中心的西北方向一侧。在分析全局呈正相关的地方，局域也表现为高集聚性，但部分区域出现了空间异质性。

本文研究的是小城镇的地价的空间分布格局，所以在研究地价时应该充分考虑空间相互作用的复杂性，选择最合适的权重矩阵进行空间自相关分析。且与大城市相比，小城镇地价的空间异质性不如大城市那么明显，这与小城镇的繁华地段高度集中相关，相对小城镇，大城市那样繁华地段相对分散，局部空间异质性明显。局部Moran’sI指数和局部 Getis’G指数探测空间聚集的能力有显著的差异，但本文在研究时没有对两种指数的差异来源及其变化特征作深入的分析。尤其是对于地价空间的全局空间自相关与局域空间自相关变化机制的内在原因没有做进一步的分析。

〔参考文献〕

[1]Tobler， W. R.. A Computer Movie Simulating Urban Growth inthe Detroit Region[J]. Economic Geography， 1970， 46(2)： 234-240.

[2]李玲，谷树忠，胡克林. 都市地价空间分析方法及其应用[J]. 资源科学，2003， 25(4)： 85-92.

[3]汪应宏，张绍良，郭达志等. 城市地价与房租的空间变异分析以蚌埠市为例[J]. 中国矿业大学学报， 2005， 34(5)： 673-678.

[4]王霞， 朱道林. 地统计学在都市房价空间分布规律研究中的应用 以北京市为例[J].中国软科学， 2004， (8)： 152-156.

[5]任辉， 吴群. 基于 ESDA的城市住宅地价时空分异研究 以南京市为例[J].经济地理， 2011， 31(5)： 760-765.

[6]李玲， 朱道林， 胡克林.北京市城区住宅地价的时空变化规律[J].经济地理， 2011， 31(4)： 655-659.

[7]张洪， 金洁. 城市地价空间的计量经济分析-以昆明市为例[J].资源科学， 2007， 29(7)： 25-32.

[8]张丽芳， 濮励杰， 张静， 等. 基于 Hedonic 模型的城市地价空间结构分析 以湖南省娄底市为例[J]. 经济地理， 2009， 29(9)：1 475-1 480.

[9]吕萍， 甄辉.基于GWR模型的北京市住宅用地价格影响因素及其空间规律研究[J].经济地理， 2010， 30(3)： 472-478.

[10]焦利民，刘耀林，刘艳芳. 区域城镇基准地价水平的空间自相关格局分析[J].武汉大学学报，2009，34(7)：873-877.

[11]蒋芳，朱道林. 基于GIS的地价空间分布规律研究-以北京市住宅地价为例[J].经济地理，2005,25(2):199-202.

[12]马敏蕾，吕斌，冯长春. 基于GIS基础上的北京住房价格空间格局研究[J].资源产业经济，2008，(1)：26-28.

[13]公云龙，张绍良，章兰兰. 城市地价空间自相关分析 以宿州市为例[J]. 经济地理，2011,31(11):1906-1911.

[14]魏晓峰，吴建平，基于ArcGIS的空间自相关分析模块的开发与应用[J].测绘与空间地理信息，2005，28(6)：77-80.

[15]梅志雄，黄亮，房地产价格分布的空间自相关分析-以东莞市为例[J].2008，22(2)：49-54.

[16]徐建华. 现代地理学中的数学方法[M ]. 北京:高等教育出版社 ,2004: 115 - 121.

[17]陈思源,曲福田,倪绍祥,刘友兆, GIS空间分析支持下的城市地价分布研究-以江苏省镇江市为例[J].2005,28(3)119-122.

[18]Benecala K E, Seinfeld J H. On Frequency Distributions of Air Pollution Concentrations [J]. Atmospheric Environments,1976,10:841-850.

[19]BergerA, Melice JL, Demuth C L.Statistical Distribution of Daily and High Atmospheric SO2concentrations [J].Atmospheric Enivornments,1982,16:2863-2877.

[20]Arthur Getis ,J. K. Ord. The Analysis of Spatial Association by Use of Distance Statistics[J].Geographical Analysis,1992,24(3):189-206.

Study on the Spatial Distribution Pattern of Urban Land Price

——A Case Study of Mian DuHe

HU Jun-de1,LI Bai-sui1,ZHANG ting2,GU Jun-jie1

(1.College of Geographical Science,Inner Mongolia Normal University,Hohhot 010022

2.College of Life Science,Inner Mongolia University,Hohhot 010021)

Abstract:The data in this article derived from the urban of Mian DuHe land update and land gradation in 2012. Based on Spatial autocorrelation statistics and Geostatistical theory and methods to explore the distribution pattern of urban land price, Further reveals the spatial characteristics and distribution law of spatial agglomeration. Using global and local spatial statistics for autocorrelation in the index of Moran’ I and Getis’G with the half variation function of geostatistical fora comprehensive analysis of uban of Mian DuHe commercial and residential prices from General to local characteristics the spatial distribution and Anisotropic. Combined with the Kriging interpolation method and its analysis, And using spherical model curves obtained: the land prices in the range of 1700 meters were positively correlated and high aggregation, As the distance increases, its premium autocorrelation gradually weakened, the Spatial autocorrelation of the land in every direction are not the same size, and in some regions there is heterogeneity. In Northwest-Southeast direction premium range of Spatial autocorrelation than as a northeast-southwest direction, and randomness is strong, such as autocorrelation of commercial land in the direction of change is quite large.

Key words:Urban Land price;Spatial autocorrelation;Semi-Variance function;Kriging interpolation;Anisotropic

中图分类号：F301.2

文献标识码：A

文章编号：1004-1869(2015)01-0030-07

作者简介：胡君德(1989-),硕士研究生，研究方向:城市地理与地理信息系统。

收稿日期：2014-09-24