关于递推数列的研究



关于递推数列的研究

王 建 莉

(包头师范学院 数学科学学院，内蒙古 包头 014030)

摘要：数列问题是各种数学问题中的难点之一，而求递推数列通项的问题更是倍受青睐。这类问题一般都是利用“化归”的思想来解决，其技巧性强，学生很难掌握解决此类问题的通性通法。本文总结归纳各种递推数列的类型加以研究，运用特征根法、待定系数法、倒数法、累加法、累乘法、构造等差等比法、迭代法、对数法等一般研究方法求解递推数列通项。

关键词：数列类型；递推数列；通项；递推式

1一阶线性

1.1类型一：an+1=an+f(n)

1.1.1累加法

an=(an-an-1)+(an-1-an-2)+(an-2-an-3)+…+(a2-a1)+a1

=f(n-1)+f(n-2)+f(n-3)+…+f(1)+a1

将上式相加得：

2二阶线性

2.1类型一：an+1=an*f(n)

2.1.1累乘法

an=an-1·f(n-1)，an-1=an-2·f(n-2)，an-2=an-3·f(n-3)

…

a3=a2·f(2)

a2=a1·f(1)

以上各式子相乘得：

=f(n-1)·f(n-2)·f(n-3)·…·f(1)·a1

解：由已知得当n≥2时，有

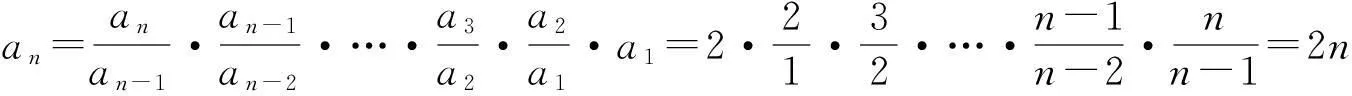
又a1=2

∴an=2n(n∈N*).

2.2类型二：an+1=can+d(c≠0,c≠1,c,d为常数)

2.2.1待定系数法

已知an=can-1+d(c≠0,c≠1,c,d为常数)，设an-r=c(an-1-r),则an=can-1+r(1-c)

2.2.2下坐标变换法

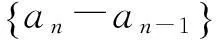
解：方法1：待定系数法

由题设得：an+1+1=2(an-1+1)

故bn=2·2n-1=2n，

∴an=bn-1=2n-1(n∈N*)

方法2：下坐标变换法

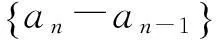
2.3.1对数变换法

lgan+1=lgp+qlgan

令xn=lgan则转化为类型三.

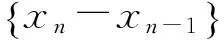
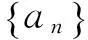
∴lgan=2n-1·lg3

∴an=32n-1

3一阶分式

3.1.1构造法

3.1.2不动点法

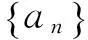
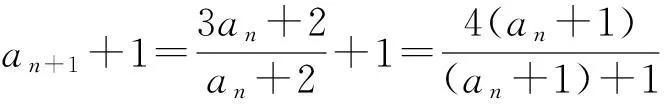
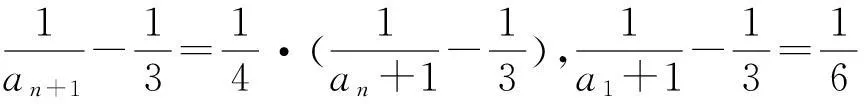
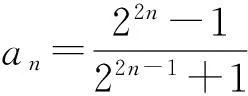
3.2.1倒数法

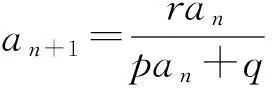
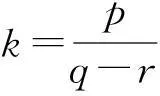
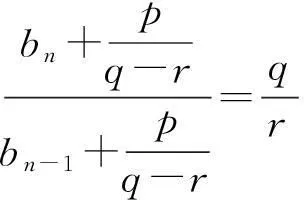
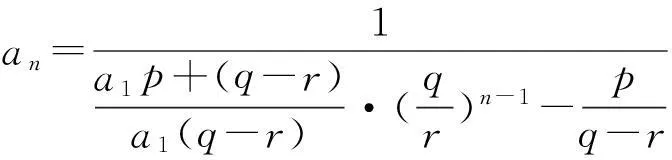
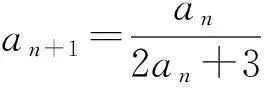
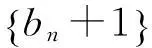
∴bn+1=2·3n-1,

递推数列是指数列的任意连续若干项所满足的关系式(比较常见的通常是给出数列中的相邻两项间的关系)，由递推公式和相应的前若干项可以确定一个数列。本文总结归纳各种递推数列的类型加以研究。对递推数列的深入研究，有助于锤炼思维、提高数学素养，同时也能培养我们分析问题、解决问题的能力以及创新意识。本文尚不够完善，在具体应用上不能很好的体现出来，如利用数列解决生活中实际的问题以及如何应用等问题亟待研究，敬请读者提出宝贵意见。

〔参考文献〕

[1]苏勇. 求递推数列通项公式的专题研究[J].数学教学通讯,2007,(5) .

[2]王红权,姜红. 求数列通项公式的十种常用方法[J].中学生天地(C版),2007,(9) .

[3]王新宏. 递推数列常见形式[J].中学生数理化(高考版),2009,(2) .

[4]熊卫. 递推数列求通项公式[J].科学咨询(教育科研),2009,(11) .

[5]马永传. 递推数列通项公式求法及技巧[J].六安师专学报,1999,(2) .

[6]孔令霞. 递推数列通项公式求法探讨[J].中学数学教学参考,2004,(8) .

Study on Recurrence Sequence

WANG Jian-li

(Faculty of Mathematics,Baotou Teachers College,Baotou 014030)

Abstract:Series of mathematical problems in question is one of the difficulties, the series has been seeking general term recurrence formula is the acclaimed issue. Such problems are generally using the "return of" thinking to solve, their skills strong students to solve such problems is difficult to grasp the connection of common law. This article summarizes the various types of recurrence sequences to study. Using eigenvalue method of undetermined coefficients method, inverse method, cumulative method, tired, multiplication, arithmetic geometric construction method, iterative method, the number of law on the general methods for solving linear recurrence sequence and non-homogeneous line of recurrence sequence entry.

Key words:sequence type; homogeneous or non-linear recursive sequence; general term; recursive

中图分类号：O173

文献标识码：A

文章编号：1004-1869(2015)01-0015-05

作者简介：王建莉(1974-)，女，内蒙古包头人，实验师，研究方向：数学分析。

收稿日期：2014-10-24