用泰勒级数计算连续随机变量的均值和方差



用泰勒级数计算连续随机变量的均值和方差

宋 志 平

(包头师范学院 数学科学学院，内蒙古 包头014030)

摘要：本文给出了利用泰勒级数计算连续型随机变量函数的均值和方差近似解的方法。

关键词：泰勒级数；随机变量；均值；方差

1引言与预备知识

随机变量的均值反应的是随机变量取值的平均水平，而方差则是反应随机变量取值在其平均值附近的离散程度。现代实际生活中，越来越多的决策需要应用均值与方差的思想来对事件发生大小的可能性进行评估，通过计算和分析可以比较科学地得出各个方案的预期效果及出现偏差的大小，从而为我们决定要选择的最佳方案。对于随机变量函数的均值和方差在实际中的应用就更为广泛。

一般“概率统计”教材中关于连续型随机变量连续函数的均值和方差的计算都是以积分形式给出的，计算非常复杂。泰勒级数是数学分析中常用的简化函数关系的工具，应用非常广泛。本文将借助泰勒级数给出计算连续型随机变量函数的均值和方差近似解的方法。

2随机变量函数的均值和方差

2.1随机变量的均值与方差

2.2随机变量函数的均值、方差

一般情况下，随机变量函数的均值和方差的计算应用如下定理，

可知Y=g(x)的概率密度为

其中(α，β)是g的值域，h(y)是g(x)的反函数。于是，

同样，可计算随机变量函数Y的方差

证明略。

此定理可推广到多维随机变量函数的情况。例如：设Z=g(x,y)是随机变量X、Y的连续函数，若二维连续型随机变量(X,Y)的概率密度为 f(x,y)，则

这里要求右边的积分绝对收敛。

3问题的产生

从该定理可知，计算函数的均值和方差需要事先已知自变量X的概率密度函数，而此时如果随机变量的函数比较复杂，往往不能简单地把函数代入积分式而得出答案。在客观实际中，经常遇到自变量X 的概率密度函数未知而其均值及方差已知的情形，如果再利用上述定理计算随机变量函数的均值和方差就相当的困难。而在数理统计中，总体的分布往往是未知的或者是含有未知参数的，但我们可以根据抽取的样本观测值来估计其均值和方差。如下：

设E(X)=μ，D(X)=σ2，样本观测值为X1,X2,…,Xn，则有：

这样，自然会提出问题：在已知自变量的均值及方差的条件下，能否求出函数的均值和方差呢？

4利用泰勒级数计算函数的均值和方差

4.1泰勒级数

如果函数f(x)在点x=x0处存在直至n+1阶的连续导数，则

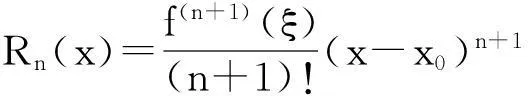
如果在(*)中抹去余项Rn(x)，那么f在x0附近可用(*)式右边的多项式来近似代替，如果函数f在x=x0处存在任意阶的导数，我们称形式为：

的级数为函数 f 在点x0的泰勒级数。

4.2一维随机变量函数的均值和方差

设一维随机变量X的均值E(X)=μ，方差D(X)=σ2。Y=f(X)是连续函数。

将函数Y=f(X)在x=μ 处展开为二阶泰勒级数：

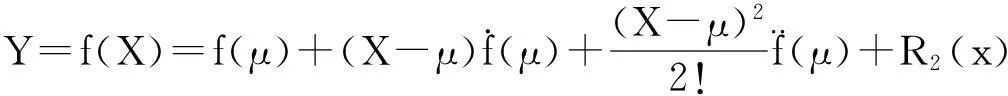
其中R2(x)为二阶泰勒级数的余项。两端取均值，并结合均值的性质，

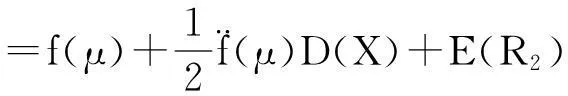
在这里忽略E(R2)，则得：

(1)

得：E(Y)≈f(μ)

同理：将函数Y=f(X)在x=μ 处展开为一阶泰勒级数：

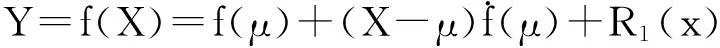
其中R1(x)为一阶泰勒级数的余项。两端取方差，并结合方差的性质，则：

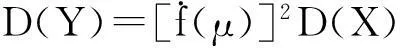
(2)

在实际问题中应用公式(1)、(2)，可以快速地计算出随机变量函数的均值和方差的近似解。

例1：已知：X~N(0,1) ， Y=f(X)=sin2x ，求随机变量函数Y的E(Y)和D(Y)。

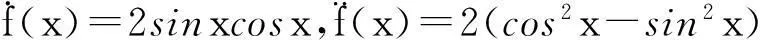
E(Y)≈1，D(Y)≈0。

此公式在实际中应用更为方便。

例2：已知某零件断面半径 r 的均值为μr=10mm，标准差为σr=0.5mm。求断面面积A的均值及标准差。

根据(1)式，可知：

且根据(2)式，可知：

得：σA=√D(A)=31.4 (mm2)。

所以，断面面积A的均值为314.79mm2，标准差为31.4mm2。

4.3多维随机变量函数的均值和方差

设n维随机变量X1,X2,…,Xn的均值E(Xi)=μi，方差D(Xi)=σi2(i=1,2,…,n)。Y=f(X1,X2,…,Xn)是连续函数且具有二阶连续偏导数。 将函数Y=f(X1,X2,…,Xn)在X1=μ1,X2=μ2,…,Xn=μn，处展开为n元函数的二阶泰勒级数：

其中R2(X1,X2,…,Xn)是二阶泰勒级数的余项。

如果X1,X2,…,Xn两两相互独立，忽略余项R2，两边取均值，得Y的均值

(3)

若各D(Xi)的值很小，则

E(Y)≈f(μ1,μ2,…,μn)

(4)

同样，将函数Y=f(X1,X2,…,Xn)在X1=μ1,X2=μ2,…,Xn=μn，处展开为n元函数的一阶泰勒级数：

Y=f(X1,X2,…,Xn)

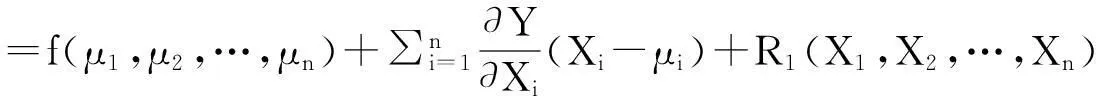
其中R1(X1,X2,…,Xn)是一阶泰勒级数的余项。

如果X1,X2,…,Xn两两相互独立，忽略余项R1，两边取方差，得Y的方差

(5)

例3、 设随机变量X和Y都服从正态分布，Z=XeY是X和Y的连续函数。已知μX=5.420，μY=-0.254，且σX=0.06，σY=0.01。求Z的均值E(Z)和方差D(Z)。

分析：如果直接利用随机变量函数的均值和方差公式来计算E(Z)和D(Z)，将要计算以下两个复杂积分：

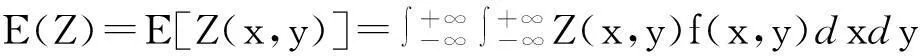
由(3)式得：

=e2yσX2+x2e2y·σY2=e2μY·σX2+μX2e2μY·σY2= 0.0039。

则得D(Y)=σY2

则标准差为：

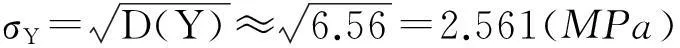
所以，应力的均值为20MPa，标准差为2.561MPa。

5结论

通过以上的论述和实例论证，可以看出：将随机变量的函数在其均值处用泰勒级数展开，略去高次项后，可以计算出随机变量函数的均值和方差。这种计算方法将随机变量函数的均值和方差的复杂积分运算巧妙地转化为求导运算，给出了均值和方差的近似计算公式，使均值和方差的计算变得简单易行，给实际中更好地应用均值和方差带来很大方便。

该近似计算的方法，有一定的误差。其误差大小要由随机变量函数的函数关系而定。对于函数关系为线性函数和二次函数的，由于其二阶以上各阶导数都为0，故没有舍入误差，近似计算公式与严密计算公式是等价的。对于二次以上的高阶函数，会存在舍入误差，且误差的大小由函数的非线性的强度而定。

〔参考文献〕

[1]沈恒范.概率论与数理统计教程[M].第4版.北京：高等教育出版社.2003.

[2]茆诗松.概率论与数理统计教程[M].北京：高等教育出版社.2005.

[3]浙江大学.盛骤.概率论与数理统计[M].北京：高等教育出版社.2005.

[4]金星.系统可靠性与可用性分析方法[M].北京：国防工业出版社.2007.

[5]同济大学应用数学系.高等数学[M].第5版.下册.北京：高等教育出版社.2006.

[6]华东师范大学数学系.数学分析[M].第3版.下册.北京：高等教育出版社.2001.

Calculate the Mean and the Variance of Continuous Random Variable by Using Taylor`s Series

SONG Zhi-ping

(Faculty of Mathematics,Baotou Teachers College,Baotou 014030)

Abstract:In this article,approximate solutions for the mean and the variance of continuous random variable and complex functions are obtained by using Taylorsseries.

Key words:Taylorsseries;random variable;the mean;the variance

中图分类号：O173

文献标识码：A

文章编号：1004-1869(2015)01-0011-04

作者简介：宋志平(1972-),女，内蒙古包头人，硕士，副教授，研究方向：应用数学。

收稿日期：2014-09-14