“治理能力”的数学模型分析——以二元治理为例

刘益春，严蔚刚

（东北师范大学，吉林 长春130024）

“治理”在党的十八届三中全会公报中出现的频次颇多，“国家治理体系和治理能力”更是在党的文件中第一次出现。国家治理体系和治理能力是一个国家制度及其执行能力的集中体现。可以预见，在中国新一轮全面深化改革的过程中，治理理念的引领具有特别重要的意义。

一个治理体系涉及多元要素，这些多元要素的协调、互动、高效运转是产生体系内生动力、平衡提高治理能力的重要保障。然而，在多元治理体系中最基本的关联是二元治理，二元治理是多元治理的基础，多元治理是二元治理的集成，对二元治理的分析和建模是理解多元治理的关键。因此，本文以二元治理为例，并基于圆锥曲线模型，对“治理能力”做一分析和探讨。

一、治理概述

治理是“后工业社会”的产物，源于拉丁文，原意为控制、引导和操纵，当代治理理论中特别强调其协调和持续互动的基本特征。

从20世纪90年代开始，“治理”就声名鹊起，被广泛地用于经济学、政治学和管理学等各个领域的研究。一些国际组织纷纷发表正式报告，专文阐述“治理”。1992年，世界银行将年度报告定题为“治理与发展”。联合国全球治理委员会1995年发表的专题报告提到，“治理是各种公共的或私人的机构管理其共同事务的诸多方式的总和，是相互冲突的或不同的利益得以调和并且采取联合行动的持续过程。它既包括有权迫使人们服从的正式制度和规则，也包括各种人们同意或以为符合其利益的非正式的制度安排”［1］。随后治理一词逐渐得到世界的广泛认可，世界各领域对治理的研究呈现出蓬勃发展的势头，如哈佛大学肯尼迪政府学院的研究项目“二十一世纪的治理”，美国布鲁金斯研究院也将“政府研究”项目更名为“治理研究”。在中国，党的十八届三中全会明确提出，全面深化改革的总目标是完善和发展中国特色社会主义制度，推进国家治理体系和治理能力现代化，也充分反映了从“管理”国家到“治理”国家思维上的巨大跨越。

从治理诞生始，詹姆斯·罗西瑙（James N.Rosenau）、罗伯特·罗茨（R.rhodes）、库曼（Kooiman）等西方学者就试图对治理做出新的定义［2－4］。我国学者俞可平也对治理有深入的研究，并提出了善治的10个基本要素［5］。尽管对治理的论述颇丰，学界始终未有“治理”的统一界定，但我们仍能看出以下几点共同之处：（1）强调主体的多元化；（2）强调自上而下和自下而上的双向互动；（3）治理的建立不以支配为基础，而以调和为基础；（4）治理不是一套规则条例，也不是一种活动，而是一个过程。所以根据以上分析，我们认为，治理是各种公共的或私人的机构管理其共同事务的诸多方式的总和，是协调各利益相关者的相互关系并且采取联合行动，提高效益的持续互动过程。

治理与统治、管理的主要区别与联系，可以用表1简要表示：

表1 统治、管理和治理的区别

二、二元治理的数学模型分析

随着转型期社会的到来，公共事务涉及的领域日益多元化，种类和形式逐渐多样化，发生的频率、速率和影响程度日益扩大，尝试以数学模型的方式来分析治理，有助于更为理性和直观地呈现治理过程。这里重点探讨的是“治理能力”，即在相对稳定的治理体系的基础上，分析治理主体间以及治理主体与客体间的关系对治理能力的影响。治理能力反映治理体系的先进性、实践性和与时俱进的能力。

（一）研究初衷和基本思路

正如上面提及的，二元治理是多元治理的基础，多元治理可看成是二元治理的多次“耦合”。所以，我们把研究重点放在二元治理上。

在经验中，一个二元治理结构的两个治理主体，如果配合默契，治理能力又强，那么治理效果就好，人心相向，相关资源就能够围绕着治理主体较好地运转；反之，如果配合不好，就会人心向背，资源分散，形成两个“中心”，影响整个治理体系的效能。实际上，这种现实中的经验，可以用数学上的圆锥曲线方程表示。圆锥曲线方程是二元二次方程，通常它有两个焦点（特殊情况下有一个焦点），有一个离心率，曲线的形状会随着焦点的位置和离心率的变化而发生变化，这些都与经验中的二元治理高度契合。深入分析圆锥曲线方程，能够发现其蕴含的更加丰富的治理内涵。这个研究过程遵循的是由经验到理性、由特殊到一般的科学归纳过程。

笔者体会，社会科学与自然科学有共通之处。它们在揭示事物的运动发展规律，寻找丰富多彩的现象背后的稳定联系上获得了一致性。

（二）圆锥曲线方程

圆锥曲线包括圆，椭圆，双曲线，抛物线。其统一定义为：到定点的距离与到定直线的距离的比e是常数的点的轨迹叫做圆锥曲线。常数e称为圆锥曲线的离心率，可看成是圆锥曲线与理想圆的偏离程度。当e＞1时为双曲线，当e＝1时为抛物线，当0＜e＜1时为椭圆，当e＝0时为圆。

圆锥曲线的参数方程为二元二次方程：

F（x，y）＝Ax2＋Bxy＋Cy2＋Dx＋Ey＋F＝0.

如果不考虑圆锥曲线的位置，将其归于同一坐标轴内，圆锥曲线的参数方程可简化为：

F（x，y）＝（e2－1）x2－y2＋2px＝0（e≥0，p为曲线半通径的长，经过焦点且与焦点所在的对称轴垂直的弦叫做通径）［7］。

从圆锥曲线的构成以及性质来看，其蕴含的丰富特质，与治理主体与治理客体之间的关系基本对应。假设圆锥曲线的焦点为治理主体；曲线上的点为治理客体；曲线轨迹就相当于治理主体对治理客体的治理模式；固定常数e（离心率），可视为现行治理偏离“善治”的程度；曲线轨迹闭合时形成的面积为治理效益。

（三）圆锥曲线模型的四种治理形态

当离心率e的值变化时，圆锥曲线分化为圆、椭圆、双曲线和抛物线等不同形态，所对应的治理状况也随之变化。

1.椭圆模式。当o＜e＜1，点的轨迹为椭圆，此时曲线轨迹闭合，形成面积。可视为在二元治理中，现行治理趋向“善治”的程度高，两个治理主体（两个焦点）在治理中保持一定的距离，各就其位，相互呼应，治理处于良好状态，形成治理效益。

椭圆的两个焦点呈现密切的正联系，从一个焦点出发的直线经椭圆折射后，经过另一个焦点。可视为从治理主体发出的信息经治理客体后会呈现到另一个治理主体，两个治理主体会因此完成互动。

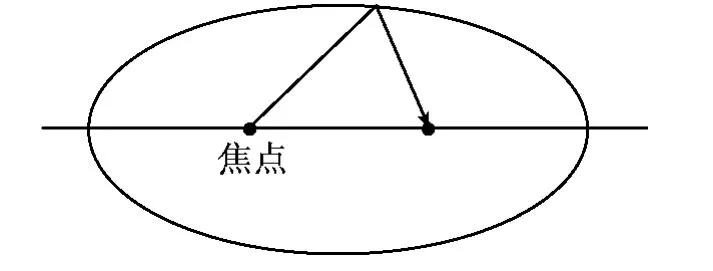
图1 椭圆模式

2.双曲线模式。当e＞1，点的轨迹为双曲线。此时圆锥曲线的两个焦点分而立之，曲线的轨迹一分为二，变成了两条互相分离的轨迹，点的轨迹未形成闭合空间，面积不存在。可视为两个治理主体间保持较远距离，治理偏离“善治”程度趋高，各自为政，资源利用分化，未形成治理效益。

双曲线的两个焦点呈现紧密的负联系，从一个焦点出发的直线经双曲线折射后，其折线的反向延长线经过另一个焦点。可视为从治理主体发出的信息经治理客体后会发散出去，而不会呈现到另一个治理主体，两个治理主体没有互动。

图2 双曲线模式

3.抛物线模式。当离心率e＝1，圆锥曲线的参数方程为F（x，y）＝2px－y2＝0（p为曲线半通径），点的轨迹为抛物线。此时治理偏离“善治”的程度为固定值1，一直处于偏离值固定的特殊状态。圆锥曲线退化成单焦点图形，曲线轨迹成为单一非闭合曲线。在这一状态下，可视为治理中的两个治理主体只存其一，治理仍未形成治理效益。

抛物线的单焦点的特性是：从焦点出发的直线经抛物线折射后，呈平行方向折射出去。可视为从治理主体发出的信息经治理客体后会平行发射，没有交集。

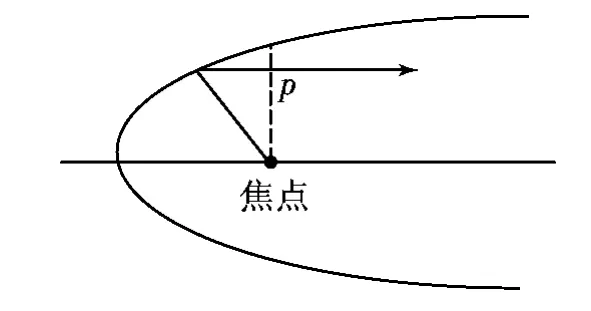
图3 抛物线模式

4.圆模式。当离心率e＝0，圆锥曲线的参数方程为F（x，y）＝x2＋y2－2px＝0，点的轨迹是以（p，0）为圆心，以p为半径的圆。圆锥曲线的两个焦点重合为一，曲线轨迹闭合形成圆形。圆心可视为两个治理主体合为一个点，呈一元形态。

圆心的特性是：从圆心发出的直线经圆折射后，又反射到圆心。可视为从治理主体发出的信息经治理客体后会反馈到自身。

图4 圆模式

总体来看，圆锥曲线的四种模式表达了治理的四种不同情形。在二元治理的框架下，经过综合各方面因素进行最终的模型筛选，结合现实实践，椭圆模式是契合多元治理和善治的一种模型。因此，可确定以椭圆模式作为模型，对实现“善治”进行进一步分析。

（四）椭圆模式的具体分析

假设在椭圆中，椭圆的离心率e＝c／a，两个焦点的距离为2c，椭圆上任意点到两个焦点的距离和为2a，此时，椭圆的参数方程可简化为F（x，y）＝（c2／a2－1）x2－y2＋2a－2c2／a＝0。椭圆的面积S＝π·a·b（π为圆周率）。2c为两个治理主体之间的分离度（分离度越小，治理主体间的配合越默契，反之亦然）。2a为两个治理主体治理总能力，椭圆上的任意点相当于治理客体，椭圆的离心率e为现行治理偏离善治的程度，椭圆的面积S相当于治理体系的治理效益。

评估集是对评估对象风险等级的划分的集合，参照国家标准GB/T 21562对风险等级的划分标准,风险共分为4级，即FR={R1,R2,R3,R4}={可忽略的，容许的，不希望的，不容许的}，对应于证据理论中的识别框架。

1.治理总能力一定，治理主体的治理能力变化情况

假设在椭圆T中，2a和2c的值不变（见图5），P点在椭圆上不断运动，PF1＋PF2＝P′F1＋P′F2＝P″F1＋P″F2＝2a，但无论P点如何运动，PF（即PF1、PF2、P′F1、P′F2、P″F1或P″F2的长度）总在［a－c，a＋c］的区间范围内变化（见图6）。也就是说，在善治的视域下，对于治理客体而言，两个治理主体的治理能力应处于一种和谐状态，即在一定范围内处于不断波动的状态，而不会出现一个治理主体的治理能力极强而另一治理主体极弱的情形。

图5 治理能力的变化图

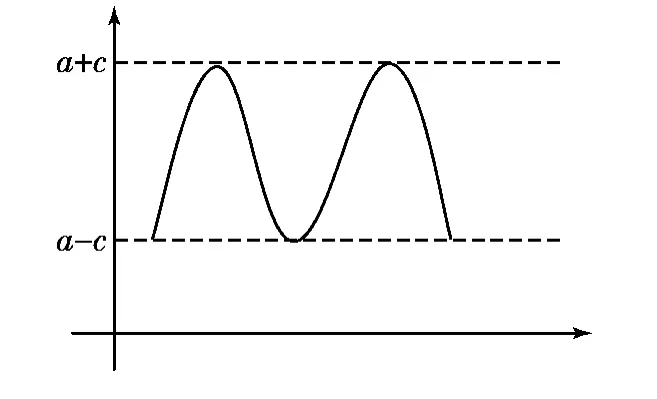
图6 治理能力的范围图

2.治理主体分离度一定，治理总能力的变化情况

为直观起见，下面赋值说明。假设在椭圆T中，2c＝6，2a＝10，圆锥曲线离心率e＝0.6，面积S＝20·π。在椭圆T′中，当P′F1＋P′F2＝2a′＝12（2a′＞2a），那么也就是说，当两个治理主体之间分离度不变，两个治理主体治理总能力增强，那么治理更加契合“善治”（e′＜e），治理效益就相对更高（S′＞S）；假设椭圆T″中，当2c＝6，P″F1＋P″F2＝2a″＝8（2a″＜2a），那么也就是说，当两个治理主体之间的分离度不变，两个治理主体治理总能力减弱，那么治理偏离“善治”程度更高（e″＞e），治理效益相对较差（S″＜S）。（见图7）

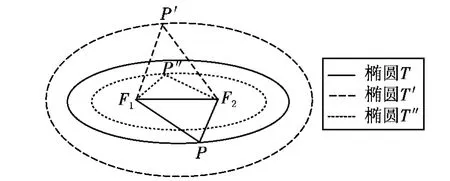
图7 治理主体分离度一定，治理总能力变化与治理效益图

2a与S和2a与e的关系，也就是两个治理主体治理总能力与治理效益的关系和两个治理主体治理总能力与现行治理偏离“善治”程度的关系。假设在椭圆中，2c＝6，以上关系可用函数形式予以反映。且a∈（0，＋∞）。（见图8）而a与e的关系，也就是两个治理主体治理总能力与现行治理偏离善治程度的关系也可用函数形式予以反映。f（a）＝e＝3／a，a＞3且a∈（0，＋∞）（见图9）

图8显示，两个治理主体的治理总能力与治理效益呈正相关，且非简单的线性关系。也就是说，当两个治理主体之间的分离度不变，两个治理主体的治理总能力越强，治理效益就越好。反之，两个治理主体治理总能力越弱，治理效益越差。随着治理总能力的增长变化，治理效益增长变化得更为显著。

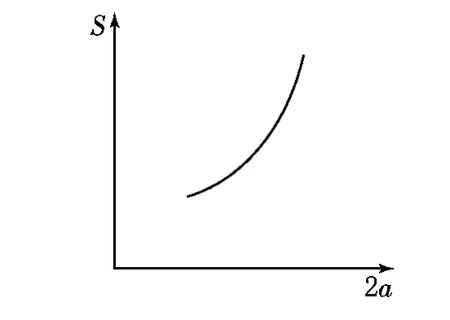
图8 分离度不变，治理总能力与治理效益关系图

图9 分离度不变，治理总能力与离心率关系图

图9显示，两个治理主体的治理总能力与现行治理偏离善治的程度呈负相关且为反比例函数。也就是说，当两个治理主体之间的分离度不变，两个治理主体的治理总能力越强，治理越来越契合“善治”（e越小）；反之，两个治理主体治理总能力越弱，治理越来越偏离“善治”（e越大）。随着治理总能力的衰减变化，离心率衰减变化趋于平缓。

假设在椭圆Q中，2c＝6，2a＝10，圆锥曲线离心率e＝0.6，面积S＝20·π。假设椭圆Q′中，当2a＝10，F′1F′2＝2c′＝8（2c′＞2c），那 么e′＝0.8，S′＝12·π。也就是说，两个治理主体的治理总能力不变，两个治理主体之间的分离度增加，治理更远离“善治”（e′＞e），治理效益就相对较低（S′＜S）；假 设 椭 圆Q″中，当2a＝10，F″1F″2＝2c″＝4（2c″＜2c），那么也就是说，两个治理主体治理总能力不变，两个治理主体之间的分离度更小，发展更契合“善治”（e″＜e），治理效益就相对较好（S″＞S）（见图10）。

图10 治理总能力一定，治理主体分离度变化与治理效益图

2c与S和2c与e的关系，也就是两个治理主体之间的分离度与治理效益的关系和两个治理主体之间的分离度与现行治理偏离“善治”程度的关系。假设在椭圆中，2a＝10，以上关系可用函数形式予以反映。0＜c＜5且a∈（0，＋∞）（见图11）。而c与e的关系，也就是两个治理主体之间配合度与现行治理偏离善治程度的关系也可用函数形式予以反映。f（c）＝e＝c／5，0＜c＜5（见图12）。

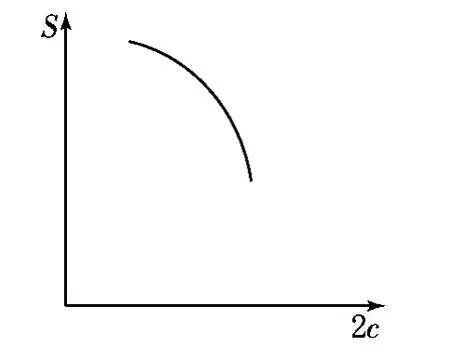
图11 治理总能力不变，分离度与治理效益关系图

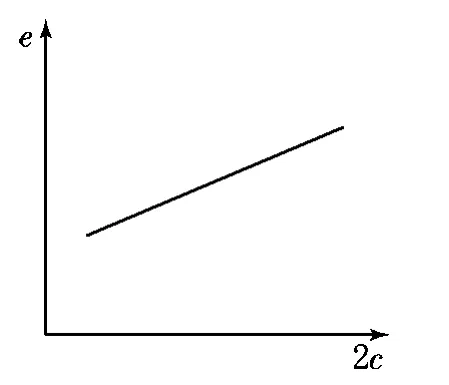
图12 治理总能力不变，分离度与离心率关系图

图11显示，两个治理主体之间分离度与治理效益呈负相关，且非简单的线性关系。也就是说，当两个治理主体的治理总能力不变，两个治理主体之间分离度越小，治理效益就越好。反之，两个治理主体之间分离度越大，治理效益越差。随着分离度的增长变化，治理效益的衰减变化更为显著。

图12显示，两个治理主体治理分离度与现行治理偏离善治的程度呈正相关且为线性关系。也就是说，当两个治理主体治理总能力不变，两个治理主体之间的分离度越大，治理越来越偏离“善治”；反之，两个治理主体之间的分离度越小，治理越来越契合“善治”。

治理能力和分离度是影响两个治理主体治理的重要因素，虽是两个相对独立的方面，但具有很强的互补性。也就是说，当两个治理主体治理能力越高、分离度越小，治理的系统性就越大，治理效益就越好，越接近“善治”。

4.治理客体（资源）自身活力变化情况

受开普勒行星运动规律启发，治理模型还可反映治理客体的活力变化情况。在天体物理学中，太阳系的行星运行轨道近似椭圆，且围绕着太阳运动。行星受到太阳引力不断围绕太阳运行，根据开普勒第二定律，在相等时间内，太阳和运动中的行星的连线所扫过的面积相等。假设在椭圆中，太阳F为治理主体，运动中的行星相当于治理客体（资源）。也就是说，在一定时间内，治理主体和运动中的治理客体（资源）的连线所扫过的面积，即治理效益是相等的。

假设椭圆面上两点围绕焦点运动，则两点在椭圆上扫过的面积相等。如图13 所示，SAB＝SCD。则A点向B点运行的速度大于C点向D点运行的速度。据此，要实现治理效益的最大化，就需要在单位时间内增加治理客体运行的速度，即需要提高资源运行的活力。

图13 治理客体（资源）活力变化图

如图可知，在运动的过程中，某一治理客体与治理主体的距离变化，导致治理客体运行的速度变化，治理客体活力也会随之改变。假设某一治理客体与治理主体的距离为它们之间的科层数，某一治理客体距离治理主体越远，治理主体与治理客体之间科层越多，那么资源运动的速度越慢，资源就越缺乏活力；而某一资源距离治理主体越近，治理主体与资源之间科层越少，那么资源运动的速度越快，资源效益越高。

三、启示与思考

根据以上分析：二元治理模式的治理效益取决于两个治理主体的治理能力、两个治理主体之间的分离度以及治理客体（资源）自身活力。

一是要注重提升治理主体的治理能力，同时加快“有限治理主体”的步伐。为了迎接全球化等趋势以及频发的多样化和大规模的治理危机，建立多元主体共同治理的机制，发挥多元主体的整体力量已是大势所趋，不断提升多元治理主体的治理能力势在必行。欲使多元治理主体主动地参与治理并不断自觉提升其自身的治理能力，就必须强化其主体意识和责任意识。唯有各治理主体对自己的权利和义务有着更深的体认，才会自觉参与治理，主动提升自身的治理能力。不仅如此，在善治的视域下，需要逐步加快“有限治理主体”的步伐。一个良好的多元主体治理结构，要求各治理主体在治理能力上保持一定范围内的均势，否则，治理结构的平衡将被打破。所以，治理主体在保持治理总能力提升的基础上，应限制单个治理主体治理能力的无限制扩张，保持治理主体间的权力平衡，唯有如此，才能逐步推进善治的进程。

二是要注重协调好治理主体之间的关系，增强协同能力。上世纪90年代，美国心理学家在情绪研究中提出了与“智商”（IQ）相对的“情感智慧”的概念，通常称为“情商”（EQ）。情商作为治理主体的重要衡量指标之一，主要指其认识自身的情绪、认知他人的情绪以及人际关系管理等方面的能力。在多元治理中，为确保整体治理效益的最大化，治理主体不仅要具备较强的治理能力，更要增强主体间处理相互关系的“情商”。要在工作开展中加强思想上、情感上的沟通和交流，相互尊重，相互信任，相互“补台”而不“拆台”，合力推进治理。要创建一种共同治理机制，即借助制度化的谈判达成共识，建立互信，以促成个人、组织和系统战略等各个层次上的合作，让多元治理主体的配合成为一个系统，协同前进。比如世界银行在1992年的研究报告《治理与发展》中指出，好的治理的基础在于建立制度化的政府—公众互动平台，增进公众参与［8］。

三是要注重扁平化管理，提升资源“活力”。治理主体的多元容易造成资源利用效率偏低。在传统的管理中，对资源的管理和使用较为繁琐，层级较多，不可避免地使资源配置带有明显的行政化色彩，这种管理方式，不仅惯性地强化了行政权力，而且限制了社会力量参与治理的积极性。因此，应减少治理主体与治理客体之间的层级，实行扁平化管理。即通过减少决策在时间和空间上的延迟过程，将决策权向组织结构的下层转移，让基层单位拥有充分的自主权，并对产生的结果负责，保证上下层能及时有效地进行沟通、对接。如此就会提升资源的活力，让资源高速和谐的运转起来，不断使现行治理趋于善治。

以上是通过圆锥曲线模型的分析，对二元治理进行的初步思考。实际上，圆锥曲线模型也可应用于多元治理的分析。因为二元治理是多元治理的基础，任何一个多元治理都可看成是多个二元治理的“耦合”过程，即一个二元的治理效应可看成一个一元的“耦合治理”，这个“耦合治理”与体系内另外的治理主体又构成了新的二元治理，其治理效应又可看成是一个新的一元耦合治理，以此类推。这与恩格斯所说的历史合力说，即“平行四边形法则”本质上是相通的［9］。所以，圆锥曲线模型可推广至多元治理的分析。当然，治理是一项系统而复杂的工程，上述模型分析仅是初步探索，对这一规律的认识还有待进一步深入。

中国科学院物理研究所孟庆波研究员对本文提出了建设性意见，东北师范大学学校办公室杨朔镔、肖立勋，政策研究室王金龙对此文亦有贡献，特此致谢。

［1］ The UN Commission on Global Governance，Our Global Neighborhood［M］.OxfordUniversityPress，1995：2.

［2］ ［美］詹姆斯·罗西瑙.世界政治中的治理、秩序和变革.张志新，译［M］／／詹姆斯·N·罗西瑙，等.没有政府的治理［C］.张胜军，等，译.南昌：江西人民出版社，2001：55.

［3］ ［英］罗伯特·罗茨.新的治理.木易，编译［M］／／俞可平.治理与善治.北京：社会科学文献出版社，2000：86－106.

［4］ Kooiman，J.Soeial－Political Governance：Overview，Reflection and Design［J］.PublicManagement，1999，1（1）：67－92.

［5］ 俞可平.论国家治理现代化［M］.北京：社会科学文献出版社，2014：27－30.

［6］ 李福华.大学治理与大学管理：概念辨析与边界确定［J］.北京师范大学学报：社会科学版，2008（4）：19－25.

［7］ 李希颜.二次曲线离心率e与曲线形状的关系［J］.数学通报，1981（1）：15－18.

［8］ 钱海梅.关于多元治理主体责任界限模糊性的思考［J］.改革与战略，2007（6）：44－47.

［9］ 马克思恩格斯选集：第4 卷［M］.北京：人民出版社，1995：697.