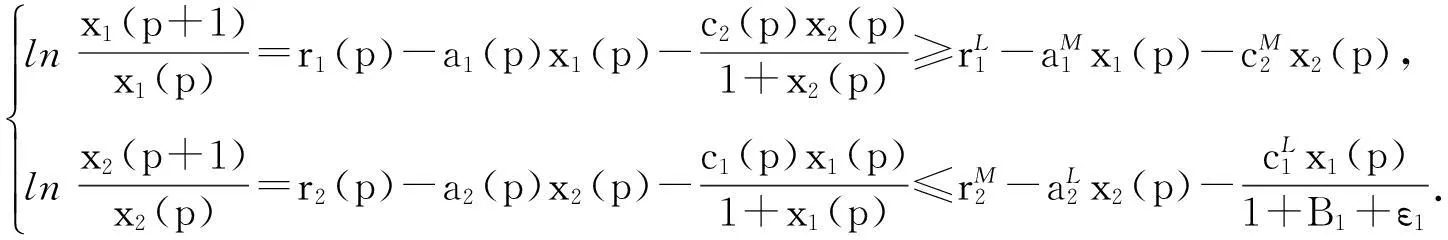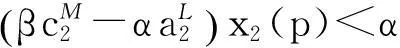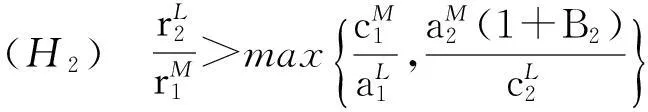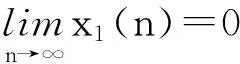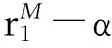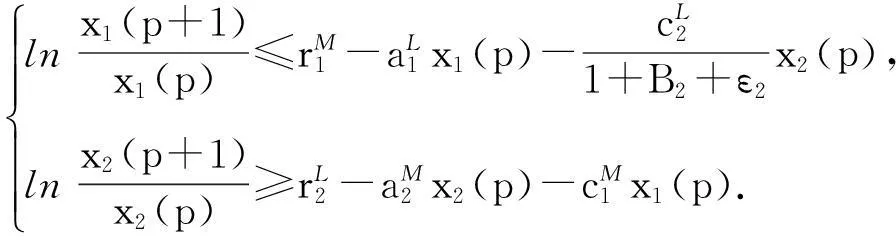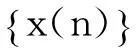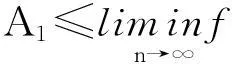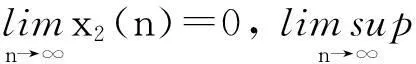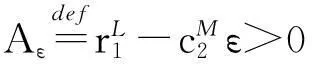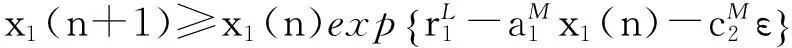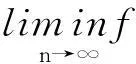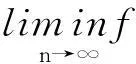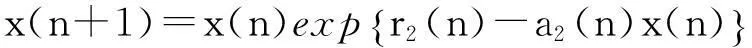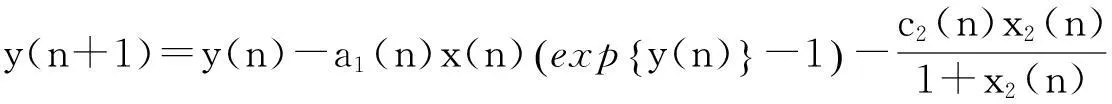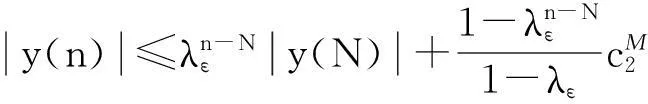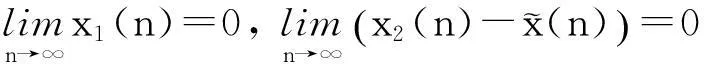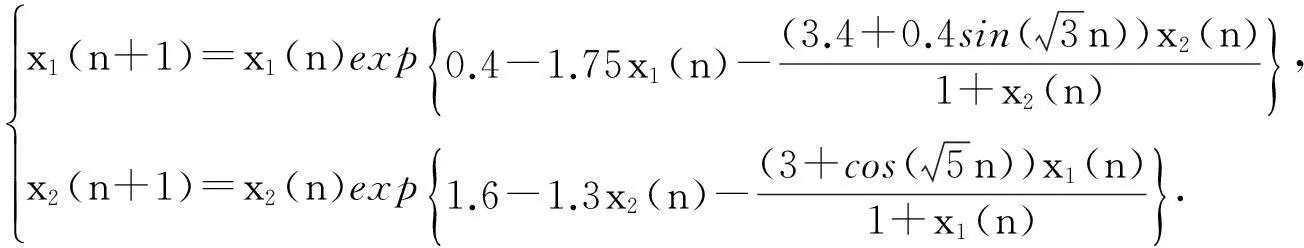一类离散非自治竞争系统的绝灭性和稳定性
余胜斌
( 阳光学院 基础教研部, 福建 福州 350015 )
一类离散非自治竞争系统的绝灭性和稳定性
余胜斌
( 阳光学院 基础教研部, 福建 福州 350015 )
摘要:通过构造适当的Lyapunov绝灭函数,研究了一类离散非自治竞争系统,得到了保证系统中某个种群绝灭和另外一个种群全局吸引的充分性条件,所得的结果补充了前人的工作. 竞争; 绝灭性; 稳定性; 离散; 非自治 O175.14
文献标识码:A
0引言
近年来,如下具有非线性相互抑制项的竞争系统受到学者们的关注[1-6]:
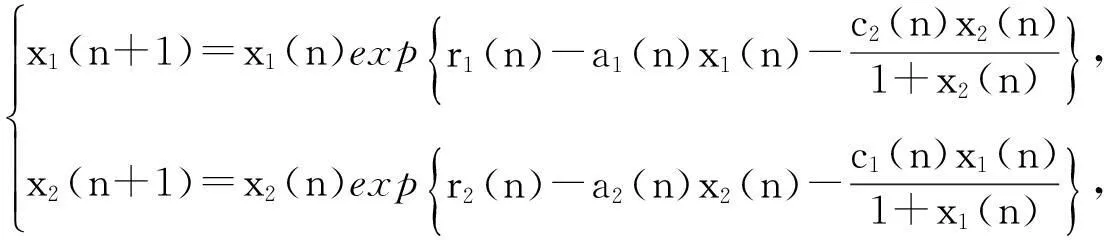
(1)
其中: x1(n)和x2(n)分别表示2个竞争种群在第n代的种群密度, ri(n) (i=1,2)表示2个种群的内禀增长率, ai(n) (i=1,2)为2个种群的种内竞争系数, ci(n) (i=1,2)为2个种群的种间竞争系数.Qin Wenjie等[1]探讨了系统(1)的持久性和全局稳定的周期解的存在性.受文献[1]启发,Wang Qinglong等[2-3]通过定义Lyapunov函数和适当的分析手法,得到了系统(1)相应的离散和连续概周期系统存在唯一全局渐进稳定的正概周期解的充分性判据.考虑到自然界受人类开采等因素的影响,Wang Qinglong等[4]进一步讨论了具反馈控制的系统(1)的动力学行为.笔者在文献[5]中进一步探讨了反馈控制变量对系统(1)持久性的影响,得到了反馈控制变量不会影响系统持久性的结论,从而改进了文献[4]的结果.但是,文献[1-5]均未探讨系统的绝灭性.由于绝灭性是生态系统研究中的一个重要课题,与物种或者自然资源的保护和开发等有直接的关系[6],因此本文就系统(1)的绝灭性进行探讨,类似的工作参见文献[6-9]及其所引文献.


1绝灭性
以下将证明在适当的条件下,种群x2或x1将趋于绝灭.
引理1系统(1)的任一正解(x1(n),x2(n))T均满足:
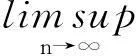
(2)
即系统(1)的任一正解是最终有界的.
证明引理1的证明与文献[7]中引理2.1的证明类似,这里不再给出.
定理1假设如下条件(H1)成立:
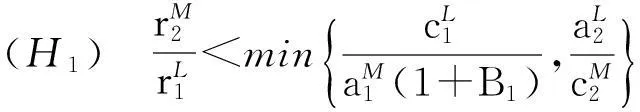

证明由条件(H1)可选取足够小的数ε1>0, 使得

(3)

(4)
对上述ε1, 由引理1可知存在足够大的自然数N>0, 使得当n≥N时,有
xi(n) (5) 对任意的p≥N, 由系统(1)和式(5)可知: (6) 由不等式(4)—(6)可得,对p≥N有 (7) (8) 定理2假设如下条件(H2)成立: 证明由条件(H1)可选取足够小的数ε2>0, 使得 (9) (10) 对任意的p≥N, 由系统(1)和式(5)可知: (11) 由不等式(5)、(10)和(11)可知,当p≥N时,有 (12) 余下的证明与定理1的证明类似,故省略. 2稳定性 以下将讨论在一个种群绝灭的情况下另一个种群的稳定性问题,为此,首先给出几个引理. 引理3假设(H1)成立,则系统(1)的任一正解(x1(n),x2(n))T均满足: 证明由引理1和定理1可知: (13) (14) 由式(13)知,对上述ε>0, 存在足够大的N1>0, 使得对任意的n≥N1, 有x1(n)≤B1+ε, x2(n)≤ε.从而由系统(1)的第1个方程可知 (15) (16) 引理3得证. 引理4假设(H2)成立,则系统(1)的任一正解(x1(n),x2(n))T均满足: 证明类似于引理3的证明可以得到引理4的证明,故省略. 下面考虑如下logistic方程: (17) 这里r1(n)和a1(n)为非负有界序列.由文献[7]中的引理3.2可得: 对如下logistic方程: (18) 与引理5类似的有如下结论: 定理3假设(H2)成立,且如下条件(H3)也成立: 则系统(1)的任一正解(x1(n),x2(n))T和方程(17)的任一正解x(n)有: (19) (20) A1-ε≤x1(n)≤B1+ε, x2(n)≤ε, A1-ε≤x(n)≤B1+ε. (21) (22) 类似地,可以得到如下定理: 定理4假设(H2)成立,且如下条件(H4)也成立: 3应用举例 例1考虑如下系统: (23) 对系统(23)来说,经过验证发现条件(H1)和(H3)成立,从而由定理3可知x2绝灭而x1全局吸引,数值模拟(图1)也支持这一结果. 图1 具初始条件为和的系统(23)的数值模拟 例2考虑如下系统: (24) 对系统(24)来说,经过验证发现条件(H2)和(H4)成立,从而由定理3可知x1绝灭而x2全局吸引,数值模拟(图2)也支持这一结果. 图2 具初始条件为和的系统(24)的数值模拟 参考文献: [1]Qin W J, Liu Z J, Chen Y P. Permanence and global stability of positive periodic solutions of a discrete competitive system[J]. Discrete Dynamics in Nature and Society, 2009(2009):Article ID 830537,13. [2]Wang Q L, Liu Z J. Uniformly asymptotic stability of positive almost periodic solutions for a discrete competitive system[J]. Journal of Applied Mathematics, 2013(2013):Article ID 182158,9. [3]Wang Q L, Liu Z J, Li Z X. Existence and global asymptotic stability of positive almost periodic solutions of a two-species competitive system[J]. International Journal of Biomathematics, 2014,7(4):1450040. [4]Wang Q L, Liu Z J, Li Z X. Positive almost periodic solutions for a discrete competitive system subject to feedback controls[J]. Journal of Applied Mathematics, 2013(2013):Article ID 429163,14. [5]Yu S B. Permanence for a discrete competitive system with feedback controls[J]. Communications in Mathematical Biology and Neuroscience, 2015(2015):Article ID 16. [6]陈凤德,赵亮.一类非自治两种群浮游生物相克模型的绝灭性[J].沈阳大学学报(自然科学版),2014,26(1):1-3. [7]Li Z, Chen F D. Extinction in two dimensional discrete Lotka-Volterra competitive system with the effect of toxic substances[J]. Dynamics of Continuous,Discrete and Impulsive Systems, Series B: Applications & Algorithms, 2008,15(2):165-178. [8]Chen F D, Gong X J, Chen W L. Extinction in two dimensional discrete Lotka-Volterra competitive system with the effect of toxic substances(II)[J]. Dynamics of Continuous, Discrete and Impulsive Systems, Series B: Applications & Algorithms, 2013,20(4): 449-461. [9]Chen L J, Chen F D. Extinction in a discrete Lotka-Volterra competitive system with the effect of toxic substances and feedback controls[J]. International Journal of Biomathematics, 2015,8(1):1550012(13). [10]Chen F D. Permanence for the discrete mutualism model with time delays[J]. Mathematical and Computer Modelling, 2008,47(3):431-435. Extinction and stability in a class of discrete non-autonomous competition system YU Shengbin (DepartmentofBasicTeachingandResearch,YangoCollege,Fuzhou350015,China) Abstract:A class of discrete non-autonomous competitive system of two species is considered. By constructing some suitable Lyapunov type extinction functions, sufficient conditions which guarantee the extinction of species and the stability property of another species are obtain. The results supplement some known results. Keywords:competitive; extinction; stability; discrete; non-autonomous 文章编号:1004-4353(2015)04-0279-06 作者简介:余胜斌(1984—),男,讲师,研究方向为生物数学. 收稿日期:2015-10-28基金项目: 福建省自然科学基金资助项目(2015J01012,2015J01019)