线性回归模型参数的变点检验
刘 宣
( 阳光学院 基础教研部, 福建 福州 350015 )
线性回归模型参数的变点检验
刘宣
( 阳光学院 基础教研部, 福建 福州 350015 )
摘要:线性回归模型随应用环境的改变其模型的参数有可能发生变化,因此有必要对模型的参数进行检验与分析.对于误差项不一定服从正态分布的线性回归模型,通过使用前后样本最小二乘估计量之差的适当权数,获得了变点检验统计量及其渐进分布. 线性回归模型; 变点; 最小二乘估计 O212.1
文献标识码:A
0引言
设线性回归模型:
Y=X β+ε,
(1)
其中X=(1,X1,X2,…,Xp-1)是协变量, Y是响应变量, β=(β0,β1,…,βp-1)T是回归系数.如果有n个观察值(X1,i,X2,i,…,Xp-1,i,Yi),i=1,2,…,n, 则
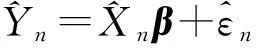
(2)
在实际问题中,模型(2)的线性结构可能不变,但其中的回归参数可能会随着某些因素而发生改变.如果改变,则线性模型(2)可由下列模型代替:

(3)
H0:β0=β2=…=βp-1;

若出现多个变点,可用二分法逐步检验.下面给出变点分析需要的一些假设条件:

1检验过程
假设H0: β=γ,H1: β≠γ.若假设1和2成立,则可分别得参数β的前k个样本和后N-k个样本的最小二乘估计:
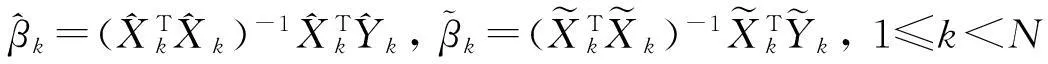
其中


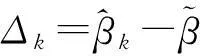
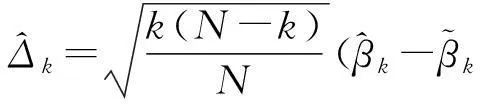

2主要结论及其证明

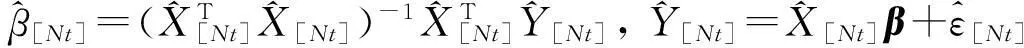

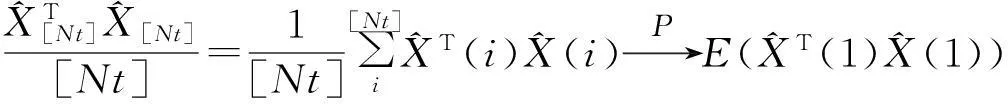

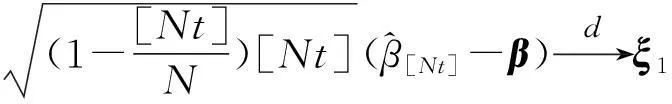

由大数定理和中心极限定理得:


于是,由Slutsky定理有



对于1≤k≤d, 令
B1=(1-θ)2(β-γ)T(β-γ),B2=θ2(β-γ)T(β-γ),
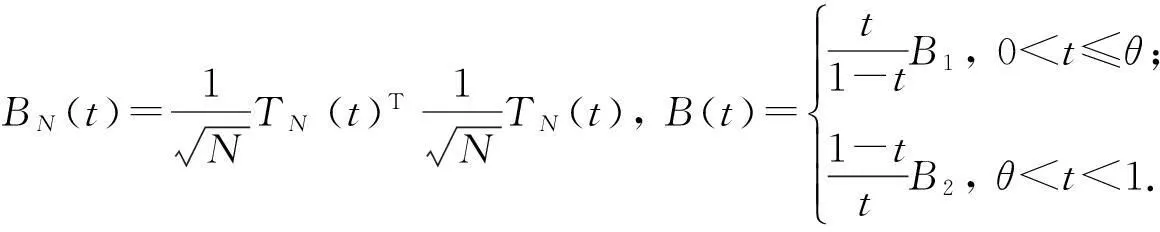

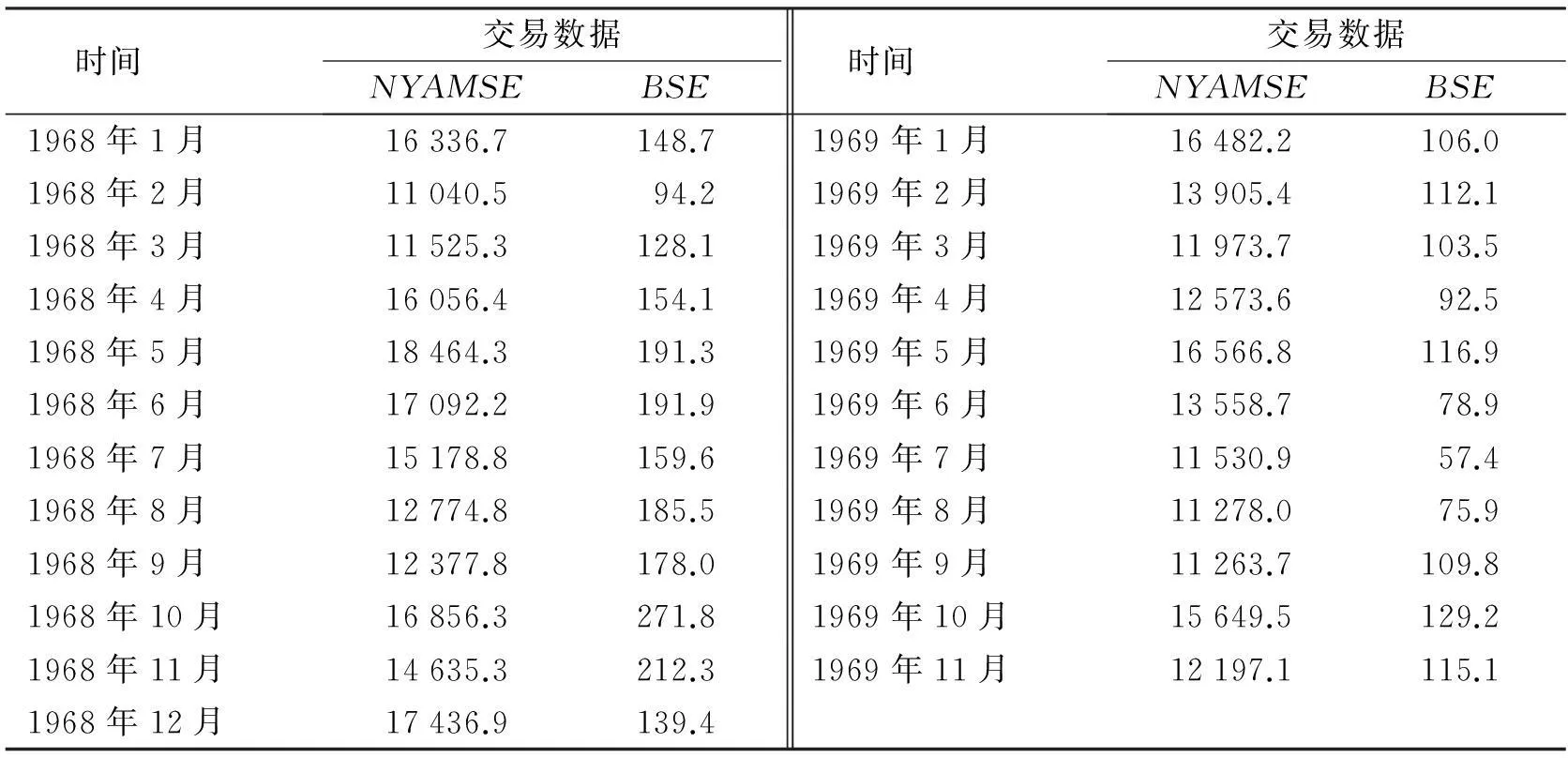
证明若0 注意到: (1-t)-1(θ-t)β+(1-t)-1(1-θ)γ. 所以有 (4) (5) 3实例分析 表1 1968年1月—1969年11月每个月的波士顿股票交易所和纽约证券交易所的交易数据 参考文献: [1]QuandtRE.Theestimationoftheparametersofalinearregressionsystemobeyingtwoseparateregimes[J].JAmerStatistAssoc, 1958,53:873-880. [2]QuandtRE.Testingofthehypothesisthatalinearregressionsystemobeystwoseparateregimes[J].JAmerStatistAssoc, 1960,55:324-330. [3]LiuYukun,ZouChangliang,ZhangRunchu.Empiricallikelihoodratiotestforachange-pointinlinearregressionmodel[J].CommunicationsinStatistics-TheoryandMethods, 2008,37(16):2551-2563. [4]ChenJie.Testingforachangepointinlinearregressionmodels[J].CommunicationsinStatistics-TheoryandMethods, 1998,27(10):2481-2493. [5]HawkinsDL.Au-iapproachtoretrospectivetestingforshiftingparametersinalinearmodel[J].CommunicationsinStatistics-TheoryandMethods, 1989,18(8):3117-3134. [6]FanTsai-Hung,ChangKuo-Ching,LeeChung-Bow.Bayesianestimationofthenumberofchangepointsinsimplelinearregressionmodels[J].CommunicationsinStatistics-TheoryandMethods, 2006,35(4):689-710. [7]CsorgoM,HorvathL.LimitTheoremsinChange-PointAnalysis[M].NewYork:JohnWiley&Sons, 1997. [8]BerkesI,GabrysR,HorvathL,etal.Detectingchangesinthemeanoffunctionalobservations[J].JRStatSocSerB, 2009,70:927-946. [9]HolbertD.ABayesiananalysisofaswitchinglinearmodel[J].JEconometrics, 1982,19:77-87. Testing for chamge-point of parameters in the linear regression model LIU Xuan (DepartmentofBasicTeachingandResearch,YangoCollege,Fuzhou350015,China) Abstract:The parameters of linear regression models may change with the change of the application environment. So it is necessary to test and analyze the parameters of the model. Using appropriate weight difference of the front and back samples least squares estimators of the regression parameters, we obtained an effective test statistics and gradual distribution for linear regression model that error distribution may not satisfy normal distribution. Keywords:linear regression model; change point; least squares estimator 文章编号:1004-4353(2015)04-0295-05 作者简介:刘宣(1982—),男,讲师,研究方向为概率论与数理统计. 收稿日期:2015-10-13
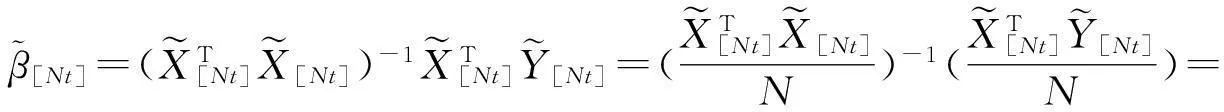


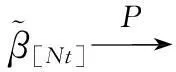
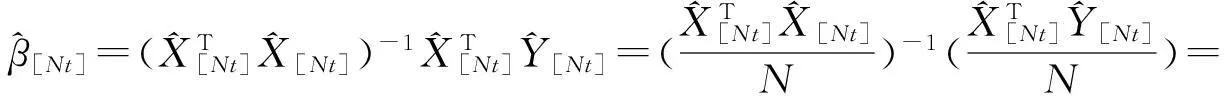
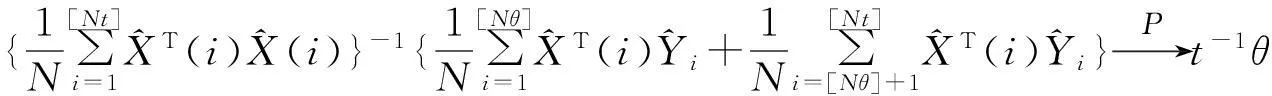

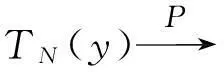

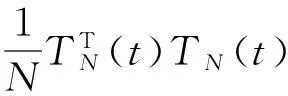
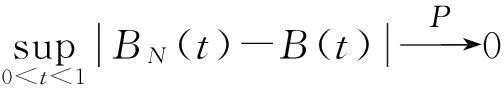


——社会科学教研部

