采用改进的混合遗传算法求解高校排课问题

张赫男，张绍文

北京林业大学 经济管理学院，北京 100083

1 引言

排课问题是一个在教育机构中广泛存在的问题，能否有效地解决排课问题将直接关系到教学质量的好坏。近年来，随着高校的扩招，学生的数量日益增多，并且随着社会的发展，专业和课程的种类也都在与日俱增。在这样的环境下，教师和教室等资源显得愈发紧张。因此，一个有效的课程安排已经成为教师、学生以及学校管理人员的共同诉求。

排课问题是一种多约束和多目标的组合优化问题，它已被证明是一个NP难问题[1-2]。国内外的学者已经提出了一些解决排课问题的方法。早期的解决方法主要有直接启发式方法[3]，图着色法[4-5]，整数线性规划法[6-8]，网络流法[9-10]，这些方法能够解决问题的规模都很有限。随着计算机技术的发展，尤其是20世纪90年代以来，越来越多的智能算法被应用于解决排课问题，如遗传算法[11-13]，模拟退火算法[14]，禁忌搜索算法[15]，以及多种智能算法相结合的混合算法[16-17]。这些算法都能在一定程度上解决排课问题，但也存在着一些不足：（1）考虑的约束条件不够全面，如对合班的情况考虑比较少[18-19]；（2）目标函数仅仅取决于约束条件被违反的次数，并没有考虑到不同课程的重要程度以及不同时间段具有不同的教学效果等[13，18]。本文针对这些不足之处提出了改进的方法。

遗传算法具有自组织、自适应和自学习性，不需要其他的辅助知识，只需要影响搜索方向的目标函数和相适应的适应度函数[20]；遗传算法进行的是全空间的并行搜索，并将搜索重点集中于性能高的部分，从而能够提高效率，而且不容易陷入局部最优[21]。遗传算法采用的是群体并行搜索，局部搜索能力较差；而模拟退火算法采用的是串行优化结构，全局搜索能力较弱。二者的结合能够互相增强和补充进化的能力[21]。因此，本文将遗传算法与模拟退火算法相结合，用以解决高校排课问题。

2 高校排课问题分析及数学建模

2.1 问题描述

排课问题是一种资源分配问题，是要将班级，课程，教师，时间和教室等要素进行合理的安排，在满足各种约束条件的前提下，使目标函数尽量达到最优。不管是学生，教师，还是管理人员，都倾向于同一门课程在同一学期内固定在同一个教室，因此本文没有考虑周次的概念，而是重点研究了课程安排最为密集的一周，若这周的课程可以得到合理的安排，则其他周次的课程安排只须在该周的基础上做一定的删减。

2.2 相关术语

小班：以专业名称、年级和班级编号确定下来的班级，例如“会计10-1”表示会计专业10级1班。

班级：在同一时间同一地点学习同一科目的小班的集合，可以只由一个小班组成，也可以由多个小班组成。

科目：一名固定的教师和一个固定的班级所对应的课程。若存在不同的班级或不同的教师对应名称相同的科目，则在原始数据预处理过程中通过修改科目名称和赋予不同的编号作为区分。一个班级可以对应多门科目，但一门科目只能对应一个班级。

时间段：以每一节课时长45 min为例，在现实的教学中，一般都是2～4节课连在一起进行教学，如上午1～2节，上午1～4节，等等。根据这个特点，将每天的教学时间划分为5个时间段，上午1～2节为第1个时间段，上午3～4节为第2个时间段，以此类推。若是3节课连在一起，如下午2～4节，则等同于下午要占用2个时间段，因为在这种情况下，下午的第1节已无法再安排其他课程。由于晚上一般最多只会安排一个科目，因此把晚上的教学时间记为每天的第5个时间段。

2.3 数据结构和变量

本文对变量的命名采用“属性+类”的方式，变量名中排在后面的单词首字母要大写，以便于阅读。若变量为一个元素，则首字母小写；若变量为一个集合，则首字母大写。如表示教师i的编号的变量命名为idTeacheri，表示班级j要学习课程的编号集合的变量命名为IdSubjectClassj。

原始数据包括以下4个表：

（1）配置表（CONFIG）：每天的时间段数nbPeriodDay=5，每周上课的天数nbDayWeek=5。可以计算出每周的总时间段数nbPeriodWeek=nbPeriodDay×nbDayWeek=25， 每周所有时间段的集合PeriodWeek={1，2，…，nbPeriodWeek}。

（2）教室表（ROOM）：共有nbRoom个教室，教室i对应的编号和容量分别为idRoomi和capacityRoomi。

（3）科目表（SUBJECT）：共有nbSubject门科目，科目i对应的编号、学分和每周的课次分别为idSubjecti，creditSubjecti和nbPeriodSubjecti。

（4）小班表（SMALLCLASS）：共有nbSmallclass个小班，小班i对应的编号和人数分别为idSmallclassi和sizeSmallclassi。

通过Access与Matlab混合编程，生成建模和求解所需要的其他数据，包括以下2个表：

（1）班级表（CLASS）：共有nbClass个班级，班级i对应的编号、包含的小班的编号集合、总人数、科目的编号集合、每周的课次分别为idClassi，IdSmallclassClassi，sizeClassi，IdSubjectClassi和nbPeriodClassi。

（2）教师表（TEACHER）：共有nbTeacher名教师，教师i对应的编号和科目的编号集合分别为idTeacheri和IdSubjectTeacheri。

2.4 硬约束条件

硬约束指的是必须被满足的、符合客观逻辑的约束[22]。本文考虑了4个硬约束条件：

（1）同一时间，同一班级最多只能有一门课程。

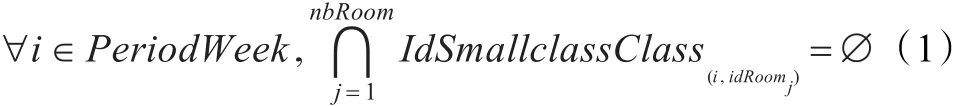
（2）同一时间，同一教师最多只能有一门课程。

（3）同一时间，同一教室最多只能有一门课程。

（4）教室的容量不小于在该教室上课的班级的总人数。

硬约束是否被满足决定了排课方案是否可行。

2.5 软约束条件

软约束指的是在客观上可以被违反，但会影响到教学质量的约束[22]。本文考虑了4个软约束条件：

（1）重要的课程应尽量安排在教学效果更好的时间段。

（2）对于同一个班级的同一门课程，若每周的课次较多，则应尽量避免安排在同一天。

（3）对于每一个班级，要在考虑到课程重要程度的前提下尽量把课程均匀安排在每一天，避免出现某天重要性较高的课程过多或某天重要性较低的课程过少的情况。

（4）尽量实现班级人数与教室容量的匹配，以提高教室的利用率。

2.6 目标函数

目标函数的优劣由软约束的满足情况决定，软约束被满足的情况越好，目标函数越优。本文的目标函数是对各个软约束条件被满足情况的综合评价。

（1）时间段安排效果

对于小班i，找出所有跟该小班有关的科目的学分以及时间段的安排，评价函数如下：

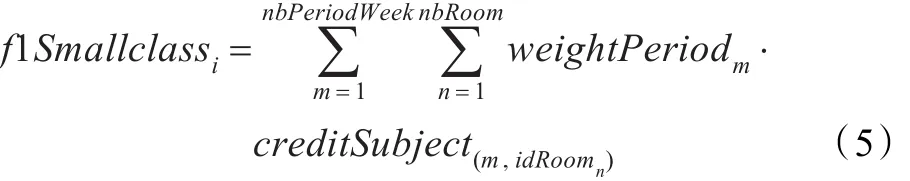
其中weightPeriodm表示第m个时间段的权重值。将每天的第1、3和5个时间段的权重值设置为1，每天的第2和4个时间段的权重值设置为0.5。课程的重要程度直接用学分的大小来衡量。

（2）同一课程应尽量避免安排在同一天

记小班i的课程安排总体效果为f2Smallclassi，初始值为0。对于小班i的科目j，计算该科目每周一共有多少课次。本文一共有3种情况。

①科目j每周只有1课次。则对该科目有f2Smallclassi=f2Smallclassi+2。

②科目j每周共有2课次。分别计算出2个课次对应的是一周的哪一天，并转化为对应的数字，如周一为1，周二为2。用较大数减去较小数。评价方法如表1所示。

表1 每周共有2课次的科目的评价方法

③科目j每周共有3课次。分别计算出3个课次对应的是一周的哪一天，转化为对应的数字并从小到大排列。对相邻的两个数，用较大数减去较小数，得到两个差值。评价方法如表2所示。

表2 每周共有3课次的科目的评价方法

（3）同一小班的课程应尽量均匀安排在每一天

对于小班i，统计该班一周内每天的课次数，计算出标准差，标准差的值越小，安排的效果越好。评价函数如下：

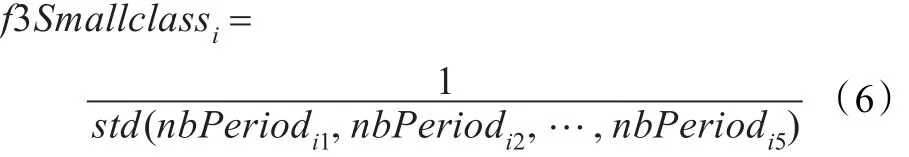
若标准差为0，则将f3Smallclassi赋值为3。

（4）教室的利用率

计算所有已有安排的教室的平均利用率。评价函数如下：

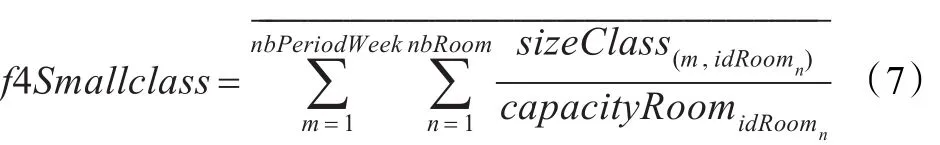
则总的评价函数为：

这种评价方式可以进一步扩大科目数量更多、科目重要程度更高、每周总课次更多的小班在目标函数中所占的比重，使这些小班在排课过程中具有更高的优先级。以该函数作为本文混合遗传算法的适应度函数，函数值越大，解就越优。

3 高校排课问题的混合遗传算法设计

3.1 编码方法

排课问题是要把各个班级、科目和教师安排在合理的时间和地点，即时间段和教室。建立以每周总时间段数nbPeriodWeek为行数，以教室总数nbRoom为列数的二维矩阵，矩阵中的每一个非空位置的元素都包含了三个变量：班级编号，科目编号和教师编号。没有元素的位置则表示该时间段的该教室没有安排。采用这种编码方式可以直接满足第三个硬约束条件）。编码方法如图1所示。

3.2 初始种群的产生

每一个初始可行解即为初始种群中的一个个体。每一个可行解的产生过程如图2所示。

图1 编码方法

图2 可行解的产生过程

按照本文产生可行解的方法，若先安排每周课次较多的班级，由于解空间被过早压缩，容易导致后面的班级无法被安排，即无法产生可行解。因此在进行排课之前，先把各个班级按照每周课次从小到大的顺序进行排序，这样就避免了解空间的过早压缩，能够很快地产生可行解。

如果在每次产生可行解的过程中班级的顺序都固定不变，那么不同的可行解之间难免会具有一定的相似性，这样就使得遗传算法容易陷入局部最优解，不利于全局的搜索。因此，有必要进行一定的乱序处理，使不同的个体之间具有比较大的差异，这样才能使遗传算法能够在范围更大的解空间内进行搜索，以找到全局最优解。

本文采取的乱序处理有两个步骤。首先，在各个班级按照每周课次从小到大的顺序进行排序后，把每周课次相同的班级分为一组，在组内进行随机的重新排序。如图3和图4所示。

图3 乱序处理前的班级编号

图4 乱序处理后的班级编号

然后，对于每个班级的所有科目，在排课过程中也进行随机的重新排序，如图5所示。

图5 科目的乱序处理

3.3 选择算子

本文的选择算子引入了保留最优个体策略，即适应度最高的个体直接进入下一代，其余进入下一代的个体通过赌轮盘法选出。对种群中的每个个体进行评价，适应度越高的个体越有可能进入下一代种群。把个体i的适应度记为fi，则该个体进入下一代种群的概率为：

其中nbIndividual为一代种群中个体的数量。

3.4 交叉算子

每个可行解都是在满足了许多约束条件的情况下产生的，若交叉操作的规模较大，则产生的子代很容易是一个非可行解，因此本文采用了两点交叉操作。此外，为了保证交叉操作对解的改进作用，本文还引入了竞争机制。具体操作过程如下。

（1）对于两个将要进行交叉操作的个体父代1（个体i）和父代2，找出它们对应的矩阵中都有安排、且坐标相同、且对应的科目编号不同的位置，把这些位置作为交叉操作的候选位置。

（2）从候选位置中随机选出一个位置，记父代1和父代2在该位置对应的元素分别为元素1和元素2，交换该位置的元素1和元素2。则父代1中了多了一个元素2，少了一个元素1；父代2中多了一个元素1，少了一个元素2。从父代1中找出其他位置的元素2，放入集合1；从父代2中找出其他位置的元素1，放入集合2。从集合1中任选一个元素2，从集合2中任选一个元素1，将它们在两个子代个体中的位置进行交换。交叉和修正的过程如图6所示。

图6 交叉操作过程

由于集合1和集合2的规模都很小，为了保证交叉操作的质量，这里采用局部遍历的方式将集合1中的元素2和集合2中的元素1按照它们在各自集合中的次序逐个进行交换，直到某一次交叉操作产生的两个子代个体都是可行解，则把它们与两个父代个体都存放在集合GenerationTemp中，停止遍历，交叉过程结束。

（3）引入竞争机制，对集合GenerationTemp中的2个父代个体和2个子代个体逐一进行评价，从中挑选出表现最好的一个，作为本次交叉操作最终得到的最优个体，进入下一代种群。

此外，为了控制运算的时间，设置了进行交叉操作的尝试次数限制。交叉操作的流程如图7所示。

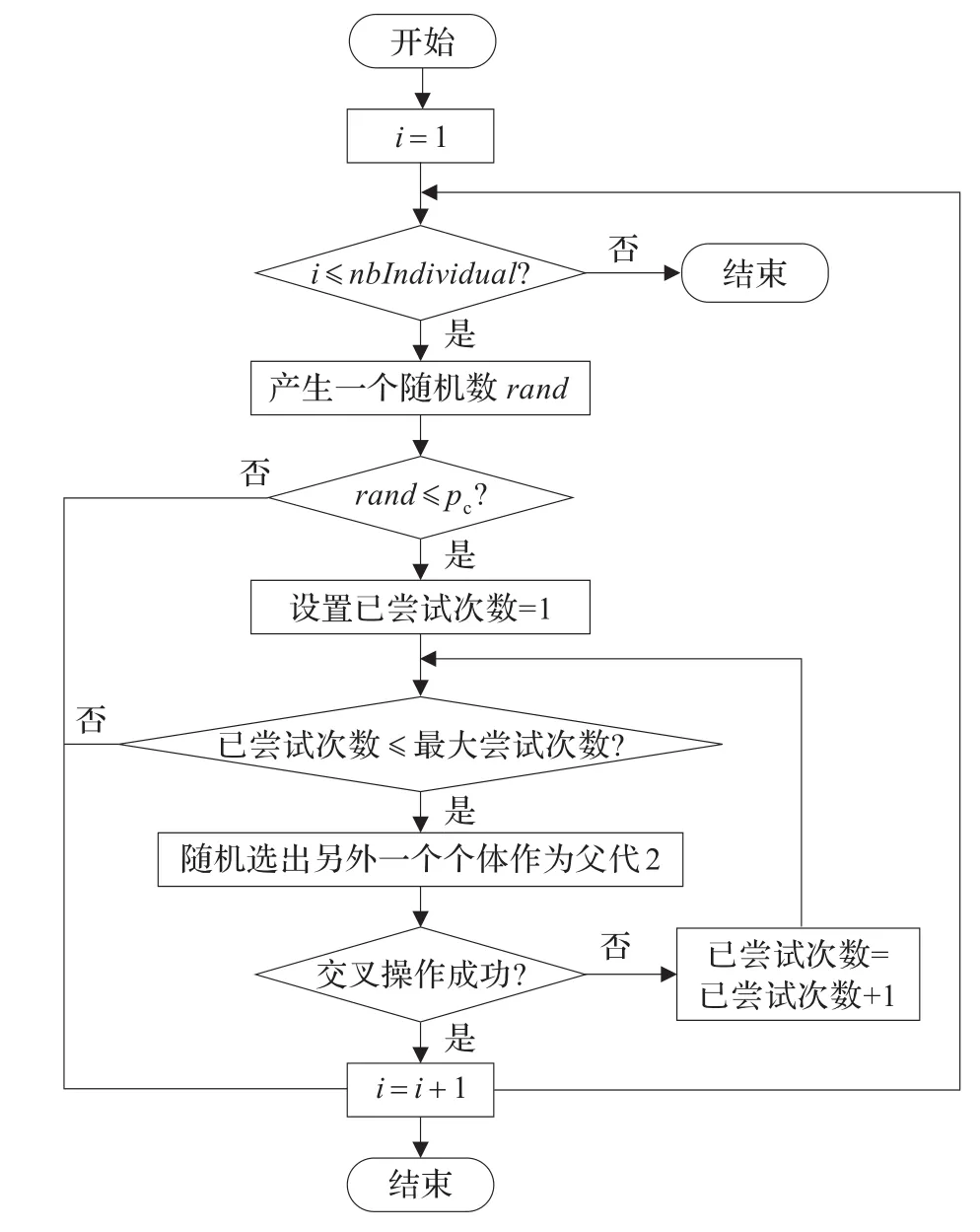
图7 交叉操作流程图

3.5 变异算子

对于要进行变异的父代个体，在其矩阵中随机选出两行，交换这两行的元素，产生一个新的个体。由本文的编码方式可知，经过这种变异操作所产生的子代也是可行解。变异的过程如图8所示。

图8 变异操作过程

图9 模拟退火过程

3.6 种群的进化

种群进化的流程如图10所示。

3.7 检查机制

为了验证算法的可行性，本文引入了4个检查机制：

（1）每个时间段是否有同一个班级出现在不同的教室。

（2）每个时间段是否有同一名教师出现在不同的教室。

图10 种群进化的流程图

（3）每个教室的容量是否不小于在此上课的班级的总人数。

（4）一个解中所有元素的个数是否等于所有班级的总课次数。

检查结果显示，种群中的每一个个体都满足了所有的硬约束条件，并且没有任何班级、教师或科目存在安排遗漏的情况。

4 实验例证

4.1 实例数据

本文的实验数据来自于XX大学XX学院2013—2014学年秋季课程安排，共包括79个班级（其中包括93个不同的小班），145门科目，85名教师，18间教室。

4.2 参数设置

初始种群规模nbIndividual=100，迭代次数nbIteration=180，交叉概率pc和变异概率pm采用了自适应参数设置。

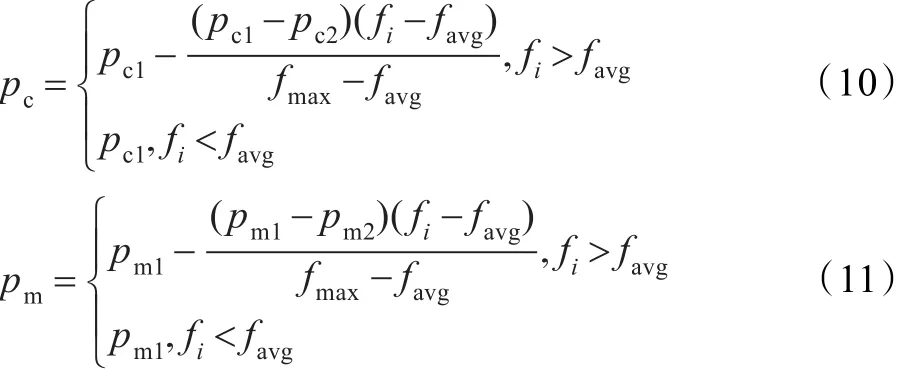
其中pc1=0.9，pc2=0.6，pm1=0.2，pm2=0.02，fi为要进行交叉或变异操作个体的评价值，favg为当前种群的平均评价值，fmax为当前种群的最大评价值。

由于标准模拟退火算法需要消耗很长的时间，而本文主要是借鉴模拟退火算法的思想，因此和模拟退火算法有关的参数设置较小。初始温度t0=100，最低温度tmin=0.1，退火系数a=0.9，温度下降方式为t=t×a，每个温度下对邻域解的搜索次数为1。

4.3 实验结果

对于同一初始种群，分别用4种方法对其进行优化：（1）文献[23]的改进遗传算法，记为GA1；（2）本文所设计的遗传算法，记为GA2；（3）全局引入模拟退火算法的遗传算法；（4）局部（前50次迭代）引入模拟退火算法的遗传算法。进化情况如图11所示。

图11 同一初始种群在不同算法下的优化效果

从图11中可以看出，本文所设计的遗传算法有效地避免了种群的退化，并且跳出了局部最优解，在更大的解空间内搜索到了更好的解。在引入具有跳变能力的模拟退火算法之后，搜索的效率得到了进一步的提高。由于在算法的前期应当尽量扩大搜索范围以提高找到更优解的概率，而在中后期则应集中对局部解空间的搜索，因此本文又尝试仅在进化前期引入模拟退火算法以增大搜索范围，而在中后期只使用遗传算法以加强局部搜索，进一步提高了解的质量。分别把方法（1）和（4）得到的各项评价指标进行对比，如表3所示。

表3 评价指标比较

表3中各评价项目的计算方法如下。“教学时间段的安排效果（每天第1、3和5个教学时间段）”的计算方法是：对于一周内每天的第1、3和5个教学时间段，找出在这些时间段有教学安排的所有教室，用在该教学时间段和该教室上课的班级的小班数目乘以所学习科目的学分，作为相应的科目安排效果的评价值，最后将所有教学时间段的所有教室的科目安排效果评价值相加。“科目的安排效果”的计算方法是：分别计算出每个小班的科目的安排效果，然后再取平均值。“总课次的均匀程度”的计算方法是：分别计算出每个小班在一周内每天总课次的标准差，然后再取平均值。

从表3中可以看出，每天教学效果最好的时间段，即第1，3和5个教学时间段，得到的评价值要明显高于第2和4个教学时间段，达到了重要程度更高的科目被安排在教学效果更好的教学时间段的目的。科目的安排效果和教室利用率都得到了改进，课次的分布也更为均匀。这里的教室利用率是一个接近50%的数值，说明学生在上课时能够基本以间隔一个位置的方式就坐，这样学生上课的舒适度会更高。

5 结束语

对于高校排课问题，合班教学是一个广泛存在的现象，本文针对这个特点对问题进行了数学建模，并设计了引入模拟退火算法的混合遗传算法进行求解，使两种算法能够互相弥补。实验结果表明，与一般的遗传算法相比，本文提出的混合遗传算法具有更高的搜索效率。

遗传算子的方法设计并不只有一种，遗传算法与其他智能算法的结合也有多种选择，如何设计出合适的算子以及与更多智能算法相结合，是下一步将要研究的重点。

[1]Even S，Itai A，Shamir A.On the complexity of time table and multi-commodity flow problems[J].SIAM Journal of Computation，1976，5（4）：691-703.

[2]Carter W M，Tovey C.When is the classroom assignment problem hard?[J].Operations Research，1989，40（S1）：28-39.

[3]Junginger W.Timetabling in Germany-asurvey[J].Interface，1986，16（4）：66-74.

[4]Neufeld G A，Tartar J.Graph coloring conditions for the existence of solutions to the timetable problem[J].Communications of the ACM，1974，17（8）：450-453.

[5]de Werra D.An introduction to timetabling[J].European Journal of Operational，1985，19（2）：151-162.

[6]Shih W，Sullivan J A.Dynamic course scheduling for college faculty via zero-one programming[J].Decision Sciences，1977，8（4）：711-721.

[7]McClure R H，Wells C E.A mathematical programming model for faculty course assignments[J].Decision Sciences，1984，15（3）：409-420.

[8]Tripathy A.School timetabling-a case in large binary integer linear programming[J].Management Science，1984，30（12）：1473-1489.

[9]Ostermann R，de Werra D.Some experiments with a timetabling system[J].OR Spectrum，1982，3（4）：199-204.

[10]Mulvey J M.A classroom/time assignment model[J].European Journal of Operational Research，1982，9（1）：64-70.

[11]Yu E，Sung K S.A genetic algorithm for a university weekly courses timetabling problem[J].International Transactions in Operational Research，2002，9（6）：703-717.

[12]Ueda H，Ouchi D，Takahashi K，et al.Comparisons of genetic algorithms for timetabling problems[J].Systems and Computers in Japan，2004，35（7）：1-12.

[13]Kohshori M S，Liri M S.Multi population hybrid genetic algorithms for university course timetabling[J].International Journal for Advances in Computer Science，2012，3（1）：12-22.

[14]Liu Y，Zhang D，Leung S C H.A simulated annealing algorithm with a new neighborhood structure for the timetabling problem[C]//Proceedings of the 1st ACM/SIGEVO Summit on Genetic and Evolutionary Computation，2009.

[15]Minh K N T T，Thanh N D T，Trang K T，et al.Using tabu search for solving a high school timetabling problem[M]//Studiesin computationalintelligence，2010：305-313.

[16]Jat S N，Yang S.A hybrid genetic algorithm and tabu search approach for post enrolment course timetabling[J].Journal of Scheduling，2011，14（6）：617-637.

[17]Chiarandini M，Birattari M，Socha K，et al.An effective hybrid algorithm foruniversity course timetabling[J].Journal of Scheduling，2006，9（5）：403-432.

[18]汪晓飞，李晓宁.GA编码方案在高校排课系统中的应用[J].计算机工程与设计，2008，29（17）：4565-4567.

[19]李红蝉，朱颢东.采用十进制免疫遗传算法求解高校排课问题[J].系统工程理论与实践，2012，32（9）：2031-2036.

[20]王小平，曹立明.遗传算法——理论、应用与软件实现[M].西安：西安交通大学出版社，2002.

[21]王凌.智能优化算法及其应用[M].北京：清华大学出版社，2004.

[22]LewisR.A survey ofmetaheuristic-based techniques foruniversity timetabling problems[J].OR Spectrum，2008，30（1）：167-190.

[23]李红蝉，朱颢东.基于最佳个体置换策略的高校排课问题求解[J].计算机工程，2011，37（19）：186-188.