二维翻转结构9/7离散小波逆变换研究与VLSI实现

宋有才 ，谭拂晓 ，王诗兵 ，韩 波 ，2，赵正平

1.阜阳师范学院 计算机与信息学院，安徽 阜阳 236037

2.东南大学 毫米波国家重点实验室，南京 210096

1 引言

二维9/7离散小波变换（Discrete Wavelet Transform，DWT）与逆变换（Inverse Discrete Wavelet Transform，IDWT）以优越的显示效果、良好的压缩比、多分辨率等特性而广泛应用于各类图像处理中。传统上，离散小波变换通过卷积实现，Daubechies和Sweldens提出了离散小波变换的提升结构[1-2]，极大地降低了计算量与复杂度。以9/7离散小波逆变换为例，其实现步骤如下：

（1）系数伸缩：

（2）一级提升：

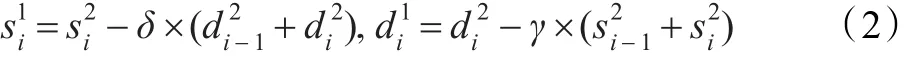
（3）二级提升：

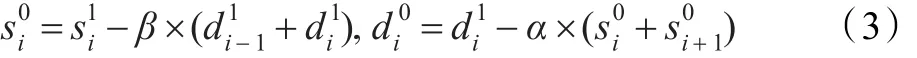
（4）数据输出：

式中，α=-1.586 1，β=-0.052 98，γ=0.882 9，δ=0.443 5，K=1.149 6。与分别为偶数行与奇数行小波系数。与分别为逆变换后的偶数行与奇数行原始信号。所谓的二维IDWT，即是基于公式（1）到（4）先沿着行方向进行一维IDWT，再沿着列方向完成二维IDWT。尽管提升结构9/7离散小波逆变换通过一组加法与乘法实现，极大地降低了算法复杂度，但随着高清图像实时处理、编解码的广泛应用，对计算过程中的内存消耗、计算速率提出了更高要求。国外文献[3-6]也是以此研究方向，先后从算法优化、电路结构等方面展开了优化，但效果有限，没有实现性能的综合提升。国内的众多研究结构也就该领域展开了一系列的研究[7-16]。

本文的创新点在于：通过研究算法结构与分析数据输入输出格式，提出了一种适合电路建模的翻转结构。在此基础上，采用流水线技术，将关键路径降为1级乘法器延时；设计了多核结构，并行地完成行列方向逆变换，在提高处理速率的同时，处理N×N图像仅需4N的内存消耗。

2 翻转结构IDWT

电路实现过程中，如何将IDWT的计算过程分解融入到各级流水线中，直接影响了电路的关键路径延迟，从而决定了电路的运行时钟。IDWT运算类型虽仅有乘法和加法，但一般情况下，乘法运算通过专用乘法器实现，比起电路模型中的其他基本逻辑运算，最影响关键路径延迟。因此，计算过程的优化思路就进一步集中在如何分割乘法运算到各级流水线实现。

分析公式（2）与（3），在进行乘法运算前，首先需要进行一次加法运算。尽管可以通过流水线来优化，但是数据须先后流经乘法计算路径与加法计算路径，增加电路设计时的复杂度。为此，本文提出下式所示的计算过程：

（1）系数伸缩：

（2）一级翻转

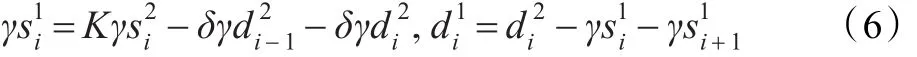
（3）二级翻转：

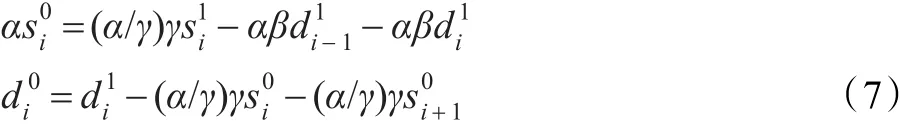
（4）数据输出：

式中各参数定义和取值与基本提升结构相同。Kγ、α-1、K-1、δγ、α/γ与αβ六个乘法系数可以提前计算得到。所谓的翻转结构就是将公式（2）与（3）中第二个算式的提升系数翻转，从而将计算路径分割为乘法路径和加法路径两个部分，流水线设计时可在第一个周期完成乘法，之后只需进行几次加法即可，便于电路实现。同时，上述翻转结构按正常顺序读入和输出数据，两级翻转仅翻转系数不同，便于电路结构的复用。

3 VLSI设计

3.1 系统架构

基于本文提出的翻转结构IDWT，设计电路系统架构如图1所示。包括行方向一维逆变换核、数据流组织模块、列方向一维逆变换核三部分。处理时，小波子带系数按行方向顺序输入，进行一维行方向逆变换。数据缓存模块仅需缓存2N的中间数据，即可流水线地进行一维列方向逆变换。每级小波逆变换结束后，输出的LL子带系数可返回至输入内存，用于上一级小波逆变换。如此反复，直到获取原始图像。下面将详细介绍各模块的电路实现。

3.2 行方向逆变换核

一级翻转结构行方向逆变换的电路原理如图2所示。图中，⊕表示加法器，⊗表示乘法器，□表示寄存器。假设伸缩变换后的与已经读入，则在第t个周期内与δγ完成乘法进入d2，则缓存在reg中；第t+1周期，完成与的减法存入s_temp，同时读入并完成与δγ的乘法存入d2中；第t+2个周期，s_temp缓存数据与d2缓存数据相减，获得。为了对齐时钟，在输出前加了一级寄存器，即在t+4个周期同时输出与。参考公式（6）与图2同样可知的计算过程。显然，由于流水线技术的使用，在每个时钟周期内仅需完成一个计算步骤，关键路径为一级乘法器延迟。通过以上分析，该电路单元共采用了4级流水线，共需1个乘法器、4个加法器和9个寄存器。

图1 整体处理架构

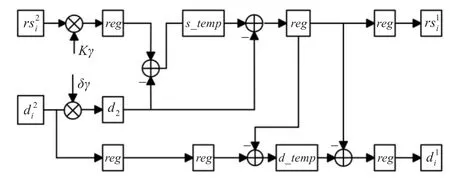
图2 一级翻转结电路原理

比较公式（6）与公式（7），两者计算过程相近，仅仅是乘法系数不同。因此，可通过选择器选择乘法系数，从而复用一级翻转结构的电路实现。完整的两级翻转结构逆变换过程如图3所示。

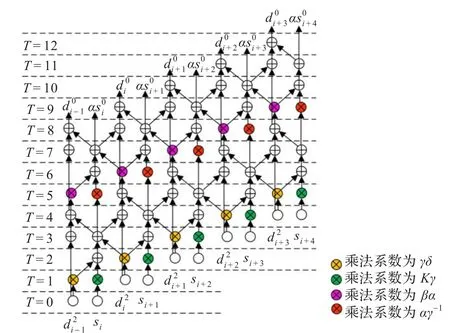
图3 完整的两级翻转结构变换过程

3.3 列方向逆变换核

不失一般性的，以6×6图像处理过程为例说明变换列方向逆变换核的电路结构。理论上，一维列方向逆变换电路结构与一维行方向逆变换电路结构基本相同。但一维列方向小波逆变换是逐列进行，而一维行方向小波逆变换是逐行输出，如图4（a）所示。为了在有效提高电路并行度的同时有效降低数据缓存模块大小，在缓存相邻两行共2N的一维列方向小波逆变换结果后，立即如图4（b）所示按列两两读入进行一维列方向小波逆变换，其中，黑框部分是采用周期对称延拓的边界数据。根据上一节分析，s_temp和d_temp分别需要缓存N/2数据。但在此之后，每输入2个一维行方向逆变换的结果，便可继续流水线的完成操作。其关键路径仍为1个乘法器延时，流水线仍为4级，数据缓存模块共消耗2N的转换内存。

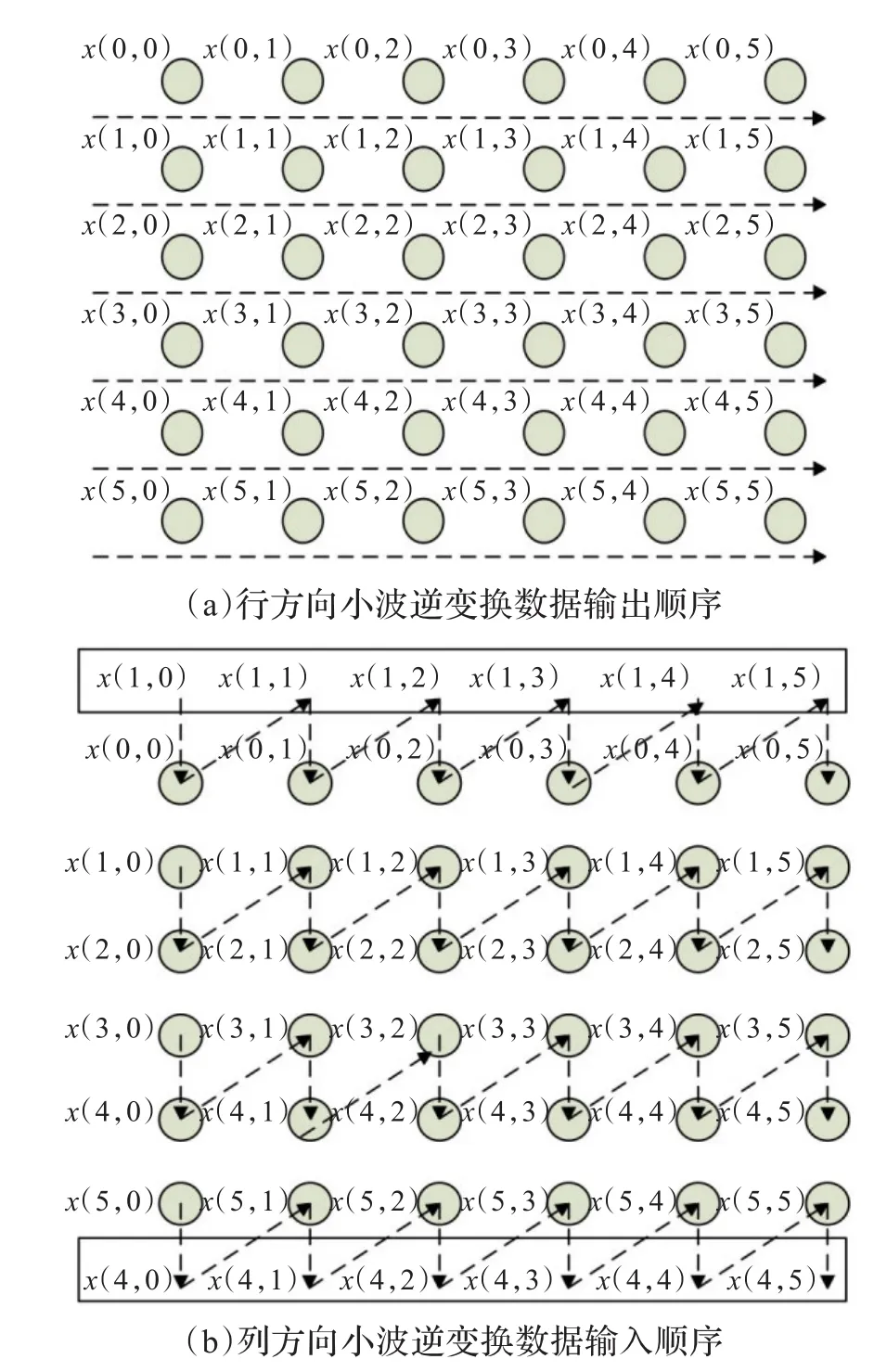
图4 数据缓存模块处理流程

4 实验分析

采用Verilog语言实现本文描述电路，基于Sparten6-xc6slx150t FPGA平台，在Xilinx ISE下仿真验证，模块运行时钟达166.34 MHz。选取相关文献中列出的研究成果进行比较，如表1所示。其中，Tm是指乘法器延时，Ta是指加法器延时。本文所提出的翻转结构9/7离散小波逆变换及其实现电路在得到最小内存消耗的同时具有最小的关键路径，综合性能最佳。

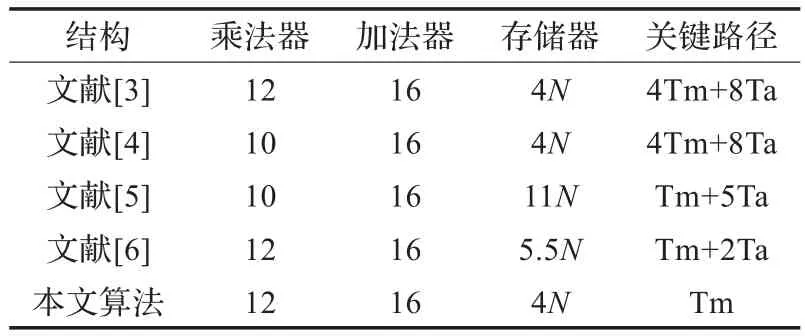
表1 性能分析

5 总结

本文研究了一种新的翻转结构二维9/7离散小波逆变换，并综合了流水线技术与并行技术，设计了一种高性能的VLSI结构，以满足高清实时图像处理的需要。

[1]Daubechies I，Sweldens W.Factoring wavelet transform into lifting steps[J].J Fourier Anal Appl，1998，4（3）：247-269.

[2]Sweldens W.The lifting scheme：a custom-design construction of biorthogonal wavelets[J].Applied and Computation Harmonic Analysis，1997，15（3）：186-200.

[3]Liao H，Mandal M K，Cockburn B F.Efficient architectures for 1-D and 2-D lifting-based wavelet transforms[J].IEEE Transactions on Signal Processing，2004，52（5）：1315-1326.

[4]Tseng P C，Huang C T，Chen L G.Generic RAM-based architectures for two-dimensional discrete wavelet transform with line-based method[J].IEEE Transactionson Circuits and Systems for Video Technology，2005，15（7）：910-920.

[5]Huang C T，Tseng P C，Chen L G.Flipping structure：an efficient VLSI architecture for lifting-based discrete wavelet transform[J].IEEE Transactionson Signal Processing，2004，52（4）：1080-1089.

[6]Li W M，Hsia C H，Chiang J S.Memory-efficient architecture of 2-D dual-mode discrete wavelet transform using lifting scheme for motion-JPEG2000[C]//ISCAS 2009.Taipei，China：IEEE，2009：750-753.

[7]陈旭昀，周汀，闵昊.二维DWT/IDWT处理器的VLSI设计[J].电子学报，1997，25（2）：29-32.

[8]孟军，魏同立，吴金，等.数字图像离散小波变换的原理与硬件实现分析[J].东南大学学报：自然科学版，2002，32（6）：842-847.

[9]熊承义，田金文，柳健.一种基于提升算法的小波滤波器硬件结构设计[J].华中科技大学学报：自然科学版，2003，31（9）：82-83.

[10]陈大科，韩九强.5/3提升小波变换及逆变换的FPGA设计方法[J].东南大学学报：自然科学版，2005，35（SupII）：211-214.

[11]赵楠楠，孙红星，徐心和.改进的基于提升格式的DWT硬件实施方案[J].东北大学学报：自然科学版，2006，27（6）：606-609.

[12]曹鹏，王超，李杰.一种高效的多级递归提升离散小波变换VLSI架构[J].应用科学学报，2007，25（5）：475-480.

[13]郝燕玲，刘营.改进的离散小波变换流水线VLSI结构[J].华中科技大学学报：自然科学版，2008，36（12）：8-11.

[14]王巍，杜治芸，曾勇.9/7提升小波变换图像处理算法的高速FPGA实现[J].微电子学，2009，39（6）：852-856.

[15]曹鹏，王超.高性能低存储的2维离散小波变换架构[J].中国图象图形学报，2009，14（11）：2198-2204.

[16]高志荣，熊承义.提升小波变换的并行处理与高速实现[J].光电工程，2009，36（8）：112-122.