基于三角网格模型的复杂曲面测点规划
陈岳坪,靳龙,卢海燕,陈艺
(1.广西科技大学机械工程学院,广西柳州545006;2.柳州市产品质量监督检验所,广西柳州 545001)
0 前言
随着航空、航天、汽车、模具等现代工业的飞速发展,越来越多的零件采用复杂曲面的形式[1]。对复杂曲面零件的检测是实现复杂曲面零件设计制造与形状检测的关键步骤之一。评价一种曲面测量方法优劣的标准,主要看该方法能否适应曲面特征而进行高效高精度的测量[2]。检测系统中测点的数目和布局是否合理,将直接影响系统的测量精度和测量效率。
三角网格模型是由三角面片组成的分片线性曲面模型,通常用STL(Stereo Lithographic)文件格式进行实体表面数据的描述,己成为CAD/CAM系统的一类标准接口文件格式,大多数商用CAD/CAM系统都具备其几何模型的STL文件输出。本文作者将基于曲面零件的三角网格模型 (STL文件格式)研究检测过程中的测点规划方法。
1 曲面测量的截面线生成
1.1 基于截面线法的测量原理
曲面测量实现的要求是可行、安全、高效,同时也要尽量使测点分布的疏密与曲面的曲率变化相适应,并使测量结果便于后续的曲面加工精度评价。曲面测量方法可以采用基于“曲面-曲线-点集-测量点集”的递归分解策略一行一行地测量,即截面线法。截面线法[3]是指用一组平行平面与被测曲面相交,沿截交线对曲面进行测量。测量原理如图1所示。这些平行平面 (截面)与CAD模型相交,可以得到一系列的交线;然后在这些交线上按照一定的规则取点即可以作为测点,如图2所示。

图1 截面线法测量原理

图2 在截面线上取点
1.2 网格模型的截面线生成
基于STL三角网格模型的截面线法实现过程是,首先给定平行截面族的空间方位,确定与目标平面相交的一个初始三角网格,并利用三角形面片的拓扑关系,快速找出与其相交的所有网格的集合;然后通过线面截交计算得到触测点。最后,通过曲线反求方法得到插值曲线,最终计算出全部触测点的坐标。
文中提出截面线法的具体实现方法是中点偏移抛物线法。中点偏移抛物线法是根据网格顶点的插值边界曲线与检测截面的交点计算精确的触测点。
2 基于中点偏移抛物线法的触测点生成
三角网格曲面是对原始模型的线性逼近,三角网格的边线也只是逼近原始CAD模型,文中提出的中点偏移抛物线法原理如图3所示。截平面M与三角网格模型相交,截平面不是采用与三角网格模型的边线相交,而是在边线的两个端点间构造一段抛物线(二次贝塞尔曲线),该抛物线可进一步逼近原始CAD模型,交点由抛物线与截平面相交产生。如图3所示,采用截平面与抛物线线相交,分别得到3个交点P0、P1和P2。这3个交点可以近似认为就是理想CAD模型上的点。然后对这些交点按照一定的顺序(如按y坐标)进行排序,可得到一系列的坐标点,后续把这些坐标点作为型值点,采用曲线反求方法得到插值曲线,从而最终计算出全部触测点。

图3 中点偏移抛物线法原理
(1)构造抛物线。中点偏移抛物线法的关键是构造若干段抛物线逼近原始CAD曲面模型。如图4所示,设V0V1为与检测截面相交的网格边,求出V0V1的中点Vm的偏移点V,以V0、V1和V为控制点,采用下式所表示的抛物线方程逼近网格边V0V1。通过迭代计算网格边界曲线与检测截面的交点获取检测接触点。

图4 抛物线的构造

V点的确定方法说明如下:设顶点法矢n0和n1与向量V0V1的方向夹角分别为θ0和θ1。如图5所示,当θ0=θ1时,可以认为V就在V0V1连线的中点Vm上。如图6所示,当θ0>θ1时,可以认为连接V0V1的这段曲线是外凸的,V是以V0V1连线的中点Vm为基础,偏移了一个距离,其大小为:

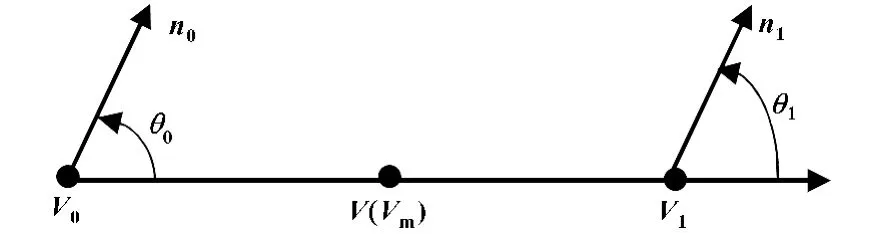
图5 中点偏置方法 (当θ0=θ1时)

图6 中点偏置方法 (当θ0>θ1时)
偏移的方向矢量为:

偏移的单位方向矢量为:

故V点的坐标为

其中

当θ0<θ1时,可以认为连接V0V1的这段曲线是内凸的,上面的V点计算公式仍然适用。
(2)求截平面与抛物线的交点。如图3所示,实际的触测点不是目标平面与网格边界的交点,而是与网格边界插值曲线 (抛物线)的交点。这些边界曲线采用中点偏移抛物线方式给出。然后采用数值分析中的二分法,根据边界曲线和截平面方程求出曲线与平面间的交点,这样就得到了精确的触测点坐标,计算交点的过程说明如下。
设截平面方程为:cx+λy+qz+g=0,同时定义符号函数为:

其中:c,λ,q,g为平面方程系数。
二分法的基本思想是,将与截平面相交的网格边界的两端点作为含有交点的区间,将此区间二分,通过判断符号函数的正负,进一步探索有根区间,将有根区间缩小到充分小,当该区间达到规定长度时,求得交点的参数值tc,便得到了交点即实际触测点Pc的坐标

为了验证上述中点偏移抛物线法的有效性,图7给出了某三角网格曲面的触测点生成效果。用某一截面与该三角网格相交,在曲面上共生成了70个触测点。
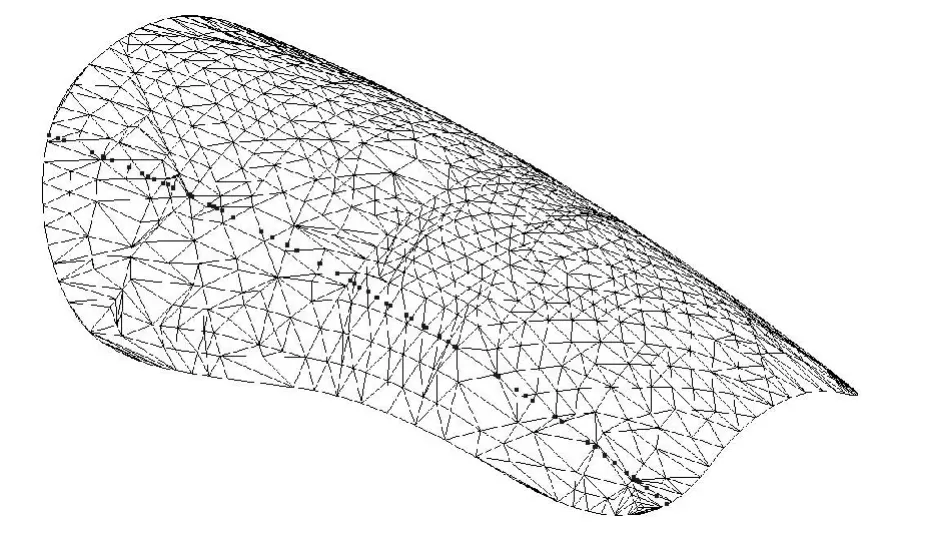
图7 基于三角网格的触测点生成实例
3 基于触测点反求插值法的截面线生成
通过线面求交求出一系列的触测点之后,还要对这些触测点按照一定的顺序进行排序。为了进行后续测点的自适应规划,还要对这些排序后的触测点进行反求插值,目的是得到通过这些测点的截面线的参数表达式。文中采用曲线拟合法中的B样条曲线来拟合这些离散测点数据,这种曲线有很多优点,如[4]:局部支撑性、凸组合性质、拟合曲线的线性变换条件下的几何不变性、节点处良好的连续性等。
B样条曲线反求可以采用两种方法[5-6]:均匀B样条曲线和非均匀B样条曲线。均匀B样条曲线的节点矢量中节点为沿参数轴均匀分布或等距分布;而非均匀B样条曲线的节点矢量中节点沿参数轴一般不是均匀分布或等距分布。
由于用平行截面对三角网格模型进行线面截交得到的数据点,往往分布不均匀,如果用均匀B样条控制点反求方法反求控制点,将无法得到理想的结果,所以针对非均匀数据点,采用累加弦长参数化法来构造非均匀节点矢量。这种参数化方法如实反应了数据点按弦长分布的情况,克服了数据点在分布不均匀的情况下,采用均匀参数化所出现的问题。
4 基于截面线曲率变化的测点自适应规划
检测点数量和分布的确定是紧密联系在一起的,复杂曲面的测点数可以通过经验来确定。为了方便测量,更好的完成测点数的确定过程,可以通过输入法确定测量点数,该输入值作为测点自适应分布的保留点数。对于已知解析式的曲线、曲面,采用弦高法来实现测点自适应分布。
如图8所示,曲面上有两点A、B,若这两点的曲率大,则两点之间的弦高数值也大;若这两点的曲率小,则两点之间的弦高数值也小。因此可以用弦高来度量两点之间的曲率,实现测点的自适应分布。方法如下:给定点A(u,v),B(u+Δu,v),求弧长与弦AB的最大距离 (弦高)d。
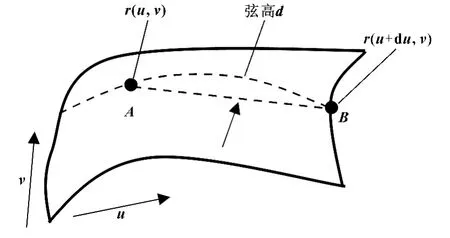
图8 弦高法
(1)若d>ε,则缩小A、B之间的距离,取ub=ub-δ,又重新计算d。其中ε为允许的弦高,δ为预先指定的任意小量。不断进行上述计算,直到d<ε的条件满足,则可把B点计入测点集并将其作为当前点,在整条曲线上重复上述过程,这样就可以实现当前曲线的测点自适应分布。
(2)用上述类似的方法求出测点沿v向的最小进给步长,以此确定下一曲线的位置,然后按照上述的方法进行该曲线的测点自适应规划;在整个曲面上重复上述过程,这样就可以实现整个曲面上的测点自适应分布。
5 测点规划的实现步骤与实例验证
图9给出了复杂曲面测点规划布局的详细步骤。为了验证所提出的测点规划方法,以Visual C++6.0为开发工具,采用典型解析曲面的离散网格进行了测点生成的仿真实验。为了便于比较,对同一个复杂曲面 (形状如图10所示),分别在UG软件中生成3种不同精度的STL网格模型,这3种精度分别为0.08、0.04和0.02 mm。
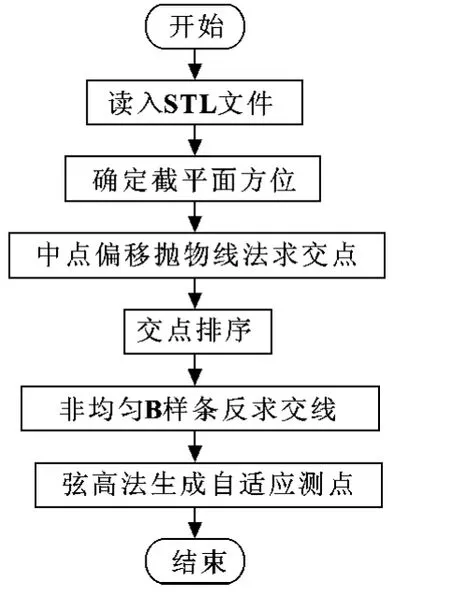
图9 测点规划流程图

图10 原始CAD模型曲面
用若干个等间距的平行截面截交三角网格模型,即可得到一系列的线面相交的测点坐标,图11给出了对网格精度为0.08 mm三角网格曲面,采用20个平行截面截交该模型得到的测点情况。对这些测点采用非均匀B样条曲线进行反求,得到一系列的反求插值曲线,如图12所示为网格精度为0.08 mm的反求插值曲线。

图11 线面相交后的测点

图12 对交点进行曲线反求后的插值曲线
接着,按照弦高法进行测点规划,结果如图13所示。从图13可以看出,曲率变化大的位置测点分布比较密集,曲率变化小的位置测点分布比较稀疏。同时也可以看出,测点的分布密度与网格的分布密度是相关的,即曲率变化大的位置网格分布比较密集,曲率变化小的位置网格分布比较稀疏,实际上这是符合三角网格的生成原则的。因而,弦高法可以实现针对三角网格模型曲面的截面曲线上测点的自适应分布。

图13 网格精度0.08 mm的测点规划
生成自适应分布的测点后,须对曲面的测点坐标做误差分析。测点坐标误差用所求测点到理论曲面的距离来表示。经计算后,精度分别为0.08、0.04和0.02 mm的网格模型,测点的坐标误差如表1所示。
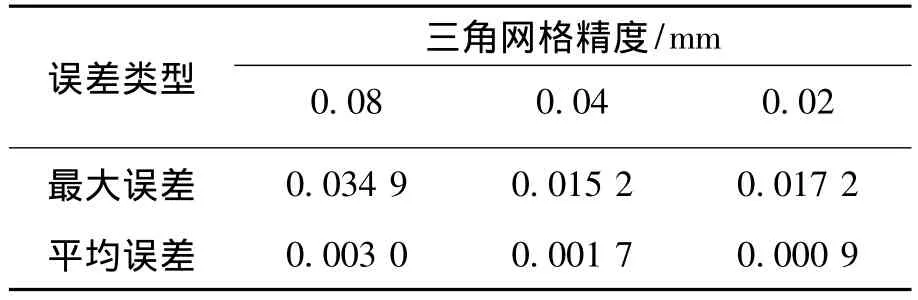
表1 生成测点的坐标误差
从表1可以看出:当三角网格精度为分别为0.08、0.04和0.02 mm时,则相应的测点坐标误差的平均值分别为0.003 0、0.001 7和0.000 9 mm。本文提出的中点偏移抛物线法,能有效计算测点的坐标;并且测点的坐标计算精度与三角网格本身的精度密切相关,三角网格本身的精度越高,则测点的计算精度越高,因此尽可能采用精度高的三角网格模型,但这将使计算效率降低。
6 结论
基于三角网格文件格式的曲面零件模型,探讨了测量点分布与测量效率的关系;根据零件三角网格模型的几何特性,对基于截面线法的测点生成技术,提出采用中点偏移抛物线法的具体实现方法,逼近原始CAD曲面;在对测点规划方法进行分析的基础上,提出基于截面线弦高法的按曲率分布测点算法,可有效实现检测系统测量点的合理分布。
[1]郑惠江,何改云,丁伯慧.离散数据环境下复杂曲面检测点布局策略研究[J].机械工程学报,2011,47(24):8-14.
[2]丁汉,朱利民,熊振华.复杂曲面快速测量、建模及基于测量点云的RP和NC加工[J].机械工程学报,2003,39(11):28-37.
[3]鞠华,王文,谢金.逆向工程中自由曲面的自适应数字化算法研究[J].计量学报,2003,24(2):99-102.
[4]王先培,张爱菊,李少雄.基于非均匀B样条曲线的红外数据的精确拟合及校正[J].光谱学与光谱分析,2006,26(10):1850-1853.
[5]张红.三次B-spline曲线反求的实现[J].广东石油化工专科学校学报,1995(1):27-31.
[6]慈瑞梅.基于CMM测量数据的曲面重构关键技术研究与实现[D].南京:南京理工大学,2005.

