基于NC代码的数控渐进成形有限元分析轨迹点提取研究
李佳良,朱虎,李华溢
(沈阳航空航天大学机电工程学院,辽宁沈阳 110136)
0 前言
金属板材数控渐进成形是根据分层制造原理,使挤压工具沿着预先编制好的轨迹,逐层逐点挤压板材使其发生局部塑性变形,进而渐进地完成板材件成形的一种无模成形技术[1-2]。有限元分析方法是数控渐进成形过程数字模拟、成形性能分析、成形参数优化和成形结果预测及缺陷诊断的有力工具[3-8],其关键是正确地描述挤压工具的运动[9]。然而,由于数控渐进成形的挤压工具运动非常复杂,现有的有限元分析软件无法直接对其进行准确描述,也不能直接利用NC代码进行有限元分析,因而很难进行复杂板材件的数控渐进成形有限元分析。李磊等人[10]利用Mat-Lab获取圆锥形模型数控渐进成形过程有限元分析所需轨迹点,然而这种方法仅适用于形状结构比较简单的板材模型。李珑杲等[9]采用“虚拟靠模导向法”生成了有限元分析中所需的挤压工具运动路径。史晓帆等[11]利用商业CAD/CAM软件后处理中的线性输出功能将加工轨迹用小段折线进行逼进,进后获取有限元分析所需的轨迹点,并根据进给速度与轨迹点的间距为工具头分配行至各轨迹点所需的时间,但应用此方法获取的轨迹点间距长短不一,数据相对杂乱,不易于对轨迹点进行检查与二次编辑,且无法从已有的NC代码中提取有限元分析所需的轨迹点。也有一些采用水平等距面切割模型的方法获取挤压工具运动路径轨迹点的研究[1-2]。
为了在数控渐进成形的有限元分析中准确地描述挤压工具的运动,研究一种从CAD/CAM软件输出的NC代码中提取有限元分析所需轨迹点的方法。
1 有限元分析所需轨迹点生成算法
板材数控渐进成形过程是一个比较复杂的非线性动载加工过程,当使用非线性动力显式分析软件对成形过程进行数值模拟时,加载空间曲线轨迹比较困难,需要将等高线轨迹离散成一系列的轨迹点,并将轨迹点的坐标x,y,z及对应的时间t分别以文本文档的格式保存,然后再利用ANSYS软件提供的数组读入功能,将各个轨迹点的坐标及时间读入到ANSYS中预先定义好的相应的数组中,从而完成对有限元仿真模型的加载。为此,通过VC++编程对NC代码文件进行读取,识别出NC代码中刀具轨迹的插补形式;然后,分别按照直线插补和圆弧插补两种插补形式,将刀具轨迹按给定的精度离散成点群,并将点的坐标连同设定的时间分别存储为有限元分析软件可读入的文本格式文件,整个算法过程如图1所示。

图1 算法流程
1.1 NC 代码读入
在NC代码中,关于描述刀具运动轨迹的命令有快速定位命令 (G00),直线插补命令 (G01)和圆弧插补命令 (G02,G03)。为此,需要读取G代码段中X,Y,Z后面的数据。文中利用VC++的“fopen”函数打开NC代码文件并进行顺序读取判断。当读取中遇到“G”字符时根据其后的两位字符判断刀具的运动类型 (快速定位命令、直线插补命令、圆弧插补命令),并利用“strchr()”函数对该命令符之后程序段中X,Y,Z字符后面的数据进行读取并分别存入字符数组中;同时根据刀具的运动类型对刀具轨迹进行离散处理,并利用“fprintf()”函数将离散点坐标写入文本文件中;然后继续顺序读取NC代码文件,直到遇到“null”结束读取过程。
1.2 基于离散的轨迹点生成
1.2.1 直线运动轨迹的离散
在NC代码的直线运动命令中,G00应用于挤压工具快速移动到距离下压点安全距离的位置和成形之后的退刀过程。由于此过程挤压工具不与板材接触,所以在有限元分析中无需对挤压工具在此过程中的移动轨迹进行离散处理,直接将代码段中设定的起点坐标和终点坐标分别存储到文本文件中。G01给出了直线运动的起点和终点,然而在渐进成形的有限元仿真过程中挤压工具运动的每一个轨迹点都要与相应的时间点一一对应,为了确保有限元仿真结果更加准确可靠,需要对直线运动轨迹按照所需要的长度间隔d进行离散处理,即在直线插补命令给出的直线运动的起点A(xA,yA,zA)与终点B(xB,yB,zB)之间添加若干个新点,确保两个相邻点之间的距离不大于间隔d。对于离散点Ki(xi,yi,zi),i=0,1,2,…,n,可根据公式 (1)和 (2)计算[13]:
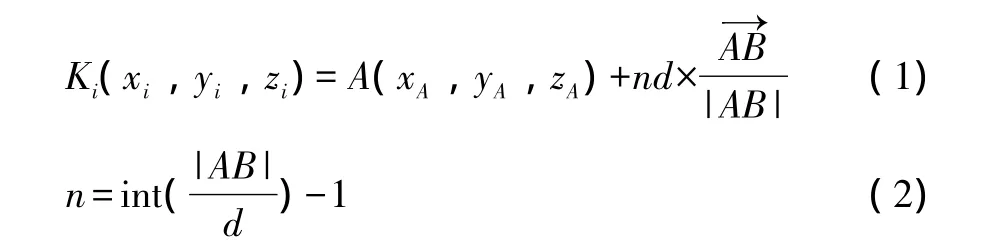
1.2.2 圆弧运动轨迹的离散
在NC代码中,G02和G03为圆弧运动命令,分别代表由起点顺时针和逆时针方向以R为半径到达终点的运动。当圆心角θ<180°时,R值取正号;当圆心角180°≤θ≤360°时,R值取负号。由于在CAM软件中,通常将圆心角180≤θ≤360°的圆弧曲线分割成若干个圆心角θ<180°的圆弧曲线,因此不考虑R取负值的情况。由于现今的有限元分析软件无法直接利用NC代码中给出的圆弧轨迹的起点、终点以及圆弧半径进行有限元分析,所以必须对圆弧轨迹进行离散处理生成有限元分析软件可读入的轨迹点。
在等高线轨迹的第i层xy平面内的圆弧插补命令中,起点A(xA,yA)、终点B(xB,yB)、顺时针方向圆心为O02(x02,y02)、逆时针方向圆心为O03(x03,y03)以及半径R,如图2所示,根据几何关系可得:
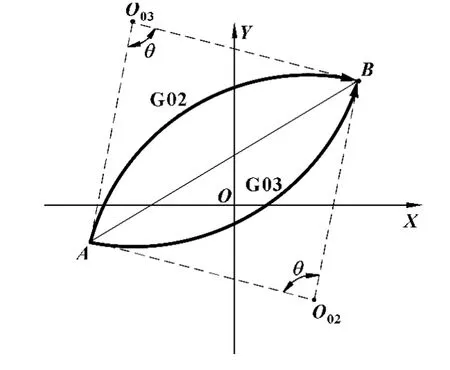
图2 圆弧插补

yk=kxk+b,其中b为直线截距,斜率

由式 (3)和 (4)解出圆心的坐标O02(x02,y02),O03(x03,y03)和直线的方程yk=kxk+b。以圆弧插补顺时针方向G02为例,通过起点A(xA,yA)和终点B(xB,yB)在XOY平面坐标系中的位置关系对圆心坐标O02(x02,y02),O03(x03,y03)进行选取。当xB>xA时如图3所示,若直线上的点Ki(xi,yi)中的坐标xi=xo且yi>yo,则O02(x02,y02)为该圆弧段的圆心,否则O03(x03,y03)为圆心。同理,当xB<xA时如图4所示,若xi=xo且yi<yo,则O02(x02,y02)为该圆弧段的圆心,否则O03(x03,y03)为圆心;当xB=xA且yA>yB时如图 5 所示,若yi=yo且xi>xo,则O02(x02,y02)为圆心,否则O03(x03,y03)为圆心;当xB=xA且yA<yB时如图6所示,若yi=yo且xi<xo,则O02(x02,y02)为圆心,否则O03(x03,y03)为圆心。应用上述方法,可求得圆弧插补逆时针方向G03在同样条件下的圆心坐标。
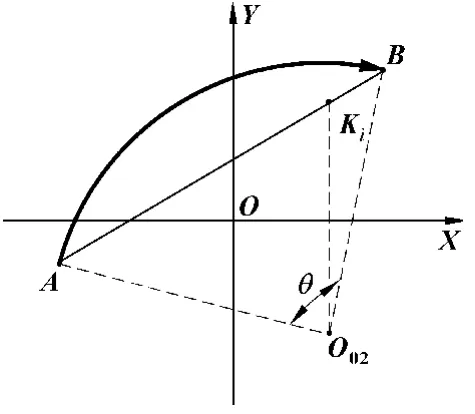
图 3 xB>xA

图 4 xB<xA

图 5 xB=xA且 yA>yB

图 6 xB=xA且 yA<yB
获取圆心坐标之后,需要将圆心角对应的圆弧进行离散处理,即在圆弧以离散精度φ'添加若干个新点,确保相邻两点之间的圆心角不大于φ',如图7所示。

图7 圆弧轨迹的离散

式中:m为A,B两点之间添加的离散点的数量。s为轨迹线间的离散分段数,由公式 (11)得到离散后离散点的数量m,如图8所示。以圆心Oo(xo,yo)为坐标原点 (其中o=02,03),坐标轴x和y分别平行于世界坐标系的X轴与Y轴建立相对坐标系,根据起点A(xA,yA)相对于圆心Oo(xo,yo)相对位置关系可以求得相对于x轴正方向的初始角φk(其中k=1,2,3,4)以及挤压工具在第i层XOY平面内运动轨迹的离散点的坐标Ki(xi,yi)。起点A(xA,yA)相对于圆心Oo(xo,yo)的相对位置关系如图8所示。

图8 起点A相对于圆心O的初始角度确定

2 算法应用实例
所提出的算法在Windows 7环境下,通过Visual C++平台和OpenGL图形库编程实现,并对“.txt”格式的NC代码文件进行读取,提取出离散后的挤压工具轨迹点信息。如图9所示为需要进行有限元分析的板材件模型;图10所示为利用UG生成的成形轨迹和NC代码文件;图11所示为从NC代码提取并经离散化处理得到的成形轨迹点和以文本文件存储的轨迹点的x,y,z坐标;如图12所示为利用图11所示轨迹点加载的基于ANSYS/LS-DYNA的数控渐进成形有限元分析结果。

图9 实例模型

图10 基于UG的成形轨迹与NC代码

图11 离散化的轨迹与保存在文本文件中的点

图12 有限元分析
3 结论
研究一种从CAD/CAM软件输出的NC代码中获取板材数控渐进成形有限元仿真所需的挤压工具运动轨迹离散点信息的方法。该方法能够根据给定的离散精度将直线运动轨迹和圆弧运动轨迹离散为点群并将点的坐标自保存到文本文件中,所提取的轨迹离散点可应用于数控渐进成形过程的有限元分析仿真,这使基于NC代码的数控渐进成形的有限元分析成为可能,为更复杂形状板材件的数控渐进成形有限元分析提供了一个途径。
[1]MICARI F,AMBROGIO G,FILICE L.Shape and Dimensional Accuracy in Single Point Incremental Forming:State of the Art and Future Trends[J].Journal of Materials Processing Technology,2007,191:390-395.
[2]崔震,高霖,陆启建.复杂钣金零件渐进成形方法[J].机械工程学报,2007,43(12):235-239.
[3]LI Le,SEO Young-ho,HEO Seong-chan,KANG Beom-soo,et al.Numerical Simulations on Reducing the Unloading Springback with Multi-step Multi-point Forming Technology[J].The International Journal of Advanced Manufacturing Technology,2010,48(1-4):45-61.
[4]YAMASHITA M,GOTOH M,ATSUMI S.Numerical Simulation of Incremental Forming of Sheet Metal[J].Journal of Materials Processing Technology,2008,199(1):163-172.
[5]TISZA M,PANITY I,KOVÁCS P Z.Experimental and Numerical Study of a Milling Machine-based Dieless Incremental Sheet Forming[J].International Journal of Material Forming,2010,3(1):971-974.
[6]TEKKAYA A E,SHANKAR R,SEBASTIANI G,et al.Surface Reconstruction for Incremental Forming[J].Production Engineering,2007,1(1):71-78.
[7]蒋松,高锦张,贾俐俐.板料多道次渐进成形下沉现象的模拟分析[J].锻压技术,2010,35(2):50-54.
[8]沈黎萍,高锦张,蒋松,等.板料渐进成形半球形件的路径研究[J].锻压技术,2010,35(6):40-44.
[9]李珑杲,高霖,韦红余.金属板材数控渐进成形有限元仿真过程中复杂成形路径的构建方法[J].机械工程学报,2006,42(6),227-230.
[10]李磊,周晚林,刘成丹,等.金属板材单点无模渐进成形数值模拟及分析[J].南京航空航天大学学报,2009,10(5),611-614.
[11]史晓帆 ,高霖,徐岩.基于数控编程的渐进成形模拟复杂刀路构建方法[J],航空制造技术,2012,12,91-93.
[12]ZHU Hu,LI Nan,LIU Zhijun.The Effect of Pressing Direction on the 5-axis CNC Incremental Forming Quality[J].International Journal of Material Forming,2012,5(3):227-233.
[13]林雯雯,数控渐进反向成形CAD/CAM系统研究[D].沈阳:沈阳航空航天大学,2013.

