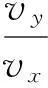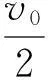对2012高考上海卷12题的分析与拓展
对2012高考上海卷12题的分析与拓展
王修权
(甘肃省永昌县第一高级中学,甘肃永昌737200)
题目(2012高考上海卷)如图1所示,斜面上a、b、c三点等距,小球从a点正上方O点抛出,做初速为v0的平抛运动,恰落在b点.若小球初速变为v,其落点位于c,则().

图1
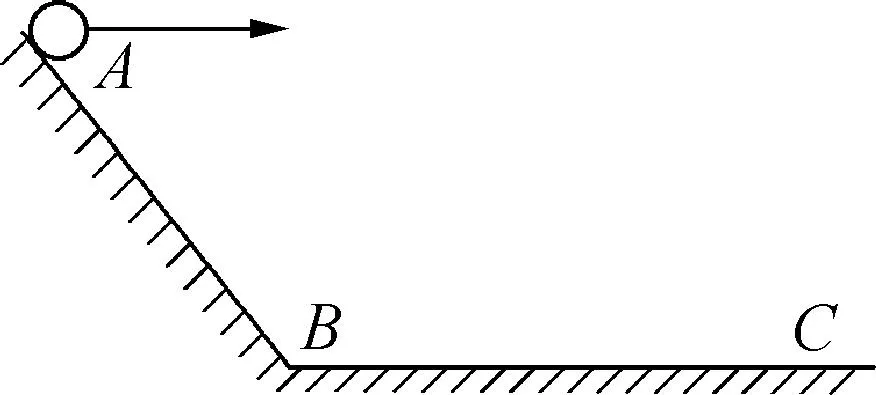
A.v0 B.v0=2v0 C. 2v0 D.v>3v0 分析:该问题显然属于与平抛运动相关的问题,解决该问题的关键点在于分清两次小球平抛运动的物理参量之间的关系.根据题目条件,很容易确定两次平抛运动小球落在斜面上时水平方向上的位移后者是前者的两倍.我们可以用不同的方法去求解. 解法1:利用平抛运动的规律 解法2:极限法1 为此,要满足题目中两次平抛运动落在斜面上时水平方向上的位移后者是前者的两倍关系,抛出速度只有A选项符合条件. 解法3:极限法2 将题目中的斜面改为平面,则两次平抛运动小球在空中运动的时间相等,要满足题目中两次平抛运动水平方向上的位移后者是前者的两倍关系,只能是后者的平抛初速度是前者的2倍,结合题目中的实际情景是一斜面,定性分析可知,后者在空中运动的时间要比前者长,要满足题目条件,抛出速度只有A选项符合条件. 图2 A.b点B.b、c之间 C.a、b之间D. 无法判断 解析:过c点作水平面,小球落到水平面的水平位移是小球以初速度v0抛出时的一半,延长小球运动的轨迹线,得到小球应该落在b、c之间,B项正确. 原题拓展2:如图3所示,AB为斜面,BC为水平面,从A点以水平速度v0抛出一小球,其落点到A的水平距离为x1;从A点以水平速度2v0抛出小球,其落点到A的水平距离为x2,不计空气阻力,则x1∶x2可能等于(). A. 1∶2B. 1∶3 C. 1∶4D. 2∶3 图3 解析:球落地情况有三种:一是都落在斜面上;二是都落在水平面上;三是一次落在斜面上,另一次落在水平面上.对第一、二两种情况,根据原题不难算出x1∶x2分别为1∶4和1∶2.对第三种情况,如图4所示,根据平抛运动的规律,若撤掉斜面,都落到平面上,则x1将变大,x1∶x2将变为1∶2,故现在比值一定小于1∶2;若撤去水平面,让斜面延伸,两球均落在斜面上,则x2将变大,x1∶x2将为1∶4,故现在x1∶x2一定大于1∶4,只要在1∶4到1∶2的比值都是可能的,正确答案为A、B、C. 图4 小结:斜面上的平抛运动每年高考几乎都要考,要求考生必须掌握其相关知识点.此外,通过一题多解,一题多问,多题归一,可以起到事半功倍的作用.