蝴蝶形钢板墙的抗侧刚度和承载力研究

马磊，李启才

（1.苏州科技学院土木工程学院，江苏苏州215011；2.江苏省结构工程重点实验室，江苏苏州215011）

蝴蝶形钢板墙的抗侧刚度和承载力研究

马磊1，2，李启才1，2

（1.苏州科技学院土木工程学院，江苏苏州215011；2.江苏省结构工程重点实验室，江苏苏州215011）

在带缝钢板剪力墙的基础上进行改进，提出了一种新型的蝴蝶形钢板墙，拟用于自复位钢框架中作为主体耗能构件。借鉴带缝钢板墙的分析方法，推导了蝴蝶形钢板墙的初始刚度及承载力理论计算公式。为验证理论计算公式的正确性，深入了解蝴蝶形钢板墙的受力性能，设计了3组不同尺寸的试件，并进行有限元分析。结果表明：理论公式计算与有限元结果符合良好；蝴蝶形钢板墙有着比带缝钢板墙更好的抗震耗能性能，控制蝴蝶杆的宽厚比b/t不超过10可以保证钢板墙良好的延性及耗能性能；试件在层间位移角大约为0.5%时即进入塑性耗能，在地震中将先于主体结构进入塑性，作为耗能构件有效地减轻了主要结构的损坏。

蝴蝶形钢板墙；抗震耗能性能；初始刚度；极限承载力

基于性能的抗震设计中，结构的“残余变形”和“最大变形”都是控制结构性能的重要指标。自复位钢框架结构由于能较好地控制结构的残余变形，在近年来得到了研究者们广泛的关注。在自复位框架结构中，主要构件需要保持弹性而不具有耗能能力，地震输入结构的能量需靠附加的耗能装置来吸收。当前的研究文献主要通过在梁柱节点安装角钢[1]、摩擦耗能钢板[2]或在自复位框架中內填薄钢板[3]来增加框架的耗能，该文研究一种连接于自复位框架上、下梁之间的蝴蝶形钢板墙，如图1所示，在多遇地震下作为结构的抗侧力构件，在设计地震和罕遇震下率先进入塑性，作为耗能构件吸收地震输入的能量，有效保护主体结构免受损坏。

蝴蝶形钢板墙是带缝钢板剪力墙[4]的一种改进形式。带缝钢板墙具有较高的延性和耗能能力，在多遇地震作用下，其能够在位移较小的情况下参与抵抗部分地震作用；在罕遇地震作用下，作为主要耗能构件，吸收输入结构的地震能量[5]。然而，带缝钢板墙的塑性变形耗能主要集中于缝间弯曲杆的两端，且已有的带缝钢板墙试验[4，6-7]都出现了钢板的疲劳撕裂破坏，钢板墙耗能能力发挥不充分。Kobori等[8]通过在钢板上开设蜂窝孔，形成蜂窝状钢板耗能器，如图2所示，耗能段的几何形状贴近于两端固定双曲率弯曲变形梁的弯矩图分布，可以使屈服范围分布更长，耗能能力更好。Ma Xiang等[9]对类似蜂窝状耗能器的蝴蝶形钢板耗能器做了系统的试验研究，并与开缝钢板耗能器进行了对比，结果表明，前者的抵抗屈曲能力和抗疲劳撕裂破坏能力都要优于后者。

文中研究的蝴蝶形钢板墙，主要由三部分组成，即水平连续板带、弯曲杆、加劲肋。水平连续板带包括上板带、中板带和下板带，弯曲杆包括蝴蝶杆和矩形杆，加劲肋包括边缘钢管加劲和水平横向加劲。蝴蝶形钢板墙通过螺栓直接和自复位框架梁进行连接，震后方便更换。本文将首先分析蝴蝶形钢板墙的受力机理，提出蝴蝶形钢板墙的刚度和承载力计算公式，然后通过对不同几何尺寸蝴蝶形钢板墙的有限元数值模拟分析，印证前述机理分析和理论公式的正确性。

图1 蝴蝶形钢板墙示意图

图2 蜂窝状钢板耗能器[8]

1 蝴蝶形钢板墙的理论分析

1.1 蝴蝶杆的受力分析

蝴蝶形钢板墙的整体受力性能等同带缝钢板剪力墙，孔间蝴蝶杆在不发生面外失稳的条件下，其受力类似于两端固定的弯曲梁。图3给出了蝴蝶杆在水平剪力Q作用下的内力图，按文献[9]对此类变化截面高度双曲率受弯梁所作的推导，某坐标为x的截面外围纤维应力

式中，t为蝴蝶杆的厚度，L为蝴蝶杆的长度，I（x）为x处的截面惯性矩，其他符号的含义见图3，令dσ/dx=0，可以求得xm=[a/（b-a）]·（L/2），外围纤维应力的极大值

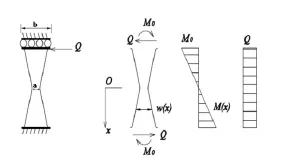
图3 蝴蝶杆的受力状态及内力分布

当截面边缘开始屈服时，蝴蝶杆承受的弯矩和水平剪力的大小可以通过令σmax=σy，求得

一旦某一截面率先进入屈服，随着侧向力的增加，其紧邻截面将相继进入屈服。当率先屈服的截面形成塑性铰时，蝴蝶杆达到其极限承载力，对于矩形截面，极限承载力可按下式计算：

在文献[9]中，取a=b/3，得到xm=L/4，即在离杆端L/4距离的截面最先屈服并形成塑性铰。考虑到截面削弱将不利于稳定，取a=2b/5，则得xm=L/3，即离杆端L/6距离的截面最先屈服并形成塑性铰，这样截面削弱能够得到改善，稳定性能得到提升。计算变截面梁的稳定，如果按不变截面计算，并以其小端截面尺寸为准将偏于保守。蝴蝶杆的稳定计算可以等效为一端固定，另一端自由，长度为L/2的悬臂梁承受端部集中荷载Q，若按承受集中荷载的较小端计算，文献[10]有，其中Iy=at3/12、It=at3/3，E、G分别为材料的杨氏模量和剪切模量。因此若a取2b/5比取b/3将提高20%的稳定承载力。

蝴蝶杆在单位水平力作用下的位移可以通过单位荷载法求得

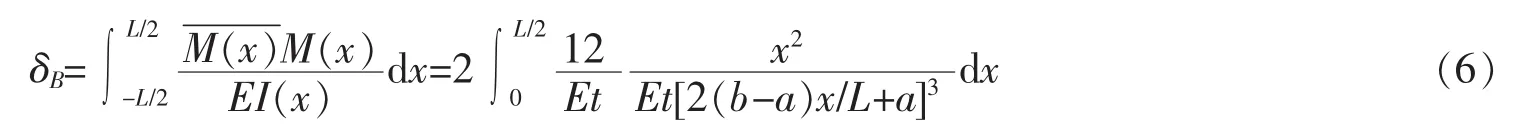
利用Matlab可以进一步得到

1.2 蝴蝶形钢板墙整体受力分析

蝴蝶形钢板墙的整体受力性能等同带缝钢板剪力墙，墙板在水平荷载作用下的变形形式介于整体剪切变形和弯曲变形之间，其变形主要由三部分组成：水平连续板带的剪切变形、弯曲杆的剪切变形以及弯曲杆的弯曲变形。通过边缘竖向钢管加劲及横向水平加劲，可以在很大程度上避免整板的面外屈曲，亦可通过控制蝴蝶杆的宽厚比来控制其弯扭屈曲，防止钢板墙过早失稳而丧失承载力，确保构件的延性破坏模式。文献[11]对帯缝钢板剪力墙提出“先塑性后屈曲”的设计前提，同样适用于蝴蝶形钢板墙。下面假定在屈服前钢板墙不发生屈曲或者屈曲很小，基本不影响钢板面内受力行为的前提下，借鉴文献[12]对带缝钢板墙的分析，对蝴蝶形钢板墙的初始刚度和极限承载力的理论计算进行推导。

1.2.1 弹性初始刚度

（1）水平连续板带剪切变形。假定板带在荷载作用下不发生屈曲，板带将以剪切变形为主。忽略板带受弯引起的变形，这样板带对墙板整体柔度的贡献为

式中，κ为截面剪切形状系数，对于矩形截面，可取1.2；B为钢板墙的总宽度；t为钢板墙厚度；H为钢板墙总高度；m为弯曲杆排数，在图1中为2；L为蝴蝶杆长。

（2）弯曲杆剪切变形。弯曲杆以受弯为主，同时也受剪，存在剪切变形，弯曲杆的剪切变形对墙板的贡献可以采用如下公式进行计算

式中，n为每排弯曲杆根数，b为弯曲杆杆端宽度，其他符号含义同前。

（3）弯曲杆弯曲变形。弯曲杆相当于一端固定，另一端滑动的梁，在端部横向水平荷载作用下发生弯曲变形。对于两端的矩形杆件在单位力作用下的弯曲变形，按单位荷载法，可按下式计算

蝴蝶杆在单位力作用下的弯曲变形，由1.1节的推导式（7），按如下公式计算

m×n根弯曲杆，其中2×m根矩形杆、（n-2）×m根蝴蝶杆，先并联再串联，因此，所有弯曲杆弯曲变形对墙板的总的柔度贡献为

在式（10）、（11）中，假定弯曲杆两端固结，事实上，弯曲杆受到上下板带的有限约束，并非完全固结，所以在杆件变形的计算中，应引入修正系数，以考虑约束边界条件的影响。参考文献[2]对于帯缝钢板墙提出的修正方法，考虑到蝴蝶形钢板墙中的应力集中没有带缝钢板剪力墙那么严重，对上式（12）引入修正系数k（α），k（α）=1+α-1，其中α=L/b，则式（12）成为

叠加三部分变形，得到墙板在单位荷载作用下总的变形量，即墙板的柔度。墙板的弹性初始刚度

1.2.2 极限承载力

从上面对初始刚度的推导可以看出，总刚度的贡献并没有包含边缘冷弯加劲方钢管的贡献，这是因为加劲方钢管的两端没有边界约束，在受载前期基本不参与或很少参与受力。而水平横向加劲肋由于其方向与受力方向平行，对弹性初始刚度也几乎没有贡献。但边缘加劲方钢管在其纵向是和墙板相连的，墙板在一定程度上可以起到加劲钢管的边界约束作用，随着弯曲杆进入塑性，边缘竖向加劲方钢管也将逐渐参与到墙板受力，与外围矩形杆一起组成组合截面，如图4所示，参与钢板承载。实际上，对于边缘竖向钢板加劲的帯缝钢板剪力墙的极限承载力计算，文献[13]就曾建议考虑边缘加劲肋对承载力的贡献，按加劲钢板与最外围矩形弯曲杆一起组合形成的T形构件来计算，这样得出的结果与试验符合得更好。

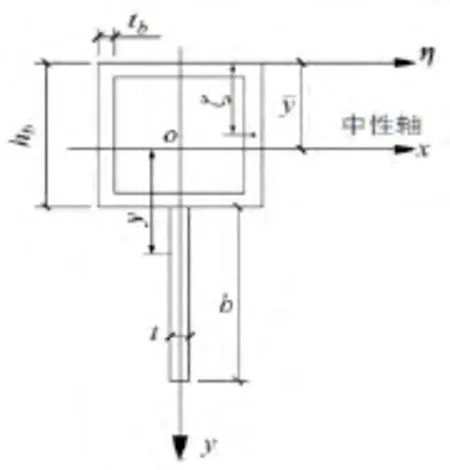
图4 组合截面

参见图4，组合截面的中性轴位置，即几何中心可由下式计算

式中，ζ为截面某点到图示轴的距离，A为整个组合截面的截面面积，进而可按下式求得塑性截面系数

式中，y为截面某点到x轴的距离，则截面的极限弯矩

当蝴蝶杆完全形成塑性铰时，墙板达到其极限承载力，综合考虑蝴蝶形杆及组合截面的承载力可得

上式中，右端第一项代表边缘组合截面的抵抗贡献，它相当于只考虑了1/2的塑性弯矩，在这里由于加劲方管两端没有边界约束，形成全塑性截面不符合实际，因而在计算中取其一半值，从后面的有限元分析看，这样做是合理的；后一项代表蝴蝶杆的贡献，共n-2根，由式（5）而来。

2 有限元模拟验证

为了进一步研究蝴蝶形钢板墙的受力性能并印证上述理论推导的正确性，设计了3组共15个试件，应用ANSYS软件对试件进行有限元数值模拟分析。

2.1 有限元试件

试件的高均取为2 100 mm，缝宽取为12 mm，蝴蝶杆的a/b取值为0.4，这样理论上离端部L/6距离的截面将率先屈服。中间板带的高度统一取300 mm，试件边缘竖向加劲采用截面尺寸100 mm×100 mm×10 mm的冷弯方管，横向水平加劲宽度为50 mm，厚度同钢板墙厚，正背面都设。采用横向水平加劲主要是考虑到蝴蝶形钢板墙削弱比带缝钢板墙严重，钢板的整体面外屈曲不易保证。试件按如下方式命名：第一个字母代表有限元试验的类别，A代表第一类试件，其整体高宽比为1∶1；B代表第二类试件，其整体高宽比约为2∶1。字母接着的两个数字代表蝴蝶杆的宽厚比（b/t），第三个数字代表蝴蝶杆的长宽比（L/b），第四个数字代表弯曲杆排数（m）。例如试件A1062即代表整体高宽比为1∶1，弯曲杆排数为2层，宽厚比和长宽比分别为10和6的试件。C类试件开孔几何参数与A类相同，但钢板厚度增加到16 mm，其命名为在与其相应的A类试件名称前加字母C。各试件的具体几何参数见表1与表2。

试件的底部边界约束所有自由度，上部边界约束除UX外的所有自由度，并耦合UX。在耦合的主节点上施加UX方向的位移荷载，按一阶屈曲模态施加1‰的初始几何缺陷。材料本构关系采用理想弹塑性模型，屈服强度取235 MPa，按位移加载，最大位移角取4%。

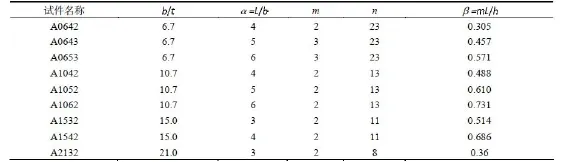
表1 A类试件的相关参数

表2 B、C类试件的相关参数表

图5 试件在2%层间位移角下的应力、应变云图

2.2 有限元分析

图5（a）给出了典型试件A1042在层间位移角为2%时的Von-Mises应力云图，蝴蝶杆大部分都进入屈服，杆中间为反弯点，因此杆中间的一小段区域内应力很小，仍保持弹性。图5（b）给出了局部区域蝴蝶杆的总应变分布，塑性铰大约出现在离杆端L/6处截面，与理论分析一致。为方便与带缝钢板墙比较，图5（c）给出与A1042对应的带缝钢板墙在层间位移角2%时的Von-Mises应力分布云图，屈服应力集中于矩形杆的端部，钢板墙屈服的面积较小。按文献[9]的理论，形成塑性铰的位置易于变形集中，截面的两边有不同曲率时易于应力集中。对于带缝钢板墙的弯曲杆，这两种情况叠加在一起，非常不利，几乎所有的带缝钢板墙试验都出现了弯曲杆的疲劳撕裂破坏[4，6-7]。蝴蝶形钢板墙中的蝴蝶杆塑性铰截面与杆端截面相隔一定距离，能有效地避免两种不利情况的叠加，疲劳破坏得到改善。

图6给出了本蝴蝶形钢板墙试件A1052在位移加载到4%后卸载到零时的面外变形图，蝴蝶形钢板墙由于附加了横向水平加劲板，其失稳形式表现为蝴蝶杆的弯扭屈曲。蝴蝶杆的弯扭屈曲是导致试件承载力降低的主要原因，但在保证一定宽厚比的前提下，屈曲大多都是发生在屈服之后，保证了耗能能力的发挥，见图7（a）。从图7（a）和图7（b）对比来看，整体高宽比增大到2∶1，对试件的延性稳定性能影响很小，它们的滞回曲线高度类似。如图7（c）所示，C类试件宽厚比大于A类，其滞回曲线要相对稳定饱满，稳定性增强。与同类型研究得出的结论一样[6，9]，有限元分析表明蝴蝶杆的宽厚比是影响钢板性能的主要因素，当宽厚比超过15时，滞回曲线呈现出明显的剪切滑移特征并伴有少量的捏缩，如图7（d）所示，这是蝴蝶杆的弯扭屈曲造成的。所有试件在层间位移大约为0.5%时即进入塑性，地震来时蝴蝶形钢板墙将率先进入屈服耗能，减轻主要结构构件的损坏。

图6 A1052面外（UZ）变形图

图7 试件的滞回曲线

表3给出了有限元模拟试件的承载力、刚度与理论计算结果的对比及误差分析。总体来看，理论公式与数值分析非常近似。对于承载力，绝大多数试件理论值的误差不超过10%，最大不超过20%，有限元和理论计算比值的平均值为0.946，方差为0.076；对于刚度，绝大多数试件理论值的误差不超过10%，最大不超过20%，有限元和理论计算比值的平均值为1.049，方差为0.064。

表3 试件的承载力与刚度

承载力的理论值总体偏大。理论计算公式是在蝴蝶杆形成塑性铰之前不发生屈曲或者屈曲很小的前提下推导的，并且直接考虑了边缘加劲钢管与弯曲杆组合截面一半的塑性强度。对于第一个前提，一般通过加劲和控制蝴蝶杆的宽厚比，很容易满足；而直接考虑边缘加劲钢管与弯曲杆组合截面一半的塑性强度，有着主观臆断的因素，实际上，对于有些试件如A2132，图8给出了其在最大承载力时的面外变形图和Von-Mises应力分布云图，试件在最大承载力时的面外变形并不严重，最大仅为14.8 mm，蝴蝶杆屈服程度也较高，但边缘加劲钢管的应力却基本不到50 MPa，这说明边缘加劲肋参与受力的程度并不高，比公式假设的50%要低许多，造成了理论计算值偏大。事实上，每个试件的边缘加劲钢管参与受力的程度都不一样，想要精确分析会非常困难。从总体来看，本文的考虑方法还是比较可靠的，分析计算也简单。

图8 A2132的面外变形云图和应力云图

刚度的理论计算值总体偏小。引起刚度公式误差的原因主要有两个：一是修正系数，其表达式主要借鉴文献[6]对带缝钢板墙刚度所做的修正，其本身就带有一定的不确定性；二是理论公式没能考虑墙板的初始面外变形。

3 结论

为使带缝钢板墙的耗能性能得到更好地发挥，本文对其形式进行改进，形成发展了蝴蝶形钢板墙。在理论分析的基础上，推导了蝴蝶形钢板墙的承载力与刚度计算公式，并设计了三组蝴蝶形钢板墙试件，通过对试件进行有限元分析，得到如下结论：

（1）证实了蝴蝶杆的屈服应力分布模式，其屈服范围比带缝钢板墙更广。

（2）通过选择蝴蝶杆的a/b值，可以控制形成塑性铰的位置，使其离开蝴蝶杆端部，增强了钢板墙的抗疲劳撕裂破坏能力。

（3）蝴蝶形钢板墙的失稳模式为蝴蝶杆的弯扭屈曲。

（4）蝴蝶杆的宽厚比不超过10时，蝴蝶形钢板墙的滞回曲线相对稳定饱满，表现出良好的延性耗能性能，是一种良好的耗能构件。

（5）试件在层间位移角为0.5%时即进入塑性耗能，在地震中可以先于主体结构进入塑性，作为主体耗能构件，较好地减轻了主体结构的损坏。

（6）整体上理论公式计算与有限元模拟吻合较好，说明理论公式有较高的可靠性。

[1]Ricles J，Saues R，Garlock M，et al.Posttensioned seismic-resistant connections for steel frames[J].J Struct Eng，2001，127（2）：113-121.

[2]Christopoulos Constantin，Filiatrault Andre，Uang Chia-Ming，et al.Posttensioned energy disspating connections for moment-resisting steel frames[J].J Struct Eng，2002，128（9）：1111-1120.

[3]Clayton Patricia M，Winkley T B,Berman J W,et al.Experimental investigation of self-centering steel plate shear walls[J].J Struct Eng，2012，138（7）：952-960.

[4]蒋路，陈以一，卞宗舒.足尺帯缝钢板剪力墙低周往复加载试验研究Ⅱ[J].建筑结构学报，2009，30（5）：65-71.

[5]陈以一，宁燕琪，蒋璐.框架-带缝钢板剪力墙抗震性能试验研究[J].建筑结构学报，2012，33（7）：133-139.

[6]Hitaka T，Matsui C.Experimental study on steel shear wall with slits[J].Journal of Structural Engineering，2003,129（5）：586-595.

[7]赵作周，肖明，钱稼如，等.开缝钢板墙抗震性能的试验研究[J].建筑结构，2007，37（12）：105-109.

[8]Kobori T,Miura Y,Fukusawa E,et al.Development and application of hysteresis steel dampers[C]//Proc.11thWorld conference on Earthquake En-gineering，1992．

[9]Ma Xiang，Eric Borchers，Alex Pena，et al．Design and Behavior of Steel Shear Plates with Openings as Energy Dissipating Fuses[R]．Stanford University,USA,2011．

[10]Timoshenko S,Gere J M．Theory of elastic stability[M]．2ndEd．McGraw-Hill,New York,USA,1961．

[11]陈以一，蒋路．帯缝钢板剪力墙的承载力和开缝参数研究[J]．建筑科学与工程学报，2010，27（3）：109-114．

[12]孙飞飞，王文涛，刘桂然．开缝钢板剪力墙的理论分析与数值模拟[J]．建筑钢结构进展，2011，5（13）：37-43．

[13]Gustavo Cortes．Steel slit panel frames of lateral resistance of building[D]．Purdue University,West Lafayette,Indina,USA,2009．

Initial stiffness and bearing capacity of the butterfly-shaped steel plate walls

MA Lei,LI Qicai
（School of Civil engineering,SUST,Suzhou 215011,China）

A new butterfly-shaped steel plate wall was proposed on the basis of steel plate shear wall with slits so as to improve the energy dissipation capacity of self-centering steel moment-resisting frames．In the light of steel plate shear walls with slits,the initial stiffness and bearing capacity theory formula of butterfly-shaped steel plate wall were proposed．To better understand the mechanical properties of the wall and verify the correctness of the theoretical formula,three groups of samples were designed,and a series of finite analysis were conducted．The result showed that the theoretical formula greatly matched the result from the finite element analysis,and that the seismic energy performance of butterfly-shaped steel plate walls surpassed the steel plate shear wall with slits; when the width-to-thickness ratios(b/t)of the butterfly links were less than 10,the wall showed good ductility and energy dissipation;when the drift was about 0．5%,butterfly-shaped steel plate walls were totally yielded, which would precede the main structure into plastic,reducing the damage to the main structures in the earthquake;the proposed theoretical calculation formulas can give reasonable estimation of finite element analysis results．

Butterfly-shaped steel plate walls；seismic energy dissipating；initial stiffness；ultimate bearing capacity

TU391

A

1672-0679（2015）01-0030-07

（责任编辑：秦中悦）

2014－04-17

国家自然科学基金项目（51378326）；江苏省结构工程重点实验室开放课题（ZD1204）

马磊（1987-），男，湖南邵阳人，硕士研究生。