基于能量的钢结构抗震性态设计研究进展

顾强，孙国华

（苏州科技学院土木工程学院，江苏苏州215011）

基于能量的钢结构抗震性态设计研究进展

顾强，孙国华

（苏州科技学院土木工程学院，江苏苏州215011）

基于性态的抗震设计理念已被普遍接受，我国《建筑抗震设计规范》已纳入性态设计的内容，但因研究成果、技术储备的不足，目前各国规范还都未能提出一般性的设计方法，显现出在此领域进行科学研究，提出基于结构性态实用设计方法的急迫性。文章综述了钢结构基于能量抗震设计方法的研究进展及存在的问题。

钢结构；滞回能；性态；抗震设计

现行的建筑抗震设计采用基于强度的弹性设计方法，用两种手段计算结构设计地震作用：（1）对质量、刚度规则分布的结构用等效静力法，根据结构延性及超强，用结构反应修正系数对设防地震弹性反应谱进行折减得到设计地震作用，将按一定模式分布的等效侧向静力地震作用与重力荷载组合作为结构的强度需求；（2）基于弹性动力分析得到结构的设计地震力分布，与重力荷载组合后作用于结构，此方法考虑了结构的动力特性，可用于任意结构。然后，基于结构强度不小于强度需求的原则按弹性设计结构（我国称为小震弹性设计法），并控制结构在设防地震（中震）下的侧移（我国规范控制小震和大震侧移）。

现行规范的设计地震作用远低于设防地震下结构遭受的实际地震作用，规范指定的设计地震力并不是要使结构在设防地震下无损伤，而是指定一个最小侧向抗力水准，并期望如此设计的结构在设防地震下进入弹塑性状态（结构出现轻微破坏，可修），用非直接方式考虑结构强震下的弹塑性。此方法简单、易掌握，但对结构的非弹性性能没有提供足够的信息，对结构遭受大震作用时仅通过验算最大层间变形避免出现薄弱层，无法保证结构进入弹塑性阶段出现理想的破坏模式，也无法区别不同结构体系滞回耗能的影响，对设防地震及罕遇地震（大震）下结构的性态（如应力，变形，结构件及非结构件的损毁程度，结构破坏模式、倒塌概率等）是无法明确控制的。近年来，按现行抗震规范设计的部分建筑遭受了超过设防水准的强震，结构的损毁程度、丧失使用功能引起的经济损失之大、修复成本之高超出预想，迫使工程界对现行抗震设计理论和方法进行了深刻的反思，探讨更完善的结构抗震设计理论及方法。

美国学者提出的基于性态抗震设计理念致力于明确控制结构在不同强度地震下的性态，对应不同强度的地震建立不同的结构性态水准和性态指标；对预期强度的地震，结构破坏不超过特定的性态，并具有期望水准的可靠度。基于性态的抗震设计理念已被普遍接受，部分国家的建筑抗震设计规范正在发生根本性的变化，我国《建筑抗震设计规范》GB50011-2010已纳入结构性态设计的内容，第3.10节（建筑抗震性能化设计）已初步建议了地震动水准及一些宏观要求，其附录M也列出了一些初步建议供参考。因研究成果、技术储备的不足，目前各国规范还都未能提出一般性的性态设计方法，显现出在此领域进行科学研究的急迫性。

基于性态的结构抗震设计理论及方法为21世纪土木工程学科的重要研究方向，各国学者提出了不同的设计方法，可归类为基于强度方法、基于位移方法、基于能量方法、基于损伤方法等。基于强度方法不能考虑强震持时对结构损伤的影响。基于位移方法间接考虑了结构非弹性变形的能量耗散，其局限性在于只考虑了结构的最大反应。而基于能量的设计方法涉及了力和位移两个参数，还可反映地震持时的影响。研究表明地震输入能量是表征地震动破坏能力最为合理的指标，可以通过等效单自由度结构来获取多自由度结构的输入能量。基于能量的设计方法有概念明确、形式简单的优点，能够较好地反映地震动的强度、频谱特性、强震持时对结构引起的损伤破坏。

尽管基于能量的抗震设计思想自Housner于1956年提出以来获得了持续的关注和研究，但目前对其应用仍处于发展阶段，如何计算结构的地震动能量需求及基于能量的一般性设计方法是是各国学者所面临的主要挑战。

1 地震动输入能量

承受底部激励的单自由度体系能量方程为

方程（1）左边第一项为动能，第二项为阻尼能，第三项为弹性应变能加滞回能。方程右边项为输入能。如果方程（1）采用绝对位移，得到的能量为绝对能量；如果采用相对位移，得到的能量称为相对能量。绝对能量与相对能量的差别只限于动能项和输入能项，而且差别是较小的。上述区分不影响与设计相关的滞回能项。动能项是由于结构移动惯性力产生的能量，阻尼能等于阻尼力乘以每个时间步的位移，输入能等于底部剪力乘以地面位移。输入能为方程左边四项能量之和，它比峰值地面加速度或谱强度更好地反映了地面运动的特征，因为它同时包含了地面运动特征和结构的性能。地震对结构的作用从本质上讲是一种能量的传递、转化与耗散的过程。当地震动输入给结构的能量小于结构的耗能能力时,结构是安全的，反之结构将受到破坏。地震对结构的影响可作为能量输入－结构特性和地面运动特征的函数，结构的能力定义为能量耗散能力，抗震设计成为地震能量输入和结构能量耗散能力的平衡。方程（1）左边的四项能量可分为两组：动能加应变能为建筑储存能量，阻尼能加滞回能为建筑耗散能量，即建筑储存的能量加耗散的能量等于总的输入能。动能和阻尼能不是明确地由结构抵抗，阻尼能由建筑的部件产生，如房间的隔断、连接的滑动等，可衰减自由振动。这两项能量与构件截面尺寸无关，结构不储存也不耗散它们。研究结果表明动能和应变能都很小，几乎可以忽略，这两项在基于能量的设计中是没有意义的，阻尼能和滞回能构成了输入能量的主体。与结构设计有关的主要能量项是滞回能，滞回能的研究是能量分析方法研究的核心内容。滞回能与结构震害关系的研究包含两方面的内容,分别是累积滞回能和瞬时滞回能的研究，前者与结构的累积损伤相关,后者则决定了结构的最大位移反应，结构的累积损伤破坏与最大位移破坏均能用能量方法解释。

Chou&Uang[1]认为实现结构基于能量抗震设计、评估的前提是根据地面运动特征，如震级、震中距、场地类别建立结构的能量需求。建立非弹性单自由度体系吸收能量谱形式的抗震需求可作为发展基于能量抗震设计和评估的第一步。文中将结构吸收能Ea（由可恢复的弹性应变能和不可恢复的滞回能Eh组成）作为能量需求指标是因为它不仅与结构屈服强度相关，而且直接与结构破坏相关。将Ea用等效速度，m为质量）表示。当结构反应为弹性时，Va等于拟速度V，用Va在基于能量设计方法抗震需求和基于强度设计方法抗震需求之间建立了联系。文献[1]根据加利福尼亚的273个强震记录，用衰减模型（attenuation approach）和二阶段回归分析将Va表示为震级、震中距、场地类别的函数，得出的Va谱显示出与拟速度V谱有相似的形状，场地类别对它的影响较大。文中指出所提出的吸收能量谱会明显低估近场地震的能量需求，近场地震的能量需求尚需进一步研究。

McKevitt，et al[2]分析了几个多层建筑在地震激励下的滞回能谱，指出当刚度和强度沿结构高度均匀分布时，结构的最底层耗散了大部分的滞回能，预知滞回能在结构内的分布将奠定基于能量设计方法的基础。Khashaee[3]分析了场地和地面运动特征对地震输入能、滞回能及在结构内分布的影响,表明场地和地面运动特征对传递到结构的能量有较大影响，但对能量沿结构高度的分布影响很小，结构体系对能量大小及分布有影响。文中提出了地震输入能和滞回能谱的表达式。地震相对输入能计算式为

滞回能计算式为

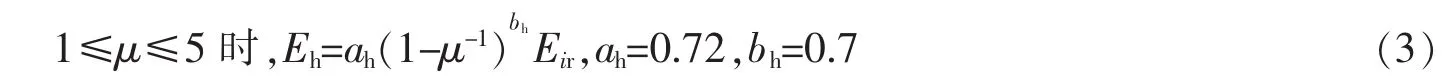
Chou,Uang[4]采用等效单自由度（ESDOF）体系预测多自由度（MDOF）体系输入能量，一般2到3个振形即可。通过非弹性时程分析计算每一个ESDOF体系相对输入能E'1（MDOF）.n，转换成MDOFnth模态输入能贡献为

式中，Γn为模态参与系数。MDOF体系总的输入能为

式（5）的右边被解释为模态能量分解方法。

结构的滞回能需求是基于能量设计方法研究的主要问题之一。通过指定地震加速度下的非线性时程分析，可精确计算结构滞回能需求。由于计算技术的发展，计算多自由度体系在指定地震下的滞回能需求已不是困难，但复杂、费时，不适合与一般的基于能量需求的设计方法相结合。使用反应谱和结构等效SDOF模型在基于力、基于位移的设计方法中已得到解决。Ghosh&Collins[5]探讨了将反应谱用于计算滞回能的可行性，基于非弹性SDOF需求建立了滞回能反应谱，由实际MDOF体系的pushover分析建立对应的等效单自由度体系ESDOF；利用相似关系，将滞回能反应谱值转换成等效ESDOF的滞回能值。但计算结果表明对于某些工况，MDOF体系的实际滞回能需求与用ESDOF计算的需求有相当大的误差，这些差异为后续研究提供了动机。传统pushover分析存在的问题推动了pushover分析技术的研究进展，如“模态”或“自适应”pushover分析。这些新方法用多个ESDOF体系代替单个ESDOF体系分析结构的反应，计算精度得到提高。Prasanth,et al.[6]在文献[5、7、8]研究的基础上提出了考虑高阶振型影响，用多个等效单自由度体系计算MDOF滞回能需求的方法，与MDOF时程分析得出的滞回能需求相比较，有较高的精度。方法如下：

对应第个模态的等效ESDOF动力方程为

式中，振型参与系数Γn=Ln/Mn；Mn=φnTmφn；Ln=φnTmι；2ζnωn=Cn/Mn；Cn=φnTcφn；ωn2=Kn/Mn；Kn=KponφnTfn；Gn（qn）为第n个模态ESDOF体系力、位移关系函数，可从MDOF的非线性pushover分析得到此函数；φn为结构第n个标准化振形，屋顶振幅φrn＝1；ι为单位向量；fn是pushover分析中基于第n个振形、对mφn标准化（fn=mφn/ ιTmφn），使其底部剪力为1的侧向力分布。对每一模态，pushover推覆结构到层间侧移2.5%。

根据曲线所围面积相等的原则将底部剪力Vn与屋顶侧移Dn的pushover曲线用双折线近似（见图1），从双折线得出第n个模态ESDOF的弹性刚度Kpon、屈服位移Dyn=Vyn/Kpon、强化刚度比αkn。

求解非线性动力方程（6），得出每个模态的滞回能需求Enh，对每一条地震波，相加前若干阶Enh值，得到结构的滞回能需求EMPA。

孙国华、顾强等[9]在前人研究的基础上提出了由能量反应谱计算多自由度结构地震滞回能需求的方法。为消除体系质量影响，采用等效速度VEh表述滞回能：

输入地震波，将峰值加速度统一调整至罕遇地震水准0.4g，阻尼比ζ=0.05、后期刚度p=0.05。通过改变SDOF体系的周期T及目标延性μ，得到用单位质量等效速度表述的等延性滞回能谱，图2为6条近场地震波的平均值。

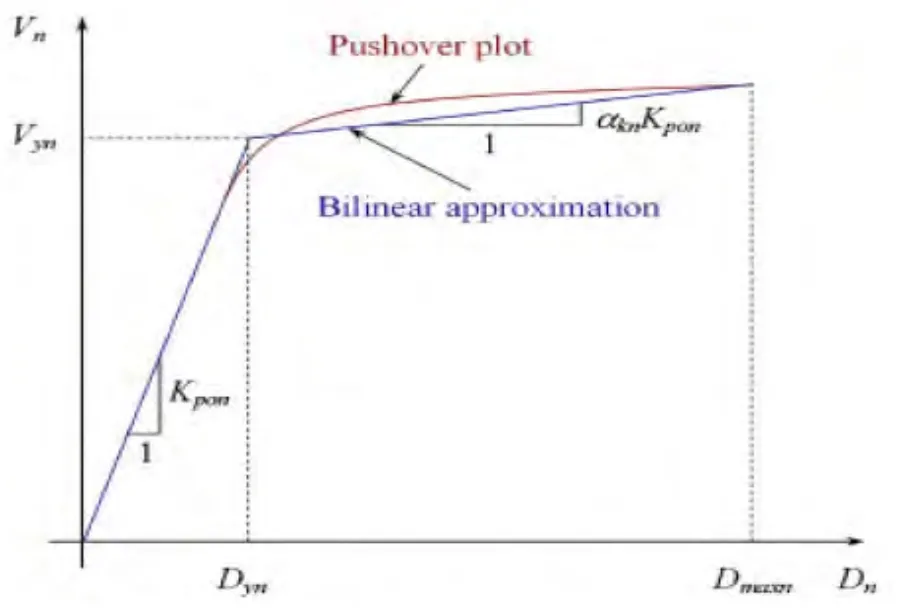
图1 Pushover（Vn-Dn）曲线用双折线性近似[6]

图2 近场罕遇地震滞回能等效速度谱

水平地震下弹塑性多自由度体系（MDOFS）的运动方程为

式中，M为质量矩阵；C为阻尼矩阵；F（u）为恢复力矩阵；u为相对位移，ug为地面位移。如结构反应为第j振型、且振型保持不变，结构楼层位移向量u可用结构顶层广义位移xti近似表示为

式中，Φj为标准化第j振型，即结构顶层幅值φjn=1。将式（9）带入式（8），经简化并积分，得到等效单自由度体系（ESDOFS）的相对能量方程：

（1）对结构进行模态分析，得到周期Tj、标准化振型向量Φj、振型参与系数Гj、等效质量等参数；

（2）对结构进行pushover分析，获得结构的屈服位移Δy、罕遇地震的目标位移Δmax及位移延性系数μ；

（3）根据第（2）步所确定的结构位移延性系数在等延性滞回能等效速度谱上查出前若干阶周期所对应的等效速度VEh，j，按公式（12）计算ESDOFS的滞回能；

式中，EH为多自由度结构体系的累积滞回能需求；n为考虑的振型阶数；为结构第j振型ESDOFS的滞回能；为第j振型等效单自由度体系的广义质量；Гj为第j振型参与系数；mi为第i楼层质量；φij为第j振型在第i层的振幅；Xmass，j为第j振型的振型质量参与系数；N为结构层数。

图3和图4为3个钢框架算例，取前3阶振型，按上述方法计算的近场地震滞回能与真实值（多自由度结构时程分析结果）的对比及结构前三阶振型滞回能的分担比例，图中横坐标为6条地震波编号及平均值。

由图3可知基于能量反应谱确定MDOFS滞回耗能简化方法的结果同真实值吻合良好。近场地震下6条地震波平均结果的误差在-4.84%～-0.75%。

图3 滞回耗能

图4 各阶振型的滞回能分担比例

2 近断层地震动有效滞回耗能

震源机制、断层破裂方向与场地的关系和断裂面相对滑动方向等因素使近断层地震动与远场地震动相比有明显不同的特征，近断层地面运动可分为三种类型：（1）带有向前破裂方向性效应脉冲（forwad directivity pulses），见图5；（2）带有滑冲效应脉冲（fling-step pulses）；（3）不带有速度脉冲。第（3）种类型的近断层地面运动与远场地面运动的特征相似。

研究表明，断层破裂从某区域开始逐渐向外扩展，当断层以接近地壳介质剪切波速的速度破裂时（断层破裂速度一般稍小于剪切波速），地震波的能量在很短的时间内几乎同时到达破裂前方的某一点。由于能量的累积效应，在速度时程的开始阶段形成一个持时相对较短、峰值较大的速度脉冲（见图6a）。这种能量累积并未改变通过各点的总能量，只是改变了通过各点的总能量在时间上的分布，即能量密度，它使破裂传播方向上场点的能量密度增大。

滑冲效应产生的原因是断层两盘的相对运动使地震动速度时程中出现单方向半脉冲（见图7a），地面出现阶跃式的不可恢复位移，这种位移被称为“fling step”。滑冲效应可能出现在走滑（strike-slip）断层地震中平行断层走向的方向或倾滑（dip-slip）断层地震中的断层滑动方向。

图5 方向性效应示意[10]

图6 有forward directivity脉冲的近场地震波速度、位移时程

图7 有fling-step脉冲的近场地震波速度、位移时程

由图6、图7可见近断层地面运动的两个重要特征是强速度脉冲和永久性地面位移，地震波的单个强速度脉冲或系列长周期的高振幅速度脉冲导致在很短时间内对结构输入了较大的能量，使结构产生严重破坏。而远场地震波不存在明显的速度脉冲，对结构的能量输入是一个逐渐累积的过程，结构往往由于累积能量导致累积损伤破坏。脉冲型地震动对工程结构有着特殊影响，时程中脉冲的个数与结构的反应直接相关，当脉冲周期与结构自振周期相近时，共振使得结构的反应明显大于普通地震动，使结构失效的可能性大大增加。

为研究强脉冲对结构破坏的潜在影响，Kalkan[11]分析了前破裂方向性、滑冲效应速度脉冲地面运动特征与结构需求的关系，根据近断层地震记录的能量特征，提出了新的结构能量需求指标－有效循环能量ECE（有效持时内输送给结构的能量）作为量化近断层地震破坏能量的表述。经过对大量结构的确认性研究，提出了不需进行非线性时程分析，判断多自由度（MDOF）体系能量需求的ECE谱。

为研究近场地震影响，孙国华、顾强[12]根据多条硬土场地的近场地震记录，建立了最大有效滞回耗能MECE（Maximum Effect Cyclic Energy）谱。近断层地震记录的强速度脉冲导致结构在瞬间达到最大变形，极易发生损伤和破坏，图8给出了弹塑性单自由度（SDOF）体系（周期T=2 s，阻尼比ζ=0.05，后期刚度p=0）在近断地震记录Landers/22140 Joshua Tree下的响应。

图8 弹塑性SDOF体系在近场地震下的响应

由图8可见强速度脉冲使得弹塑性SDOF体系在极短时间内达到了最大变形，而随后的地震激励过程中结构变形均比较小，说明近场地震下结构在瞬时强速度脉冲内达到最大响应，结构破坏主要由速度脉冲所携带的瞬间地震输入能量所致。为了寻求近场地震下更为合理的能量设计依据，文献[12]选用总滞回耗能的部分能量，即SDOF体系在达到目标延性时第一象限或第三象限中骨架曲线所包络的单向推覆能量为新的能量指标，将其定义为最大有效滞回耗能MECE，即图9中影线面积OABCO。由图9可见，在近场地震激励下计算弹塑性SDOF体系最大有效滞回耗能的关键是求解系统达到目标延性μt时对应的Vy和uy，一般需要迭代计算。数值分析中发现：无论是正向还是反向，终究有一个方向会达到最大目标延性，此时所对应的系统屈服剪力Vy、屈服位移uy才是真解。随着系统Vy、uy、μt的确定，最大有效滞回耗能（影线面积OABCO）成为了稳定的指标。近场地震激励下，超越系统屈服塑性滞回非常少，仅出现在大的速度脉冲内，采用最大有效滞回耗能MECE作为设计指标更为合理。

由图9的几何关系，有双线性恢复力特性的弹塑性SDOF体系最大有效滞回耗能可按公式（15）计算。

最大有效滞回耗能的等效速度为

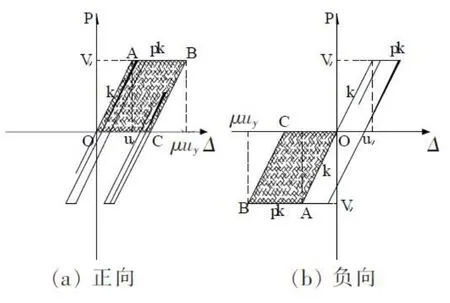
图9 最大有效滞回耗能示意图

图10 最大有效滞回耗能等效速度谱（罕遇地震水准）

式中，Vy为系统屈服剪力；uy为系统屈服位移；p为系统的后期刚度系数；μt为系统的目标延性；m为系统质量。建立的MECE等效速度Veq谱如图10所示。

3 基于能量平衡的设计方法

一旦根据地面运动建立了能量需求，结构应该提供充分的能量耗散能力。Chao&Goel[13]认为得到结构在设防地震下可预期、可控制的性态取决于3个因素：（1）结构经受强震时，沿高度的设计侧向力分布应能代表结构实际的层剪力分布，大多数设计规范的倒三角形分布模式源于弹性分析，对非弹性状态不一定正确；对于性态设计，应采用源于结构非线性动力分析，并经校核的设计侧向力分布模式；（2）结构损坏被限定在预设的部位是较理想的；由于结构强震时的弹塑性性能，弹性设计方法不能保证结构形成可预期的机构，基于性态设计根据预期的结构屈服模式，采用塑性设计方法是较合理的；（3）可用预定的侧移指标确定结构设计底部剪力；层间侧移是合适的控制参数，可作为对应指定震害水准的结构性态（如正常使用，防止倒塌）指标。

为了计算结构设计基底剪力，得到强震区结构的能力需求如强度、延性、能量耗散，研究人员提出了不同的方法，能量平衡方法是其中之一。能量平衡方法假定单向推覆结构到目标侧移需求的能量等于按弹性反应谱的拟速度计算的最大地震输入能。用此方法计算结构的地震能量需求，不需时程分析，但仅适用于结构初步设计。Leelataviwat，et al[14]将能量平衡方法用于预期的屈服机构，提出了基于性态的塑性设计方法，用对应设防地震拟速度谱的输入能量得出结构对应预期屈服机构目标最大侧移所需的基底剪力。方法局限于中等高度的结构,用于高层和低层结构误差很大。

Chao&Goel[13]强调在反应谱的等加速度区间可以用设计拟速度计算地震输入能量，采用能量平衡方法计算折减后的结构设计底部剪力；但在反应谱的等位移区间和等速度区间，结构最大的非弹性位移和弹性位移相等或接近相等，结构位于这些区域时不考虑结构的周期和延性能力与地震力延性折减系数的关联，直接用设计拟速度计算输入能量，采用能量平衡方法不能得出可靠的结构设计底部剪力；需要根据地震力延性折减系数的概念，在基于能量的抗震设计方法中提出合理的改进措施计算结构设计底部剪力。基于文献[13]的观点，Chao&Goel和Lee[13，15-17]分别对偏心支撑钢框架、抗弯钢框架、中心支撑钢框架和特殊桁架式抗弯钢框架基于能量的性态设计方法进行了研究，将能量平衡和能力方法用于结构设计，通过建立结构的预期屈服机构、目标侧移、结构的力－位移特性与设防地面运动的弹性输入能之间的简单联系计算所需的设计底部剪力。设计过程起始于为结构选择一个预期的屈服机构，抗弯钢框架屈服机构的塑性铰只限于梁端和柱脚，偏心支撑钢框架屈服机构的塑性部位只限于耗能梁段和柱脚（见图12），中心支撑钢框架屈服机构的塑性部位只限于受压撑杆屈曲和柱脚形成塑性铰；特殊桁架式抗弯钢框架屈服机构的塑性部位只限于每层桁架梁跨中无斜腹杆节间上下弦杆端部形成4个塑性铰及柱脚塑性铰。指定设防水准地震下预期屈服机构的侧移限值，基于结构反应修正系数和位移放大系数的概念，对按拟速度计算的弹性地震输入能进行修正。利用设防地震下将结构推覆至屈服机构状态，并达到指定目标侧移的修正地震输入能量与屈服机构侧向力做功的能量平衡得出对应结构预期性态的设计底部剪力。使用层剪力分布系数（根据结构非线性动力分析得出的层剪力沿结构高度的分布规律）描述基于结构非线性反应的侧向力分布模式，然后按能力方法设计构件。偏心支撑钢框架（EBF）[13]的设计方法、步骤如下：

（1）由非线性时程分析得出EBF的层剪力分布系数，用于确定设计侧向力分布。

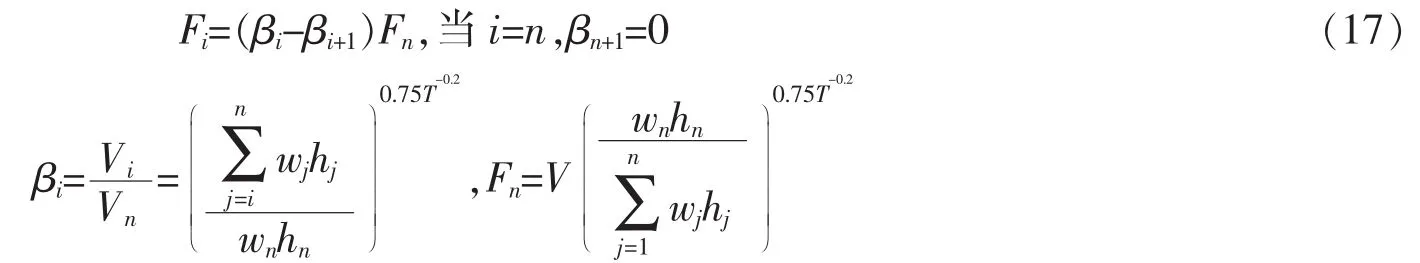
式中，βi为第i层的剪力分布系数；V为设计底部剪力；Vi和Vn分别是第i层和顶层（第n层）剪力；wi和wj分别是第i、j层的重力；hi和hj分别是第i层、第j层距地面的高度；wn是结构顶层的重力；hn是屋顶距地面高度；T是按规范公式计算的结构基本周期；Fi和Fn分别是作用在第i层和顶层（第n层）的侧向力。式（17）的侧向力分布模式可以使屈服沿高度分布比较均匀，避免屈服集中在少数楼层。

（2）利用将结构单调推覆形成所预定的屈服机构，并达到目标侧移时的能量平衡关系得到设计底部剪力。假定侧向力作功等于修正系数γ乘以设防地震单质点体系弹性输入能，E与地震时结构能量耗散并未发生联系，系数γ与对地震输入能有较大影响的结构自振周期有关。能量关系为

Ee和Ep分别是将结构推覆到目标侧移所需能量的弹性和塑性部分；Sv是弹性设计拟速度；M是系统总质量。系数γ取决于结构延性系数μs和与结构周期有关的延性折减系数Rμ=Ceu/Cy，由图11单质点弹性体系和弹塑性体系底部剪力与侧移的几何关系得到

式中，μs=△max/△y，结构延性系数；Rμ为延性折减系数，可根据μs得出。

图11 结构反应及能量平衡[13]

图12 预选的偏心支撑钢框架屈服机构[13]

由规范的弹性设计拟加速度谱得到弹性能量需求E。设计拟加速度可表示为

式中，A为设计拟加速度；g为重力加速度；Ce为标准化的设计拟加速度，能量关系可表示为单自由度体系弹性能Ee按下式计算：

式中，V为屈服底部剪力；W＝Mg，结构总重力。

由式（21）、（22）得出

根据预选的屈服机构（见图12），令塑性能Ep等于设计侧向力（式17）所做的外力功，得

式中，θp为结构的整体非弹性倾角，即预定的目标侧移角θu和屈服侧移角θy的差值。

由式（17）、（23）、（24）得出

式中，V为设计底部剪力；α为无量纲参数，与结构刚度、屈服模式和预期的目标侧移有关。

公式（25）给出的设计底部剪力对应屈服平台段（图11中CyW）,而现行规范基于强度设计方法给出的底部剪力对应于第1个显著屈服点，可视为图11中CsW。

（3）耗能梁段内力

研究表明剪切耗能梁段受力沿结构高度的分布与用剪力分布系数βi表示的层剪力分布接近。已知图12中EBF耗能梁段的塑性转角为，由内外功相等得

式中，L为跨度；e为耗能梁段长度；Vpr为最顶部耗能梁段受力；第i层耗能梁段所受塑性剪力为βiVpr；Mpc为底层柱所需的塑性弯矩；wiu为梁上竖向荷载。

文献[13]建议：

V'为单跨的底部剪力，等于V除以有支撑跨的数量；h1为底层高度。

根据式（27）、（28），得出第i层耗能梁段所受塑性剪力为

求出各层耗能梁段所受塑性剪力后，可由平衡关系、根据能力设计方法得出各构件截面。

Kim&Choi[18]将能量平衡方法用于带屈曲约束支撑（BRB）钢框架的抗震设计，利用弹性设计反应谱得出的地震输入能计算结构的能量需求,由能量需求与BRB耗散的能量相等得出支撑截面。通过三种场地的60条地震记录的时程分析，研究了用等效单自由度体系计算带有屈曲约束支撑的多层结构地震输入能和滞回能需求的有效性，将得出的层滞回能需求模式用于所提出的设计方法。具体步骤如下：

单自由度体系单位质量地震输入能Ei为

式中，M为质量；Sv、Sa分别为拟速度、拟加速度；ωn表示圆频率。根据能量平衡关系，将（30）式的输入能视为等效弹性体贮存的能量，由原弹塑性体系的弹性能Ee和塑性能Ep构成（见图13），Ee和Ep由下式表示

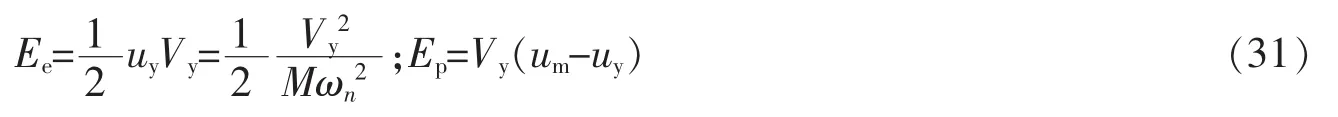
uy和um分别为结构屈服位移、最大位移。将最大位移用目标位移uT替换，公式（30）可写成

由式（30）、（32），得出体系经受指定的地震动，变形达到目标位移时的底部屈服剪力。从输入能减去弹性能，BRB耗散的单位质量塑性能为

假定BRB为理想弹塑性，设置如图14所示，BRB变形到最大位移耗散的塑性能Epb用式（34）表示。

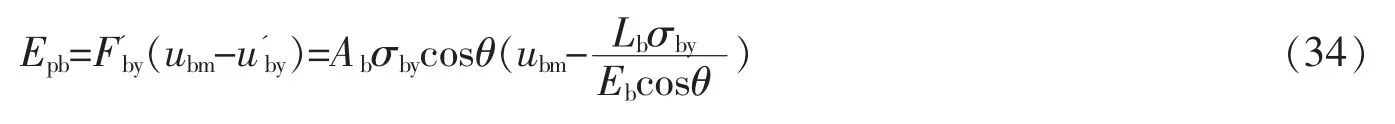
图13 结构的力－位移关系和等效弹性体系[18]

图14 屈曲约束支撑框架的变形[18]

框架梁柱铰接，按抵抗重力荷载及支撑引起的荷载设计，在设防地震下保持弹性。假定能量全部由BRB耗散。支撑设计方法如下：

（1）确定屈服位移和目标位移

如果每一层的层高及支撑屈服应力相等，结构的屈服位移等于层屈服位移乘以层数N。

体系的屈服位移式（35）与支撑的截面积无关，可在得出支撑截面之前先确定屈服位移、目标位移uT。

（2）转换成等效SDOF体系

应用能量平衡关系前，需将原多层结构的屈服位移、目标位移转换成等效SDOF的对应值。

式中，φt1是基本振形向量对应顶层的幅值，Γ1是振形参与系数。初步设计阶段，可假定基本振形为线性。基本振形的有效参与质量为

（3）确定结构基本周期及输入能Ei

由结构基本周期T，从弹性设计反应谱得出拟加速度Sa，由式（30）得到地震输入能。初步设计阶段需假定基本周期，得出BRB截面后可用特征值分析得出周期修正值。

（4）由式（32）计算底部屈服剪力Vy，代入（33）式得出BRB耗散能

（5）塑性能的层分布模式

为使每个支撑得到充分利用，使BRB的塑性变形不集中在少数几层，将得出的塑性能Ep沿高度适当分布，一般情况可采用简单的线性层间分布模式，文献[18]采用模型结构20条地震波时程分析结果作为塑性能需求的层间分布模式。

（6）确定BRB截面积Abi

根据步骤（5）得出的塑性能与BRB变形到目标位移uT的塑性能相等得出每一层BRB的截面积

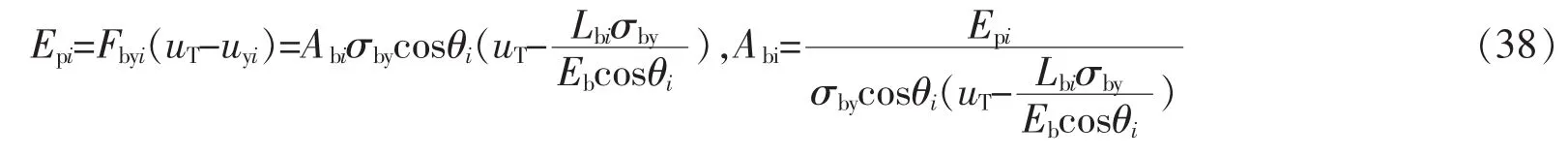
式中，Epi为第i层分布的塑性能；Fbyi为层间屈服力；Abi、Lbi、θi分别为第i层BRB截面积、长度、转角。

（7）设计优化

根据假定的基本周期和振形，得出塑性能量和BRB截面的初始值，由特征值分析可得出结构基本周期和振型的较精确值。用修正的基本周期和振形，得出BRB截面，重复此过程直到收敛。

文献[13-18]所提出的能量设计方法均未考虑累积地震输入能与结构单向推覆耗能之间的不对应关系。结构非弹性时程分析得出的滞回能包含了多次荷载反向，为结构的累积滞回能。文献[13-18]基于能量设计方法的依据是设计输入能量等于结构内部耗能或侧向外力功，问题在于预选屈服机构的侧向力做功或结构内部耗能为单调加载的推覆耗能，和地震的累积滞回能量是不对应的，需要研究地震动输入的累积滞回能与结构单调荷载推覆耗能之间的关系。

4 基于滞回耗能的设计方法

用拟速度计算的输入能量公式（30）对于弹性单自由度体系是正确的，用其预估多自由度弹塑性体系的能量需求，只是权宜之计。文献[13、15－18]所给出的能量需求与单调推覆结构耗散的能量没有明确的对应关系，其合理性值得商榷。在实际结构的周期范围，结构延性增加，输入能量趋向于减少，用拟速度表述的地震输入能无法考虑这一现象，有时也会低估能量需求。文献[13]简单假定即使结构某些部位的应力超过了弹性极限，其能量输入公式近似正确，但也明确表示其输入能量计算方法有待根据新的研究成果进行改进。文献[18]中的单自由度转换方法也不能改善依据弹性输入能量公式计算滞回能需求的不合理性。

Akbas，et al.[19]研究了钢框架在不同地震动下的能量需求，给出了结构基本周期与总输入能、滞回能、阻尼能的图解关系；根据已有的试验数据，研究了强震下经受较大非弹性变形的楼层梁滞回能力；提出了规则抗弯钢框架对应防止倒塌水准的性态设计方法。能量需求由滞回能及沿框架高度的分布给出，框架的抗力取决于楼层梁的能量耗散能力，滞回能仅由梁端塑性铰耗散，柱子保持弹性。方法如下：

（1）根据重力荷载组合初选框架截面。

（2）在临近倒塌状态，将设计滞回能Edh表示成

式中，Eh为滞回能输入；γ为设计能量输入系数；S为场地系数，文中建议软土场地S=1.5，硬土场地S=1.0，基岩S=0.5，可线性插值得出其它场地系数S值；E1为总输入能量，可根据设计地面运动强度、框架层数，由图15的能量相关曲线得到；ED为阻尼能，由经验公式得出。

式中，α为阻尼能ED与总输入能EI之比，文中给出了系数α的建议值。

（3）假定Edh沿结构高度的层分布为线性关系，表示为

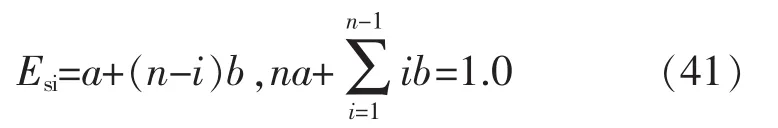
式中，Esi为第i层耗散的累积滞回能；n为层数；a、b为系数，对中、高层结构a=0，对低层结构a=b。根据每层各梁端耗散能量相等，得出每根梁的滞回能需求Eed。每层耗散的滞回能Esi等于同层各梁耗散能量之和。

式中，j为同层梁的数量。

图15 相关曲线[19]

（4）文献[19]根据有限的试验数据，提出翼缘焊接、腹板栓接的梁柱抗弯连接（WFBW）的累积塑性转动能力θpa在0.05～0.5之间，假定平均的θpa在0.05～0.1之间。钢梁的耗能能力Eec为

式中，Mp为梁截面塑性弯矩。

（5）根据梁的滞回能需求，确定柱子的弯矩和轴力，倒塌状态各梁端弯矩Mi为

式中，Eed为单根梁的滞回能需求，θpa为累积塑性转动能力。根据节点平衡关系得出各柱段的弯矩、轴力。文中指出如此计算柱内力有两个缺点：在梁端实际上并没有进入屈服的情况下会低估柱子内力；可能不满足层间位移限值。

（6）强柱弱梁验算

文献[19]的特点是建立了能量需求与结构累积耗能能力之间的对应关系，局限性在于图15的输入能曲线仅能用于多层钢框架，不能用于其它结构体系，不具有一般性。

结构在远场地震作用下的损伤与地面加速度的循环特征密切相关，累积滞回耗能成为表征此类地震破坏的合理指标。Choi[20]将滞回能谱、累积延性谱用于屈曲约束支撑钢框架基于性态的抗震设计,由20条地震记录建立了滞回能谱和累积延性谱。滞回能谱（见图16）的横座标为单质点体系的周期，纵座标为滞回能与质量之比。累积延性谱（见图17）的横座标为单质点体系的周期，纵座标为往复振动位移绝对值之和与屈服位移的比值。

图16 等延性滞回能谱[20]

图17 各种目标延性比的累积延性谱[20]

结构耗散的滞回能取决于塑性变形，使用滞回能谱设计结构需要先清楚结构累积塑性变形量，这可以由累积延性谱（弹塑性单自由度体系由地震激励引起的累积延性比与周期和目标延性的关系）得到。累积延性为正、负屈服侧移之和，如图18所示。文献[20]的方法及步骤如下：

图18 累积塑性变形[20]

（1）根据屈曲约束支撑（BRB）屈服应力、长度计算屈服位移（参见图14）。由给定的目标位移uT得出目标延性比。

式中，θ、Lb、Eb、σby分别为BRB的转角、长度、弹性模量、屈服应力。

（2）按美国IBC-2000，假定支撑框架基本周期

（3）初定BRB截面

竖向承载体系（框架）设计成弹性，梁柱铰接，全部输入能由屈曲约束支撑耗散。由支撑的累积塑性能量耗散等于滞回能需求得出满足目标延性的支撑截面积。

式中，Eh、Fyj、juyj、μa分别为由滞回能谱得出的滞回能，第j层的屈服力、屈服位移，由累积延性谱得到的累积延性比；Abj、Lbj、θj、σby、Eb分别为第j层BRB截面积，长度，转角，屈服应力，弹性模量；N为结构层数。第j层BRB截面积可由底层BRB截面积Ab1乘以层滞回能分布比DRj得出，层滞回能分布比DRj可从结构经受地震记录的时程分析或简化的三角形分布得到。

由式（47）、（48）得出

（4）终定BRB截面

基于式（46）假定的周期初定BRB的截面后，可对结构进行特征值分析，得出修正的周期，重复此过程，直到周期收敛。

Choi[20]给出了3层、8层带有屈曲约束支撑钢框架设计实例，20条地震波的时程分析显示顶层位移的平均值与指定的性态目标位移吻合较好，沿结构高度层间侧移分布均匀。Choi[20]的方法较文献[13-18]的能量平衡方法前进了一步，因滞回能直接来源于时程分析建立的累积滞回能谱，支撑耗散的能量也是累积滞回能，用累积延性谱在累积滞回能与结构单调推覆能量耗散之间架起了桥梁，概念清晰、操作简单，但提出的滞回耗能谱、累积延性谱仅根据选定的少量地震波得出，地震波数量偏少；因累积延性比定义为累积塑性变形（不含有弹性变形）与屈服位移的比值，公式（47）、（49）中的（μa-1）应为μa。

孙国华、顾强[21]在Choi[20]研究的基础上，引入累积延性比，建立了标准化的滞回耗能谱、累积延性比谱，引入捏缩系数反映梁、柱、剪切墙板的滞回特性，提出了钢板剪力墙结构（SPSW）基于能量的性态设计方法如下：

（1）标准化滞回耗能谱

将弹塑性单自由度（SDOF）体系塑性滞回耗能Eh用等效速度VEh表示为

式中，βEh为单自由度体系滞回耗能的等效速度与地震最大峰值速度的比值。文献[21]根据420条地震记录，建立了四种场地的标准化滞回耗能谱（见图19）及各参数的表达式。图19中T为结构自振周期；T1为谱曲线水平段开始点对应的周期；T2为谱曲线下降段开始点的周期；γ为曲线形状参数；η1为与阻尼比相关的系数；REh，μ为延性折减系数；βEh，max为单自由度体系滞回耗能的等效速度与地震波峰值速度比的最大值。

图19 标准化等效滞回耗能谱[21]

目前，大多数规范仍以地面峰值加速度PGA作为地震动强度指标，公式（50）是以地面峰值速度PGV作为不同地震水准的地震动强度指标。考虑到地震波峰值加速度PGA与PGV指标的离散性，文献[21]采用对同批大样本地震波的幅值按两种地震动强度指标PGA和PGV分别进行调整，输入给同一弹塑性SDOF体系，以两种地震动指标调整的同批地震波输入下SDOF体系的能量反应相等为原则，提出了与我国偶遇、罕遇地震水准相一致的，按PGVdesign地震动强度指标表征的地震动水准。420条地震波的统计公式为

（2）累积延性比谱

地震激励下，结构经历了无规律的往复滞回耗能，致使结构出现累积损伤。用累积延性比NEh，μ衡量结构累积损伤程度，累积延性比NEh，μ为

式中，Eh，μ为结构在地震作用下的累积滞回耗能；Fy为结构的屈服承载力；σy为结构的屈服侧移。累积延性比NEh，μ也可视为结构经历的所有塑性变形与结构屈服位移之比，反映了结构在地震激励下累积变形的程度。通过设定SDOF体系的恢复力模型、给定体系的目标延性系数μ，并不断改变体系的周期T，便可获得目标延性下的NEh，μ谱。文献[21]基于大样本地震波的弹塑性时程分析，并考虑结构周期T、阻尼比ζ、延性系数μ以及后期刚度p等影响因素，建立了累积延性比谱的实用计算式（53），分析表明周期的影响不敏感，可以忽略。

其中，f（ζ）=0.92ζ+0.95；f（p）=（-5.5μ+5.5）p2+（1.35μ-0.3）p+1；f（μ）=0.8μ2+1.1μ-1.9。

（3）基于滞回耗能谱的钢板剪力墙结构性态设计方法

设定SPSW结构在罕遇地震下形成剪力墙板屈服，梁两端、底层框架柱根部出现塑性铰的理想塑性机构。初选构件截面后，可由特征值分析得到结构的各阶周期。设定结构的整体目标延性μ，采用叠加原理，按文中公式（12）～（14），由标准化的滞回耗能谱得出结构总滞回耗能，式中VEh，j应为按图19及式（50）计算的第j振型等效速度。

（3.1）累积延性比

SPSW结构的楼层屈服位移按式（54）计算。

式中，Ry，i为第i层墙板的材料超强系数；σy，i为第i层墙板的屈服强度；hi为第i层层高；E为材料弹性模量；αi为第i层墙板拉力场方向与竖向的夹角，初步设计时可假定为45°。

初步设计时可先指定结构的第i层层间极限侧移δu，i。迭代设计过程中，可通过对初选截面的SPSW结构进行推覆分析，计算结构最大层间侧移比达到限值时每层的实际层间侧移δu，i。由式（55）确定μu，i，由式（53）得到各层的累积延性比NEh，μ。

（3.2）设计基底剪力

根据设定的罕遇地震下性态，SPSW的累积滞回耗能由三部分构成：①钢板剪力墙耗能（Eh，w）；②框架梁两端耗能（Eh，b）；③底层框架柱根部耗能（Eh，c）；由式（56）～（59）确定。

①剪力墙板累积滞回耗能

式中，ηw为剪力墙板滞回环的捏缩系数；ζep为等效粘滞阻尼比；Vy，w，i为第i层剪力墙板的屈服剪力；uy，i为第i楼层屈服位移；pw，i为第i层剪力墙板的后期刚度系数；μui为第i层的目标延性；NEhμ，i为第i层的累积延性比。

②钢梁两端塑性铰累积滞回耗能

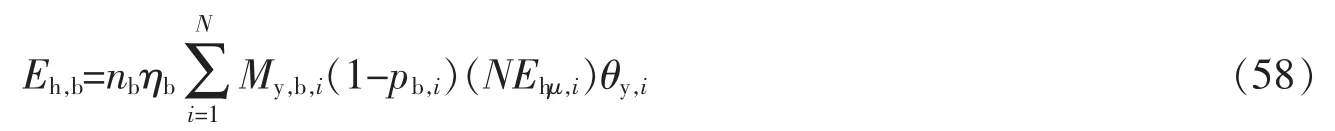
式中，nb为同层梁中塑性铰的数量；ηb为钢梁滞回环捏缩系数；My，b，i为第i层钢梁的塑性弯矩；pb，i为第i层钢梁的后期刚度系数；θy，i为第i层钢板剪力墙结构屈服时的层间转角。

③钢柱根部塑性铰累积滞回耗能

式中，nc为柱底塑性铰的数量；ηc为钢柱滞回环捏缩系数；My，c，1为底层钢柱塑性弯矩；Nc，1为底层柱中轴力；Ny，c，1为底层钢柱截面屈服轴力；pc，1为底层钢柱的后期刚度系数。

采用文献[13]的层剪力分布系数式（17），由式（60）得出SPSW结构钢板墙分担的底部设计剪力

（3.3）楼层剪力由下式计算

（3.4）罕遇地震下SPSW结构的剪力墙板厚度可根据式（62）[22]确定

式中，tw，i为第i层剪力墙板的厚度；σy为钢材屈服强度；Lcf为剪力墙板的净宽度；αi为第i层墙板拉力场的倾角（与竖向的夹角），可取α=45°。梁柱截面初步确定后，也可按式（63）[22]计算α角。

式中，Ac，i为第i层钢柱截面积；Ab，i为第i层钢梁截面积；Ic，i为第i层钢柱截面绕垂直墙板轴的惯性矩；L为带墙榀SPSW结构的柱轴线跨度；hi为第i层层高。

（3.5）按能力设计方法确定周边构件截面。初步设计时可根据初选构件截面计算结构周期、模态，确定SPSW结构内填钢板墙的厚度。随后，可通过对优化截面的SPSW结构的模态分析，对墙板及周边构件进行迭代设计，重复此过程至设计收敛。

文献[21]的远场地震下标准化滞回耗能谱－累积延性比谱设计方法建立了滞回耗能需求与结构单向推覆耗能能力之间的明确关系，但文献[21]中标准化滞回耗能谱的场地类别划分与我国规范不一致，结构延性μ的计算方法也需进一步完善。

5 基于有效滞回耗能的设计方法

结构破坏与地面运动特征密切相关，但大多数研究[1-6，13-19]并没有明确地区分远场地震加速度的循环特征和近场地震速度的脉冲特征。孙国华、顾强[12]根据多条硬土场地的近场地震记录，建立了最大有效滞回耗能谱（Maximum Effect Cyclic Energy，MECE），提出了近场地震下基于MECE谱确定钢板剪力墙结构屈服基底剪力的性态设计方法，如下：

根据结构周期及整体位移延性系数μt直接从最大有效滞回耗能等效速度谱查出前N阶的等效速度，即Vh，1、Vh，2，…，Vh，N，采用叠加原理考虑弹塑性阶段结构高阶振型的影响。由公式（64）计算多自由度结构的有效滞回耗能。式中参数定义同公式（12）～（14）。

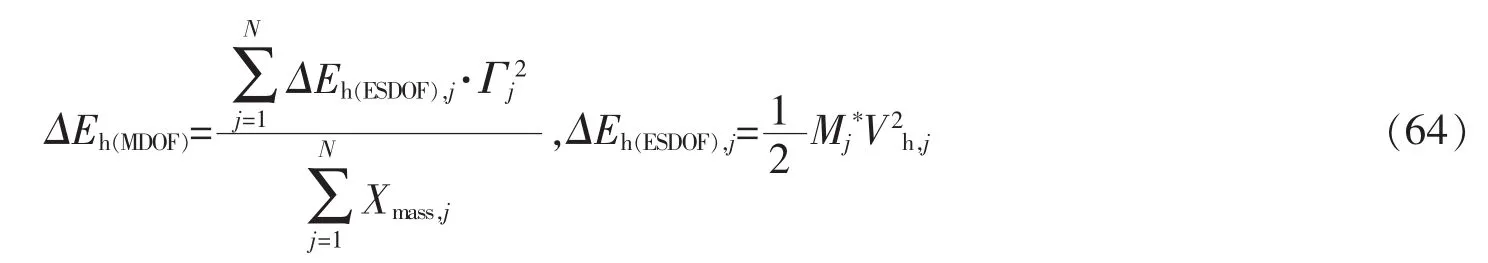
式中，△Eh（MDOF）为多自由度体系的有效滞回耗能需求；△Eh（ESDOF），j为结构第j振型的等效单自由度有效滞回耗能需求。为获得合理的有效滞回耗能，应取振型质量参与系数之和大于90%以上，一般情况下，取前三阶振型即可满足要求。结构的设计过程与文献[21]相类似，但各构件耗能计算式中不再出现公式（57）-（60）中含有累积延性比的括号项。

文献[12]的近场地震MECE谱设计方法建立了近场地震有效滞回耗能需求与结构单向推覆耗能能力之间的明确关系，但文献[12]中近场地震的MECE等效速度Veq谱仅根据10条硬土场地的近场地震记录提出，地震波数量少，尚应补充一定数量的各种场地带速度脉冲的近场地震记录，特别是国内的近场地震记录，建立各种场地的MECE等效速度Veq谱。

6 结语

我国是地震多发区，国内外的数次强烈地震给我们留下了惨痛的教训。越来越多的结构研究、设计人员赞成未来的抗震设计需要基于多种性态目标，部分国家的建筑工程抗震设计规范也正在发生根本性的变化。结构基于能量抗震设计方法的研究在国内外正处于起步阶段，由于问题的复杂性、多面性，前人所提出的设计方法各异，研究成果距离工程应用尚有距离。

提出基于性态的结构抗震设计理论及实用方法，为基于结构性态抗震设计规范的制定提供技术储备，对已建大型复杂结构进行强震下的性态评估，有重要的理论意义和实际需求。基于性态抗震设计方法能被用于实际工程之前还将面临若干挑战，任重而道远，需要各国学者联合起来不懈努力去完成。

[1]Chung-Che Chou,Chia-Ming Uang．An evaluation of seismic energy demand：An attenuation approach[R]．Berkeley：PEER Report 2000/04 Pacific Earthquake Engineering Research Center,2000．

[2]McKevitt W E,Anderson D L,Cherry S．Hysterretic energy spectra in seismic design[C]//Proceedings of the 2ndWorld Conference on Earthquake Engineering,1980,7：487-494．

[3]Payam Khashaee．Energy-based seismic design and damage assessment for structures[D]．Dallas：Southern Methodist University,2004．

[4]Chou C C,Uang C M．A procedure for evaluation of seismic energy demand of framed structures[J]．Earthquake Engineering and Structural Dynamics,2003（32）：229-244．

[5]Ghosh S,Collins K R．Merging energy-based design criteria and reliability-based methods：exploring a new concept[J]．Earthquake Engineering and Structural Dynamics,2006,35（13）：1677-1698．

[6]Tholen Prasanth,Siddhartha Ghosh,Kevin R Collins．Estimation of hysteretic energy demand using concepts of modal pushover analysis[J]．Earthquake Engng Struct Dyn,2008,37：975-990．

[7]Chopra A K,GoelR K．A modal pushover analysis procedure for estimating seismic demands for buildings[J]．Earthquake Engineering and Structural Dynamics,2002,31（3）：561-582．

[8]Chopra A K,GoelR K．A modal pushover analysis procedure to estimae seismic demands for unsymmetric-plan buildings[J]．Earthquake Engineering and Structural Dynamics,2004,33（8）：903-927．

[9]孙国华，顾强，何若全，方有珍．基于能量反应谱的抗弯钢框架结构能量计算[J]．土木工程学报，2012，45（5）：41-48．

[10]李爽，谢礼立．近场问题的研究现状与发展方向[J]．地震学报，2007，29（1）：102-111．

[11]Erol Kalkan．Prediction of seismic demands in building structures[D]．California：University of California,2006．

[12]孙国华，顾强，何若全，杨文侠．近断层地震作用下钢板剪力墙结构基于MECE谱的性态设计方法[J]．建筑结构学报，2012，33（5）：105-117．

[13]Shih-Ho Chao,Goel S C．Performance-based seismic design of EBF using target drift and yield mechanism as performance criteria[R]．Department of Civil and Environmental Engineering,College of Engineering,The University of Michigan,2005．

[14]Leelataviwat S,Goel S C,Stojadinoviĉ．Toward performance-based seismic design of structures[J]．Earthquake Spectra,1999,15（3）：435-461．

[15]Soon-Sik Lee．Performance-based design of steel moment frames using target drift and yield mechanism[D]．Michigan：The University of Michigan,2002．

[16]Shih-Ho Chao,Goel S C．Performance-based plastic design of seismic resistant special truss moment frames[R]．Department of Civil and Environmental Engineering,College of Engineering,The University of Michigan,2006．

[17]Shih-Ho Chao,Goel S C．A seismic design method for steel concentric braced frames for enhanced performance[C]//4thinternational conference on earthquake engineering,Taipei,Taiwan,2006．

[18]Jinkoo Kim and Hyunhoon Choi．Energy-based seismic design of structures with buckling-restrained braces[J]．Steel and Composite Structures, 2004,4（6）：437-452．

[19]Akbas B,Shen J,Hao H．Energy approach in performance-based seismic design of steel moment resisting frames for basic safety objective[J]．Struct．Design Tall Build．2001（10）：193-217．

[20]Hyunhoon Choi,Jinkoo Kim．Energy-based seismic design of buckling-restrained braced frames using hysteretic energy spectrum[J]．Engineering Structures,2006,28（2）：304-311．

[21]孙国华，顾强，何若全，方有珍．基于滞回耗能谱的钢板剪力墙结构性态设计方法[J]．建筑结构学报，2011，32（11）：126-133．

[22]AISC．Design guide 20-steel plate shear walls[R]．San Francisco：American Institute of Steel Construction,2007．

Energy-based seismic design of steel structure：state of development

GU Qiang,SUN Guohua
（School of Civil Engineering,SUST,Suzhou 215011,China）

Performance-based seismic design has been gaining great attention and development,Chinese seismic design code has accepted performance-based design concept．Because the insufficiency of research works,the current seismic design codes in all countries have not proposed an efficient and general design methodology for the design of structures at multiple performance and hazard levels,further research and development are required．This paper deals with the developmental state and unresolved issues of energy-based seismic design of steel structures．

steel structure;hysteretic energy;performance;seismic design

TU391；TU352.11

A

1672-0679（2015）01-0001-17

（责任编辑：经朝明）

2015-03-01

国家自然科学基金项目（51278320）

顾强（1953-），男，辽宁锦州人，教授，博士，从事钢结构研究，Email：guqiang383@163.com。