一种NLOS量测平滑算法在MAUVs协同定位中的应用

马朋, 张福斌, 田冰, 徐德民

(1.西北工业大学 航海学院, 陕西 西安　710072; 2.中国人民解放军69016部队, 新疆 乌鲁木齐　830001)

一种NLOS量测平滑算法在MAUVs协同定位中的应用

马朋1, 张福斌1, 田冰2, 徐德民1

(1.西北工业大学 航海学院, 陕西 西安710072; 2.中国人民解放军69016部队, 新疆 乌鲁木齐830001)

摘要：在基于双领航者的MAUVs协同定位过程中，为了减轻NLOS量测误差的影响，在假设NLOS修正偏差先验已知的前提下，以4状态Markov链描述了4种LOS/NLOS量测模型间相互独立转换过程，继而利用交互多模和Kalman滤波理论设计了一种AUVs间相对距离量测平滑算法，并将其距离量测估计结果应用于MAUVs协同定位系统中。仿真结果对比表明，该算法可以有效提高AUVs间的相对距离量测估计精度，获得了更好的协同定位性能。

关键词：非视距量测;交互多模;多自主水下航行器;协同定位

近年来，多自主水下航行器(multiple autonomous underwater vehicles, MAUVs)协作系统实现了系统中各AUVs间的协调与信息交互，可有效地减少任务时间，提高工作效率，在海底勘探、水下侦查、目标搜索等方面有着广阔的应用前景。

MAUVs协同定位是在协作系统的基础上发展而来的一种新型定位方法，其利用水声通信技术，交换共享各自实时相对距离与方位信息进行融合，从而获得更高的整体定位精度[1]。当前在AUVs间水声通信带宽限制下，协同定位系统以领航-跟随式(leader-follower)结构为主，各AUVs间相对距离信息主要通过测量水声信号传播到达时间(TOA)，信号接收强度(RSS)等手段来获得，在实际复杂环境中，水声信号均会受到非视距(non line of sight, NLOS)传播的影响[2-3]，造成AUVs间较大的相对距离测量误差，进而影响MAUVs协同定位精度。

在未获得NLOS距离量测先验信息的基础上，文献[4-6]将NLOS量测误差作为残差未知量，重新构造定位方程，并分别利用二次规划、最小二乘及半定规划等最优估计算法进行求解。文献[7]通过在线均值与变量估计法设计了NLOS识别方法，有效减小了NLOS测量有偏误差，并将所得距离量测信息应用于移动目标跟踪算法中。在文献[8]中，假设NLOS测量未被识别的前提下，建立了距离量测变化模型，并将Kalman滤波算法应用于NLOS量测平滑过程中，获得了理想的距离量测信息。

目前，在已有的大多数MAUVs协同定位问题研究中，均理想化地假设AUVs间的距离量测为视距(line of sight, LOS)量测。针对此问题，本文基于双领航者的MAUVs协同定位系统，在无法实时识别LOS/NLOS量测的情况下，以4状态Markov链描述了定位过程中的LOS/NLOS量测模型转换过程，利用交互多模(interacting multiple models,IMM)理论设计了一种距离量测平滑算法，从而希望实现LOS/NLOS量测模型的自适应匹配，有效提高AUVs间的相对距离量测估计精度。

1问题描述

在实际海洋环境中，特别是浅海海域，由海面、海底及目标障碍物所引起的信号多径传输效应会对水声换能器之间的距离测量造成影响。研究发现[2]，在水下多障碍物环境中，由水下目标障碍物(如礁石、船壳等)所引起的信号非视距传播，相较于海面、海底及温跃层对信号的反射与散射，会造成更大且难以忽略的水声测距误差。当MAUVs协同编队在复杂环境下航行时，如图1所示。其中，领航AUV1与跟随AUV间为NLOS传播，由于障碍物的遮挡，信号从A点出发在B点经过折射才能传至C点(图中实线)，无法直线传播(图中虚线)，继而造成两AUVs间的量测距离大于实际距离；领航AUV2与跟随AUV间则可认为是LOS传播。

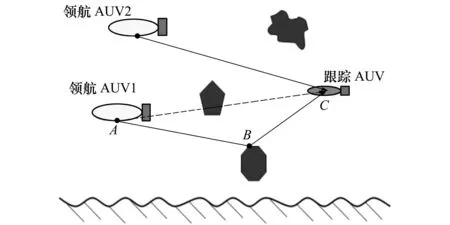
图1　MAUVs系统中的NLOS测距

利用水声信号传播延迟时间计算AUVs间距离，则领航AUVκ(κ=1,2)与跟随AUV在k时刻的距离量测为

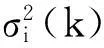
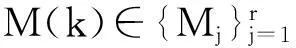
由于在实际MAUVs协同定位过程中，变量M(k)表示的量测模型所处条件很难被识别，因此需要设计相应的算法在LOS/NLOS混合条件下对AUVs间距离量测进行估计。

2NLOS量测平滑算法

2.1量测模型

在基于领航者的MAUVs协同定位系统中，可定义AUVs间距离量测估计的状态向量为

式中,v1(k)和v2(k)分别表示领航AUVs与跟随AUV间距离量测d1(k)和d2(k)的相应变化速度，从而其状态方程可表示为

式中，δt为采样周期，υ(k)为基于距离量测变化加速度的驱动噪声，并假设为零均值高斯白噪声。继而可简化(4)式为

根据距离量测(1)式，可定义LOS条件下的量测与噪声分别为rκ,LOS(k)、wκ,LOS(k)，NLOS条件下的量测与噪声分别为rκ,NLOS(k)、wκ,NLOS，假设NLOS修正偏差δm通过前期实验先验已知，且LOS条件下的距离偏差为0，从而可有

(6)

当AUVs间的距离量测所处条件为M1时,建立距离量测方程如下

(7)

可简化为

(8)

当距离量测所处条件为M2、M3及M4时,分别可得

(9)

且同样有

(10)

2.2基于IMM的量测平滑算法

交互多模(IMM)算法在给定系统模型集的前提下,使各个模型并行地进行独立滤波,并根据贝叶斯规则对各自估计结果作概率加权求和处理,从而求得系统状态估计。在NLOS量测平滑算法设计中,如图2所示,利用4个并行独立Kalman滤波器结合各自对应量测模型对状态向量θ(k)同时进行估计,分别根据估计所得误差通过似然函数同步获得各量测模型概率,继而联合各独立滤波器估计结果求得状态向量θ(k)的估计更新。整个量测平滑算法结构包括输入交互、模型匹配滤波及输出交互等3部分,其具体算法如下。

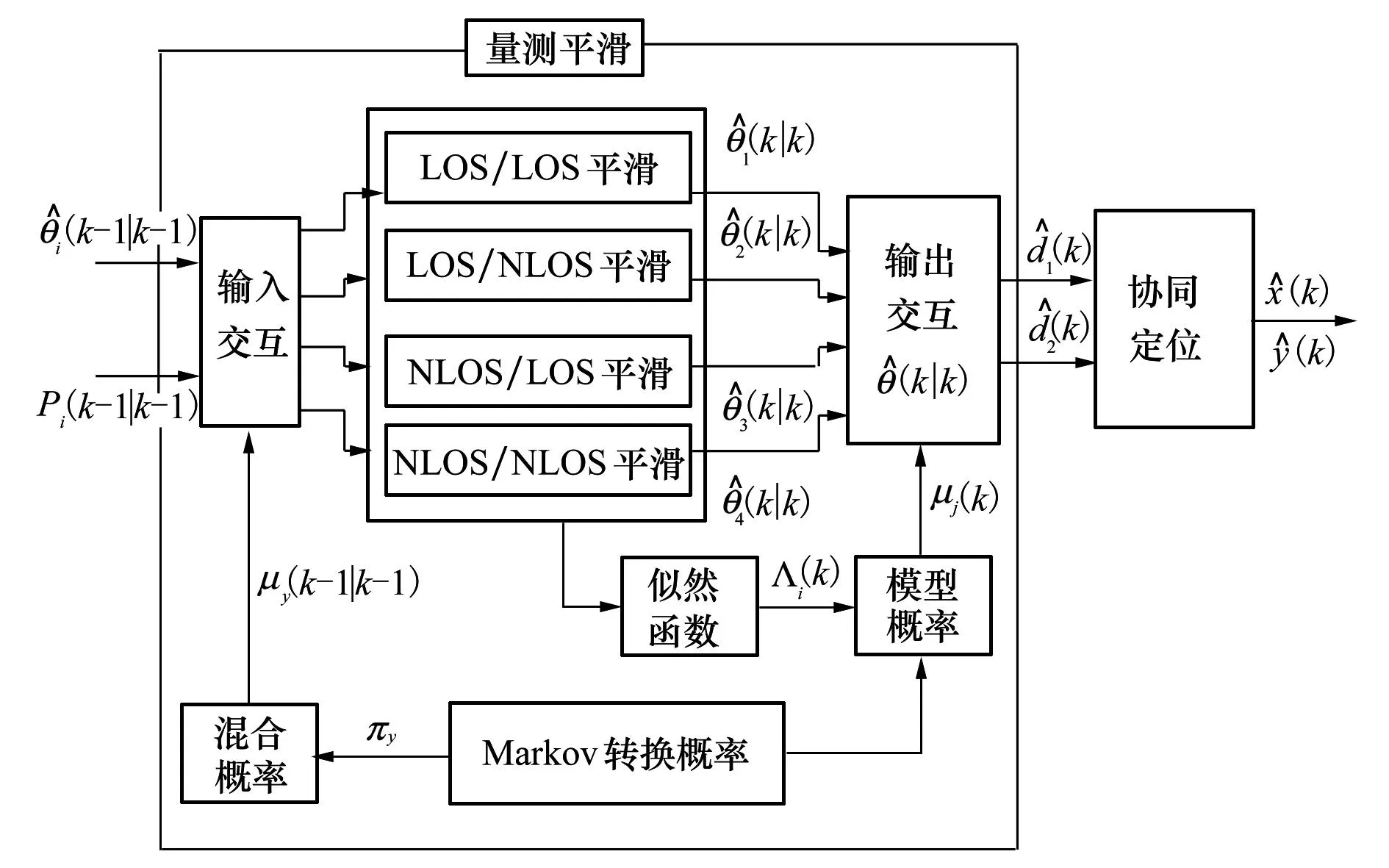
图2　距离量测平滑算法结构示意图

1)输入交互:∀i,j∈{1, 2, 3, 4}

假设量测模型间Markov转换概率πij已知,则模型i到模型j的混合概率为

(11)

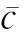
(12)

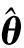
(13)

(14)

2)模型匹配滤波:∀j∈{1为LOS/LOS滤波器,2为LOS/NLOS滤波器,3为NLOS/LOS滤波器,4为NLOS/NLOS滤波器}

利用经典Kalman滤波设计4种量测模型下的滤波器,其状态一步预测及预测均方误差分别为

(15)

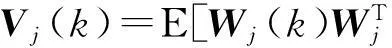
在多个模型匹配滤波器交互过程中,量测模型概率体现了各滤波器间的权重大小,k时刻量测模型j的概率可更新为

(20)

继而,利用各量测模型概率更新联合其相应模型匹配滤波器估计结果,可计算得状态向量估计及误差协方差矩阵分别为

最后,根据(3)式定义,可将估计所得状态向量中的距离量测值表示为

(26)

3仿真结果

为了验证文中所设计NLOS距离平滑算法的有效性,利用Matlab进行仿真分析研究。

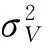
在MAUVs 协同定位过程中，给定量测模型间转换概率分别为: (1) 当i=j时，πij= 0.7; ( 2) 当i≠j时，πij= 0.1，其中NLOS量测占所有量测量的30%。如图4和图5所示。

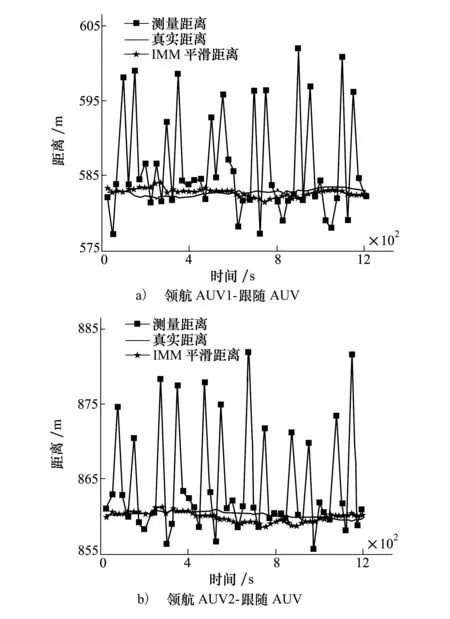
图4　修正偏差δm=14 m时领航与跟随AUV间距离

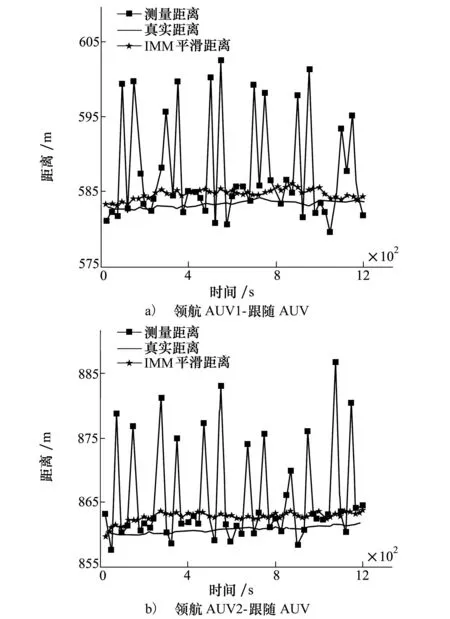
图5　修正偏差δm=9 m时领航与跟随AUV间距离

在NLOS量测的影响下,领航、跟随AUVs间的测量距离较之真实距离具有较大的正偏差;而在LOS量测随机噪声的影响下,领航、跟随AUVs间的测量距离同样会偏离真实量测,只是偏离幅度较小。在经过IMM算法进行平滑之后,领航、跟随AUVs间的测量距离误差大幅减小。继而,通过图4和图5对比可以发现,在不同NLOS修正偏差假设下,NLOS修正偏差越接近真实偏差,AUVs间的距离量测估计精度越高,越能贴近真实量测距离,反之亦然。

为了比较不同距离量测对MAUVs协同定位精度的影响,将图4和图5中相应的测量距离与IMM平滑距离应用于文中所设计协同定位算法中,并分别进行50次Monte-Carlo仿真求解对应均方根误差(RMSE)。其中,在k时刻的跟随AUV位置估计RMSE可表示为

(27)

(28)

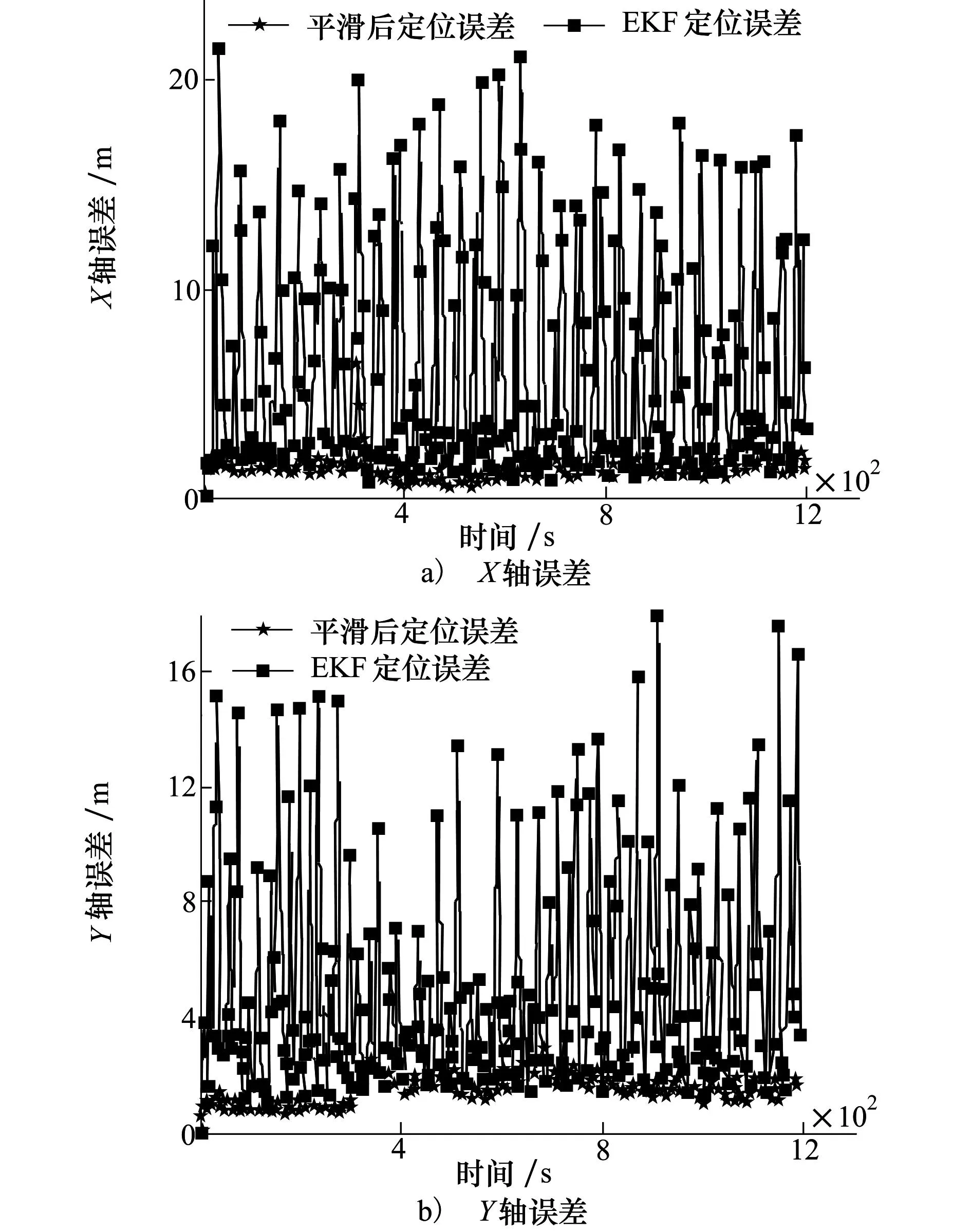
图6　修正偏差δm=14 m时跟随AUV协同定位误差

图7　修正偏差δm=9 m时跟随AUV协同定位误差

如图6和图7所示，受NLOS量测误差的影响，使用原始测量距离的协同定位误差具有较大幅度的波动。若使用经过IMM算法平滑后的估计距离，则可以有效的减小协同定位误差。比较图6和图7可以发现，与距离平滑估计结果相类似，MAUVs协同定位精度与NLOS修正偏差同样有关，NLOS修正偏差越接近真实偏差，测量距离估计越精准，随之得到的协同定位精度越高。

4结论

本文针对基于双领航者的MAUVs协同定位系统，在无法识别LOS/NLOS量测的情况下，以4状态Markov链描述了定位过程中的4种量测模型转换过程，并设计了一种基于交互多模(IMM)理论的距离量测平滑算法，有效地减轻了NLOS误差对AUVs间相对距离量测的影响，提高了跟随AUV定位性能。同时通过2组仿真实验发现，NLOS修正偏差越精准，则距离量测估计精度和协同定位精度越高。由于在算法设计中量测模型转换概率及NLOS修正偏差为初始给定恒值，因而，在进一步地研究过程中，提高算法的自适应性将成为新的研究方向。

参考文献：

[1]WillcoxS,GoldbergD,VaganayJ,CurcioJ.Multi-VehicleCooperativeNavigationandAutonomywithBluefinCADRESystem[C]//InternationalFederationofAutomaticControlConference(IFAC), 2006: 1-6

[2]DiamantR,TanH,LampeL.LOSandNLOSClassificationforUnderwaterAcousticLocalization[J].IEEETransonMobileComputing, 2014, 13(2): 311-323

[3]EmokpaeL,DiBenedettoS,PotteigerB,YounisM.UREAL:UnderwaterReflection-EnabledAcoustic-BasedLocalization[J].IEEESensorsJournal, 2014, 14(11): 3915-3925

[4]YuK,GuoY.ImprovedPositioningAlgorithmsforNonline-of-SightEnvironment[J].IEEETransonVehicularTechnology, 2008, 57(4): 2342-2353

[5]NawazS,TrigoniN.ConvexProgrammingBasedRobustLocalizationinNLOSProneClutteredEnviroments[C]//10thInternationalConferenceonInformationProcessinginSensorNetworks(IPSN), 2011: 318-329

[6]VaghefiR,BuehreeR.CooperativeSensorLocalizationwithNLOSMitigationUsingSemidefiniteProgramming[C]//9thWorkshoponPositioningNavigationandCommunication(WPNC), 2012: 13-18

[7]YuK,DutkiewiczE.NLOSIdentificationandMitigationforMobileTracking[J].IEEETransonAerospaceandElectronicSystems, 2013, 49(3): 1438-1452

[8]LiaoJ,ChenB.RobustMobileLocationEstimatorwithNLOSMitigationUsingInteractingMultipleModelAlgorithm[J].IEEETransonWirelessCommunications, 2006, 5(11): 3002-3006

A NLOS Measurement Smoothing Algorithm for Cooperative

Localization in Multiple Autonomous Underwater Vehicles

Ma Peng1, Zhang Fubin1, Tian Bing2, Xu Demin1

Abstract:In the process of MAUVs cooperative localization based on two leaders, in order to mitigate the influence of NLOS measurement deviation, a four state Markov chain is used to describe the switch process among four LOS/NLOS range measurement models which are independent of each other. Then we design a relative range measurement smoothing algorithm by combining the IMM and Kalman filter theory among AUVs, and the range measurement estimation results are applied to the MAUVs cooperative localization system. Simulation results and their analysis indicate preliminarily that the proposed algorithm does improve effectively the estimation accuracy of relative range measurement among AUVs. Moreover, the performance of the corresponding cooperative localization is also better than that of conventional method.

Key words:algorithms, autonomous underwater vehicles, computer simulation, covariance matrix, design, efficiency, errors, estimation, Kalman filters, Markov processes, mathematical models, MATLAB, mean square error, measurement errors, measurements, probability, trajectories; cooperative localization, interacting multiple models, multiple AUVs (MAUVs), non line of sight measurement

中图分类号：TP391

文献标志码：A

文章编号:1000-2758(2015)05-0854-06

作者简介：马朋(1987—)，西北工业大学博士研究生，主要从事水下协同导航研究。

基金项目：国家自然科学基金(61273333)资助

收稿日期：2015-03-04