全捷联导引头制导信息滤波算法及仿真
张韬, 张希铭, 王民钢
(1.西北工业大学 航天学院, 陕西 西安 710072;2.飞行控制与仿真技术研究所, 陕西 西安 710072)
全捷联导引头制导信息滤波算法及仿真
张韬1,2, 张希铭1,2, 王民钢1,2
(1.西北工业大学 航天学院, 陕西 西安710072;2.飞行控制与仿真技术研究所, 陕西 西安710072)
摘要:全捷联导引头存在制导所需的视线角速度信号不能直接测量的问题,基于无迹施密特卡尔曼滤波器(unscented Schmidt-Kalman filter,USKF)提出了一种全捷联导引头的制导信息提取算法。USKF对增广状态中的参数向量不进行校正,避免了参数观测误差过大对于滤波器性能的影响。在目标机动及制导律有落角约束要求的条件下,对制导信息提取算法进行了仿真验证。仿真结果表明,USKF滤波器性能优于传统非线性滤波器EKF及UKF,能够更准确地给出制导律所需信息,为全捷联导引头方案提供了理论基础及工程应用参考。
关键词:全捷联寻的制导;无迹施密特卡尔曼滤波;弹道成型导引律
许多现代战术导弹都采用了惯性稳定平台式的导引头,其跟踪及稳定回路中都少不了机械常平架。因此这种体制具有如下缺点:①系统可靠性不高,生产、装配、标定较复杂;②导致弹体的体积和质量大,造价较高;③跟踪系统性能、万向架摩擦等因素皆会影响视线角速率测量的准确性。
当代光电传感器技术不断进步,使得导引头光学系统的瞬时视场足够大,不再需要机械常平架,于是捷联导引头技术以及捷联寻的制导技术走向了实际应用阶段。得益于机械平台及连接部件的消失,导引头系统变得更加可靠。大的瞬时视场则使得视线跟踪角速率不再受到限制;由摩擦导致的俯仰、方位跟踪通道之间交叉耦合被有效消除;系统的结构复杂性下降,制造成本也随之降低。
当然,相对于经典的常平架体制导引头,全捷联导引头的寻的制导体制还存在如下困难[2]:
1) 光学系统必须有足够大的瞬时视场;
2) 无法直接测量制导所需视线角速度信号;
3) 大的瞬时视场会引入大的测量噪声。这将对整个制导系统的稳定性和精确性产生直接影响;
4) 必须采用数学平台来对弹体姿态对视线角的扰动进行解耦。
1捷联导引头制导信息滤波算法
1.1体视线角解耦为惯性系下视线角
设qIH、qIV分别为惯性系水平视线角和垂直视线角,qBH、qBV分别为弹体系水平视线角和垂直视线角,ψ、ϑ、γ分别为弹体偏航角、俯仰角和滚转角,通过坐标变换可得到解耦公式:
qIV=arcsin(sinθcosqBVcosqBH+
sinqBVcosθcosγ+cosqBVsinqBHcosθsinγ)
(1)
(2)
式中
M=-cosθsinψcosqBH+
tanqBV(sinθsinψcosγ+sinγcosψ)-
sinqBH(cosψcosγ-sinθsinψsinγ)
N=cosθcosψcosqBH+
tanqBV(sinγsinψ-sinθcosψcosγ)-
sinqBH(sinψcosγ+sinθsinψcosγ)
1.2弹目相对运动模型建立
1) 状态方程建立
本文假设目标为地面目标,并可作未知机动,取目标位置及速度值作为状态变量,状态初值可在发射时由载机装订:
(3)
取目标加速度作为参数向量:
(4)
取增广状态向量为:
(5)
则有状态转移方程:
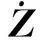
(6)
离散化状态转移方程:(T为滤波周期)
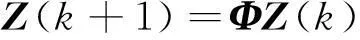
(7)
2) 观测方程建立
观测方程使用1.1中解耦后的惯性系下视线角作为测量值,即观测向量为:
(8)
由此可得观测方程:
(9)
1.3无迹施密特卡尔曼滤波器
USKF[3](unscentedSchmidt-Kalmanfilter)即无迹施密特卡尔曼滤波器。USKF基于UKF的框架,通过设定状态-参数增广矩阵来进一步考虑模型参数误差对于估计的影响。USKF并不需要将估计方程和参数方程分开,而是通过增广方式进行一次性计算。只是在最后的校正步骤时,参数估值并不进行校正。在传统UKF算法中,参数估值必须校正。然而USKF的优势在于,通常情况下参数不能很好地从测量值中被观测,因此对它们的估值进行校正可能使其较大的估值误差影响到状态估值的精度。USKF滤波计算步骤如下:
考虑增广后的状态向量及其方差矩阵:
(10)
式中,X为状态向量,C为参数向量。
1) 一步预测
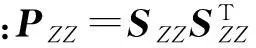
(11)
这里对于所有的i有:
(12)
2) 一步校正(此步运算将角标k省略)
系统量测值的Sigma点Yi=H(Zi,t),借此我们计算量测预测值、方差及增广的量测-状态协方差
(13)
(14)
(15)
接下来计算扩增卡尔曼增益:
(16)
由此得到一步校正,完成第k步的滤波运算:
(17)
(18)
1.4制导信息提取
使用USKF对增广状态向量进行估值后,对状态值做代数运算后可提取制导律所需信息:
弹目相对距离x、y、z向分量滤波值
(19)
弹目相对速度vx、vy、vz向分量滤波值
(20)
弹目相对距离的滤波值:
(21)
弹目接近速度的滤波值:
(22)
惯性视线角滤波值:
(23)
(24)
惯性视线角速率滤波值:
(25)
(26)
剩余飞行时间滤波值:
(27)
2带落角约束导引律
由于制导信息滤波算法为制导律提供制导信息,因此在没有制导律的前提下无法考察滤波算法的性能。为此我们采用了针对地面目标的带落角约束的导引律验证USKF算法的性能。
2.1弹目关系方程建立
一般弹目关系模型方程组:

(28)
(29)

(30)
式中:q为惯性系下视线角,r为弹目相对距离,at,am分别为目标和导弹的加速度,vt,vm分别为目标和导弹的速度,δ为导弹速度矢量与r的夹角,θ为目标速度矢量与r的夹角,y为弹目纵向距离:
方程组线性化后得到:
(31)
(32)
(33)
式中,tf为终端时间,tgo=tf-t,Vc=Vmcosδ-Vtcosθ。
2.2弹道成型导引律原理
借助2.1中的弹目关系线性化方程,考虑机动目标的制导系统状态方程为:
(34)
时变目标代价函数:
(35)
终端条件Dx(tf)=E,式中:
(36)
根据最优控制理论,可解得:
(37)
(37)式即广义最优弹道成型导引律,其中:
位置项系数NP=2(n+2)
落角项系数Nθ=(n+1)(n+2)
目标机动项系数NaT=(1-n)(n+2)/2
当n取1时,目标机动项为零:
(38)
考虑到目前的导引头硬件能力,目标加速度无法准确获得,因此我们认为(38)式相比较一般形式更具有实用价值。我们将此导引律选为本文所论述的制导系统方案的导引律。
3制导系统方案整体设计与仿真
3.1设计思路及示意图
结合前文所述制导信息滤波算法及最优导引律,我们对制导系统进行了整体设计,如图1所示:
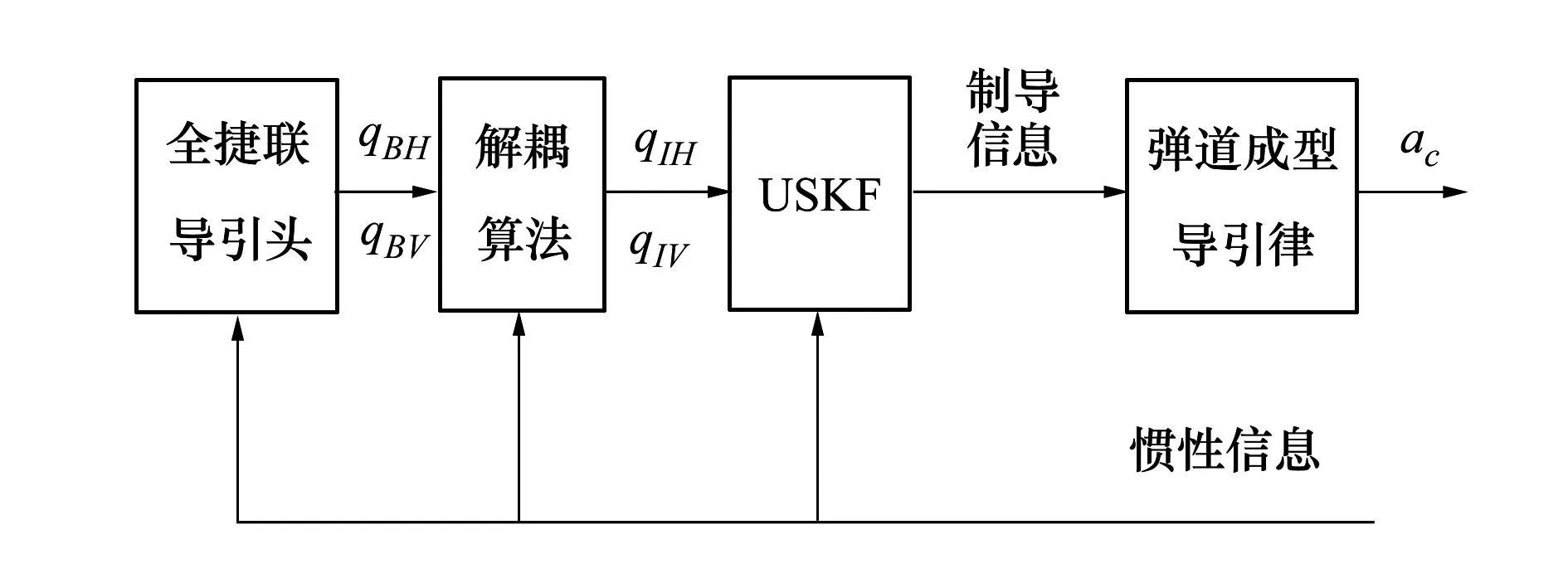
图1 制导方案示意图
由于制导末段必将进入导引头盲区,我们采取了剩余时间小于0.3s时保持制导指令不变的方案。
3.2仿真条件及结果
1) 单次打靶验证
假设末制导启动时导弹位置/m(0,1 000,0),目标位置/m(2 000,0,2 000),导弹初始速度/(m·s-1)(200,0,0),目标初始速度/(m·s-1)(10,0,10),目标机动情况为:
0~8s:ax=ay=az=0 m/s2
8 s以后:ax=2 m/s2,ay=0 m/s2,az=4 m/s2

图2 导弹与目标空间运动轨迹 图3 惯性系视线方位角滤波结果 图4 惯性系视线高低角滤波结果

图5 惯性系视线方位角速率滤波结果 图6 惯性系视线高低角速率滤波结果图7 剩余时间滤波结果
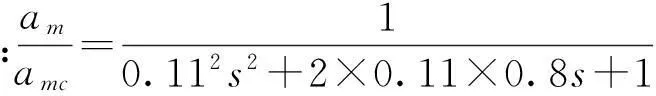
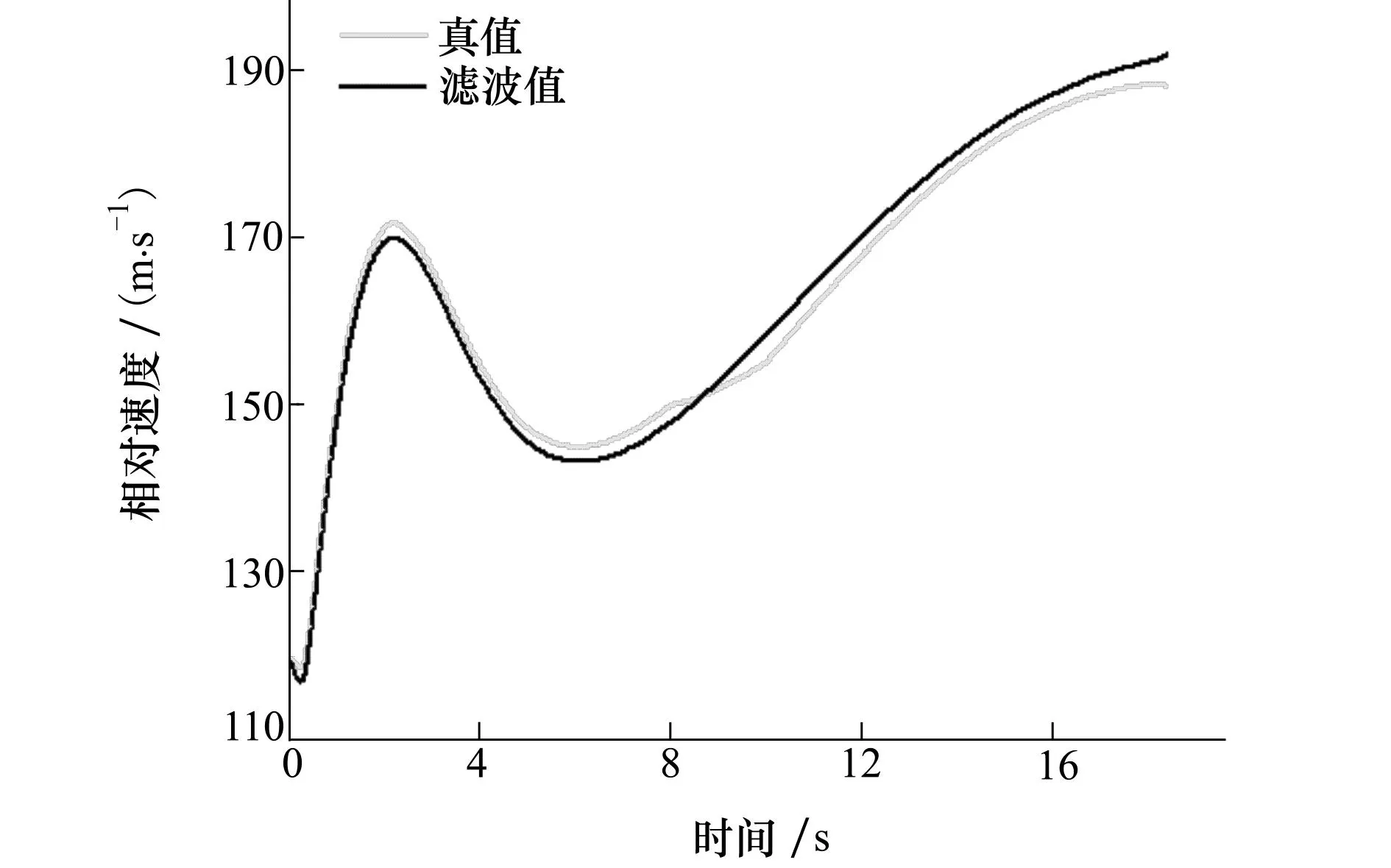
图8 弹目接近速度滤波结果
仿真结果:单次脱靶量0.834m,命中点落角为44.65°,各个制导信息的估计效果较好,所采用的制导系统方案能有效打击地面机动目标。
2) 蒙特卡罗打靶效果比较
我们选择了EKF、UKF作为对比,导引头噪声特性、导引律与飞控等效模型都是相同的,调整弹目初始距离,经过50次蒙特卡罗打靶得到如下结果:

表1 目标机动条件下50%脱靶量/m
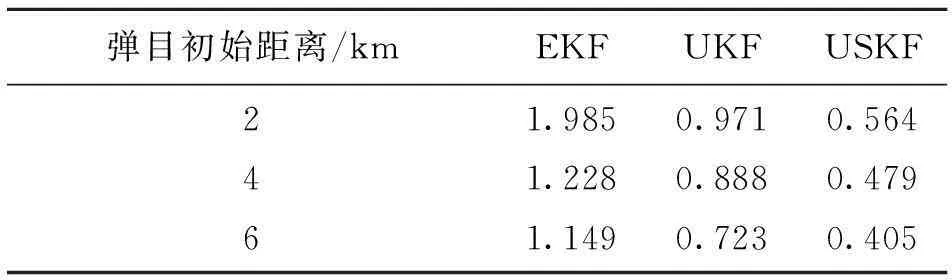
表2 目标不机动条件下50%脱靶量/m
对比仿真结果表明:在面对机动目标时,相比于传统非线性滤波器EKF及UKF,USKF算法能够显著改善捷联导引头信息滤波的精度,相应地改善了脱靶量,提高了制导系统的性能。
4结论
本文采用无迹施密特卡尔曼滤波器设计了一种全捷联导引头信息滤波方案,并选取了落角约束导引律进行了目标机动情况下的仿真验证。仿真结果表明,无迹施密特卡尔曼滤波器可以准确估计制导信息。将这些估值应用于落角约束型导引律,明显地增强了导弹的寻的导引能力,提升了其打击地面机动目标的命中精度和毁伤能力。
参考文献:
[1]王佩,张科. 跟踪-微分器在全捷联制导中的应用分析[J]. 西北工业大学学报,2014,32(5):817-821
Wang Pei, Zhang Ke. Application and Analysis of Tracking-Differentiator in Strapdown Guidance[J]. Journal of Northwestern Polytechnical University, 2014, 32(5): 817-821 (in Chinese)
[2]姚郁,章国江. 捷联成像制导系统的若干问题探讨[J]. 红外与激光工程,2006,35(1):1-6
Yao Yu, Zhang Guojiang. Discussion on Strapdown Imaging Guidance System[J]. Infrared and Laser Engineering, 2006, 35(1): 1-6 (in Chinese)
[3]Jason Stauch, Unscented Schmidt-Kalman Filter Algorithm[J]. Journal of Guidance, Control and Dynamics, 2015, 38(1): 117-123
[4]James M Maley. Line of Sight Rate Estimation for Guided Projectiles with Strapdown Seekers[C]//AIAA Guidance, Navigation, and Control Conference, 2015: 1-24
[5]Sreeja Hablani. Precision Munition Guidance and Moving Target Position Estimation[C]//AIAA Guidance, Navigation, and Control Conference, 2015: 1-21
[6]林德福,王辉. 战术导弹自动驾驶仪设计与制导律分析[M]. 北京:北京理工大学出版社,2012
Lin Defu, Wang Hui. Autopilot Design and Guidance Law Analysis for Tactical Missiles[M]. Beijing: Beijing Institute of Technology Press, 2012 (in Chinese)
Algorithm and Simulation for Guidance Information
Filter for Strapdown Seekers
Zhang Tao1,2, Zhang Ximing1,2, Wang Mingang1,2
西北工业大学尹士悦副教授被授予
“中国人民抗日战争胜利70周年纪念章”
本简讯根据《西北工大报》2015年9月16日第831期头版、记者王凡华写的“百岁抗战老兵看阅兵「胜利需要武器更需勇气”报道」。简讯改了标题,只名留了改写者认为最核心的内容,文字也改为正叙述。
尹士悦出生于1914年7月,1943年5月被派往美国学习并接收新型飞机。他曾参加滇缅公路保卫战,与美国飞虎队并肩作战轰炸日军机场。他说:“我当时负责领航和投弹。炸弹投下后,我看到日军的机场上,火光冲天,浓烟滚滚。我的心里特别高兴。……”。1948年冬,他脱离国民党空军,成为1名人民空军教官,先后荣立二等功和三等功。1954年10月,尹士悦转业到南京华东航空学院,成为人民教师。此后,在西北工业大学任讲师、副教授。1984年尹老光荣离休。
9月3日同学们来到老人家中,陪同老人观看阅兵。老人激动地与同学们讲起自己抗击日寇的战斗情景,讲述了送中国代表团到东京,参加远东国际军事法庭审判日本战犯时的情况……。


Abstract:Problem exists in strapdown seekers that the line of sight rate cannot be directly measured, which is used for homing guidance. This paper develops an algorithm for strapdown seeker guidance information filtering based on unscented Schmidt-Kalman filter(USKF). The USKF does not correct the parameters in augmented state vector, thus avoiding performance reduction duo to large estimation error of parameters. We conducted simulations to verify the guidance information filtering algorithm, assuming maneuvering target and guidance law with constrained impact angle. Results and their analysis show preliminarily that USKF performs better than EKF and UKF, both traditional nonlinear filters, and gives more precise guidance information, thus giving engineering reference for strapdown seeker system design.
Key words:angular velocity, cost reduction, data processing, guidance systems, Kalman filters
中图分类号:TJ765.3
文献标志码:A
文章编号:1000-2758(2015)05-0744-06
作者简介:张韬(1990—),西北工业大学硕士研究生,主要从事导弹制导及控制研究。
收稿日期:2015-04-16

