Stolz定理应用探讨及相关问题

翟金成，蒋妍

（1.郑州幼儿师范高等专科学校；2.郑州旅游职业学院，河南郑州450000）

Stolz定理应用探讨及相关问题

翟金成，蒋妍

（1.郑州幼儿师范高等专科学校；2.郑州旅游职业学院，河南郑州450000）

本文首先给出了Stolz定理的推广形势及其证明，其次给出了它在证明L’Hospital法则及求待定型数列极限上的一些应用，最后又利用它研究了具有非线性递推关系数列的渐进性。

Stolz定理；L’Hospital法则；待定型.

引言

Stolz定理是数学分析中处理待定型数列极限一个非常有效的工具。在本文中我们将会给出推广的Stolz定理及其证明，最后还将给出它在证明L’Hospital法则等方面的应用。

一、推广的Sto lz定理及其证明

为了便于比较，我们首先不加证明的给出Stolz定理.

Stolz定理2（⍛º型）..设{an}是趋向于零的数列，{bn}是严格单调递减趋于零的数列，如果

推广的Stolz定理1.

设T为正常数，若函数g（x），g（x）,x∈［a,＋∞）满足：

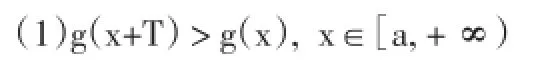
（2）Lim g（x）=＋∞，f(x),g(x)在［a,＋∞）的任意子区间上有界；

证明：不妨设g（x）＞0,x∈［a,＋∞）。由（3）及极限定义容易推知，对任意给定的∈＞0，必有正数A＞a，使对一切x∈[A,A+T]及一切自然数P有

上述各式相加有

利用(4)的右边不等式可得

由于显然f(x),g(x)在[A,A+T]中有界，当P→+∞时g(x+PT)关于x∈[A,A+T]一致趋于+∞故存在正整数P。使

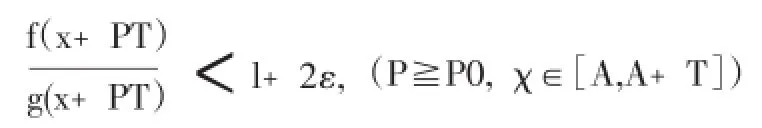
于是对一切y≥A0＝A+P0，恒有

于是

推广的Stolz定理2（⍛º型）.

设T为正常数，若函数g（x）,f（x）,x∈［a,+∞）满足

（1）0＜g（x＋T）＜g（x）,x∈［a,+∞）

（2）lim g(x)=0,lim f(x)=0；

证明：和上述定理中（4）式类推可得：对任意给定∈＞0，必有正数A＞a，使对一切x∈[A,A+T]自然数P都有

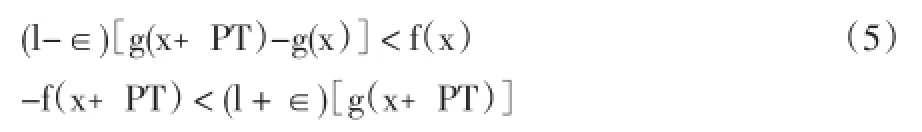
（注意，这里与（4）式不同的是与以及与的位置调换了。）

对任意固定的x＞A，我们在（5）式中令P→+∞，由于

lim g(x+PT)=lim f(x+PT)=0，故得

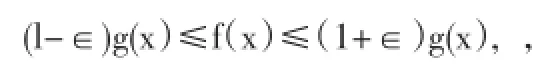
对于l=+∞,-∞的情形结论仍真。

利用推广的Stolz定理证明L’Hospital法则

设g'(x)≠0,x∈[a,+∞)，lim g(x)=+∞，lim则

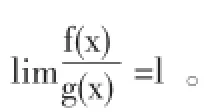
证明：只须验证ƒ（x）及g（x）在[a,+∞]上满足推广的Stolz定理1的一切条件即可。这里T=1.

首先，由于g'(x)≠0,x∈[a,+∞)，由Darboux定理我们知g'(x)≠0,在[a,+∞)内恒不改变符号，再因为条件给出lim g(x)=+∞，所以g'(x)＞0,x∈[a,+∞)，然后验证条件：

（1）利用Lagrange公式，对任意的x∈[a,+∞)，有θx∈(0,1)，使g'(x)≠0,x∈[a,+∞)，

（2）由于g'(x+θx)＞0，故g(x+1)-g(x)＞0，

或即g(x+1)＞g(x)，x∈[a,+∞)。

（3）由条件，ƒ（x）在[a,+∞]上可导，故ƒ（x）在[a,+∞]的任意子区间上有界，lim g(x)=+∞已由条件给出。

（4）由Cauchy公式，对任意的x∈[a,+∞)，有θx∈(0,1)，使

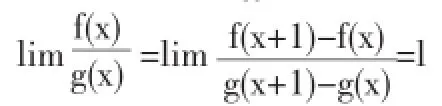
b)（⍛º型）的L’Hospital法则.

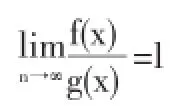
证明可仿照1的证明。

三、Stolz定理在求待定型数列极限上的应用

例设级数∑an收敛，又{Pn}为单调增加的正数列，且Pn→+∞(n→+∞)证明

四、Stolz定理在研究数列渐进性方面的应用

结论：设a＞0,p＞1,取x。为正数使得0＜ax0p-1＜1令 xn+1=xn-axpn，那么有换个写法就是

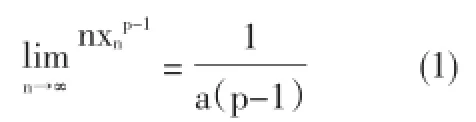
证明：首先，易知limn∞→xn=0再有Stolz公式和L`Hospital法则，我们有

[1]裴礼文.数学分析问题中的典型例题和方法[M].高等教育出版社，2001.

[2]舒阳春.高等数学中的若干问题解析[M].科学出版社，2005.

O171

A

1674-6198（2015）03-0078-02

2015-03-12

翟金成（1981-），男，河南工业大学讲师，硕士研究生，主要研究方向：数学理论与应用；蒋妍（1978-），女，郑州旅游职业学院讲师，硕士，主要从事数值优化、图像处理方面研究。