自学习粒子群与梯度下降混杂的漏磁反演方法*

韩文花，徐俊，沈晓晖，吴正阳

（上海电力学院自动化工程学院，上海200090）

自学习粒子群与梯度下降混杂的漏磁反演方法*

韩文花，徐俊，沈晓晖，吴正阳

（上海电力学院自动化工程学院，上海200090）

利用自学习粒子群优化算法的全局寻优能力克服梯度下降法过分依赖初始解，易陷入局部极值的缺点，从而提高梯度下降法的优化性能。以径向基函数神经网络为前向模型，基于自学习粒子群与梯度下降混杂的反演方法用于漏磁缺陷轮廓重构中。实验结果表明，该反演方法重构的缺陷轮廓比较准确，且在漏磁信号存在噪声的情况下，重构结果到与实际轮廓相近，并具有一定的噪声鲁棒性。

漏磁检测，反演方法，粒子群优化，梯度下降法

0 引言

漏磁检测作为一种重要的无损检测方法，具有对使用环境要求低、检测速度较快、可实现缺陷的定量化评价以及可以发现一定深度的缺陷等优点，在工程实践中得到了广泛的应用［1］。漏磁检测针对的测量对象是由铁磁性材料制作而成的军用装备［2］、风电场设备［3］、石油管道［4］等。由于处于复杂恶劣的环境中，这些设备或设施容易出现腐蚀、裂纹等缺陷，给正常的生产运行带来巨大的安全隐患。为了避免不必要的损失和事故，需对其进行定期检测［5］。

在漏磁检测中，缺陷轮廓重构是指根据由传感器采集所得的漏磁信号求得缺陷的轮廓信息，也就是将缺陷进行定量化。缺陷轮廓重构一般使用的是反演方法，反演方法分为两大类：基于模型和非模型的反演方法。非模型反演方法通过信号处理技术直接建立信号与缺陷几何形状的关系实现重构，其中典型的有应用神经网络建立函数关系，这类方法处理快速，但受限于神经网络训练时的缺陷尺寸范围［6］。而基于模型的反演方法是指建立一个物理模型（即前向模型），可以将漏磁信号转化成缺陷轮廓信息，再使用迭代方法等不断最小化由前向模型输出的漏磁信号与测量漏磁信号之间的差值，最终所求的解则为重构的缺陷轮廓。梯度下降法（Gradient Descent，GD）已经作为迭代算法应用于漏磁反演方法中并取得了良好的重构效果［7］，但由于梯度下降法中本身的缺陷，使得其性能严重受限于该算法的初始解。若其初始解远离真实缺陷轮廓，就会导致其收敛缓慢，甚至陷入到局部极值中。

为了解决初始解对梯度下降法性能的影响，本文将自学习粒子群优化算法（Self-learning Particle Swarm Optimization，SLPSO）［8］引入到梯度下降法中。SLPSO为改进型PSO，包含4种速度更新模式、自学习机制和维度更新，提高了PSO的优化性能。将SLPSO迭代优化所得的解作为梯度下降法的初始解，以缩短其运行时间，从而提高重构效率。

1 SLPSO

不同于许多只结合全局最优位置（gbest）和个体最优位置（pbest）更新粒子速度，SLPSO采用自学习机制从4种速度更新模式中选取最合适的一种，从而应对不同的情况。SLPSO中，在每次迭代的最后部分都需要对gbest进行维度更新，进而更新了gbest的存档位置（abest），所以粒子每个维度的有用信息都能有效利用。

1.14 种速度更新模式及自学习机制

位置pbest和gbest是最常用的两种速度更新变量，在PSO速度更新中有着重要的作用，pbest有利于PSO进行局部搜索，而gbest有利于PSO全局收敛，所以不过分依赖两者中的任何一个是十分有必要的。如果每次都同时使用pbest和gbest，反而可能抑制两者的优点。此外，适应度函数在不同的取值范围其变化趋势也会不同，所以在不同情况需使用不同的变量更新粒子速度。SLPSO针对开发pbest附近区域、跳出局部极值、探索新区域和收敛于gbest附近区域等4种不同情形，引入了4种速度更新公式。

1）开发pbest附近区域：

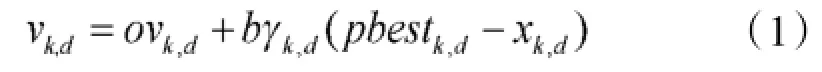
2）跳出局部极值：

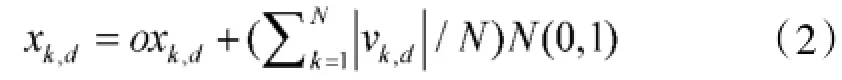
3）探索新区域

4）收敛于gbest附近区域

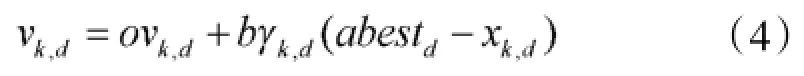
其中vk，d为第k个粒子第d维度上的速度；N为粒子种群大小；pbestrand，d为一随机粒子的pbest第d维度上的位置；N（0，1）为服从标准正态分布的随机值；b为学习因子，o是惯性权重，γ为选择概率允许的最小值。

为了选择最合适的更新公式，SLPSO采用了一种自学习机制。具体而言，每一种速度更新公式都有随迭代次数不断变化的选择概率，通过概率匹配方法选择其中一种，即结合下一代适应度、当代成功率和前代选择概率计算公式选择概率，因此，由速度更新公式带来的适应度值变化越大，这种更新公式就更可能被选择，从而每个粒子能够使用有效的更新公式进行更新。

在说明选择概率之前，需引出增进值和奖励值。

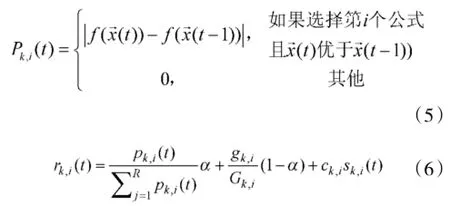
其中Pk，i（t）为第k个粒子对第i个速度更新公式的增进值；rk，i（t）为奖励值；f为适应度函数；α为从0到1均匀分布的随机值；gk，i为从最后一次选择概率更新起，第k个粒子使用第i个更新公式后成功学习的次数；Gk，i为第i个速度更新公式被选择的次数；sk，i（t）则为选择概率；ck，i为惩罚因子。

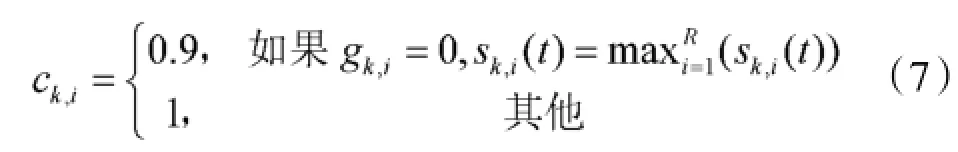
通过奖励值，则可更新选择概率。

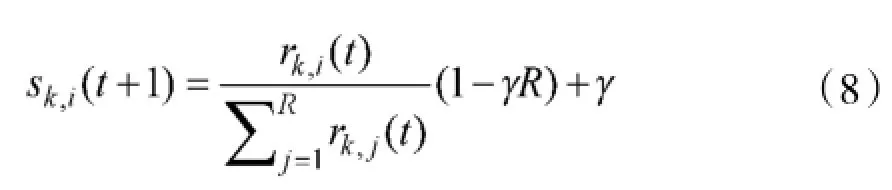
其中，R为速度更新公式的个数。

通过上述公式计算得出速度更新公式的选择概率，每个粒子都能够在每次迭代时选择出最佳的更新公式。此外，mk定义为第k个粒子连续未成功学习次数，如果mk超过最大阈值（Uf），则4个更新公式的选择概率都需要同时更新且mk初始化为0。

1.2 维度更新

对于大多数改进型PSO而言，如果某个粒子的更新位置要优于gbest，那么该更新位置就会取代gbest所有维度上的值。这种方式最明显的缺点是所有维度上的有用信息未得到充分的利用。实际上，真正所期望的信息往往只是几个维度上的。为此，SLPSO引入了abest，如果某个粒子更新完后的位置优于原先位置，则更新完后位置的某些维度很有可能含有有用信息，因此，abest就应充分检查每个维度的信息。具体而言，每一次都将更新完后位置的一个维度上的值替代abest对应维度上的，如果组合成的新位置要优于原先abest值，就证明了那个维度上的信息是有用信息，保留新产生的abest，直到所有维度都利用完毕。但这种检查有用信息的方式是十分耗时的，所以使用学习概率（P1）判断每个维度上的值是否需要调用abest进行有用信息检查，SLPSO从而节约了许多计算资源，提高了运行效率。

此外，对于许多优化问题如多峰问题，相对收敛于abest，各个粒子更应该搜寻局部区域，这样更有可能找到全局最优。而4种更新公式都促进了粒子群收敛，这样就不能保持有利收敛到abest的更新公式与其他3个的平衡，所以要控制能够调用最后一个更新公式的粒子个数。SLPSO在每次迭代都更新能够调用第4种更新公式的粒子数，奖励值、成功率和选择概率也同时更新。图1为SLPSO算法的流程图。

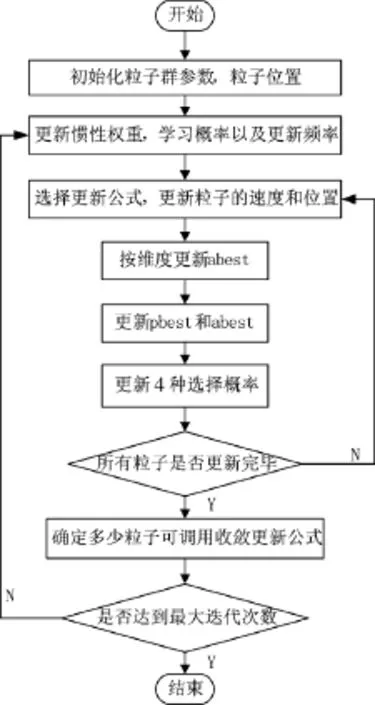
图1 SLPSO的流程图

2 SLPSO与GD混杂的漏磁反演方法

基于SLPSO和GD的漏磁反演方法，以径向基函数神经网络（Radial Basis Function Neural Network，RBFNN）作为前向模型，将指定缺陷轮廓转化成漏磁信号，SLPSO提供反演迭代开始之前的初始解，也就是GD的起始解，预测解在GD迭代的过程不断地接近实际缺陷轮廓，直到达到最大迭代次数或者预测解经过前向模型的输出漏磁信号与实际漏磁信号的差值达到要求，其流程图如图2所示。

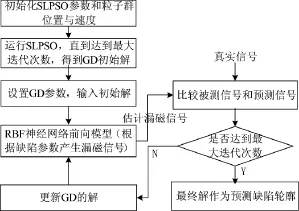
图2 基于SLPSO和GD的漏磁重构反演方法流程图

使用该反演方法之前，先训练RBFNN。使用前向模型估计的漏磁信号与实际漏磁信号的误差平方和作为两者差异的评估标准，同时该函数也作为SLPSO的适应度函数。

其中，M为漏磁缺陷的维度，也就是采样点数；P=［p1p2…pM］为实际漏磁信号，即由传感器采集到的信号；Y=［y1y2…yM］为RBFNN前向模型估计的漏磁信号。

在该反演方法中，使用梯度下降法更新预测的缺陷轮廓，最小化式（9）的函数值，每次迭代解的更新公式如式（10）所示。

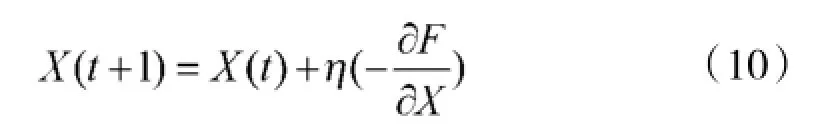
其中，X（t）为GD第t次迭代的解，其维度与缺陷轮廓采样点等同，即X（t）=［x1（t），x2（t），…，xN（t）］；η为学习速率，决定了GD的收敛速度；当GD达到最大迭代次数或者GD解的函数值F低于预设的阈值时迭代结束。

由于所用前向模型为RBFNN，且RBFNN的径向基函数使用的是高斯函数，如式（11）所示，所以可由式（12）得出F的偏导。

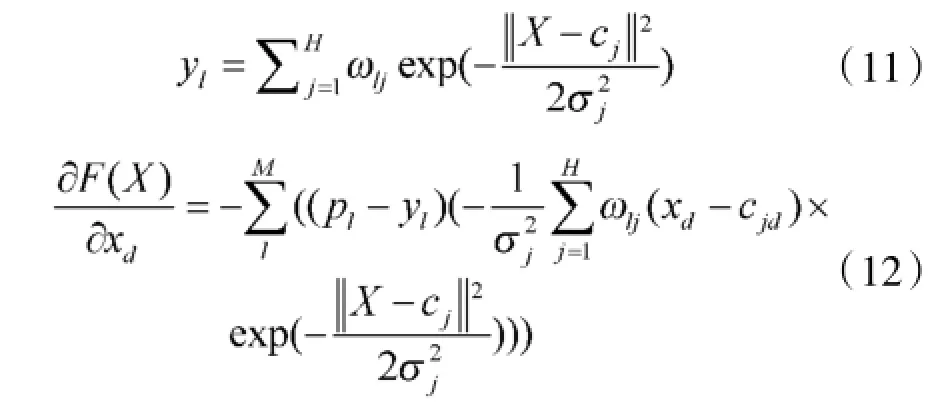
其中，H为使用的高斯函数个数；ω为与每个基函数相关的权值；c为高斯函数的中心。

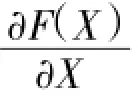
3 实验结果

为了验证基于SLPSO与GD混杂的漏磁反演方法的有效性，使用了240个缺陷轮廓-漏磁信号样本对。其中210个用于训练RBFNN，其余30个用来验证反演效果。这些缺陷都是矩形的二维缺陷，其深从0.15 in到0.85 in，宽从1 in到7 in。RBFNN的输入层节点个数等同于缺陷轮廓的采样点数，输出层节点个数等同于漏磁信号的采样点数，均为100个。本文分别采用不含噪声和含5%均匀噪声的漏磁信号进行漏磁反演，这样既可以验证该反演方法的重构能力，又能够判断其对噪声的鲁棒性。

图3给出了深0.7 in、宽2.2 in的缺陷轮廓重构结果，其中实线为实际轮廓，虚线为不含噪声的漏磁信号重构的轮廓，点划线为含5%噪声的漏磁信号重构出的轮廓，从图上可以看出，含噪声的信号重构出的轮廓与实际轮廓相近，精度与不含噪声的轮廓相差不大。见图4～图6。与图3类似，不含噪声的漏磁信号重构的轮廓更接近实际轮廓，比含噪声的信号重构的轮廓更加准确，这是因为漏磁信号中的噪声对该反演方法的影响，但含噪声的漏磁信号重构的轮廓总体上比较接近实际轮廓，因此，可表明基于SLPSO与GD混杂的漏磁反演方法对噪声具有一定的鲁棒性。

4 结论

为了解决梯度下降法对初始解的依赖性、易陷入局部极值等缺点，本文引入自学习粒子群优化算法，通过该方法的优化为梯度下降法提供一个与最优解相近的初始解，从而提高了梯度下降法的优化效率和性能。此外，本文将这种基于自学习粒子群与梯度下降混杂的反演方法用于漏磁缺陷重构中，成功地实现了缺陷轮廓的重构，且具有一定的噪声鲁棒性。

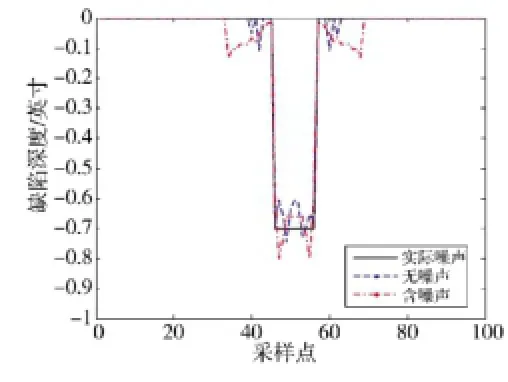
图3 深0.7 in、宽2.2 in的缺陷重构轮廓

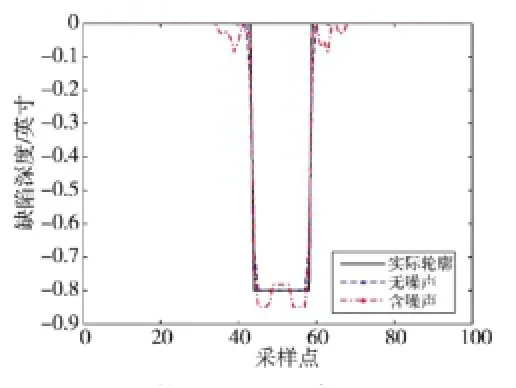
图4 深0.8 in、宽3.0 in的缺陷重构轮廓

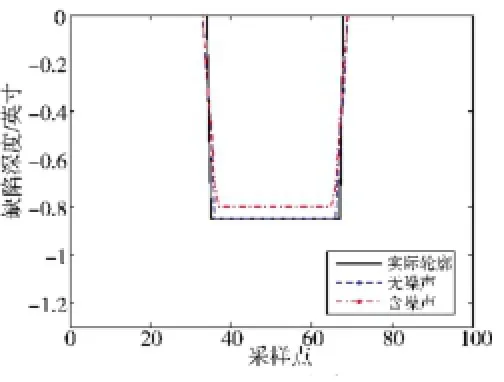
图6 深0.85 in、宽6.6 in的缺陷重构轮廓

［1］张卫民，杨旭，王珏，等.基于霍尔元件阵列的缺陷漏磁检测技术研究［J］.北京理工大学学报，2011，31（6）：647-651.

［2］雷良金，王长龙，孙世宇，等.基于蚁群算法的径向基网络漏磁信号二维反演［J］.火力与指挥控制，2011，36（3）：163-165.

［3］丁松，田贵云，王平.风力发电设备无损检测技术研究［J］.无损检测，2011（11）：37-41.

［4］Ireland R C，Torres C R.Finite Element Modelling of a Circumferential Magnetizer［J］.Sensors and Actuators，A: Physical，2006，129（1-2）:197-202.

［5］Priewald R H，Magele C，Ledger P D，et al.Fast Magnetic Flux Leakage Signal Inversion for the Reconstruction of Arbitrary Defect Profiles in Steel Using Finite Elements［J］. IEEE Transactions on magnetics，2013，49（1）:506-516.

［6］Maryam R，Reza K A，Slawomir K，et al.Sizing of 3-D Arbitrary Defects Using Magnetic Flux Leakage Measurements［J］.IEEETransactionsonmagnetics，2010，46（4）: 1024-1033.

［7］Pradeep R，Lalita U，Satish S U.Electromagnetic NDE Signal Inversion by Function-Approximation Neural Networks［J］. IEEE Transactions on Magnetics，2002，38（6）:3633-3642.

［8］Li C H，Yang S X，Nguyen T T.A Self-Learning Particle Swarm Optimizer for Global Optimization Problems［J］. IEEE Transactions on Systems，man，and Cybernetics—part B:Cybernetics，2012，42（3）:627-646.

Hybrid of Self-learning Particle Swarm Optimization and Gradient Descent Based Magnetic Flux Leakage Inversion

HAN Wen-hua，XU Jun，SHEN Xiao-hui，WU Zheng-yang
（College of Automation Engineering，Shanghai University of Electric Power，Shanghai 200090，China）

Byusingtheglobaloptimizationabilityofself-learningPSO，overcomethe disadvantages of gradient descent method unduly relying on initial solution and easy falling into local minimum，thereby the optimizing performance is enhanced.Radial basis function neural network is used as forward model，and the inversing approach based on the hybrid of self-learning PSO and gradient descent is applied to reconstruction of defect profile on magnetic flux leakage.The experiment results show the profiles reconstructed by the proposed approach are relatively accurate and still close to the true profile with existence of noise in magnetic flux leakage signal.So the proposed approach is partly robust to noise.

magnetic flux leakage inspection，inversion approach，particle swarm optimization，gradient descent

TP73

A

1002-0640（2015）01-0088-04

2013-11-10

：2014-02-23

国家自然科学基金资助项目（51107080）

韩文花（1976-），女，山东日照人，副教授。研究方向：无损检测，智能优化算法，信号处理等。