基于混合遗传算法的杂货船装载优化问题

朱莹，向先波，杨运桃

1华中科技大学船舶与海洋工程学院，湖北武汉430074

2中国船舶工业系统工程研究院，北京100094

基于混合遗传算法的杂货船装载优化问题

朱莹1，向先波1，杨运桃2

1华中科技大学船舶与海洋工程学院，湖北武汉430074

2中国船舶工业系统工程研究院，北京100094

杂货船的装载问题属于典型的三维装箱问题，在分析杂货船装载问题的特点的基础上，以船舱空间利用率最大为目标，建立杂货船装载问题的数学模型。针对模型特点，提出一种结合启发式算法和遗传算法的混合遗传算法，设计一种新的三空间划分方法，并对此算法进行仿真试验验证。以文献［3］的一组经典测试数据为实例，经与同类装箱问题中的同类型算法进行对比分析，发现空间利用率达到了92.94%，与其他算法的结果相比具有明显的优势，验证了优化算法的有效性。

杂货船；三维装箱；启发式算法；遗传算法

0 引 言

杂货船是一种运载包装、箱装、捆装、桶装货物的货船，其装载效率与运输成本直接相关，提高船舱的利用率可以在很大程度上节约运输成本。可以将杂货船的装载问题简化成一般的装箱问题。

装箱问题属于NP-Hard问题，研究的重点在于要根据特定的问题建立数学模型和寻求有效的求解算法。在实际应用中，精确数值计算方法的探讨已逐渐消失，取而代之的是启发式算法、模拟退火算法、禁忌搜索算法和遗传算法等各种智能算法在该问题求解过程中的大量应用［1］。本文拟采用混合遗传算法的启发式算法对杂货船的装载问题进行优化。

国内外对装箱问题已有一些研究，但主要针对的是二维装箱问题，有关三维装箱问题方面的研究较少。国外最有代表性的就是George和Robinson［2］提出的启发式算法，并且首先引入了层的概念。Loh和Nee［3］研究的启发式算法主要针对的是弱异类问题，其采用装填密度作为目标函数，构建水平层来由下至上装载，此外，其给出的15组测试数据经常被后人作为检验算法的经典数据。Bischoff等［4］提出的启发式算法主要针对的是货物装盘的问题，但和装箱问题有很多的相通之处。Bischoff和Ratcliff［5］提出的启发式算法考虑了多目的地运送的情况，其不是构建层而是通过构建柱来实现装载。Gehring和Bortfeldt［6］提出了一种比较典型的混合遗传算法，其将启发式算法与遗传算法相结合，提出了塔的概念，并将二维装填问题的思路引入到了三维装载问题中。国内比较有代表性的是何大勇等［7］提出的遗传算法，其通过权重系数变化法来处理多目标问题，通过罚函数法处理约束，并对多目标多约束装箱问题进行了研究。翟钰等［8］提出的启发式算法中，是由完全相同的货物组成块，然后用块自底向上依次填充的方式来完成装载，装载过程中，采用树搜索策略寻找最优的装载方式。陈德良等［9］设计了一种智能启发式算法，通过模拟人们在实际装箱时总是尽量保证每一层装的比较“平直”的思想，借以克服一般启发式算法依赖“经验”的不足。

启发式算法凭借实践经验建立搜索策略和搜索规则，并以此规则在搜索空间中求解，该算法被大量应用于装载问题中。但启发式算法在同一问题的不同实例中会产生不同的效果，这种不稳定性使得计算结果变得不可信。为了降低这种不稳定性，本文拟将遗传算法作为搜索算法来改进启发式算法，通过启发式算法确定装载规则来产生可行解，然后应用遗传算法在解空间中搜索令人满意的优质解。一般的优化算法［10］往往是直接利用决策变量的实际值来进行优化计算，而遗传算法则是以决策变量构造的编码为运算对象，更适合很难有数值概念的装载问题。遗传算法同时使用多个搜索点的搜索信息进行群体优化，这种特有的并行性使其搜索效率高于一般算法。遗传算法属于一种概率搜索技术，其选择、交叉和变异运算都是以一定的概率发生的，增加了搜索的灵活性。

一般的启发式规则多参考George和Robinson的思路［2］，引入层的概念，把装载过程当作一层一层的装入，这种思路与实际的装载过程非常契合。一旦空间中装入一个货物后，货物的周围就产生了三个剩余的空间，然后以一定的遍历方式选取优先级较高的货物进行装填，先是在层中摆满一条，再摆另一条，直至形成一个层。本文的启发式规则将参考George和Robinson［2］的思路并给予一些改进。本文拟将同种货物采用同一种放置状态，并尽量放在一起，以避免同种货物放在一起因放置状态不一致而产生空隙，从而提高一定的装箱效率；采用一种多样化的空间划分方式，针对不同的放置位置设计不同的空间划分方式，以有效避免一定的空间损失。同时，还将待装空间与相邻的废弃空间进行合并，使废弃空间得到再利用，从而提高空间利用率。

1 装载模型建立

1.1 问题描述

杂货船的装载问题可以描述为：将具有一定重量、体积、价值的不同种类、不同数量的物品按照一定的规则装入具有一定载重和容积限制的船舱内的过程，在满足运量限制的情况下实现箱内物品价值总和最大化。

1.2 约束条件和目标函数

杂货船装载优化的思路是根据不同的约束条件和目标函数构建不同的模型，然后再根据这些模型设计合适的算法进行求解，完成装载问题的优化。所以，要优化杂货船的装载问题，首先需要分析其约束条件和目标函数。

1.2.1 约束条件

在杂货船装载问题的描述过程中，一般具有以下几种约束条件：体积约束、载重约束、方向约束、承载能力约束、配装优先级约束和稳定性约束。本文主要考虑体积约束条件下的装载问题优化。

1.2.2 目标函数

杂货船装载问题的目标可选用1个或多个，一般选用的目标函数如下：

1）船舱的载重量利用率最大。

2）船舱的空间利用率最大。

3）船舱的面积利用率最大。

4）运输成本最低。

本文以船舱的空间利用率最大为目标函数。

1.3 模型假设

本文仅考虑单个船舱装载时的优化，不考虑特殊约束条件下的装载问题，并将以船舱的空间利用率最优为目标，构造杂货船装载问题的模型。为方便研究，做以下假设：

1）所有货物都可装入。

2）杂货船的载重量足够大。

3）货物均可以任意摆放。

4）货物无优先级。

5）货物包装箱体的强度足够。

6）货物的外形为规则矩形。

7）忽略装载对杂货船稳定性的影响。

8）货物之间的空隙用填充物填充以保证稳定，忽略装载中货物的稳定性因素。

1.4 模型的建立

杂货船的装载问题模型可以描述为：在满足船舱容积约束的条件下，确定各货物在船舱中的装载位置和放置状态，以使船舱的空间利用率最优。

本模型采用的坐标系是三维笛卡尔坐标系，如图1所示。该坐标系的X轴表示船舱的长度方向，Y轴表示船舱的宽度方向，Z轴表示船舱的高度方向。船舱的左下角为坐标系原点。

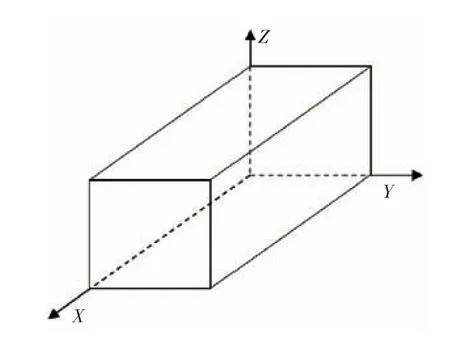
图1 坐标系Fig.1 The coordinate system

模型的相关参数设定如表1所示。

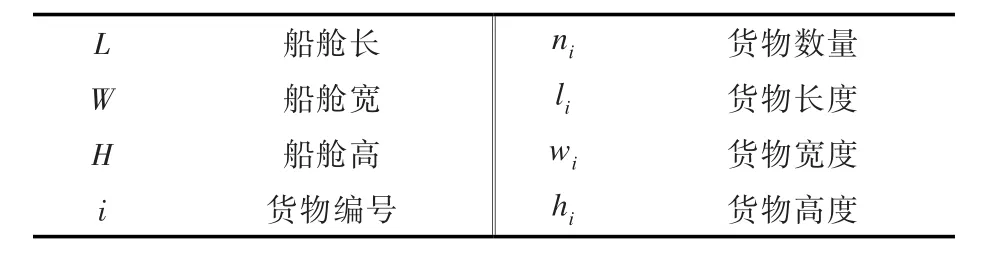
表1 模型主要参数Tab.1 The main parameters of model

模型的目标函数为

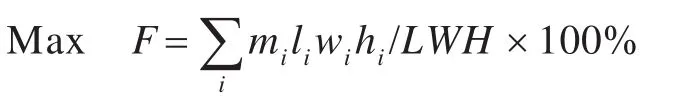
模型的约束条件为

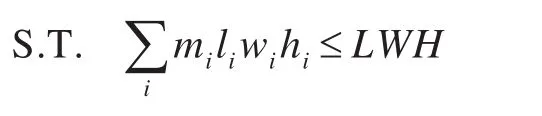
式中：F为船舱的空间利用率；mi为货物的装入数量。

2 模型求解及算法分析

2.1 启发式规则

2.1.1 定序规则

待装货物在装入船舱时，其装载的先后顺序直接影响装载结果。由于货物没有配装优先级约束，故待装货物的装载顺序主要参考对船舱空间利用率的影响。本文的装填思路是最大限度地填满空间，但随着空间分解的进行，空间会越来越狭小，而如果大尺寸货物的装载顺序靠后，极有可能造成大尺寸货物无法装载，最终降低船舱空间利用率的情况。故装填时应优先装入尺寸较大的货物，本文采用按待装货物最短边边长递减的顺序。

2.1.2 定位规则

图1已经确定了本文的坐标系，本文的定位规则采用占角策略，货物摆放在靠近原点的位置。

2.1.3 空间划分规则

本文对杂货船装载问题的优化主要体现在空间划分规则上。George和Robinson［2］最先提出了三空间划分原则，即将第1个货物放入当前空间左下角后，就形成了上方、右方、前方3个子空间（图2（a）），然后后面的货物就按照上空间、右空间和前空间的顺序进行装载。George和Robinson［2］还引入了“层”的概念，他们使用的是YZ-X层，每次装载都会产生3个子空间，按照Z-Y-X的遍历方式装载，直到所有剩余的货物不能装入任意一个剩余子空间，装载便结束。本文采用一种新的三空间划分方法，构建YZ-X层，在每一个YZ层内再构建Y-Z条，装载由角到条到层再到整个空间的顺序，空间划分方式按以下3种情况进行：

1）当前待装货物为层中的第1个装入货物，即Y-Z-X方式；

2）当前待装货物为条中第1个装入货物但不是层中的第1个装入货物，即X-Y-Z方式；

3）当前待装货物不是条中第1个装入货物，即X-Z-Y方式。

在一般问题中，所有情况均按如图2（b）所示的Y-Z-X方式分解空间，本文仅在第1种情况下采用此种划分方法。当装箱为第2种情况时，当前空间X方向的长度由层中第1个装入的货物决定，若X方向尺寸较小，在后续划分空间时，前空间会较狭窄，而过狭窄的前空间极易成为无法装入任一货物的废弃空间。当装箱为第3种情况时，当前空间X方向的长度由层中第1个装入的货物决定，当前空间Y方向的长度由条中第1个装入的货物决定，若X，Z方向尺寸较小，在后续划分空间时，前空间和上空间都会较窄，易成为废弃空间。针对这类情况，本文提出一种新的空间分配方式，即考虑将狭窄的空间提前视为废弃空间，分情况采用相应的空间划分规则，加大可用空间的体积，进而提高整体空间利用率。当处于第2种情况时，将空间划分为前方、右方和上方3个子空间（图2（c）），按照X-Y-Z的遍历方式装载；当为第3种情况时，将空间划分为前方、上方和右方3个子空间（图2（d）），按照X-Z-Y的遍历方式装载。

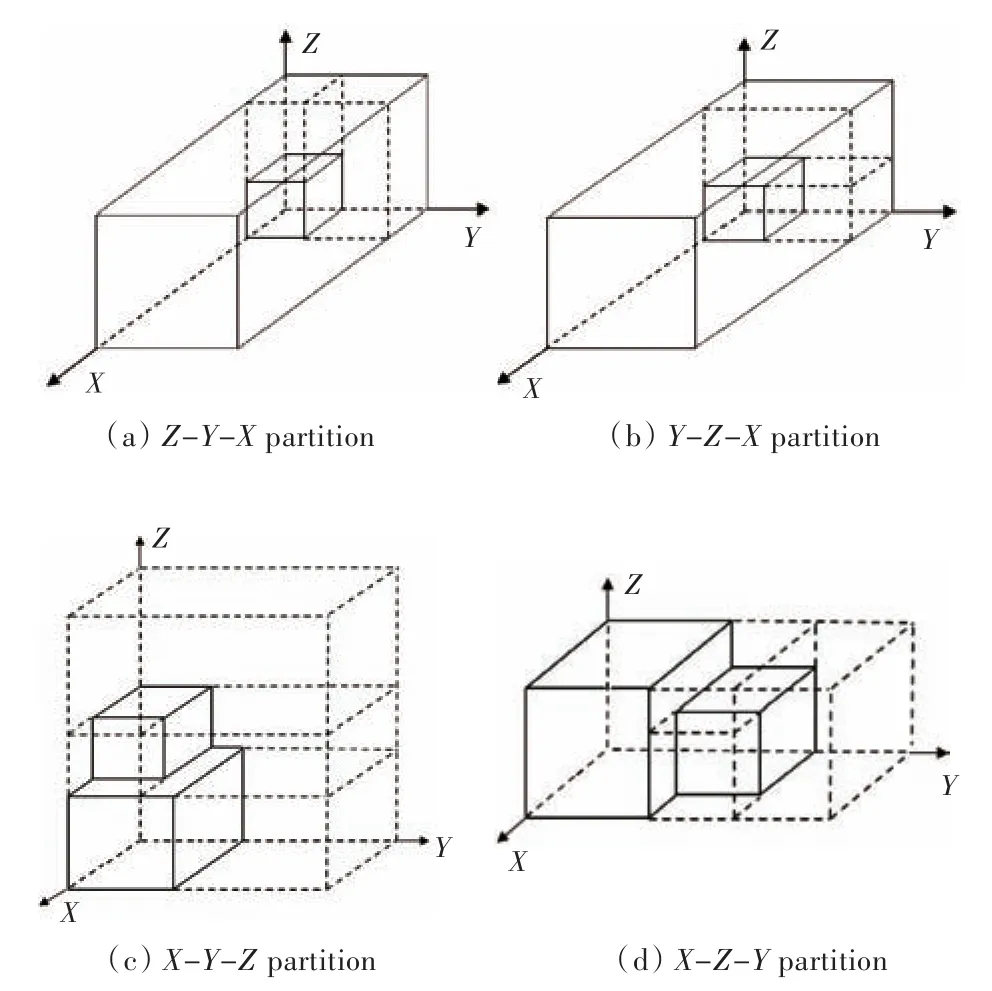
图2 空间划分方式Fig.2 Three-space partition method

2.1.4 空间合并规则

每次装载前，若存在废弃空间，则将当前装载空间与废弃空间合并，以使废弃空间再利用。空间合并有3个方向上的空间合并，分别为左右合并（图3（a））、上下合并（图3（b））和前后合并（图3（c））。空间合并的步骤如下：

1）装载前，当存在废弃空间时，对废弃空间进行搜索。

2）依次判断废弃空间与当前空间是否共XZ面、是否共XY面、是否共YZ面。

3）若共XZ面，则将该废弃空间与当前空间进行左右合并；若共XY面，则将该废弃空间与当前空间进行上下合并；若共YZ面，则将该废弃空间与当前空间进行前后合并。

4）将合并后的空间作为新的装载空间。

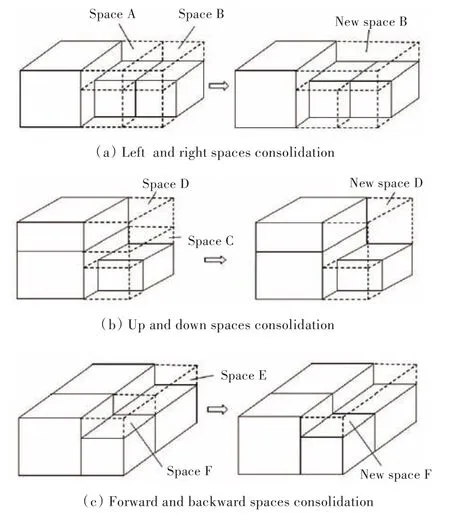
图3 空间合并方式Fig.3 Spaces consolidation method

2.2 遗传算法

所谓遗传算法，就是模拟生物进化优胜劣汰的过程搜索最优解。一个编码P即一个生物个体，对应杂货船装载问题中的一种装载方案。由多个个体组成一个生物种群，群体大小M对应于装载方案的数量。适应度代表了个体适应生存环境的能力，对应于装载问题中的船舱空间利用率，个体适应度越高，其编码代表的装载方案越优秀，其装载信息保留下来的概率越大。繁殖进化要经历选择、交叉和变异。选择装载方案中对船舱空间利用率较高的方案作为父代群体，在这些空间利用率较高的装载方案之间交换装载信息或调整部分自身装载信息，以此来产生空间利用率更高的装载方案，也就是子代群体，然后不断重复这种过程，以使得到的装载方案的空间利用率越来越高，最终获得空间利用率令人满意的装载方案。

2.2.1 编 码

待装货物的装载顺序已经由启发式定序规则确定，装载方式也由启发式定位规则和空间划分规则确定，目前，影响装载的决策变量仅剩下货物的放置状态，即货物的各个面与船舱各个面的位置关系（存在6种位置关系）。在编码中存储决策变量的信息，即货物的放置状态。待装货物有k种，编号为i=1，2，…，k，每种货物的数量为ni，编码表示为

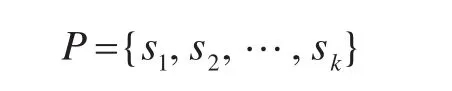
si为种类编号为i的货物的放置状态，取值范围为｛1，2，3，4，5，6｝。为尽可能减少废弃空间，同一种货物的放置状态需相同。种类编号为i的货物的原始放置状态为si=1，表示货物的长、宽、高与船舱的长、宽、高一一平行对应放置，即li∥L，wi∥W，hi∥H。由于货物的放置状态可以任意旋转，故形成了6种可影响总体空间的放置状态，如表2所示。

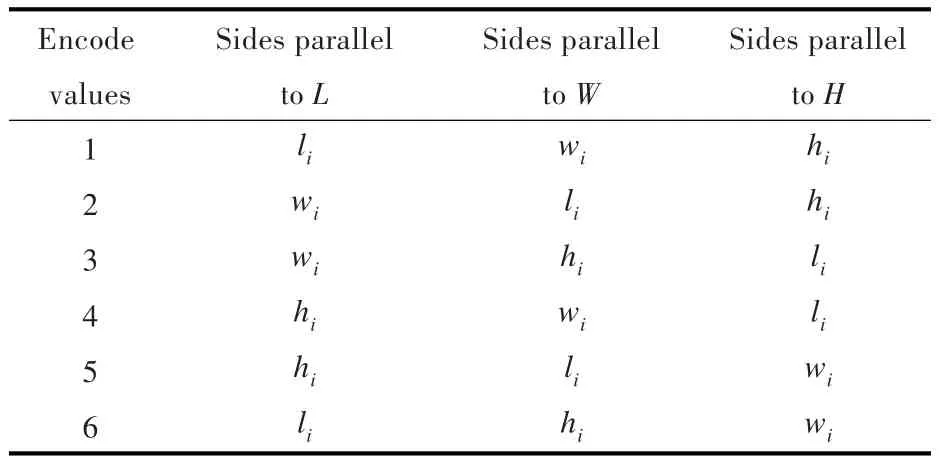
表2 编码值对应表Tab.2 Encoding values

2.2.2 解 码

由启发式定序规则确定货物的装填顺序，启发式定位规则和空间划分规则确定货物放置的位置，编码确定待装货物的放置状态，继而确定一种装载结果。解码是将编码转化成装载结果的过程。解码后，可以确定每种货物能装入船舱的数量和放置状态。设种类编号为i的货物能装入mi个，解码表示为

2.2.3 适应度函数

一般的遗传算法适应度函数由目标函数变化而成，本文的适应度函数也参考目标函数空间利用率，定义如下：

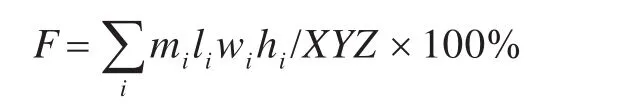
2.2.4 选择操作

本文是采用轮盘赌注法进行遗传算法中的选择操作［11］。已知群体大小为M，父代群体为轮盘赌注法的操作步骤如下：

1）计算出群体中每个个体的适应度总和。

2）计算出每个个体的相对适应度大小，即各个个体被选择为遗传父代的概率。第j个个体的选择概率

3）计算各个个体的累积概率

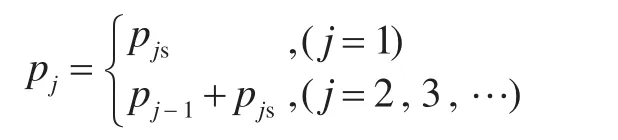
4）生成一个［0，1］随机数，判断随机数所在的取值区间，若随机数取值在之间，则Pj被选中，如图4所示。

图4 轮盘赌注法Fig.4 Roulette betting method

5）重复第4）步，得到M个个体组成的新群体

2.2.5 交叉操作

在装箱问题中，常用的交叉方法为部分映射交叉［12］，本文选用的编码方式不适用于部分映射交叉，故选用简单的两点交叉。交叉概率为Pc，准备进行交叉操作的群体为交叉步骤如下：

2）生成一个［0，1］随机数，若随机数大于Pc，则不交叉，若随机数小于Pc，则对行后续交叉操作。

3）在［1，k］之间生成2个随机整数a，b（a＜b）作为交叉点，交换位于ab之间的基因段，如图5所示。

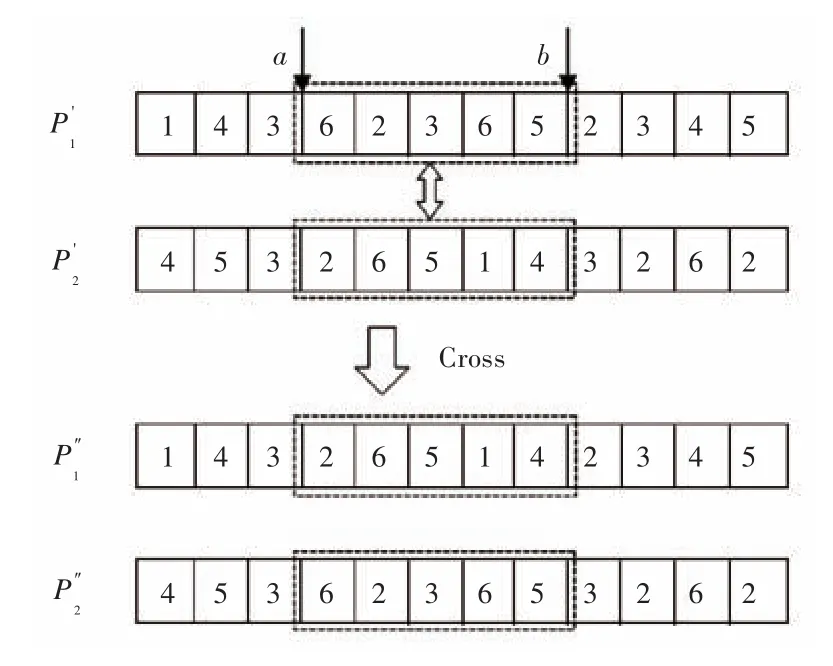
图5 简单两点交叉Fig.5 Simple two-point crossover

4）对剩余个体重复第2）步和第3）步，得到M个个体组成的新群体

2.2.6 变异操作

根据本文的编码方式，采用两点顺序逆转方式进行变异。变异概率为Pm，准备进行变异操作的群体为变异步骤如下：

2）生成一个［0，1］随机数，若随机数大于Pm，则不变异，若随机数小于Pm，则对进行后续的变异操作。

3）通过随机数生成函数在［1，k］之间的2个整数a，b（a＜b）作为变异点，逆转位于ab之间的基因段，如图6所示。

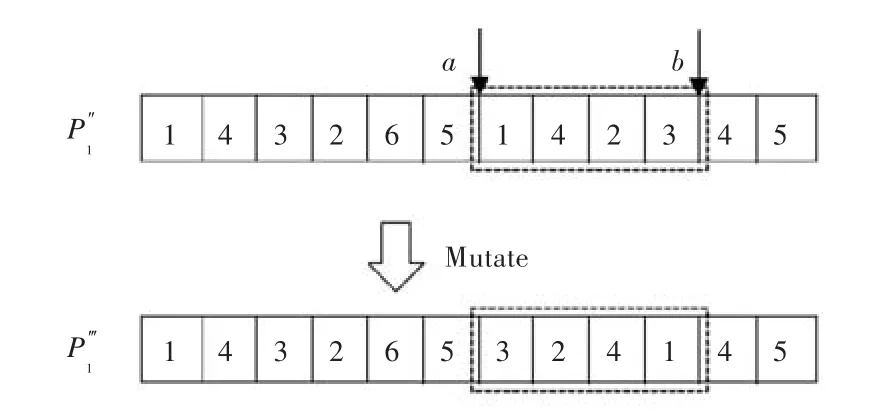
图6 顺序逆转变异Fig.6 Order reversal mutation

4）对剩余个体重复第2）步和第3）步，得到M个个体组成的新群体

2.2.7 最优保存策略

最优保存策略可以避免父代中的优秀个体在遗传迭代的过程中消失。最优保存的步骤为：

1）计算父代群体{P1，P2，P3，…，PM}中所有个体的适应度，找出父代中适应度最高的个体，即最优父代，其适应度为Fmax。

2.3 仿真程序设计

基于上文对启发式规则和遗传算法的描述，借助Matlab仿真软件进行算法实现，程序流程如图7所示。

3 算例分析

3.1 测试数据

Loh和Nee［3］研究的问题与本文十分相似，他们在研究中给出了多组经典的测试数据。之后，Bischoff和Ratcliff等［4-5］、Gehring和Bortfeldt［6］先后使用这组数据对自己的算法进行了测试。本文也采用该组数据进行了算法测试，测试数据如表3所示。

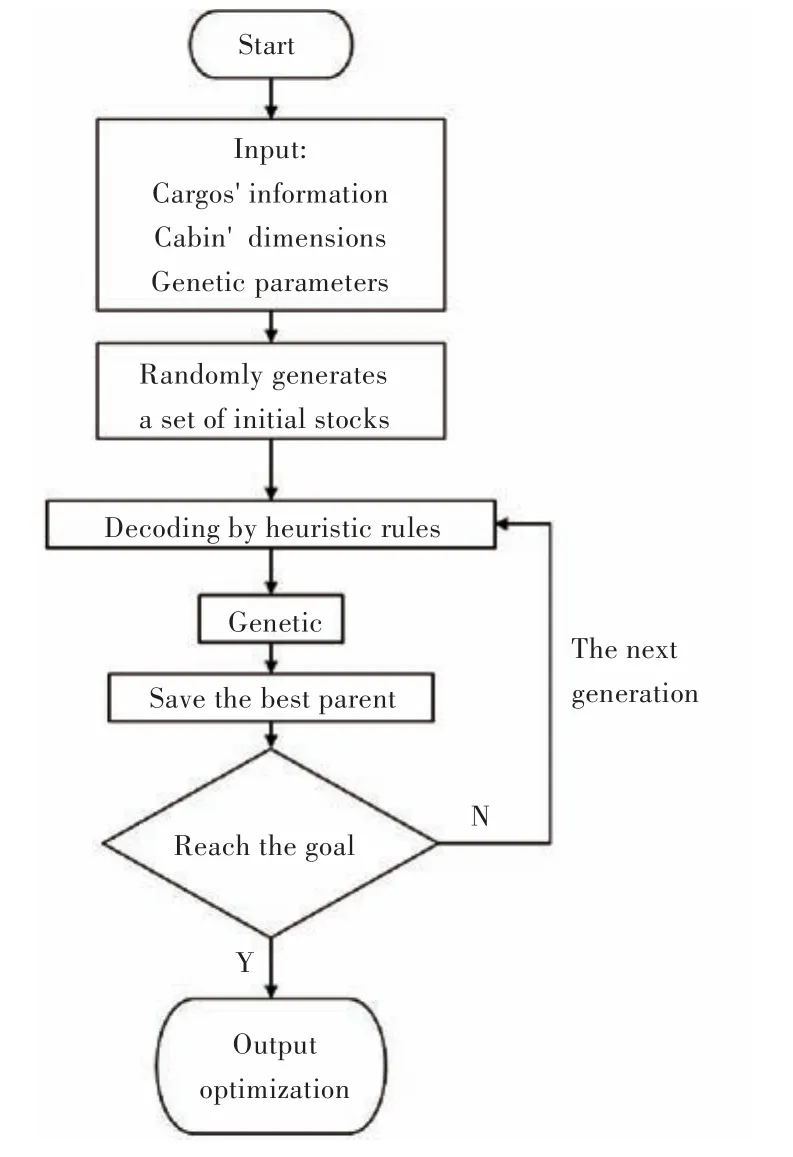
图7 程序流程图Fig.7 Program flow chart

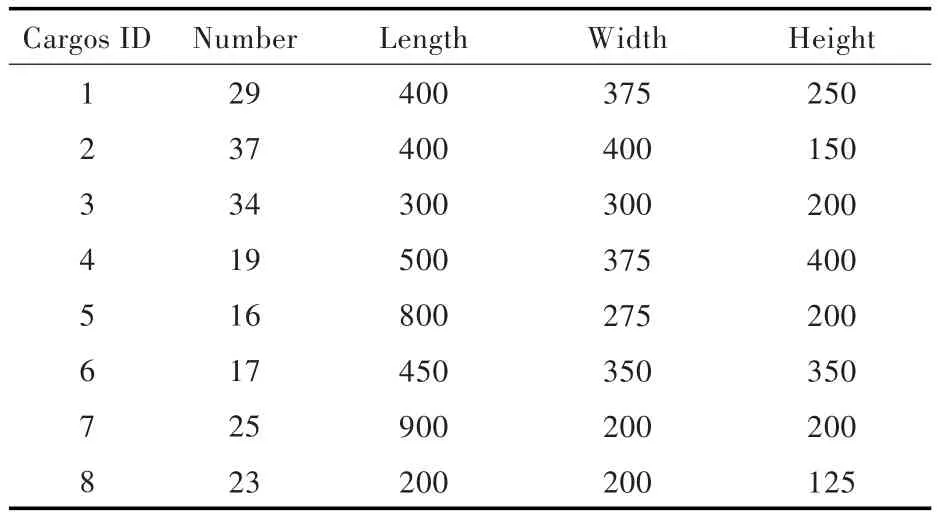
表3 测试数据Tab.3 Test data

3.2 测试结果

本文的各项参数取值分别为：

群体规模M60

遗传代数GEN0.95

交叉概率Pc0.01

变异概率Pm0.95

针对这组测试数据进行仿真试验，得到了16组试验结果，试验结果分布如图8所示。

试验结果表明，本文算法的空间利用率均分布在93%～88%之间，空间利用率可达92.94%，其具体的装载方案如表4所示。

3.3 对比分析

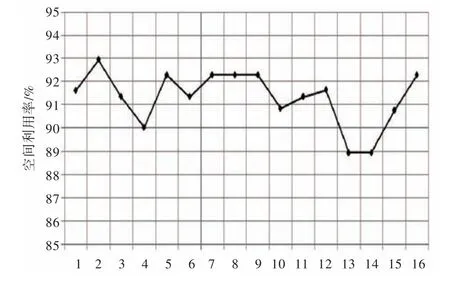
图8 仿真试验结果分布Fig.8 Distribution of simulation results

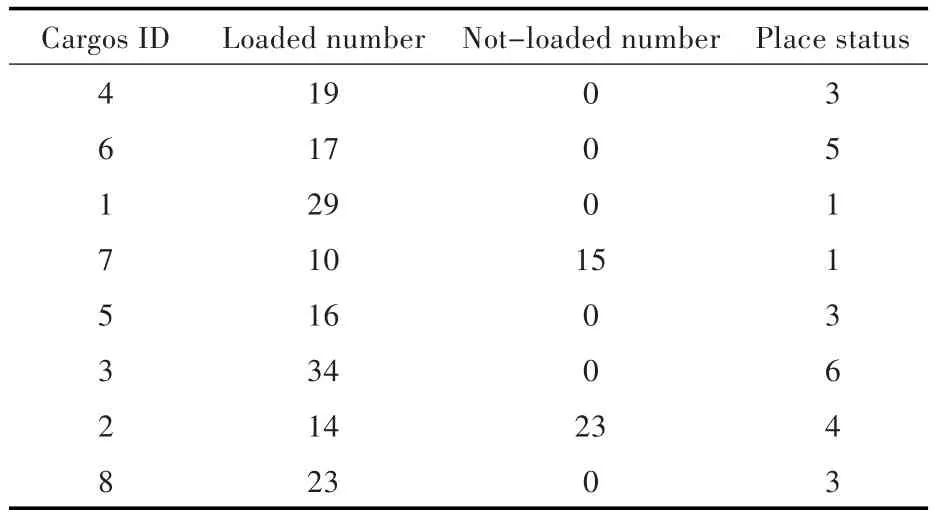
表4 测试结果Fi=92.94%Tab.4 Test results Fi=92.94%

对同一组测试数据，Bischoff等［4］算法的空间利用率为89.7%，Bischoff和Ratcliff［5］算法的空间利用率为90.3%，Gehring和Bortfeldt［6］算法的空间利用率为89.8%，而本文算法的空间利用率可达92.94%。通过与这些算法试验结果的比较，发现在解决同类问题时，本文的算法具有显著的优势。

4 结 语

本文分析了一般杂货船装载问题的配载特点，构建了杂货船装载问题的一般模型，并提出了一种新的空间划分方式下的混合遗传算法，用以弥补以往启发式算法对闲置空间再利用的不足。借助Matlab仿真软件，对文献［3］的经典测试数据进行了仿真试验，仿真结果达92.94%，验证了本文算法对杂货船装载问题优化结果的有效性。

［1］ 徐丽丽.集装箱单箱三维装载优化研究［D］.济南：山东大学，2008.

［2］ GEORGE J A，ROBINSON D F.A heuristic for pack⁃ing boxes into a container［J］.Computers&Operations Research，1980，7（3）：147-156.

［3］ LOH T H，NEE A Y C.A packing algorithm for hexahe⁃dral boxes［C］//Conference of Industrial Automation. Singapore，1992.

［4］ BISCHOFF E E，JANETZ F，RATCLIFF M S W.Load⁃ing pallets with non-identical items［J］.European Jour⁃nal of Operational Research，1995，84（3）：681-692.

［5］ BISCHOFF E E，RATCLIFF M S W.Issues in the de⁃velopment of approaches to container loading［J］.Ome⁃ga，1995，23（4）：377-390.

［6］ GEHRING H，BORTFELDT A.A genetic algorithm for solving the container loading problem［J］.International Transactions in Operational Research，1997，4（5/6）：401-418.

［7］ 何大勇，查建中，姜义东.遗传算法求解复杂集装箱装载问题方法研究［J］.软件学报，2001，12（9）：1380-1385. HE Dayong，ZHA Jianzhong，JIANG Yidong.Research on solution tocomplexcontainer-loadingproblem based on genetic algorithm［J］.Journal of Software，2001，12（9）：1380-1385.

［8］ 翟钰，孙小明.多种物品三维装箱问题的一种启发式算法［J］.上海交通大学学报，2007，41（8）：1244-1247. ZHAI Yu，SUN Xiaoming.A heuristic algorithm for three-dimensionalcontainerloading problem with non-identical items［J］.Journal of Shanghai Jiaotong University，2007，41（8）：1244-1247.

［9］ 陈德良，陈治亚.三维装箱问题的智能启发式算法［J］.中南林业科技大学学报，2009，29（3）：134-137. CHEN Deliang，CHEN Zhiya.An intelligent heuristic approach to three-dimensional bin-packing problem［J］.Journal of Central South University of Forestry& Technology，2009，29（3）：134-137.

［10］ 徐宁，李春光，张健，等.几种现代优化算法的比较研究［J］.系统工程与电子技术，2002，24（12）：100-103. XU Ning，LI Chunguang，ZHANG Jian，et al.Studies on some modern optimization algorithms［J］.Systems Engineering and Electronics，2002，24（12）：100-103.

［11］ 张琛，詹志辉.遗传算法选择策略比较［J］.计算机工程与设计，2009，30（23）：5471-5474. ZHANG Chen，ZHAN Zhihui.Comparisons of selec⁃tion strategy in genetic algorithm［J］.Computer Engi⁃neering and Design，2009，30（23）：5471-5474.

［12］ 李书全，孙雪，孙德辉，等.遗传算法中的交叉算子的述评［J］.计算机工程与应用，2012，48（1）：36-39. LI Shuquan，SUN Xue，SUN Dehui，et al.Summary of crossover operator of genetic algorithm［J］.Computer Engineering and Applications，2012，48（1）：36-39.

［责任编辑：卢圣芳］

General cargo ship loading problems based on the hybrid genetic algorithm

ZHU Ying1，XIANG Xianbo1，YANG Yuntao2

1 School of Naval Architecture and Ocean Engineering，Huazhong University of Science and Technology，Wuhan 430074，China

2 Systems Engineering Research Institute，Beijing 100094，China

General cargo ship loading problems belong to general three-dimensional container loading problems.In this paper,based on the analysis of general cargo ship loading problems and taking the goal of maximizing the space utilization,a mathematical model of general cargo ship loading problems is estab⁃lished.By analyzing the characteristics of the model,a hybrid genetic algorithm combined with the heuris⁃tic algorithm and the genetic algorithm is presented,and a new type of three-space partition method is de⁃signed,both of which being realized along with simulation and experimental confirmation.By examining a classic set of test data of Loh&Nee as an example,the space utilization is seen to reach 92.94%,which demonstrates distinct advantages to similar algorithms for the container loading problems.The experimental results show that the hybrid genetic algorithm is feasible on solving general cargo ship loading problems.

general cargo ship；three-dimensional container loading；heuristic algorithm；genetic algorithm

U695.2+5

A

10.3969/j.issn.1673-3185.2015.06.019

http://www.cnki.net/kcms/detail/42.1755.TJ.20151110.1026.036.html期刊网址：www.ship-research.com

朱莹，向先波，杨运桃.基于混合遗传算法的杂货船装载优化问题［J］.中国舰船研究，2015，10（6）：126-132. ZHU Ying，XIANG Xianbo，YANG Yuntao.General cargo ship loading problems based on the hybrid genetic algorithm［J］.Chinese Journal of Ship Research，2015，10（6）：126-132.

2015-05-28 < class="emphasis_bold"> 网络出版时间：

时间：2015-11-10 10:26

湖北省自然科学基金资助项目（2014CFB253）；高等学校博士学科点专项科研基金资助项目（20120142120045）；中央高校基本科研业务费专项基金资助项目（2015TS006）

朱莹，女，1991年生，硕士生。研究方向：舰船系统工程。E-mail：zhuying@hust.edu.cn向先波（通信作者），男，1978年生，博士，副教授。研究方向：航行器/机器人智能控制，舰船系统优化。E-mail：xbxiang@hust.edu.cn