典型船舶板架拓扑与形状优化设计

张会新，杨德庆

1上海交通大学船舶海洋与建筑工程学院，上海200240

2上海交通大学海洋工程国家重点实验室，上海200240

典型船舶板架拓扑与形状优化设计

张会新1，2，杨德庆1，2

1上海交通大学船舶海洋与建筑工程学院，上海200240

2上海交通大学海洋工程国家重点实验室，上海200240

以典型板架结构（船底板架和上层建筑板架）为研究对象，探讨结构拓扑与形状优化设计方法在船舶设计中的应用。对船底板架结构进行形状和尺寸优化（优化目标是指定应力约束条件下结构重量最小），优化后的结构重量减少了15.82%。为改善舱室顶部空间布局，提高舱室顶部板架结构的固有频率，对上层建筑板架进行拓扑优化，寻求材料最优分布，并在对其进行静力分析和模态分析的基础上，以体积百分比为约束条件，以板架固有频率为目标函数，得到拓扑优化后的结构型式，新结构型式使材料分布更加合理，有利于舱室顶部管道和电缆等的铺设。研究表明，在目前的板架结构设计中，可广泛应用结构拓扑与形状优化设计技术。

板架结构；结构优化；拓扑优化；固体各向同性惩罚微结构模型

0 引 言

结构优化设计运用于船舶领域始于20世纪60年代，Moe等发表了关于汽车运输船甲板优化的论文，首次把数学规划论应用到了船舶结构领域，标志着船舶结构设计思想的重大飞跃。经过多年研究，针对局部结构（如舱口形状、剖面结构等）的尺寸优化和形状优化已相当成功，而结构拓扑优化进展则相对缓慢。拓扑优化［1］是以材料分布为优化对象，在设计空间中找到最佳的材料分布方案。目前，连续体拓扑优化理论已较为成熟，在汽车工业、航天工程等领域有着较广泛的应用［2-5］，在船舶行业亦有所应用［6-7］。但有关实用化的船舶构件拓扑与形状优化设计的案例还较少。本文将以板架结构为研究对象，分别选取船底板架和上层建筑板架结构，探索结构形状、拓扑和尺寸优化设计方法在实际船舶工程设计中的可行性与实用性，包括板架最佳拓扑型式（开孔状况）、构件最佳形状（如肘板）和最佳尺寸（如扶强材）等，给出基于实际工程设计的优化模型和设计变量形式。

1 船体板架结构力学分析模型

以船底板架为例，待优化板架模型主要由外板、纵骨和横舱壁组成。设船长方向为X轴，正方向由船艉指向船艏；船宽方向为Y轴，正方向由右舷指向左舷；型深方向为Z轴，正方向由船底指向顶部甲板。模型沿船长方向选取3个舱段，沿船宽方向选取5个纵骨间距宽，设舱室跨距为4.5 m，纵骨间距 0.75 m，外板厚 17 mm，横舱壁厚12.5 mm，纵骨腹板厚 12.5 mm，纵骨面板厚36 mm，大肘板厚10 mm，小肘板厚10 mm，扶强材厚10 mm，如图1～图2所示。

板架结构材料为普通钢（上层建筑板架）/高强度钢（船底板架），其密度为7 850 kg/m3，弹性模量为210 GPa，泊松比为0.3。

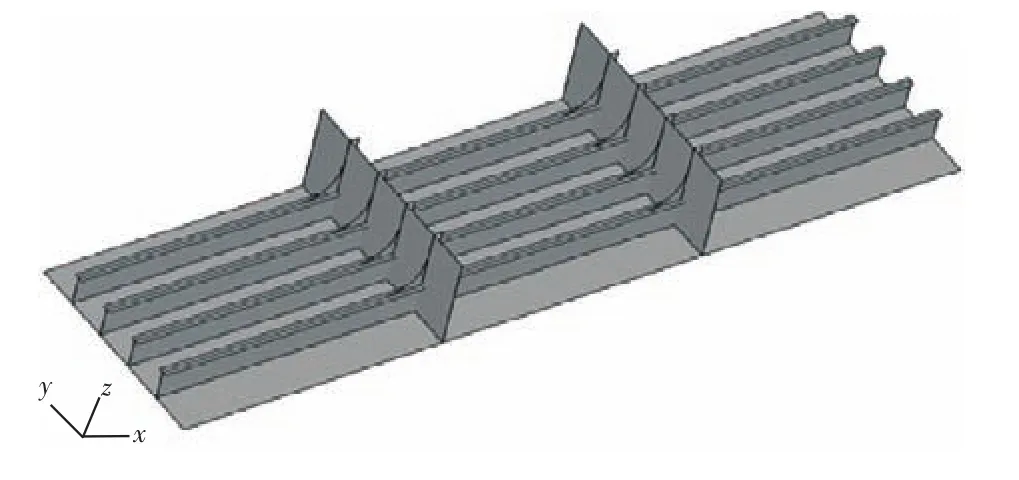
图1 板架结构三维模型Fig.1 Three-dimensional model of grillage structure

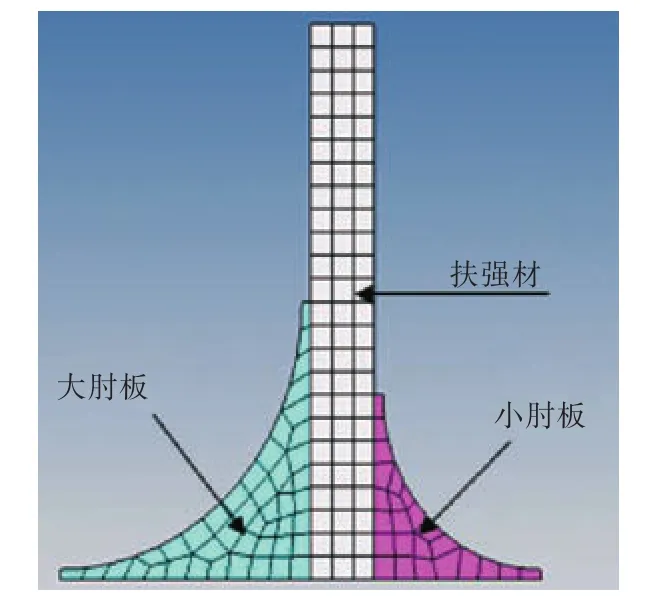
图2 端部连接Fig.2 Connection of the ends

2 重量目标下船体板架尺寸和形状优化

一般工程优化设计寻求在满足应力约束的条件下结构重量最小。位移和载荷边界条件如下。

1）边界条件：船底板四边刚性固定约束，放松最右端边界支承的X向自由度；两道横舱壁边界除X向自由度外全部约束。首、尾两端纵骨边界与船底板相对应，一端刚性固定，一端除X向自由度外全部约束。

2）载荷工况：板架结构所承受的载荷包括沿船长方向的总纵弯曲应力和作用于船底板的水柱压力。总纵弯曲应力取100 MPa，在实际模型加载中将其转化为节点力作用于模型两端，沿X方向。水柱压力实取20 000 mmH2O压力，垂直作用于船底板。

首先，进行板架尺寸与形状优化，设计变量分为尺寸变量和形状变量，总数14个。其中形状变量包括纵骨、肘板和扶强材的几何形状变量，尺寸变量包括纵骨的腹板和面板厚度，以及大、小肘板厚度和扶强材厚度。尺寸设计变量中，大肘板厚度t1与小肘板厚度t2及扶强材厚度t5进行变量连接，以保证三者厚度优化后为同一数值。具体变量涉及的构件如图3所示。

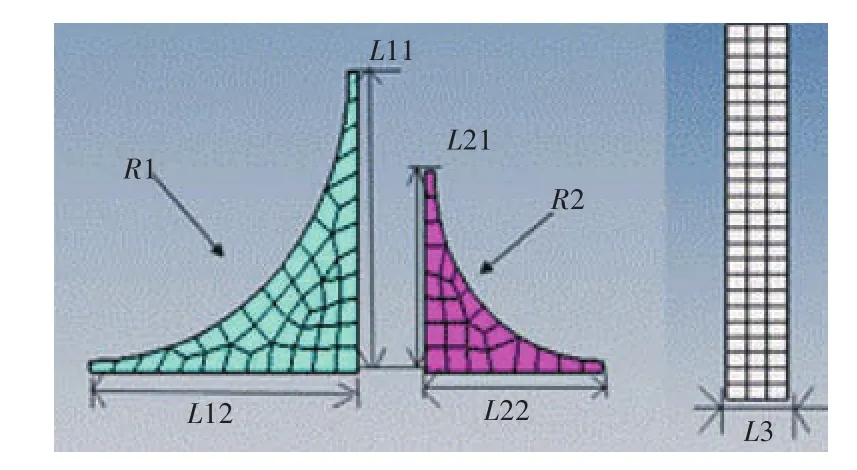
图3 主要设计变量Fig.3 The main design variables

应力和尺寸的上、下限约束条件为：

1）应力（屈服强度）约束，保证结构应力不大于355 MPa。

2）纵骨的几何形状约束，保证面板宽度与腹板高度的比值不小于0.25。

3）肘板的几何形状约束，保证优化后其几何形状符合生产和施工工艺的要求。

4）最小板厚要求。

以整个船体板架结构重量最小为目标函数，采用商用结构优化软件HyperWorks/OptiStruct进行优化求解。

式中：Hs为n维板厚度设计变量向量；Xs为m维形状设计变量向量；yis与si(Xs)分别为待设计板的材料密度与面积为板单元应力与分别为板单元应力约束的上、下限；与分别为评价点p处的位移和约束上限；k为工况编号；XU，XL分别为形状变量的上、下限；分别为厚度设计变量的上、下限约束。

本文中设计变量的上、下限如表1所示。

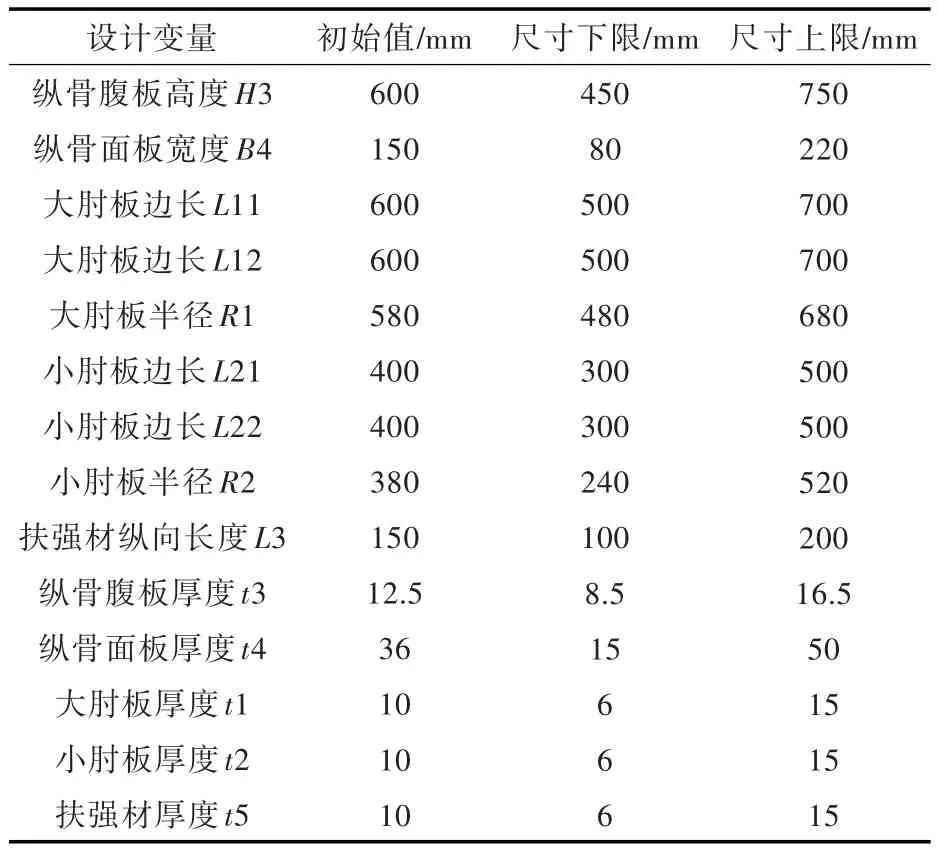
表1 设计变量初始值及上、下限Tab.1 The upper，lower limits and initial values of the design variables

屈服强度约束：通过设定单元vonMises应力上限值为355 MPa，保证单元所受的合成应力值不大于355 MPa。船底板边界的一排单元不考虑应力约束。纵骨的几何形状约束：对于纵骨腹板高度H3和纵骨面板宽B4，需保证B4/H3≥0.25。肘板的几何形状约束：为了符合生产和施工工艺的要求，肘板圆弧边半径和肘板直角边长应满足一定的关系，在OptiStruct中，是建立不等式，通过约束其上、下限来实现工程实际中的几何形状约束。最小厚度约束为6 mm。表2所示为形状与尺寸优化设计结果。

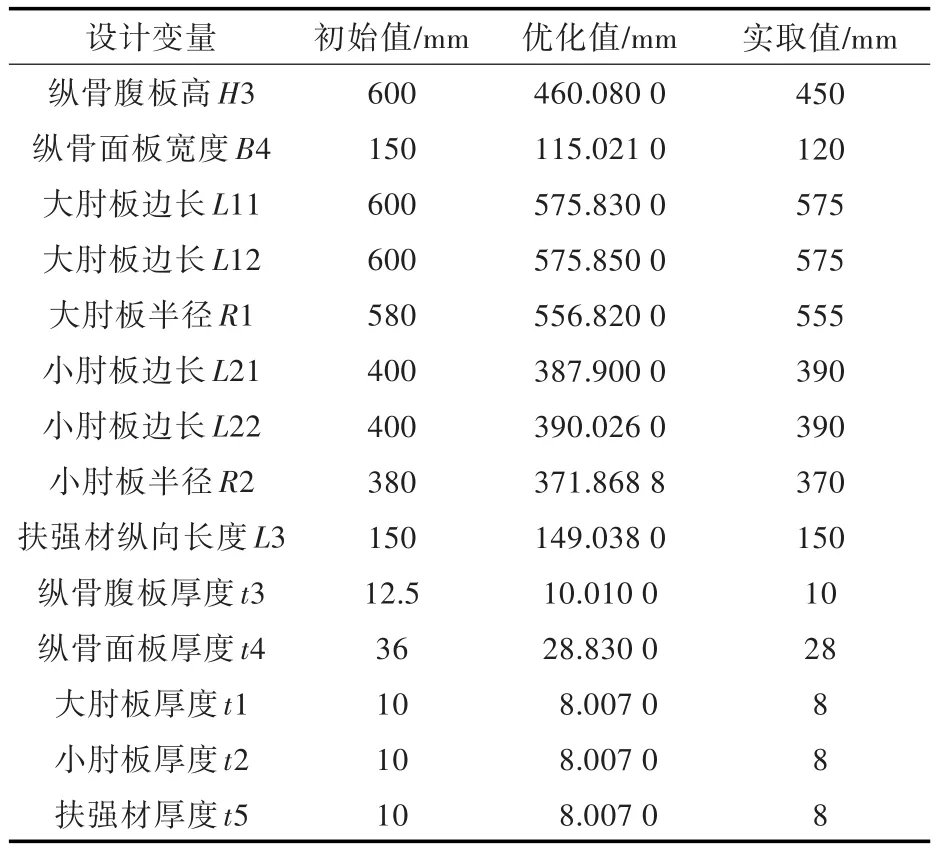
表2 形状与尺寸优化设计结果Tab.2 The shape and size optimization results

规范取整后，进行约束条件检查：经计算，单元最大应力值为354.4 MPa，B4/H3=2.667，肘板几何形状满足工艺要求，实取板厚大于6 mm，因而为可行方案。结构的初始设计重量为13.839 4 t，优化后的结构重量为11.65 t，与原板架结构相比，重量减少了15.82%，减少数值为2.18 t。

3 结构拓扑优化的变密度法理论

在拓扑优化中，常用的方法有均匀化方法和变密度法。本文采用变密度方法，此方法由均匀化方法发展而来，其基本思想是引入一种假想的密度可变材料，建立物理参数（例如，弹性模量、泊松比、许用应力等）与材料密度之间的关系。在对结构进行有限元划分之后，每个独立单元的“单元密度”是相同的，然后将有限元模型设计空间每个单元的“单元密度”作为设计变量。该“单元密度”同结构的材料参数有关（单元密度与材料弹性模量之间具有某种假设的函数关系），在0～1之间连续取值，优化求解后，设计空间的单元密度为0～1之间的某个值。对于单元密度为0的区域，表示该处单元为空，此处材料可以删除；对于单元密度为1的区域，表示该处单元很重要，需要保留；当单元密度处于中间值时，该中间值代表了这个单元的假想材料的密度值。变密度法中，常见的插值模型包括固体各向同性惩罚微结构模型（Solid Isotropic Microstructures with Penalization，SIMP）和材料属性的有理近似模型（Rational Approximation of Material Properties，RAMP）等。

SIMP或RAMP是通过引入惩罚因子对中间密度值进行惩罚，以使中间密度值向0～1的两端聚集，从而使连续变量的拓扑优化模型能够很好地逼近0～1离散变量的优化模型。中间密度单元对应一个很小的弹性模量，对结构刚度矩阵的影响变得很小。

SIMP材料插值数学模型为：

式中：a＞1，为惩罚因子；E0为实际材料的杨氏模量；ρ为单元密度。这样，就可以使具有中间密度的单元能替换成致密性材料或者是被剔除。则结构拓扑优化的一般数学模型可表示为

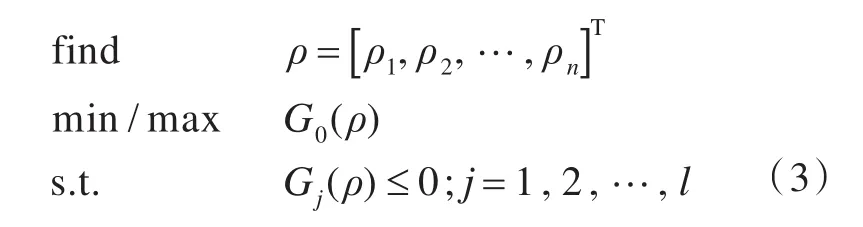
式中：n为设计变量个数；G0(ρ)为目标函数；Gj(ρ)为约束条件；l为约束方程的个数。

4 上层建筑板架拓扑优化设计

大型船舶（如散货船、集装箱船、大型游船等）舱室天花板以上区域往往是结构件与风管、电缆等共用的位置，因此有效利用舱室顶部空间就显得很重要，对上层建筑板架结构进行拓扑优化是有效利用设计空间的重要途径。本文待研究的上层建筑板架位移和载荷边界条件如下：

1）在约束方面，板架四边与船舶舱壁相连，并对其四边的6个自由度全约束；横舱壁类似，也约束其6个自由度。

2）在载荷方面，该板架主要承受沿船长方向的总纵弯曲应力，以及作用在甲板上的分布质量，如堆积于甲板上的货物和设备等。其中，板架结构承受的总纵弯曲应力为110 MPa，等效为节点力作用于甲板的两端；甲板上布置的设备以及堆积货物的载荷等效为分布质量，分布质量的变化范围为60～100 kg/m2。本例设为60 kg/m2，分布载荷与甲板自重的合成通过改变相应的甲板材料密度来实现，见下式：

式中：y1为合并处理后假想甲板材料相当面密度；y为原甲板材料的面密度；y*为甲板上分布质量的等效面密度；S为承载甲板的面积。

对板架结构进行静力分析计算，发现整个结构大部分区域的合成应力值小于180 MPa，可见结构减重潜力很大，可在提高其固有频率的情况下寻求更优的空间材料分布。

利用HyperWorks软件对上层建筑板架结构进行模态分析，得到其前10阶固有频率（表3）和对应的前6阶振型图［8］（图4）。

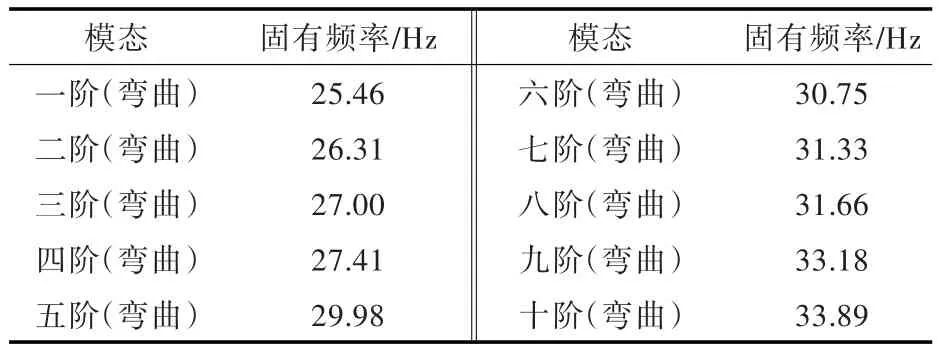
表3 结构前10阶模态分析Tab.3 10 modes of modal analysis

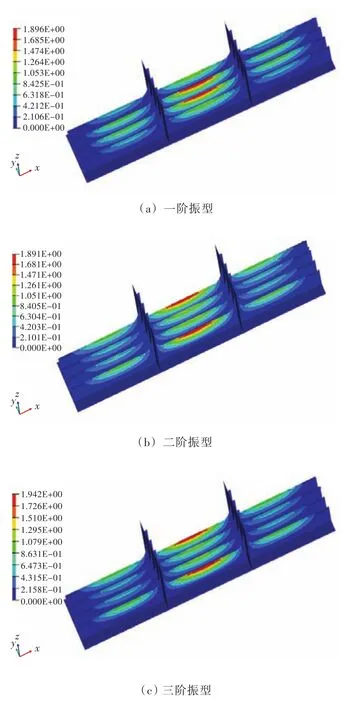
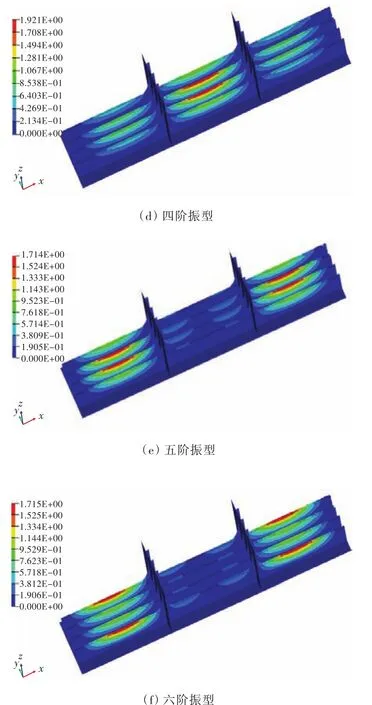
图4 振型图Fig.4 Mode shapes of vibration

由振型图可以看出，一阶振型位于板架中部区域内部的2根纵骨，二阶和三阶振型位于板架中部区域的2根边侧纵骨，四阶振型返回到中部区域内部的2根纵骨，从五阶振型开始，往前、后两端迁移。

结合板架模型前几阶固有频率值、振型和提高结构的固有频率设计目标，拓扑优化的目标函数设定为一阶与二阶固有频率之和，以使前2阶固有频率之和最大化。

拓扑设计区域为上层建筑板架结构中的纵骨，非设计区域为甲板、横舱壁和加强肘板等。优化设计参数设置如下：

1）设计变量：取设计区域的单元密度。

2）约束条件：从减轻结构重量的角度出发，对设计区域保留材料的体积百分比进行约束，设置体积百分比上限。

在基于SIMP材料插值模型的变密度法中，以板架结构模型的一阶与二阶固有频率之和最大化为目标，设定材料体积百分比约束，则结构拓扑优化数学模型表示为：

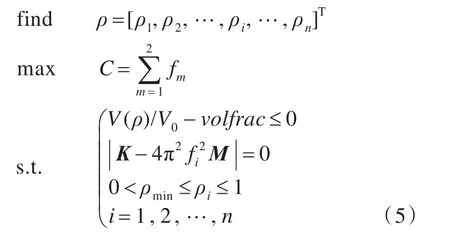
式中：C为固有频率之和；fi为第i阶固有频率；K，M分别为总刚度矩阵和总质量矩阵；V0和V分别为初始结构体积和最优结构体积；volfrac为体积百分比；ρmin为拓扑变量下限，用于避免有限元分析奇异性，通常取拓扑变量下限值ρmin=10-3。

采用OptiStruct软件进行优化。作为对比，将体积百分比约束条件设置为6组，体积百分比上限分别取15%，20%，25%，30%，35%和40%，并分别提交优化。图5所示为拓扑优化后的单元密度分布云图（由于各纵骨材料分布的近似性，故只观察中间跨距的单根纵骨）。图中，红色区域（单元密度为1）表示材料需保留，蓝色区域（单元密度为0）表示材料可以去除。各体积分数上限对应的目标函数值如表4所示。

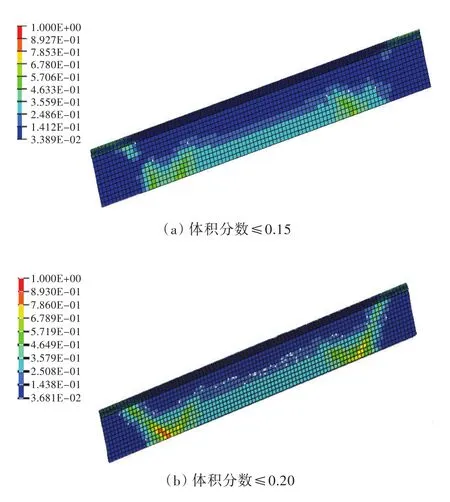
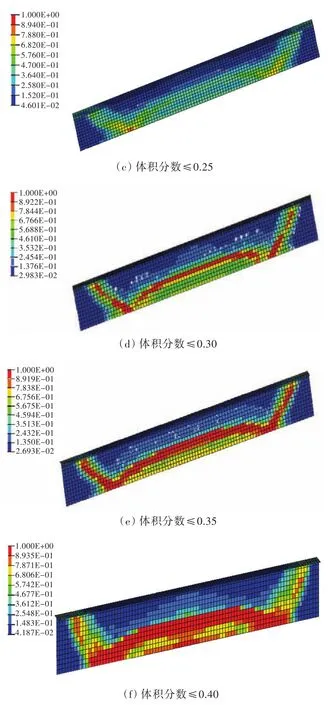
图5 不同体积分数约束下单元密度云图Fig.5 Element density contours of different volume fraction

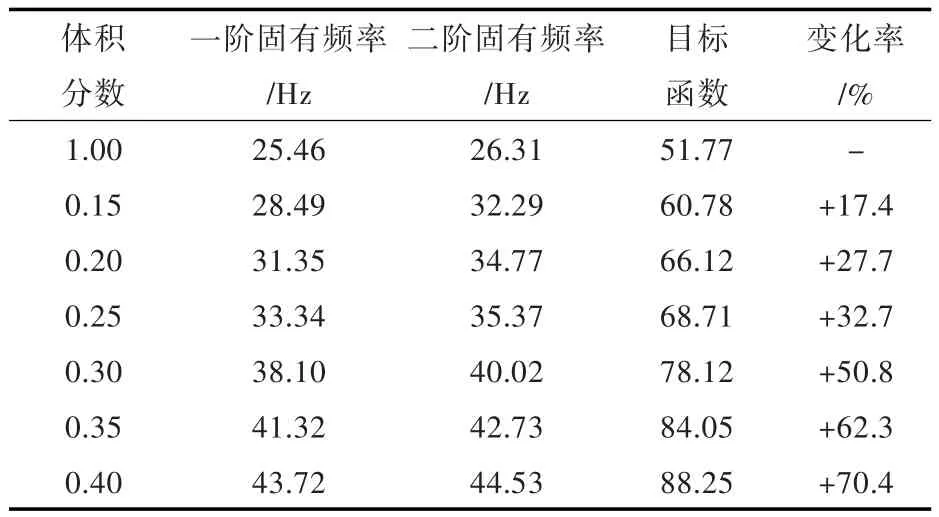
表4 各体积分数约束下对应频率和目标函数值Tab.4 Frequency and objective function in different volume fraction constraints

拓扑优化后，设计区域的单元密度值应尽量向0～1的两端靠拢，这样，拓扑结构会更清晰；同时，希望在提高原结构固有频率的基础上减轻结构重量，从而获取材料分布较优的方案，以在兼顾二者的基础上有一个合理的空间材料分布，确保管道、电缆和舱室顶部装饰物能有一个合理的布局，实现顶部空间的高效利用。从不同体积分数上限对应的优化后材料分布图来看（图5），体积分数上限为0.15和0.20的拓扑结构单元密度主要为蓝色区域；体积分数上限为0.25，0.30，0.35和0.40的拓扑结构单元密度分布更为理想。

对0.25，0.30，0.35和0.40的拓扑结构单元密度取不同的阈值（即只保留单元密度大于该阈值的单元），结果如图6～图9所示。

通过对比以上概念设计阶段的拓扑优化结果组图，综合考虑固有频率、结构重量和空间高效利用等指标，进行重新设计，得到纵骨腹板新的结构拓扑形式如图10所示。

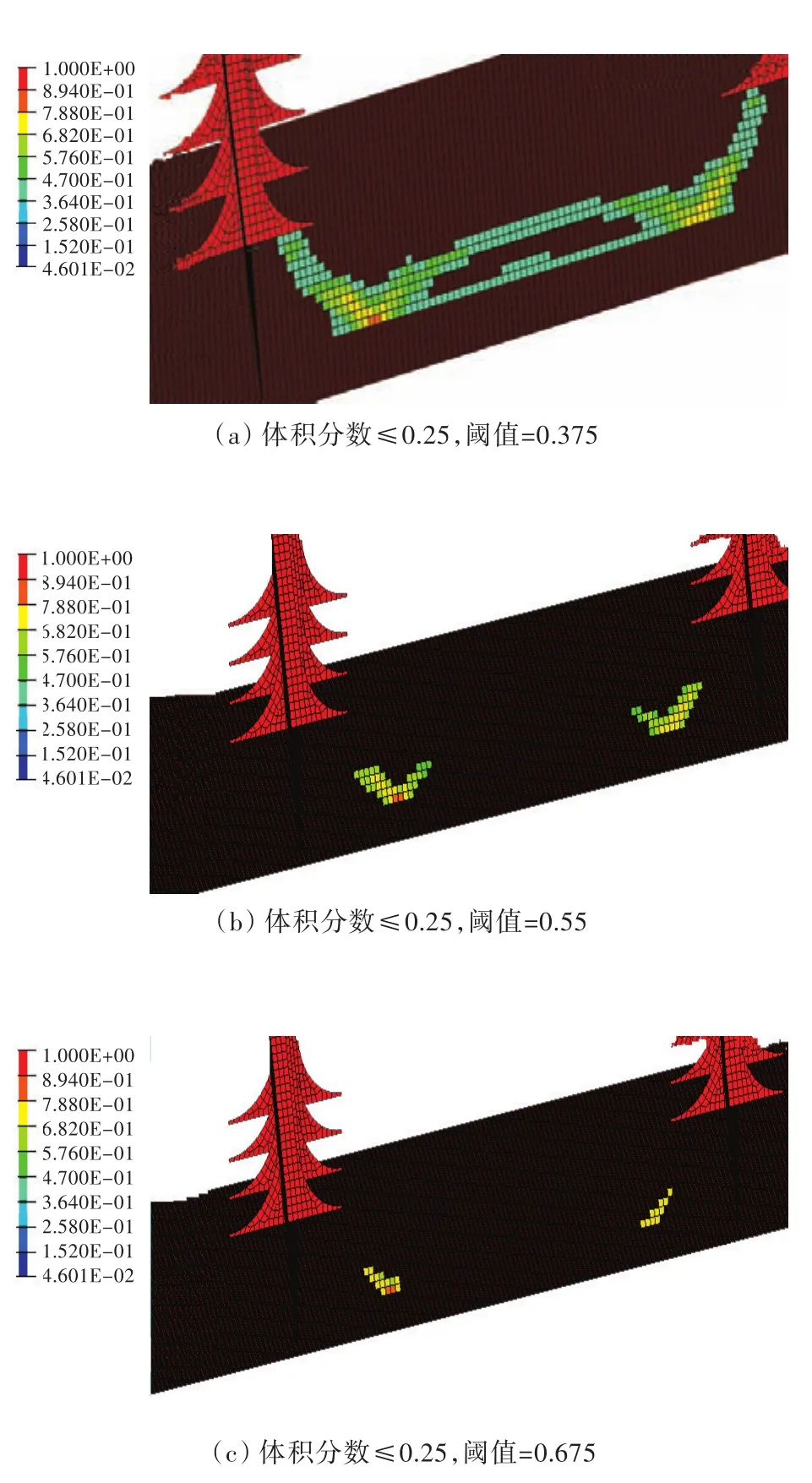
图6 体积分数≤0.25，阈值为0.375，0.55，0.675时的材料分布Fig.6 The material distribution when volume fraction≤0.25（upper bound is 0.375，0.55，0.675）

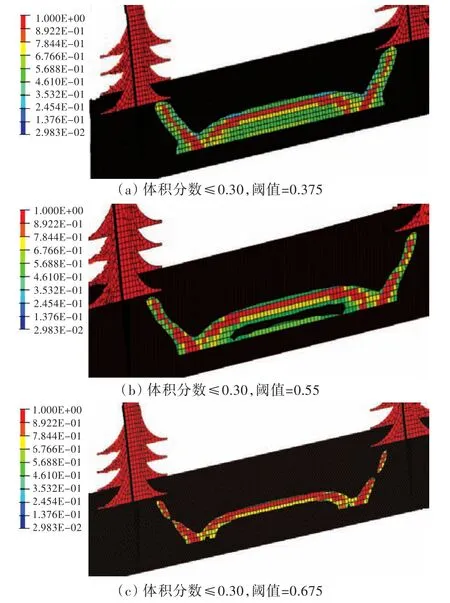
图7 体积分数≤0.30，阈值为0.375，0.55，0.675时的材料分布Fig.7 The material distribution when volume fraction≤0.3（upper bound is 0.375,0.55,0.675）

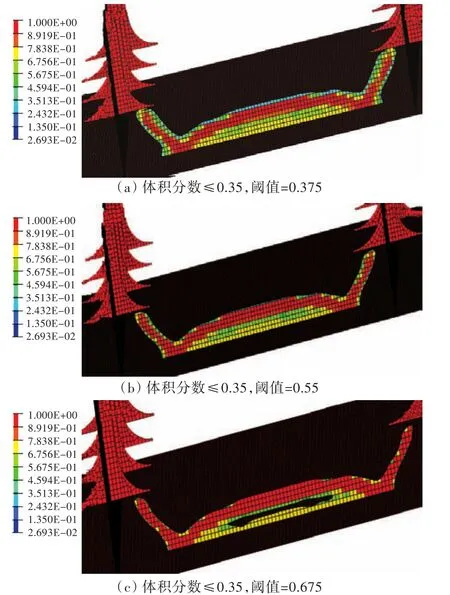
图8 体积分数≤0.35，阈值为0.375，0.55，0.675时的材料分布Fig.8 The material distribution when volume fraction≤0.35 (upper bound is 0.375,0.55,0.675)

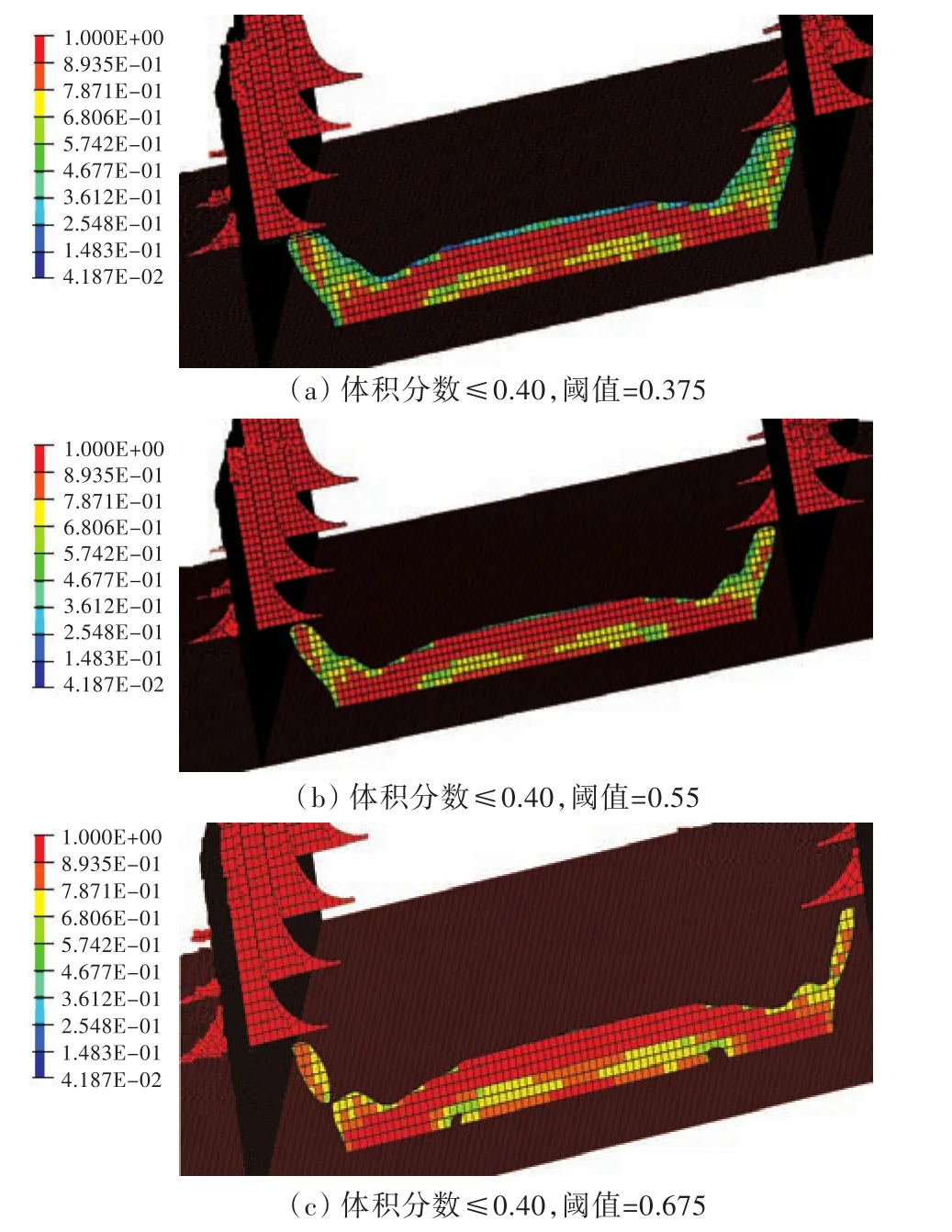
图9 体积分数≤0.40，阈值为0.375，0.55，0.675时的材料分布Fig.9 The material distribution when volume fraction≤0.4 (upper bound is 0.375,0.55,0.675)

图10 改进后的结构型式Fig.10 The new structure type

新的结构拓扑型式移除了多余的材料，合理地利用了结构材料，达到了轻量化设计的目的，同时，固有频率也有所提高。这种高腹板梁的掏洞设计也为船舶舱室各类管道、电缆的铺设提供了空间，提高了空间利用率。

5 结语

本文对船舶板架结构进行了拓扑与形状优化，以寻求材料最优分布。研究表明：通过对船底板架结构应用形状和尺寸的优化，在最小化重量目标下得到了新的结构型式，优化后的板架结构重量下降了15.82%。以拓扑优化变密度法建立的上层建筑板架结构优化模型，优化后的结构反映了其主传力路径，材料分布更为合理，结构重量减轻较显著，提高了结构固有频率，为管路、电缆的铺设提供了有效空间。本文的研究可为类似结构件的设计提供方法借鉴。

［1］ BENDSOE M P，SIGMUND O.Topology optimization：theory，methods and applications［M］.Berlin：Spring⁃er，2003.

［2］ ESCHENAUER H A，OLHOFF N.Topology optimiza⁃tion of continuum structures：a review［J］.Applied Me⁃chanics Reviews，2001，54（4）：331-390.

［3］ 夏天翔，姚卫星.连续体结构拓扑优化方法评述［J］.航空工程进展，2011，2（1）：1-11. XIA Tianxiang，YAO Weixing.A survey of topology⁃optimization of continuum structure［J］.Advances in⁃Aeronautical Science and Engineering，2011，2（1）：1-11.

［4］ 隋允康，叶红玲.连续体结构拓扑优化的ICM方法［M］.北京：科学出版社，2013.

［5］ 赵永辉.大客车车身骨架结构拓扑优化设计［D］.武汉：武汉理工大学，2008.

［6］ SEKULSKI Z.Multi-objective topology and size opti⁃mization of high-speed vehicle-passenger catamaran structure by genetic algorithm［J］.Marine Structures，2010，23（4）：405-433.

［7］ SEKULSKI Z.Least-weight topology and size optimiza⁃tion of high speed vehicle-passenger catamaran struc⁃ture by genetic algorithm［J］.Marine Structures，2009，22（4）：691-711.

［8］ 金咸定，夏利娟.船体振动学［M］.上海：上海交通大学出版社，2011.

［责任编辑：卢圣芳］

Typical shape and topology optimization design of the ship grillage structure

ZHANG Huixin1，2，YANG Deqing1，2
1 School of Naval Architecture，Ocean and Civil Engineering，Shanghai Jiao Tong University，Shanghai 200240，China
2 State Key Laboratory of Marine Engineering，Shanghai Jiao Tong University，Shanghai 200240，China

Taking the typical ship grillage structure as the study object,this paper mainly describes the ap⁃plication of optimized design of ship structures.Specifically,the size and shape optimization is applied onto the grillage structure at the bottom,with the weight of the structure being objective and the stress being the constraint condition.After optimization,the weight has decreased by 15.82%.As for deck grillage,to im⁃prove the spatial layout of the top of superstructure cabins,raise the natural frequency of grillage structure on top,and seek for the optimal distribution of materials,the topology optimization is applied with its static analysis and modal analysis being discussed.Based on the above obtained data,the volume fraction is set as the restriction condition of the model,and the structural natural frequency is set as the objective func⁃tion.Finally,new structure type which optimizes the spatial layout of the top of superstructure cabins are presented,which renders more reasonable material distribution,increases grillage structure's natural fre⁃quency,and meets expected goals.Research shows that,at present,the grillage structure design can be widely used in the topology and shape optimization design technology.

grillage structure；structure optimization；topology optimization；SIMP theory

U662

A

10.3969/j.issn.1673-3185.2015.06.005

http://www.cnki.net/kcms/detail/42.1755.TJ.20151110.1025.010.html期刊网址：www.ship-research.com

张会新，杨德庆.典型船舶板架拓扑与形状优化设计［J］.中国舰船研究，2015，10（6）：27-33，59. ZHANG Huixin，YANG Deqing.Typical shape and topology optimization design of the ship grillage structure［J］. Chinese Journal of Ship Research，2015，10（6）：27-33，59.

2015-03-30 < class="emphasis_bold"> 网络出版时间：

时间：2015-11-10 10:25

国家自然科学基金资助项目（51479115）

张会新，男，1988年生，硕士生。研究方向：船舶结构优化设计理论与方法。E-mail：zhang525054808@sjtu.edu.cn杨德庆（通信作者），男，1968年生，博士，教授，博士生导师。研究方向：船舶振动噪声分析与控制。E-mail：yangdq@sjtu.edu.cn