正方形的一个轨迹问题

晏龙艺

（江西省宜丰中学）

2000 年国家集训队测验题：△ABC 是正三角形，在此三角形内部求满足∠QAB+∠QBC+∠QCA=90°的点Q 的轨迹。

其轨迹是△ABC 的三条高。我们进一步探讨：

问题：四边形ABCD 是正方形，在此正方形内部求满足∠QAB+∠QBC+∠QCD+∠QDA=180°的点Q 的轨迹。

解：如图所示，正方形ABCD 中，E、F、G、H 分别是AB、BC、CD、DA 的中点，连接AC、BD、EG、FH。首先容易验证，若Q 点在线段AC、BD、EG、FH 上，满足∠QAB+∠QBC+∠QCD+∠QDA=180°。

其次，我们证明：Q 的轨迹就是线段AC、BD、EG、FH。

假设Q 点不在线段AC、BD、EG、FH 上，不妨假设Q 点在△ODG 中，而满足∠QAB+∠QBC+∠QCD+∠QDA=180°。作P 与Q关于EG 对称，延长QP 与AC、BC 分别交于K、I，在线段BI 上作一点J，使得IJ=IC，连接QA、QB、QC、QD、QJ，PA、PB、PC、PD、PJ、JK、OQ。

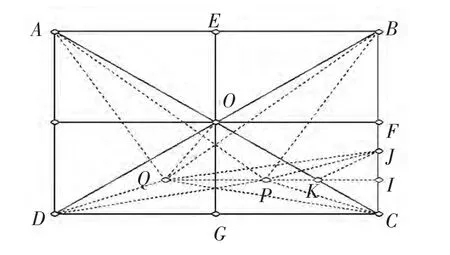
由辅助线作法容易得到，QI⊥BC，∠KJI=∠KCI=45°，四边形ABPQ 是等腰梯形，∠DBQ=∠CAP=∠1，∠QBP=∠PAQ=∠2，∠QDP=∠QCP=∠QJP=∠3，∠QDB=∠PCA=∠PJK=∠4。

∵∠QAB+∠QBC+∠QCD+∠QDA=180°

而∠QAB=45°+∠1+∠2，∠QBC=45°-∠1，∠QCD=45°-∠3-∠4，∠QDA=45°+∠4，将它们代入上式。

∴∠2=∠3

∴B、J、P、Q 四点共圆，又∵四边形ABPQ 是等腰梯形

∴∠BJQ=∠BPQ=∠AQP∴∠BPQ=180°-∠ABP=180°-45°-（∠1+∠2）

又∵∠BJQ=180°-∠QJC=180°-45°-（∠3+∠4）

∴∠1+∠2=∠3+∠4，又∵∠2=∠3∴∠1=∠4

但在△BOQ 中，∠BOQ=135°+∠QOG 为钝角，∴BQ＞OB

在△DOQ 中，∠DQO＞∠DGO=90°为钝角，∴OD＞DQ 而OB=OD，∴BQ＞DQ，∴∠4＞∠1

矛盾！从而命题得证。即Q 的轨迹为线段AC、BD、EG、FH。

我们注意到，2000 年国家集训队测验题中Q 点的轨迹是△ABC 的三条对称轴在△ABC 内部的部分，上面这个问题中Q 点的轨迹是正方形ABCD 的四条对称轴在正方形内部的部分。因此，我们提出问题：

猜想：凸n 边形A1A2A3…An是正n 边形，在此正n 边形内部满足∠QA1A2+∠QA2A3+∠QA3A4+…+∠QAnA1=（n-2）90°的点Q 的轨迹是正n 边形的n 条对称轴在正n 边形内部的部分。

马传渔.最新国际国内数学奥林匹克竞赛优化解题题典［M］.长春：吉林教育出版社，2003-01.