基于DOE敏感性分析的动力总成悬置系统优化

（上汽通用五菱汽车股份有限公司技术中心，广西 柳州 545007）

随着人们对整车舒适性要求的提高，振动与噪声与舒适性要求成为汽车设计最重要的指标之一。道路条件的改善和汽车设计的轻量化，使得发动机成为整车中最大的噪声源和振源。悬置系统作为动力总成与车架或车身间的弹性连接系统，其系统性能设计的优劣直接关系到发动机振动向车体的传递，影响整车的噪声、振动与舒适性(NVH)性能[1]。

在已经确定动力总成基本参数及整车基本参数的前提下，正确匹配悬置的刚度、阻尼系数以及安装位置，合理设置动力总成各阶模态固有频率，保证悬置系统有较高的模态解耦程度，可以最大限度地减小由动力总成引起的振动向车体的传递，提高悬置系统的工作可靠性，改善整车舒适性[2~4]。而悬置的布置往往受到发动机舱布置的限制，安装位置可能会根据布置的需要进行微调。在设计制造时，悬置的刚度和阻尼也会在一定范围内发生变化，因此必须考虑悬置位置、刚度、阻尼和隔振性能的变化，即对悬置系统进行灵敏度分析[5]。近年来，有关于动力总成悬置系统灵敏度分析的文献报道[6-7]。Qatu计算分析了动力总成悬置系统的频率间隔对橡胶悬置刚度的灵敏度。Siraf和Change通过仿真实验研究了悬置系统的解耦率对橡胶悬置刚度、位置和副车架刚度的灵敏度。

本文就悬置系统的匹配进行探讨，对悬置系统的种种约束条件进行详细研究，并利用Matlab编制了悬置优化程序，通过ISIGHT软件和Matlab软件的集成，利用ISIGHT软件的全局优化方法——多岛遗传算法进行确定性优化设计；在确定性设计的基础上，再调用Isight软件中DOE分析模块进行灵敏度性分析，找到了影响主方向模态及能量分布的关键因素，通过刚度调整来达到设计目标，从而解决工程实际问题。

1 动力总成悬置系统简化模型

考虑到动力总成悬置系统的固有振动频率一般低于30 Hz，因此通常将动力总成视为刚体，同时将各个悬置简化为沿空间3个相互垂直方向（即主刚度方向）上的弹性阻尼元件，3个方向的刚度分别表示为Kui、Kvi、Kwi。这样，动力总成悬置系统将构成一个空间六自由度系统，见图1。设动力总成置于相互正交的O点XYZ坐标系中，其中原点0为静止时动力总成的质心。刚体的运动有6个自由度，即x、y、z3个方向的移动x（纵向）、Y（横向）、Z（垂向）和绕x、y、z轴的转角θx（侧倾）、θy（俯仰）、θz（横摆）。

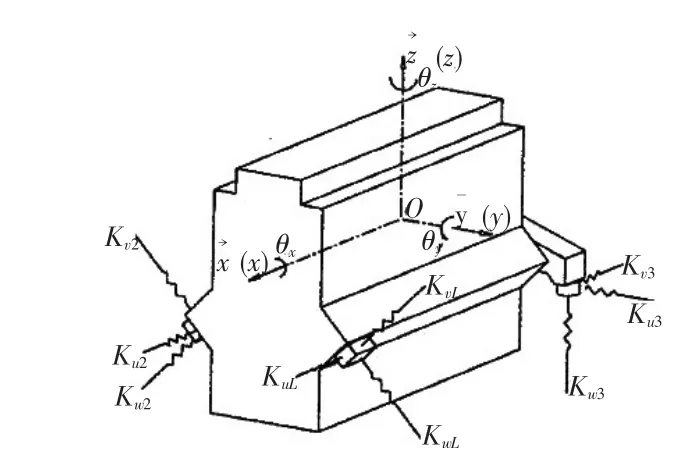
图1动力总成悬置系统动力学模型

其广义坐标为

利用拉格朗日方程和虚功原理可得动力总成悬置系统的振动方程为

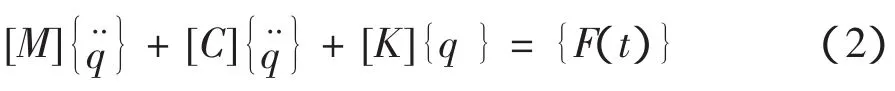
式中：[M]为系统质量矩阵，[C]为系统阻尼矩阵，[K]为系统刚度矩阵，F（t）为激振力，q咬=[x咬,y咬,z咬,θx,θy,θz]T为六个广义加速度列向量。

2 悬置系统优化模型的建立

对于动力总成悬置系统来说，通常它的6个固有振型在多个自由度方向上是耦合的，在某个自由度方向进行激振就会产生耦合振动，这样使得共振频率的范围大大加宽，增大了共振的机会[8]。模态解耦方法是目前悬置参数设计运用较多的方法之一，其假设系统微幅振动（阻尼可以不考虑），通过合理配置刚度矩阵来实现系统的优化。常用的解耦方法有弹性中心法、刚度矩阵解耦法、能量解耦法等。弹性中心法受到悬置布置位置的限制，而刚度矩阵法对于缺少对称面的动力总成结构应用不便，能量解耦法[9~10]则可以在原坐标系中进行解耦设计，基本脱离发动机类型和布置形式，解耦总指标在0~1范围内变化，使优化计算保持较好的稳定性。因此本文对于某研究车型悬置系统采用能量解耦方法。

2.1 目标函数的建立

发动机动力总成悬置系统在微小振幅作用下，可忽略悬置阻尼对悬置动态特性的影响可得动力总成悬置系统6自由度线性自由振动微分方程为

对于式（3），设理论解为

将其代入式（3）可得

由式（4）可得到悬置系统的圆频率及其振型，当悬置系统以第i阶主振动时，第K个广义自由度上分配到的能量所占悬置系统的总能量[10]的百分比为

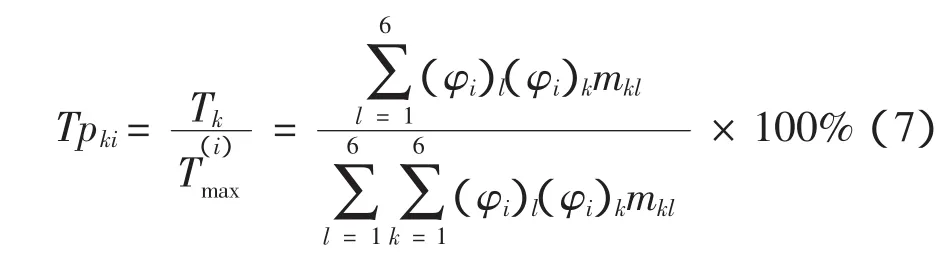
其中：mkl为M的第k行l列元素；φi为系统的i阶主振型；（φi）k、（φi）l分别为φi的第k和第l个元素。Tpki值的大小表征了解耦程度的高低。由于实际布置空间的限制，要实现完全解耦很困难，对于四缸机来说，2阶惯性力和2阶转矩是悬置系统的主要激振力，故主要考虑沿Z方向和绕X轴的解耦状况[9]。目标函数如式（7），其中EZ和ERxx分别为沿Z方向和绕曲轴方向能量百分比最大值。

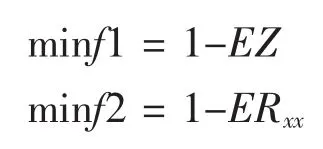
2.2 约束条件和设计变量

本文研究的是橡胶悬置，因为材料和工艺原因，压剪刚度比值应在3~8之间。另外，发动机动力总成的位移不能过大，否则发动机部件会产生碰撞，降低使用寿命，故静位移不得超过6mm。

发动机悬置系统振动特性与发动机的质量、转动惯量及悬置系统的参数(支撑位置、安装角度、支撑元件的刚度和阻尼)有关。动力总成本身的特性一般不改变，因此只选取悬置系统参数作为设计变量。悬置系统参数包括悬置弹性中心的位置、安装角度、悬置元件的刚度和阻尼，阻尼的主要作用是降低共振峰值，并且实际的制造误差不容易控制，一般不作为设计变量。鉴于本文研究的动力总成悬置的安装位置和安装角度基本不能改变，因此，本研究只选取三个悬置的主轴刚度作为优化设计变量。

3 原车悬置系统振动特性分析

本研究车型动力总成悬置系统特性分析和优化所需的相关参数可通过相应的测试和计算获得。表1为各悬置的主轴刚度；表2为各悬置点的位置坐标及安装角度。动力总成的质量是130．9 kg，基于整车坐标系的动力总成转动惯量分别为Ixx=2.801、Iyy=7.466、Izz=7.515、Ixy=0.5398、Iyz=0.2686、Izx=-0.8903，单位为kg·m2.目标汽车采用动力总成中置，后轮驱动型式。

表1原悬置系统主轴刚度（参考整车坐标系）

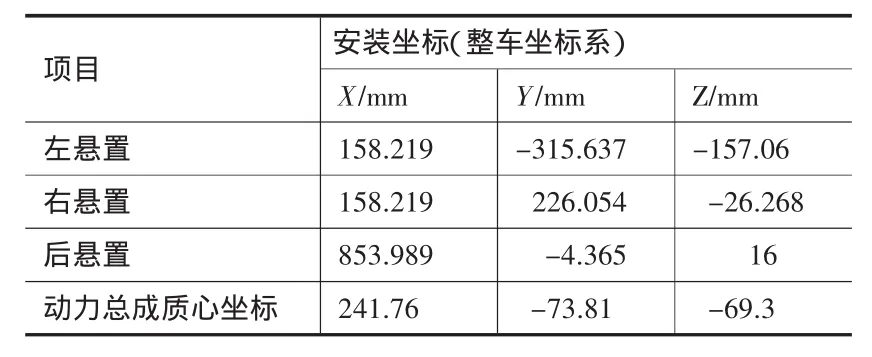
表2悬置安装位置及动力总成质心坐标

将目标动力总成各参数代入动力学模型，利用Matlab软件编制程序进行模态分析，可得到原悬置系统的固有频率和能量分布百分比如表3所示。

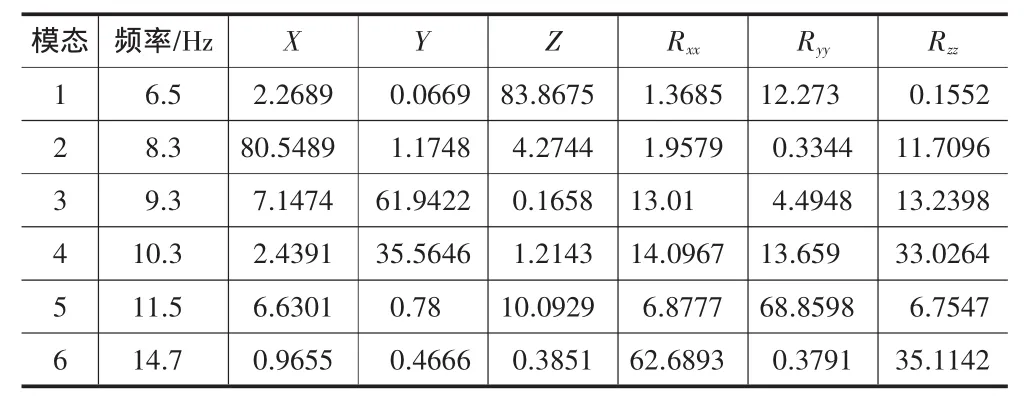
表3原系统固有频率和解耦率分布

由表3可知，系统振动解耦率除了X和Z方向较理想外，其余方向均低于80%。在第3阶模态中X向与Rxx、Rzz3方向较强耦合振动现象，在第4阶模态中Y向与Rxx、Ryy Rzz四向耦合较严重，在第5阶模态中Z、Ryy向耦合程度较高，在第6阶模态中Rxx、Rzz向耦合程度也很高。从频率分布上来看，系统绕曲轴旋转方向的固有频率为14.7 Hz，直列4缸发动机在怠速工况下以2阶转矩激励为主，其激励频率与2阶不平衡力相同，考虑怠速工况，研究车型发动机怠速转速为850 r／min，可计算得其激振频率为28.3 Hz.根据隔振原理，系统绕曲轴旋转的固有频率应该控制在怠速激振频率的1／2在之下才能具有隔振效果，所以Rxx向固有频率应低于14．2 Hz.显然，这里Rxx向频率14.7已超过1/2怠速激振频率，不利于对怠速工况的隔振。这与实车测试时驾驶室座椅导轨异常振动的现象非常吻合，因此对该悬置系统模态频率进行解耦优化配置。

4 基于遗传算法的悬置系统全局优化

多岛遗传算法（Multi-Island Genetic Algorithm,MIGA)建立在传统遗传算法（Traditional Genetic Algorithm，TGA)基础上。多岛遗传算法不同于传统遗传算法的特点是每个种群的个体被分为几个子群，这些子群称为“岛”，传统遗传算法的所有操作分别在每个岛上进行，每个岛上选定的个体定期地迁移到另外岛上，然后继续进行传统遗传算法操作。多岛遗传算法进化流程如图2所示。迁移过程由两个参数进行控制，分别为迁移间隔和迁移率，迁移间隔表示每次迁移的代数，迁移率决定了在一次迁移过程中每个岛上迁移的个体数量的百分比。迁移率的选取是一个很复杂的问题，由于被迁移者一般均是各子群体中的最优个体，所有迁移率较大，则有利于优良个体在整个群体中的传播和收敛速度的提高，但同时也会增加通信的开销，使加速比下降，也可能导致群体多样性下降，不利于算法在多个方向同时进行搜索的特征。迁移间隔小有利于群体之间的融合，使得优良个体及时传播到所有子群体中，对群体的进化方向可以起到良好的指导作用，有利于提高解的精度和全体的收敛速度。但同时也会明显增大通信以及同步开销，不利于加速比的提高，某些优良个体在全体中的统治地位会产生不利于全体保持多样性的负面影响。如果迁移间隔过大，则会起到相反的作用。多岛遗传算法中的迁移操作保持了优化解的多样性，提高了包含全局最优解的机会。多岛遗传算法在优化过程中首先利用初始值进行优化操作，初步达到收敛后，由于变异和迁移作用，在一个新的初值点开始重新进行遗传操作，如此反复操作，尽可能避免局部最优解，从而抑制了早熟现象的发生。

多岛遗传算法的示意图如下，遗传算法在解决“多峰”或“多谷”的优化问题时存在很大的算法优势。

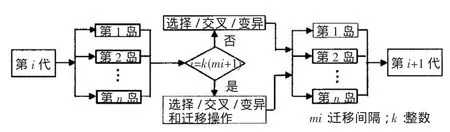
图2多岛遗传算法示意图

本文通过编制Matlab优化程序，结合Isight软件，设置后目标函数和约束条件，以3个悬置的9个刚度为设计变量，调用Isight软件中的多岛遗传算法及常规梯度优化算法对研究车型悬置系统进行了优化[10]，通过迭代计算可获得针对悬置9个主轴刚度变量的优化结果（见表4），此时，系统振动解耦情况如表5所示。

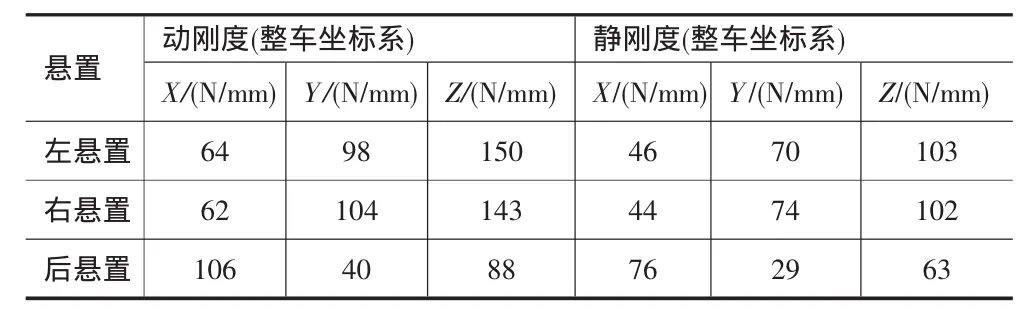
表4优化后悬置系统主轴刚度

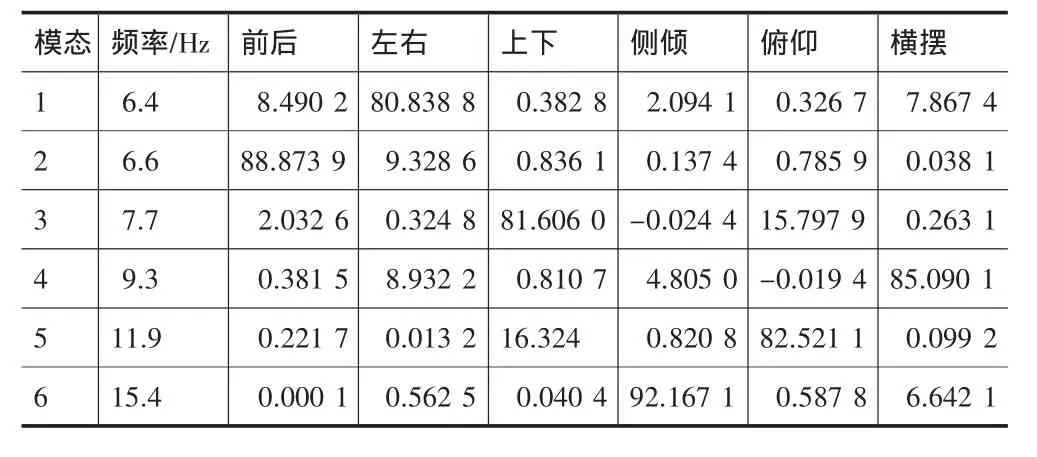
表5优化后系统固有频率及解耦率

从表4、表5的对比中可以看出，优化后固有频率分布在6.4～15.4 Hz之间，各自由度上的解耦率都超过了80%，各方向的耦合振动情况得到了很大的改善。多岛遗传优化对动力总成3个悬置件各主轴刚度的调整，达到了对悬置系统6个自由度解耦率最大的优化目的，取得了较好效果。但绕曲轴模态比原系统还高达到了15.4，没有达到预期目标。需要进行DOE敏感性分析来进一步优化。

5 基于DOE的悬置系统敏感性分析及优化

DOE，即试验设计（Design Of Experiment)，是研究和处理多因子与响应变量关系的一种科学方法。它通过合理的挑选试验分析，从而找到总体最优的改进方案。悬置系统的DOE分析采用中心复合设计方法，以此获得关键因素对悬置系统主要性能的影响：第一，系统垂向与绕曲轴方向的模态；第二，系统垂向与绕曲轴方向能量解耦率；第三，系统最小与最大固有频率等。本文中采用DOE敏感性分析获得三悬置的9个主轴刚度对绕曲轴方向的模态的影响因素大小，通过合理的调整，在降低Rxx模态的同时保证各方向的解耦率最大化。

用同一Matlab优化程序，联合Isight软件，调用DOE优化模块，设置表5中每个悬置各向主轴刚度变动范围为±15%，以各方向能量最大化以及Rxx模态频率最小为设计目标，在这样一个范围内，研究悬置系统关键目标与各因素的关系。采用拉丁方方法经过10次迭代后，获得各刚度因子对Rxx模态的敏感度如图3所示。

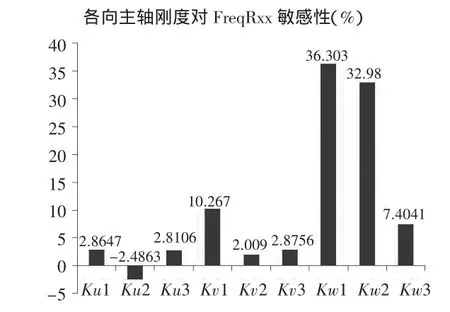
图3各悬置主轴刚度对Rxx模态的影响

由图3中绕曲轴扭转方向固有频率FreqRxx变动与各因素的关系可知，Kv1、Kw1、Kw2、Kw3 对 FreqRxx频率有显著影响，尤其是Kw1和Kw2敏感性最大。综合结果，因此若要降低FreqRxx，降低Kw1的值最为有效，其次是Kw2。经过调整后最终各主轴刚度见表6，表7是最终的系统振动解耦情况。

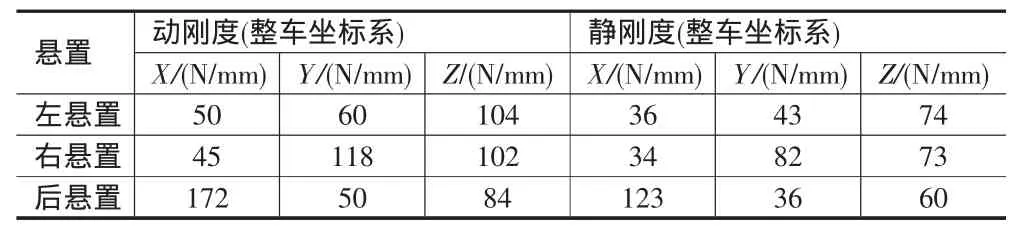
表6优化后悬置系统主轴刚度

表7优化后系统固有频率及解耦率

从表7优化前后的频率对比中可以看出，优化后绕曲轴频率降低到13.1 Hz，小于了1/2怠速激振频率，频率分布也有所改善。各方向的解耦率仍然满足要求。从实车测试来看，驾驶室座椅导轨的振动幅值大幅下降（图4），达到了设计目标。

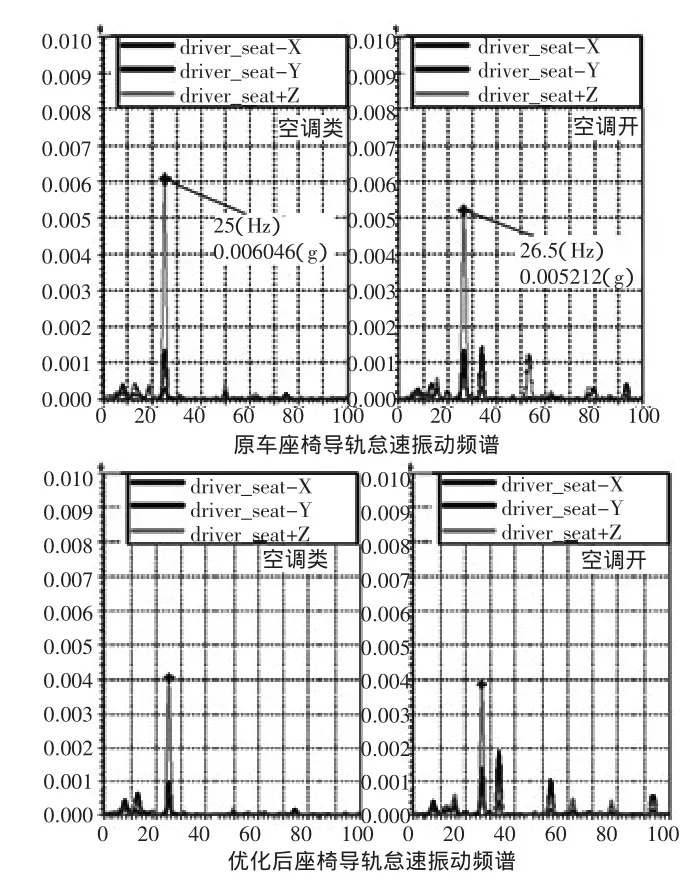
图4优化前后座椅导轨振动频谱对比图

6 结束语

动力总成橡胶悬置系统的刚度匹配是整车开发的一项关键技术，悬置系统的匹配好坏与整车振动密切相关。本文以发动机悬置系统能量解耦及模态分布为目标，悬置刚度参数为设计变量，考虑目标函数和约束函数对于悬置刚度参数的灵敏度，构造了多目标优化数学模型，编制Matlab优化程序。结合ISIGHT软件，采用多岛遗传优化算法对一款发动机悬置系统的悬置刚度参数进行了优化设计，并用DOE技术进行了敏感性分析，找到了影响主方向模态及能量分布的关键因素，通过刚度调整，达到了设计目标。经过优化前后测试数据的对比发现经过灵敏度分析所得到的结果能有效的改善悬置系统的隔振性能，为进一步优化动力总成悬置系统提供了理论基础。

[1]Tamboli J A，Joshi S G.Optimum Design of a Passive Suspension System of a Vehicle Subjected to Actual Random Road Excitations[J]．Journal ofSound and Vibration，1999，219(2)：193－205．

[2]Kim W D，Lee H J，Kim J Y，et a1．Fatigue Life Estimation of an Engine Rubber Mount[J]．International Journal of Fatigue，2004(26)：553560．

[3]Johnson SR，Subhedar JW．Computer Optimization of Engine Mounting Systems[C]．SAE，1997．

[4]J Geek P E，Patton R D．Front wheel Drive Engine Mount Optimization[C]．SAE，1984．

[5]樊逸斌.基于灵敏度分析的悬置系统设计及优化[J]．汽车科技，2010（6）：17－20.

[6]Qatu，Sim M，Johns F．Robustness of powertrain mount system for noise，vibration and harness at idle[J]．Proc．Instn Mech．Engrs，Pan D，Journal of Automobile Engineering，2002，216：805－8l0．

[7]Sirafi M，Chang Y P．Robustness of mount systems for idle NVH，Pan 1：center of Gravity(cG)mounts[J]．Internaltional Journal of Vehicle Noise and Vibration，2006，2(4)：317 －333．

[8]陈 剑，徐陈夏．发动机悬置系统优化设计及其可靠性分析[J]．汽车工程，2009，31(3)：234－238．

[9]吕兆平．能量法解耦在动力总成悬置系统优化设计中的运用[J]．汽车工程，2008，30(6)：523－526．

[10]侯 勇，赵 涛．动力总成悬置系统解耦设计[J]．汽车工程，2007，29(12)：1094－1097．

[11]史文库，洪哲浩，赵 涛，汽车动力总成悬置系统多目标优化设计及软件开发[J]．吉林大学学报(工学版)，2006，36(9)：654－658.

[12]吕兆平.某大微客动力总成悬置系统优化设计研究[D].湖南大学硕士学位论文，2010.