基于全阶模型的异步电机磁链观测 收敛性分析与对策

邓 歆 张广明 王德明 梅 磊 欧阳慧珉

（南京工业大学自动化与电气工程学院 南京 211816）

1 引言

交流驱动系统中，传统的V/F 控制方式以其简单实用，不依赖电机参数等特点受到广泛的使用，但它存在在低速区域的带载能力减弱、速降增大、动态与稳态特性下降等缺点，使其应用范围受到限制。尽管很多学者提出了改进型的V/F 控制方式[1,2]，系统在快速性与稳态精度方面仍然不能让人满意。

矢量控制与直接转矩控制这两种代表当今最先进的变频调速控制方法自从被提出来以来一直是各 国学者的研究热点[3,4]，它们实现了对电机的高性能控制，系统的各项性能指标都有很大的改善，但它们共同需要对电机磁链进行观测。矢量控制系统中，最直接简单的是采用电流模型对转子磁链位置信号进行观测，该模型依赖电机转速，适用于中低速区域[5]；而在直接转矩控制系统中，电压模型磁链观测器则受到青睐，利用该模型观测定子磁链，该模型不涉及电机转速，存在纯积分问题，适用于高速区域[6,7]。

鉴于电流模型与电压模型这两种最基本的估计模型存在各自的问题，近年来，全阶模型受到越来越多关注，相应的文献发表了很多[8-22]。全阶模型以电机本身作为参考模型，构建电机状态方程，引入状态反馈矩阵，基于自适应理论对电机进行估计，它同时实现了电机转速作为参数的在线辨识以及电机电流与磁链作为状态变量的实时观测。文献[10]认为通过反馈矩阵的不同配置，全阶模型在稳态时可以等效为电流模型或电压模型，而文献[11]则提出了通过设计反馈矩阵，全阶模型可以在电流模型与电压模型之间的平滑切换。

目前，关于全阶模型的文献研究主要集中在反馈矩阵设计、转速自适应律设计与稳定性研究以及多参数同时辨识策略等方面。为了加快磁链观测器对状态变量的收敛速度，文献[12,13]都提出了将磁链观测器的极点设计在电机极点左边，使得磁链观测器比电机收敛速度更快。而对于全阶模型的稳定性分析主要通过考察辨识转速是否收敛于实际转速进行的，它以电流作为中间量，电机观测磁链幅值认定为恒定[14-17]。事实上电机电磁系统中，转子磁链的变化比定子电流以及q 轴电流误差信号慢很多，Harnefors 提出了通过考察观测磁链是否收敛与实际磁链来分析全阶磁链观测器的稳定性[18]，通过分析二阶磁链误差状态方程的稳定性来分析观测器的稳定性，提出了低速回馈发电状态下电流误差旋转角度的设计方法，保证了全阶磁链观测器的稳定性。

文献[19,20]利用全阶磁链观测器实现了电机转速与定子电阻的同时辨识，基于Popov 超稳定性理论推导出了电机转速与定子电阻PI 自适应律，其中观测电流矢量与实际电流矢量的内积作为定子电阻在线辨识的自适应信号。文献[21]对全阶磁链观测器的电机转速与定子电阻同时辨识的稳定性进行了深入研究，得到了不稳定范围，并提出了改进办法。Kubota 提出了通过在电机的转子磁链轴上加低频抖动电流使得转子磁链幅值产生波动，实现了电机转速与转子电阻的同时在线辨识[22]。

然而关于全阶模型在估计电机系统中参数与变量的过程中，被估计量跟随实际量的收敛速度问题，至今没有看到过相关文献报道。Harnefors 对降阶模型收敛性分析做了大量的研究工作。它在同步旋转坐标系下建立磁链观测器，对传统电压模型磁链观测器、改进电压模型磁链观测器、电流模型磁链观测器以及无功功率模型的收敛特性进行了分析比较，得出电流模型磁链观测器是唯一一个具有线性化特性的磁链观测器，而传统的电压模型磁链观测器存在收敛速度慢，容易受到扰动的缺点[23]。

本文将对全阶模型在估计异步电机参数与变量过程中的磁链收敛特性进行研究。由于全阶模型的非线性特性，本文采用奇异摄动理论，将全阶模型分解为转速辨识模型与磁链观测模型，两个模型在时间尺度上分离，通过分析磁链观测子系统中系统特征值的分布与阻尼特性研究了磁链观测的收敛性与影响收敛速度的影响因子。研究结果表明磁链系统在中高速的阻尼特性需要改善，并提出了改善收敛性的对策。

2 异步电机与全阶模型

所设计的全阶模型将用于矢量控制系统中，电机观测磁链为转子磁链，本文将采用异步电机的反Г 形模型进行研究，如图1 所示，在任意参考坐标系中，以定子磁链与转子磁链矢量作为状态变量构造的电机状态方程如式（1）所示。

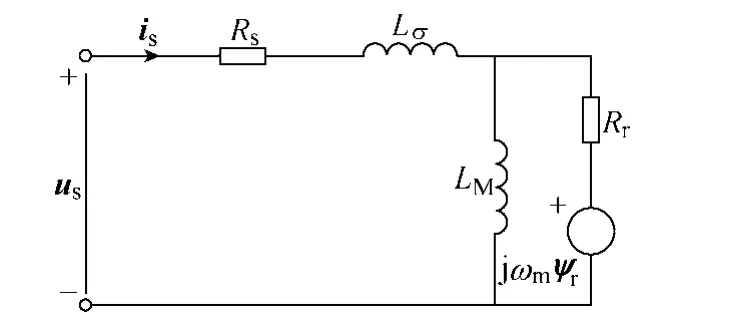
图1 异步电机反Г 形模型 Fig.1 Inverse Г model for induction motor

式中

us——定子电压矢量；

ψs,ψr——定、转子磁链矢量；

Rs,Rr——定、转子电阻；

LM,Lσ——互感和总漏感；

ωk——任意旋转坐标系角频率。

异步电机全阶模型的原理如图2 所示，它以电机本身为参考模型，构建电机状态方程，引入状态反馈矩阵，基于自适应理论对电机进行估计。基于自适应的异步电机全阶模型可以表示为

图2 全阶模型原理图 Fig.2 Full model scheme

式（2）中包含估计转速mˆω ，基于波波夫超稳定性理论或者构建李雅普诺夫函数得到如式（3）所示的全阶磁链观测器转速辨识公式为[12,15,19,20]

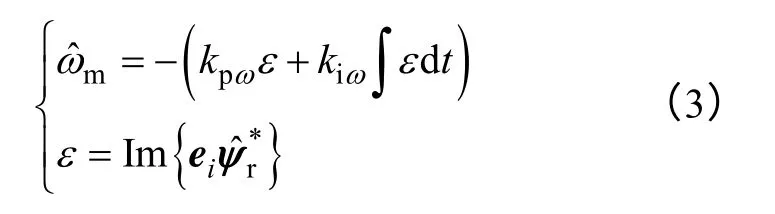
式中，ε,kpω,kiω分别为转速自适应信号，转速辨识比例系数，转速辨识积分系数；为的共轭；Im{ }为取复数的虚部。

式（1）与式（2）相减得到的误差方程为

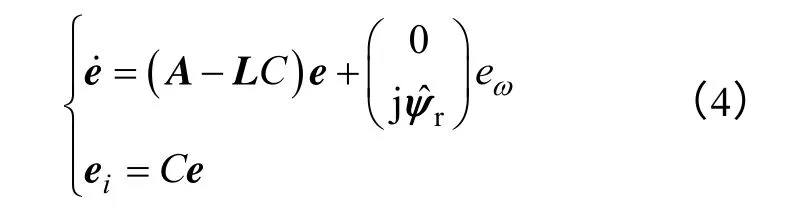
3 全阶模型分解

全阶模型中，转速是作为电机的参数进行 PI自适应律辨识得到，而磁链是作为状态变量观测得到，整个系统为非线性，强耦合的，为了便于分析系统的收敛性，现将系统进行分解。

式（4）与式（2）分别所示的转子磁链与电流误差进行展开可以表示为

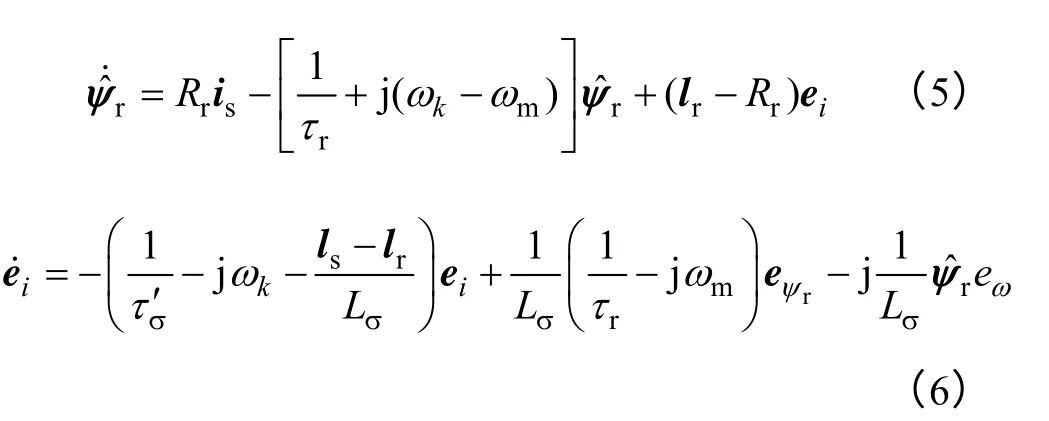
异步电机的实际与观测转子反电动势分别为

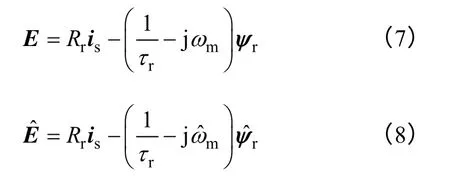
式（7）与式（8）的反电动势误差为

考虑到电流的收敛速度远大于磁链收敛速度，可以认为电流误差达到稳定状态，将式（9）代入式（6）得到

将式（10）代入式（5）可以得到最后的转子磁链观测表达式为

在以观测转子磁链定向的坐标系中，忽略转速辨识的比例部分，将式（10）代入式（3）可以得到式（12）所示的基于反电动势误差的转速辨识公式，同时将式（11）展开可以得到式（13）所示的转子磁链幅值与角频率观测公式。

式（12）与式（13）为全阶模型估计电机转速与磁链的数学模型表达式，将式（12）展开可以得到

文献[17]对转速PI 自适应律系数的整定方法进行了研究，研究表明积分系数kiω影响到辨识转速与实际转速的误差大小，该值设计的较大。因此对比式（13）与式（14）中估计变量前的系数可以发现，当转速辨识系数选取比较大时，辨识转速比观测磁链的动态响应更快，达到稳态的时间更短，根据奇异摄动理论，可以将它们在时间上进行分离。

4 电机磁链系统收敛性分析

整个全阶模型分解为转速辨识模型式（12）与磁链观测模型式（13），它们在时间尺度上分离，可以独立分析其特性。当分析转速辨识模型时，观测磁链可以认为恒定不变；当分析磁链观测模型时，辨识转速可以认为迅速收敛达到稳态，接近实际转速。

从双时间尺度角度出发，在磁链观测系统中可以认为辨识转速达到稳态，即令式（12）等于零可以得到

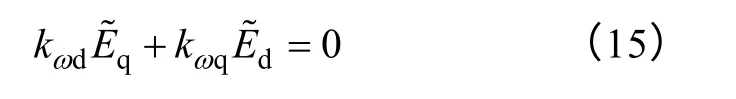
通过式（16）可以得到辨识转速与实际转速之间的关系表达式为

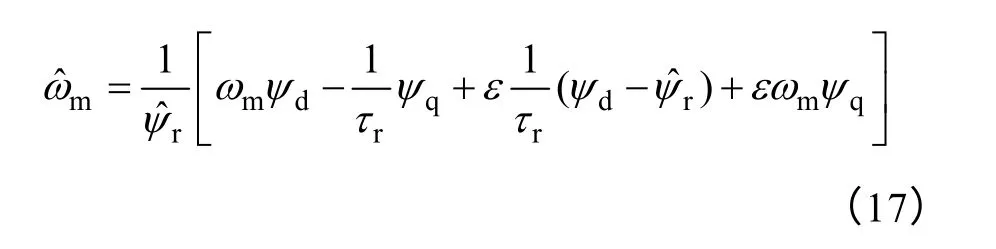
为此，分析观测磁链收敛于实际磁链的情况，电机实际转子磁链可以通过电流模型表示为

将式（18）展开得到电机实际磁链为

将式（13）所示的磁链观测系统所得到的磁链信息用于电机控制时，电机实际磁链系统中的同步频率ωe由式（13）所估算出，观察发现式（13）所示的观测系统发现，观测器需要用到电机的实际反电动势Ed，Eq，因此观测系统与电机实际系统构成了一个闭环结构。

为了考察观测磁链收敛性能，将式（16）所示 的反电动势误差代入式（13），这样观测模型中就不包括辨识转速，得到式（20）所示的观测 系统。

将式（20）代入式（19）可以得到观测磁链系统与电机本身构成的磁链闭环系统，考虑到磁链的非线性动态过程，存在关系式

式中

式中

观察式（22）状态方程矩阵H 发现：电机d、q轴实际磁链与观测磁链之间存在严重的耦合，耦合项与电机的q 轴实际电流以及电机转速有着密切联系。当转矩电流iq很小时，d 轴磁链误差的动态响应不受q 轴磁链的影响。

整个磁链系统的动态特性取决于状态方程H 的特征值分布，因此将研究状态方程H 的特征多项式f(s)如式（23）所示。

从特征多项式可以发现：特征值有三个，一个为常数-1/τr，其余两个取决于后面二次多项式的配置，该多项式与电机的转矩电流以及电机转速有关外，还受到系数kd、kq、ε 的影响，而这些都取决于全阶模型反馈矩阵的配置，因此本文后续都只针对该二次多项特征式进行研究。

反馈矩阵为零，式（23）所示多项式的特征值轨迹图如图3 所示，电机转速变化范围为3～1 500 r/min，箭头方向为转速递增方向。

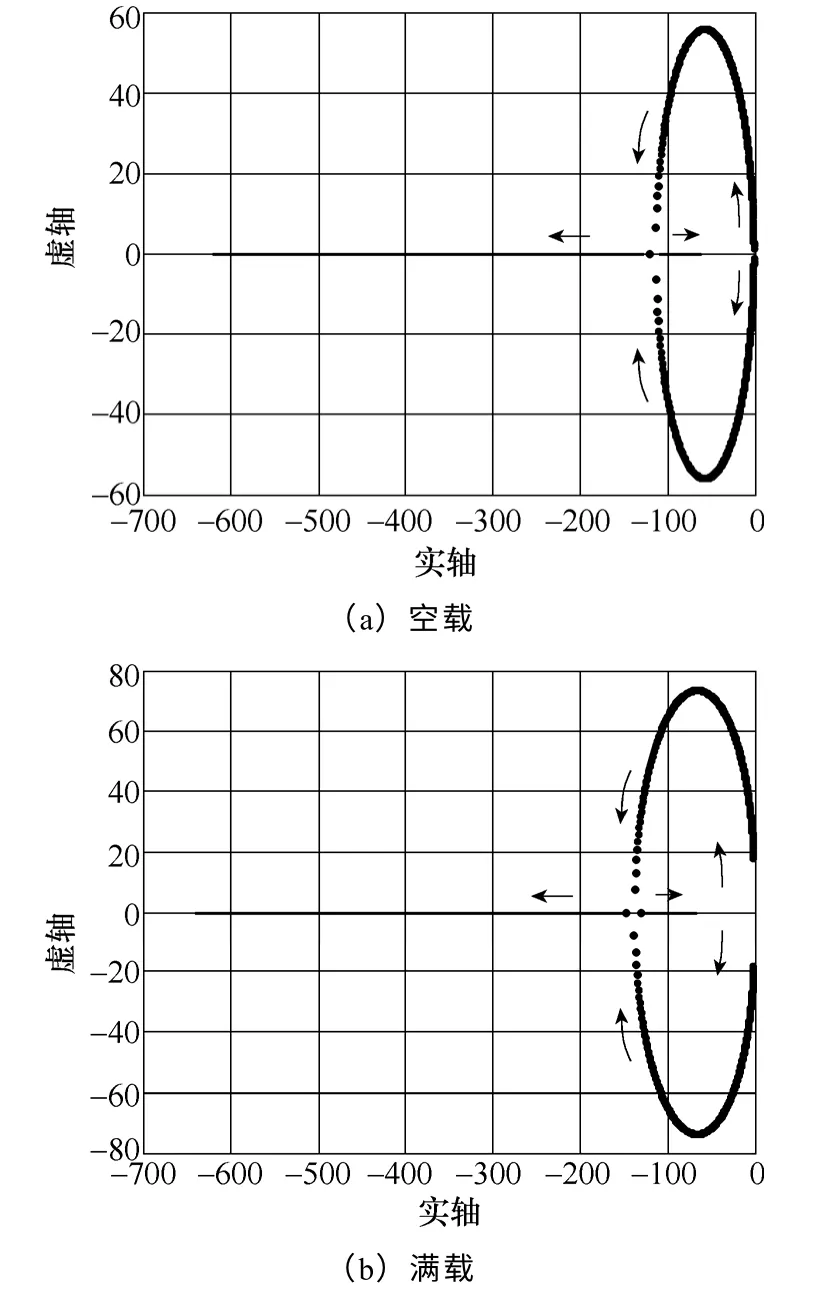
图3 反馈矩阵为零，磁链观测系统特征根轨迹图 Fig.3 Eigenvalue loci figure for flux observation system with null feedback matrix

从图3 可以看出电机在空载与满载情况下，特征值轨迹图相似。低速区域，系统特征值的阻尼为欠阻尼，系统调整时间稍长，阻尼比略小于最佳阻 尼系数；随着转速逐渐递增，系统特征值变为 实数，二阶系统为过阻尼系统，系统响应变慢。相对而言，磁链系统在中高速区域内的阻尼比更远离 最佳阻尼系数，因此磁链系统在中高速区域内 的收敛性要差于低速区域。

5 改善磁链系统收敛性对策

式（23）给出了基于全阶模型的观测磁链与电机实际磁链构成的闭环系统特征方程，为了改善全阶模型的观测性能，有必要对特征方程进行研究，式（24）所示的二次特征多项式为研究对象

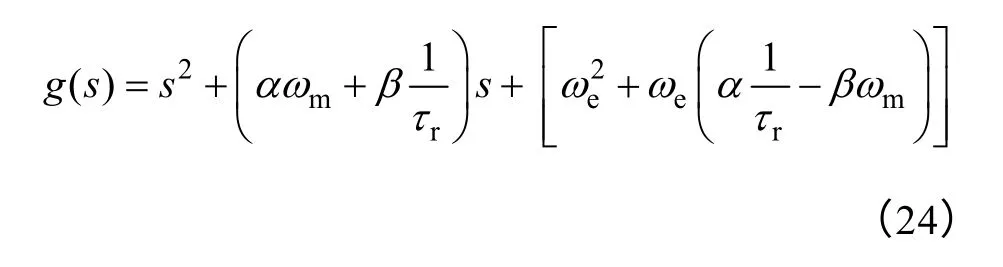
ωn——自然振荡频率，

将α 与α 值代入ωn与ξ 可以得到

从以上可以发现：电机在中高速区域内的阻尼系数几乎与电机转速成正比，当电机转速较大时，磁链系统呈现过阻尼特性；而当电机在低速区域内时，相对应的系统阻尼较小，呈现欠阻尼特性，阻尼系数比 存在最小值，该值比最佳阻尼系数略小，也就是说低速区域的阻尼系数在最佳值附近徘徊，这与图3 所示的系统根轨迹结果吻合。因此要改善整个速度区域内磁链系统的阻尼特性应当选择在中高速区域减小阻尼系数。

（1）电机定子电阻与转子电阻的阻值通常相差不会太大，观察α 值表达式的特点，可以发现：为了

（2）为了确保阻尼系数为正，系统稳定，上式中α 值应尽量与ωm极性相同，观察α 值的特点，可 0 时，α 与ωm极性相同，其中Rg1为一个正常数。

（3）对于阻尼系数进一步有简化公式ξ≈ 以发现：电机漏感很小，当令，为了保证系统的阻尼尽量在最佳阻尼 值附近，当α 值中分子随着转速增大而增大， 分母也应该随着转速进行增长，因此可以令sdl =，其中Rg2为一个正常数。

综合以上分析可以总结出：为了简化设计，令Rg1与Rg2相同，即同时可以令，其中Rg为一个正常数，该值的大小可以根据电机的实际定子电阻与转子电阻值进行设计。

图4 所示的是改善后的磁链系统根轨迹图，从图中可以发现，系统的阻尼值基本维持在最佳值附近不发生变化。该反馈矩阵设计方法与文献[8]中改善电机转速辨识性能所提出的方法类似，这说明了基于全阶模型的电机磁链系统与转速辨识系统互相耦合，性能之间互相影响，反馈矩阵的设计方法将同时影响磁链观测收敛性能与转速辨识的动态性能，从磁链收敛性能与转速辨识动态性能两个方面着手设计的性能改善方法能得到相似的反馈矩阵设计方法。

图4 采用反馈矩阵设计，磁链观测系统特征根轨迹图 Fig.4 Eigenvalue loci figure for flux observation system with proposed feedback matrix

6 仿真及分析

为了验证本文反馈矩阵对全阶模型的磁链收敛特性分析以及所提出的反馈矩阵设计方法正确性与有效性，进行基于全阶模型的异步电机矢量控制系统仿真。

图5 为基于全阶模型的异步电机矢量控制系统控制框图。表1 所示的为仿真用到的2.2kW 电机参数，电机额定电流为6.9A，额定电压380V。

图5 基于全阶模型的矢量系统控制框图 Fig.5 Control scheme for full model based vector control system

表1 感应电机参数 Tab.1 Parameters of induction motor

转子磁链的给定值为0.88Wb，电机在前1s 进行直流励磁，电机速度给定为零，电机实际磁链与观测磁链都收敛为给定值。1s 钟进行转速指令给定。给定转速1 200r/min、600r/min 以及30r/min 时的电机转速与辨识转速，实际磁链与观测磁链对比图依次如图6～图8 所示。

从图6～图8 的a 图可以发现：当电机运行于中高速区域时，电机的观测磁链与辨识转速在瞬态过程中都有一定的振荡，磁链稳定的时间长；而低速区域的振荡相对较小，磁链稳定的时间短。

图6 给定转速1 200r/min 时，电机转速与辨识转速、 实际磁链与观测磁链对比 Fig.6 Comparison between actual and identified speed,actual and observed flux with reference speed 1 200r/min

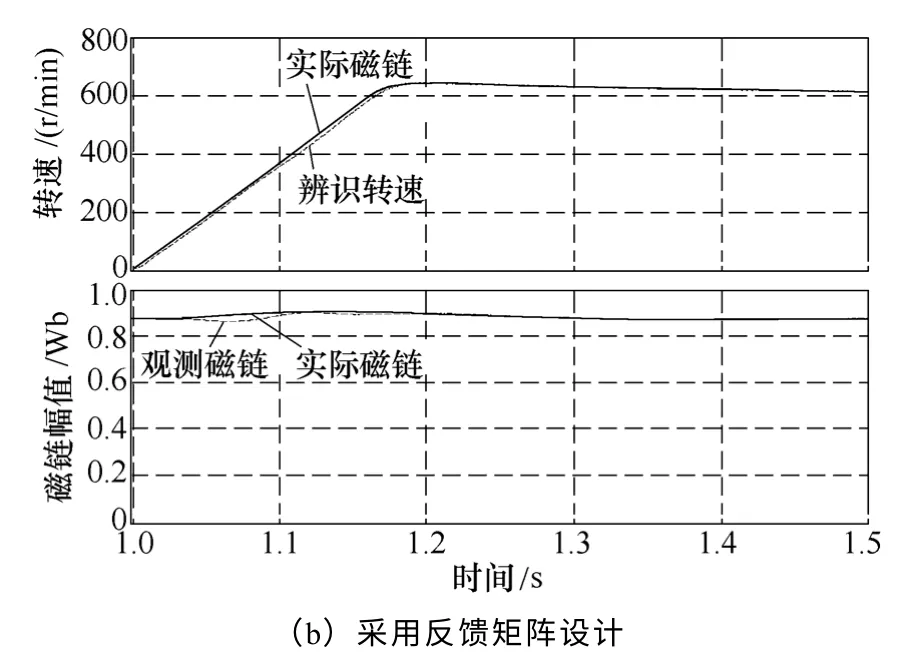
图7 给定转速600r/min 时，电机转速与辨识转速、 实际磁链与观测磁链对比图 Fig.7 Comparison between actual and identified speed,actual and observed flux with reference speed 600r/min

图8 给定转速30r/min 时，电机转速与辨识转速、 实际磁链与观测磁链对比图 Fig.8 Comparison between actual and identified speed,actual and observed flux with reference speed 30r/min

图6 ～图8 的图b 中，采用反馈矩阵设计后，电机中高速区域观测磁链与转速在瞬态过程中的振荡现象基本消失，这是因为加入反馈矩阵设计后，中高速区域的阻尼特性有很大改善；低速区域，辨识转速也能很好地跟随实际转速没有滞后，电机实际磁链与观测磁链基本重合。

表2 给出了电机在高中低速三个区域在有无反馈矩阵时，磁链收敛稳定时间对照关系。通过表格数据可以发现，无论是有无反馈矩阵，电机在高中低速区域的磁链收敛时间是随着转速越高，收敛时间越长；加入反馈矩阵后，电机在高中速区域收敛时间有很大幅度的缩减。因此本文对高中低速区域磁链收敛性的分析是正确的，提出的反馈矩阵对改善收敛性是有效的。

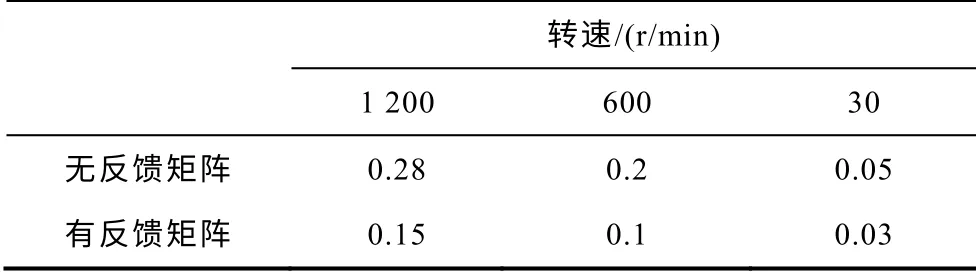
表2 磁链收敛时间 Tab.2 Flux convergence time （单位：s）

7 实验及分析

实验硬件平台如图8 所示，其中功率模块选用三菱公司生产的智能功率模块PM25RSB120，逆变器的死区时间设置为3.2μs，母线电压为540V；控制板是以TI 公司生产的TMS320F2407 为控制芯片，主要负责电流与转速检测信号的采集，PWM 驱动信号的产生与输出。图9 所示的是整个全阶模型的数字化软件实现流程图。

图8 硬件平台 Fig.8 Hardware platform

图9 全阶模型数字化软件实现流程图 Fig.9 Digital realization flow chart of full model

由于电机实际磁链无法检测得到，无法从实验直接验证磁链系统的收敛性。但从文中的分析可以知道：观测磁链与辨识转速收敛于实际值时的收敛性是一致的，即当观测磁链收敛于实际值时，辨识转速才收敛于实际转速，反之亦然。因此可以采用检验全阶模型的辨识转速收敛于实际转速的收敛速度来达到检验磁链的收敛性目的。

实验分为高速 1 200r/min 给定阶跃以及中速600r/min 正反转，低速区域30r/min 由于受到逆变器非线性以及电机参数等的影响较大，不便分析转速的收敛性能，因此低速区域收敛性实验采用观察600r/min 正反转过程穿越低速区域的收敛性，而中速600r/min 区域的可以通过考察电机在反转过程中的特性进行。电机负载为半载，全阶模型反馈矩阵为零以及采用所提出的设计方法后，电机实际转速与辨识转速对比图分别如图10 和图11 所示。

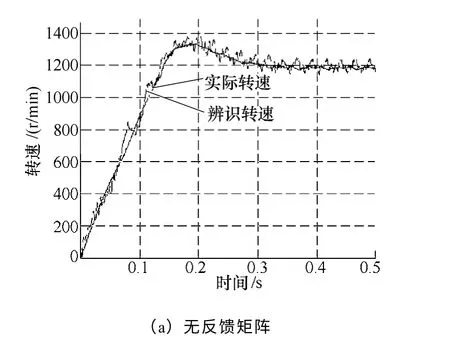
图10 给定转速1 200r/min，实际转速与辨识转速对比 Fig.10 Comparison between actual speed and identified speed with reference speed 1 200r/min

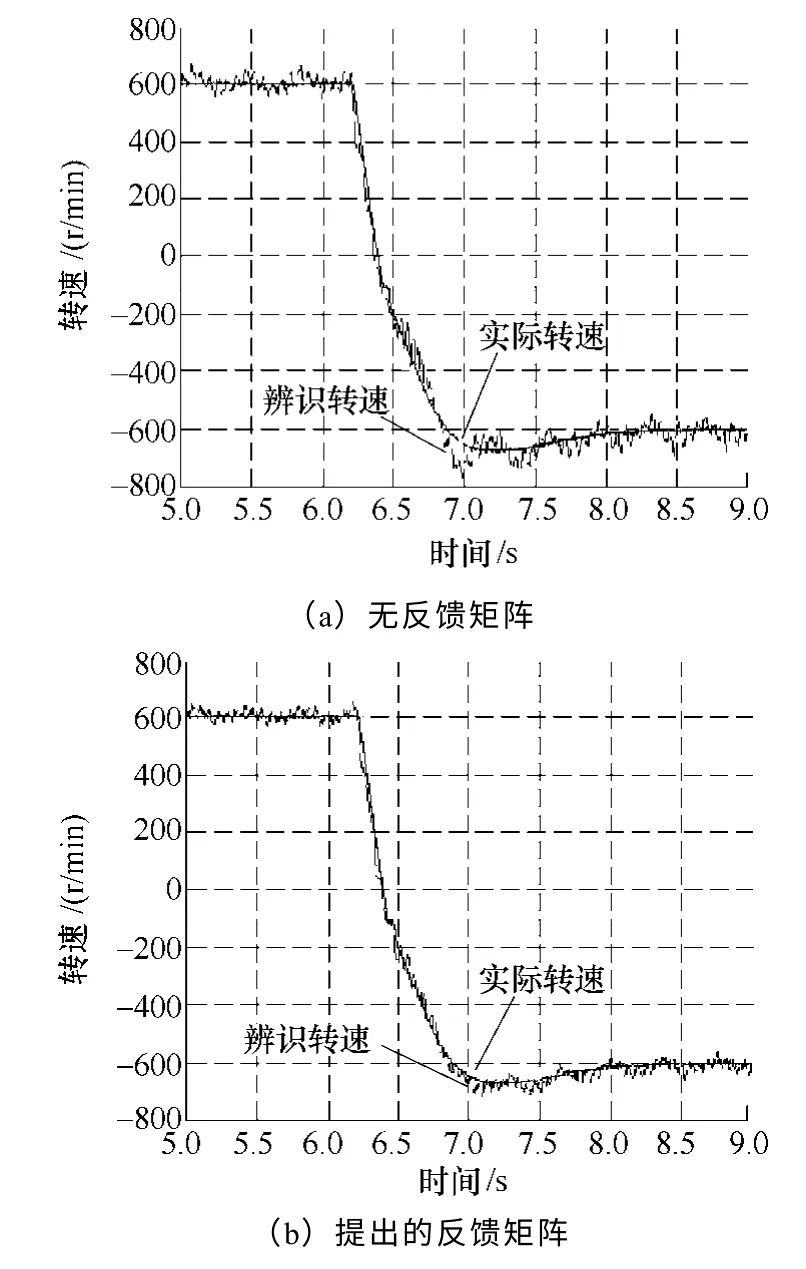
图11 600r/min 正反转时，实际转速与辨识转速对比 Fig.11 Comparison between actual speed and identified speed with reference speed 600r/min forward and inverse rotation

从图10 与图11 中的a 图可以发现，当反馈矩阵为零时，基于全阶模型的控制系统在高速区域以及中速区域内，辨识转速在动态跟随实际转速的过程中都有一定幅度的振荡，并且收敛的时间也偏长，其中给定1 200r/min 阶跃相应中辨识转速在0.15s以后基本收敛，给定600r/min 正反转相应中辨识转速从6.5s 开始到7.5s 后基本收敛，收敛时间在0.1s左右。600r/min 正反转穿越低速区域时，辨识转速基本能很好地跟随实际转速，振荡非常小。

从图10、图11 的b 图中，采用了所提出的反馈矩阵设计后，系统情形有所改观。系统中辨识转速跟随实际转速的性能更好，动态过程中的振荡幅度减小，辨识转速收敛于实际转速的时间也越短，其中给定1 200r/min 阶跃相应中辨识转速在0.08s以后基本收敛，给定600r/min 正反转相应中辨识转速在6.9s 开始到7.3s 之间有小幅度振荡，然后很快收敛于实际值，收敛时间大约0.4s。600r/min 正反转穿越低速区域时，辨识转速能很好地跟随实际转速，振荡几乎不存在。

因此当采用了反馈矩阵设计后，可以认为观测磁链在跟随实际磁链的过程中收敛性也更好，磁链收敛时间缩短，实验结果与上节仿真结果一致，它表明了本文所提出的设计方法是正确与可行的。

8 总结

本文对全阶模型在估计异步电机参数与变量过程中的磁链收敛特性进行研究。采用奇异摄动理论，将全阶模型分解为转速辨识模型与磁链观测模型，两个模型在时间尺度上分离，通过分析磁链观测子系统中系统特征值的分布与阻尼特性，研究了磁链观测的收敛性与影响收敛速度的影响因子。研究结果表明磁链系统在中高速的阻尼特性需要改善，并提出了改善收敛性的对策。

[1] 沈安文,张侨.基于补偿策略的通用变频器高性能控制方法研究[J].电气传动,2007,37(1):16-18.

Sheng Anwen,Zhang Qiao.Compensation strategy based research on high performance control method of general purpose[J].Electric Drive,2007,37(1):16-18.

[2] Garcia M,Lipo T A,Novotny D W.A new induction motor V/f control method capable of high-performance regulation at low speed[J].IEEE Transactions on Industry Applications,1998,34(4):813-821.

[3] 刘洋.高性能主轴感应电机驱动系统研究与开发[D].武汉:华中科技大学,2009.

[4] 张兴华,孙振兴,王德明.电动汽车用感应电机直接转矩控制系统的效率最优控制[J].电工技术学报,2013,28(4):255-260.

Zhang Xinghua,Sun Zhenxing,Wang Deming.Optimal efficiency control of direct torque controlled induction motor drives for electric vehicles[J].Transactions of China Electrotechnical Society,2013,28(4):255-260.

[5] Bazanella A S,Reginatto R.Robustness margines for indirect field-oriented control of induction motors[J].IEEE Transactions on Automatic Control,2000,45(6):1226-1231.

[6] 陈振锋,钟彦儒,李洁,等.基于改进磁链观测器的感应电机转速辨识[J].电工技术学报,2012,27(4):42-47.

Chen Zhenfeng,Zhong Yanru,Li Jie,et al.Speed identification for induction motor based on improved flux observer[J].Transactions of China Electrotechnical Society,2012,27(4):42-47.

[7] 尹忠刚,刘静,钟彦儒,等.基于双参数模型参考自适应的感应电机无速度传感器矢量控制低速性能[J].电工技术学报,2012,27(7):124-130.

Yin Zhonggang,Liu Jing,Zhong Yanru,et al.Low- speed performance for induction motor sensorless vector control based on two-parameter model reference adaptation[J].Transactions of China Electrotechnical Society,2012,27(7):124-130.

[8] 邓歆.异步电机全阶磁链观测器的分析、设计及其应用研究[D].武汉:华中科技大学,2010.

[9] 张永昌,赵争鸣,张颖超,等.基于全阶观测器的三电平逆变器异步电机无速度传感器矢量控制系统[J].电工技术学报,2008,23(11):34-40.

Zhang Yongchang,Zhao Zhengming,Zhang Yingchao,et al.Sensorless vector control system of induction motor fed by three-level inverter using a full order observer[J].Transactions of China Electrotechnical Society,2008,23(11):34-40.

[10] Hinkkanen M.Analysis and design of full-order flux observers for sensorless induction motors[J].IEEE Transations on Industrial Electronics,2004,51(5):1033-1040.

[11] Kim J H,Woo J,Ki S.Novel rotor-flux observer using observer characteristic function in complex vector space for field-oriented induction motor drives[J].IEEE Transaction on Industry Applications,2002,38(5):1334-1343.

[12] Kubota H,Matsuse K.New adaptive flux observer of induction motor for wide speed range motor drives[C].IEEE IECON'90,1990:921-922.

[13] Maes J,Melkebeek J A.Speed sensorless direct torque control of induction motors using an adaptive flux observer[J].IEEE Transactions on Industry Applications,2000,36(4):778-785.

[14] Vicente I,Endemano A,Garin X,et al.Adaptive full order observer based stable speed sensorless scheme for vector controlled induction motor drives[C].EPE'09,2009:1-10.

[15] Kubota H,Matsuse K,Hori Y.Behavior of sensorless induction motor drives in regenerating mode[C].Proceedings of Power Conversion Conference,Nagaoka,1997,2:549-552.

[16] Suwankawin S,Sangwongwanich S.A speed-sensorless IM drive with decoupling control and stability analysis of speed estimation[J].IEEE Transations on Industrial Electronics,2002,49(2):444-455.

[17] Suwankawin S,Sangwongwanich S.Design strategy of an adaptive full-order observer for speed-sensorless induction-motor drives-tracking performance and stabilization[J].IEEE Transations on Industrial Electronics,2006,53(1):96-119.

[18] Harnefors L,Hinkkanen M.Complete stability of reduced-order and full-order observers for sensorless IM drives[J].IEEE Transations on Industrial Electronics,2008,55(3):1319-1329.

[19] Kubota H,Matsuse K,Nakano T.DSP-based speed adaptive flux observer of induction motor[J].IEEE Transactions on Industry Applications,1993,29(2):344-348.

[20] Yang G,Chin T H.Adaptive-speed identification scheme for a vector-controlled speed sensorless inverter- induction motor drive[J].IEEE Transactions on Industry Applications,1993,29(4):820-825.

[21] Rashed M,Stronach F,Vas P.A new stable MRAS- based speed and stator resistance estimators for sensorless vector control induction motor drives at low speeds[C].38th IAS Annual Meeting,2003,2:1181-1188.

[22] Kubota H,Matsuse K.Speed sensorless field-oriented control of induction motor with rotor resistance adapta- tion[J].IEEE Transactions on Industry Applications,1994,30(5):1219-1224.

[23] Harnefors L.Design and analysis of general rotor flux oriented vector control systems[J].IEEE Transactions on Industrial Electronics,2001,48(2):383-390.