非均匀内流对航空燃油管道振动特性影响的波动法研究

王良伟

（中国特种飞行器研究所，湖北 荆门 448035）

0 引言

输流管道的流致振动问题普遍存在于众多的工程领域中。在很多发达国家，每年因管道振动造成的损失都接近100亿美元［1］。管道的流致振动问题困扰着工业领域的工程师和研究者，解决管道系统流致振动问题的关键是获取能够准确描述输流管道系统流致振动规律的动力学模型［2］。事实上，在输流管道动力学的研究中，非均匀流和均匀流模型的本质区别在于其速度沿截面的分布不同。在目前已有的输流管道研究中，大部分研究者采用的是活塞流模型［3］，即认为截面上的流速是均匀分布的。活塞流模型有一定的合理性，但是在理论上并不精确，由于管壁和流体之间摩擦力的存在，输流管道中同一个截面上流体速度并不是处处相等的。根据流体力学相关理论，其内流场的分布与管内流体的雷诺数直接相关［4］。当流体的雷诺数超过临界值时，管中流体形式为湍流，由于湍流的流速沿截面的分布是近似均匀的，因此可以用活塞流模型来描述。但是当流体的雷诺数尚未超过临界值时，管中输送的流体以层流形式存在，此时，流速沿横截面的分布呈抛物面形［4］。

目前，研究者已经对于管内输送层流和湍流的情况进行了初步的研究，针对已有的输流管道动力学方程没有考虑流体流动的非均匀性，C.Q.Guo［5］等对于输送层流和湍流时管道的动力学方程进行了一定的修正，这种修正在已有的输流管道动力学方程中的离心力项增添了一个表征流体非均匀性的参数。A.M.Helluma［6］等采用NPLUG模型来表征非均匀流场，即认为非均匀流场是由多层均匀流组合而成。

在求解输流管道动力学方程的方法中，波传播解法是一种新型的半解析方法，通过弹性波在介质中的循环传播以及在介质边界处的反射与透射过程来建立控制方程，从而求解系统的动力学特性。B.H.Li等利用波动方法求解过输流多跨直管道和弯曲管道自由振动的动力学响应［7-8］。波传播解法易于编程实现，并有较高的计算效率。

本文采用开放系统Hamilton原理直接建立输送层流时航空燃油管道的动力学控制方程，并利用波传播解法对于控制方程进行求解，得到管道的前四阶固有频率，并将输送均匀流和非均匀流时管道的固有频率进行了对比，为非均匀流对管道的动力学特性的研究提供了一定的借鉴。

1 非均匀流管道动力学模型

含有非均匀流的管道如图1所示，假定管内流体处于层流状态。

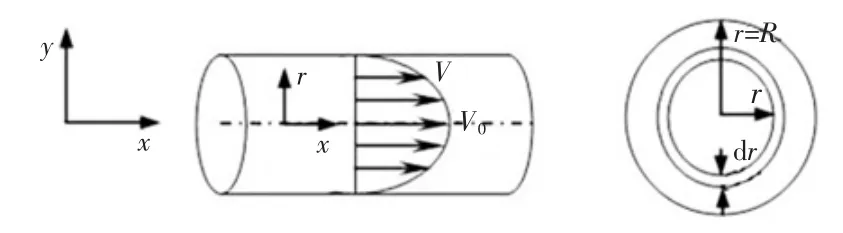
图1 含非均匀流的管道示意图

对于层流来说，截面上流速的分布呈抛物面型，流速方程为

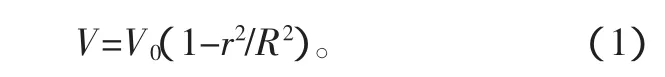
式中：r为管道横截面的径向坐标；2R为管道的内径；V为管流流速，V0为管道中心处的流体流速。

本文所研究的管道是细长管，因此采用Euler-Bernoulli梁模型，假设管道两端简支，其横向振动位移简图如图 2 所示［9］。

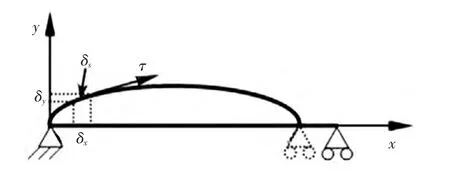
图2 简支管道横向振动示意图

采用Hamilton原理进行输流管道动力学模型的建立，输流管道系统是一个开放系统，开放系统的Hamilton原理具有以下形式：

式中∶￡为系统的拉格朗日函数，即系统的动能函数与势能函数之差；δW为非保守力做功；M为单位长度流体质量；re为管道流体出口端的位置矢量。

经过推导得到输送层流时的管道动力学方程为

通过式（3）和式（4）的对比，发现采用非均匀流模型建模时，动力学方程中的离心力项，以及科氏力项 MV与采用均匀流模型时的动力学方程中的对应项有所区别。而对于非均匀流和均匀流来说，动力学方程中的弯矩项以及加速度项（m+M）是相同的。

事实上，非均匀流和均匀流模型的本质区别在于其速度沿截面的分布不同，因此，在动力学方程中，涉及流速分布的项是不同的，而不涉及流速分布的项是相同的。因此，对于比较简单的非均匀流场，可以直接采用较少的参数对于均匀流情况下输流管道动力学方程中流速项进行修正，即得到非均匀流情况下输流管道的动力学方程。

2 非均匀流管道的波传播解法

输流管道的横向振动可以看作是简谐振动的叠加，简谐振动方程为

式中：k为波数；ω为圆频率；c为常数。

将式（7）代入式（3）中，可以得到原偏微分方程的特征方程：

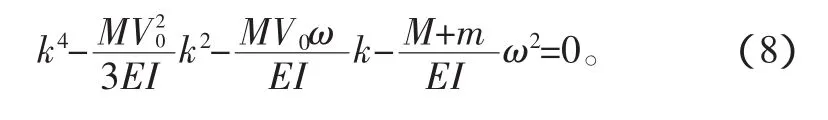
式（8）中k有4个根，4种不同的波数分别对应4种波模式。管道的位移形式可以写为

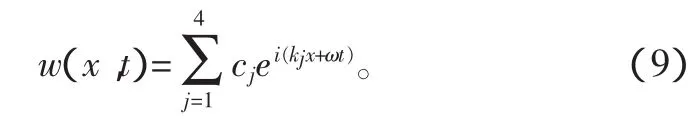
为表示方便，以下标1、2代表左行波，3、4代表右行波。简支管道中的波传播如图3所示。

图3 简支管道中的波模式

图（3）中所示 l、r分别表示左右两端部，上标+、-分别表示向正、负方向传播的波。波的具体形式为∶

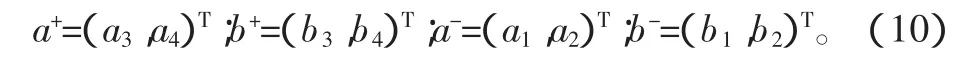
依据波的循环传播原理［10］，弹性波在管道中传播，并且在管道端部发生反射，其传播矩阵和反射矩阵分别为TR，TL，Rr，Rl波的循环传播关系为：

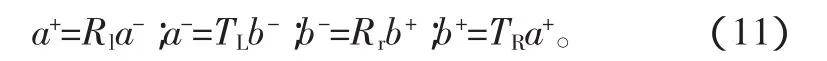
根据管道两端简支的边界条件，可以得到在边界处的反射矩阵为

上述方程有非零解的条件是

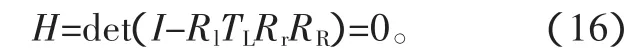
通过求解式（16）可以得到输流管道系统的固有频率。

由于在求解过程中，一部分数值计算可以用较为简单的理论计算所替代，因此波传播解法的计算效率较高［8］，此外，波传播解法作为一种半解析的方法，在计算过程中用波动函数作为形函数，因此波传播解法的计算精度较高。

3 算例及分析

以图4所示的输油管道为例进行分析，系统几何尺寸如图4。

图4 管道尺寸示意图

3.1 均匀流输液管道的固有频率

在对方程（16）进行求解时，直接寻找H实部和虚部同时为零的点存在困难，因此对于H的模进行取对数运算，并且作“频率-ln|H|”曲线，曲线上斜率为负无穷的点（即图中的尖点）即近似认为是固有频率点。

假设管道内流为均匀流，利用波传播解法计算流速分别为7.5 m/s、15 m/s和22.5 m/s时其固有频率，结果如图5所示。图5中每个斜率接近负无穷的点对应的横坐标即是输流管道的固有频率点。可以看出，管道内流为均匀流时，输液管道的各阶固有频率随流速的增加而减小。

3.2 非均匀流输液管道的固有频率

假设管道内流为非均匀流，截面上流速的分布呈抛物面型，利用波传播解法计算截面最大流速分别为15 m/s、30 m/s和45 m/s时的固有频率，结果如图6所示。图6中每个斜率接近负无穷的点对应的横坐标即是输流管道的固有频率点。可以看出，管道内流为非均匀流时，随着流速的增加，其各阶固有频率也会减小，这和均匀流的计算结果是一致的。事实上，随着流速的增加，两端简支管道的刚度会有一定的降低，当流速增加至足够大时，输流管道将会发生失稳。

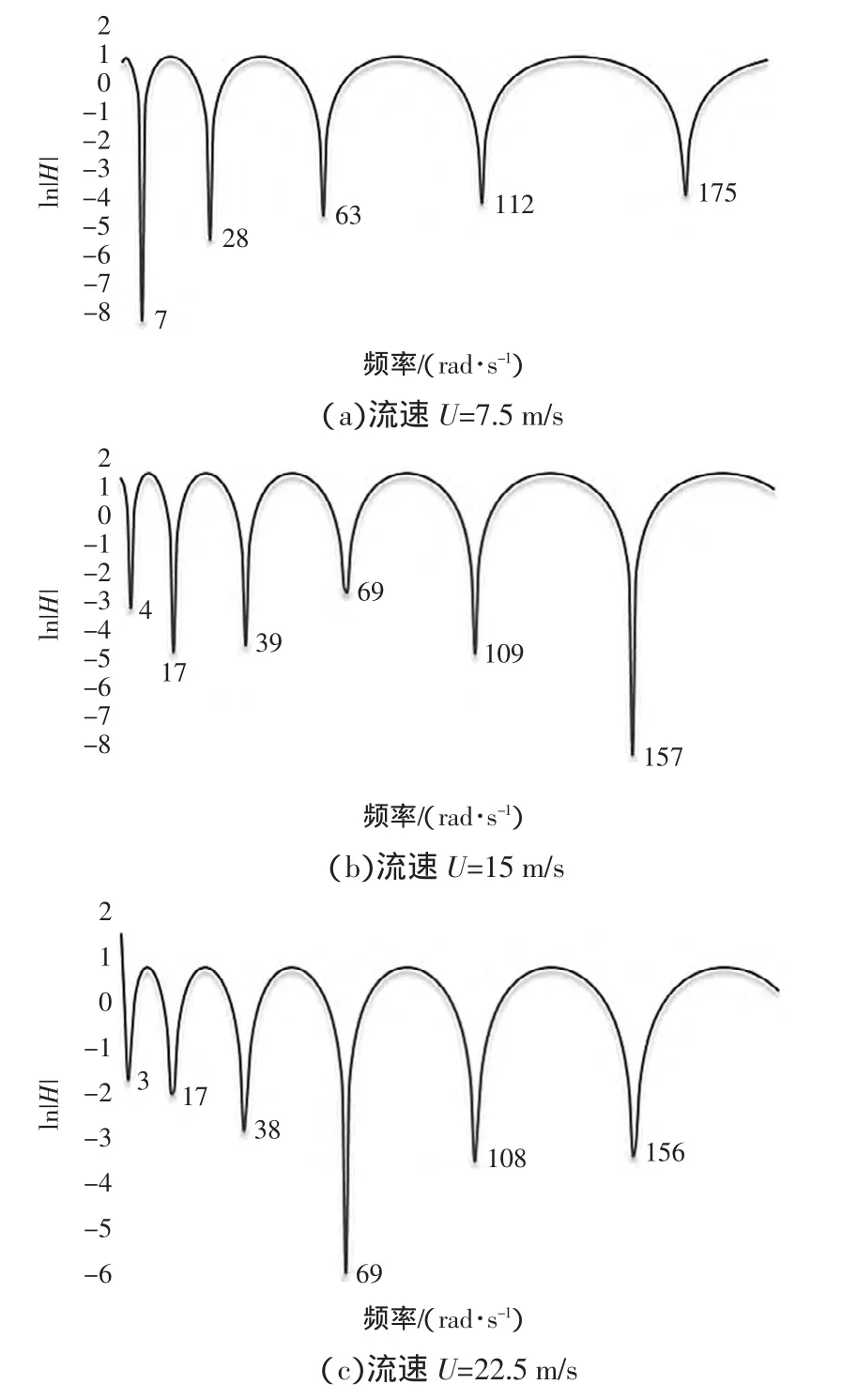
图5 管道输送均匀流时固有频率计算结果

3.3 结果讨论与分析

将管道输送均匀流和非均匀流时的计算结果进行对比如表1。

从表1中可以看出，在同样的有效均流速下，输送层流时管道的固有频率高于输送均匀流时的固有频率。这看起来似乎不合常理，因为层流是非均匀流，输送层流的管道似乎应当有更小的固有频率，事实上，均匀流是充分发展的湍流，而层流是雷诺数不超过临界值的稳定流，输送层流的管道应当有更大的刚度。

另一方面，从两种情况下的动力学方程的对比中（式（4）、式（5））可以看出，非均匀流影响到的是方程的离心力项，非均匀流使离心力项相比于均匀流来说有所增大，这使输流管道的固有频率有所降低，而从振动的角度来说，非均匀流使整个系统的刚度增大了，前者的效果被后者抵消掉，因此整体上来说，固有频率会有所提高。

对于更高的流速的层流，本文不作计算，因为流体的雷诺数正比于流速，随着流速的增加，流体雷诺数达到临界值，层流不复存在，而转捩成湍流。

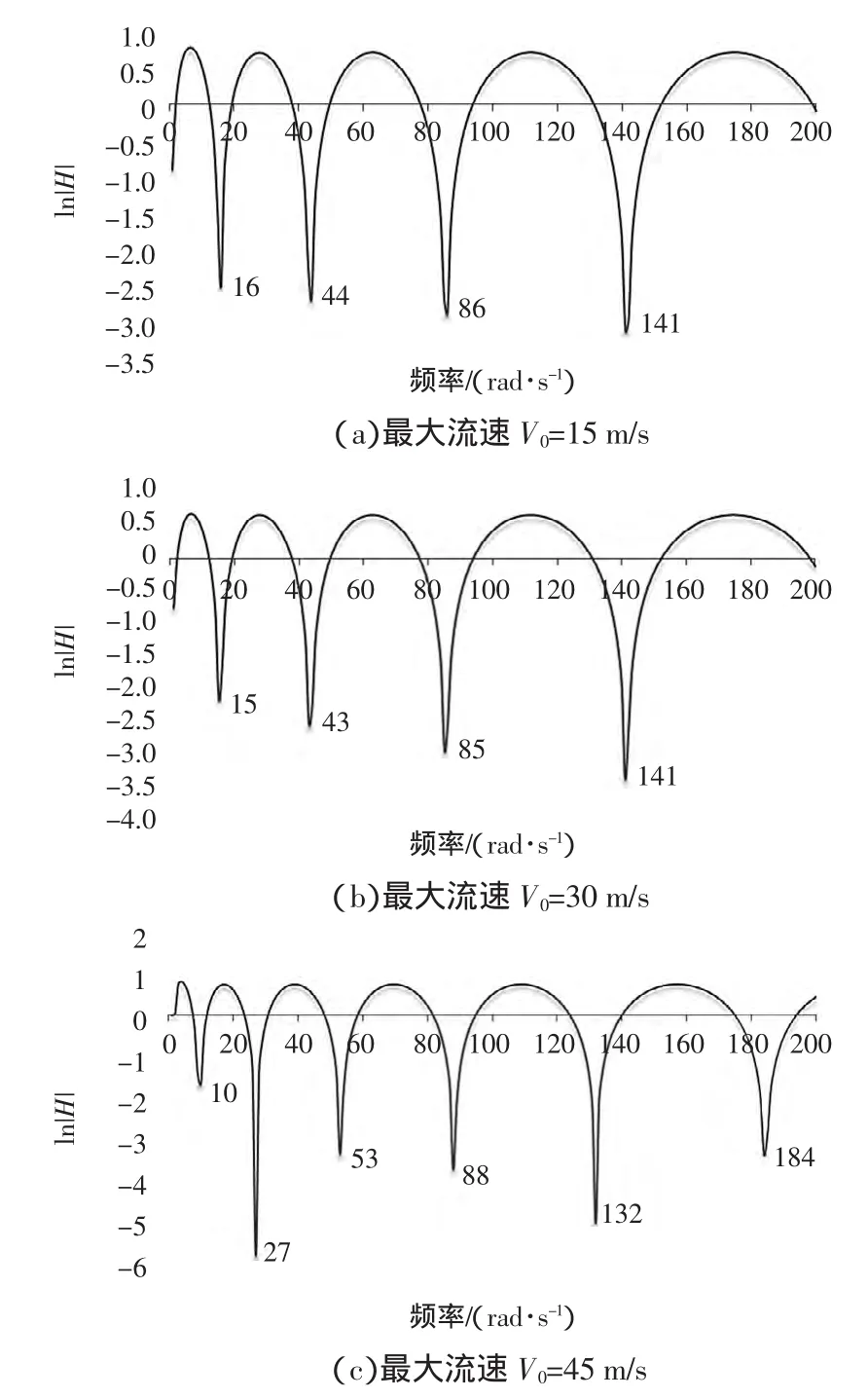
图6 管道输送层流时固有频率计算结果

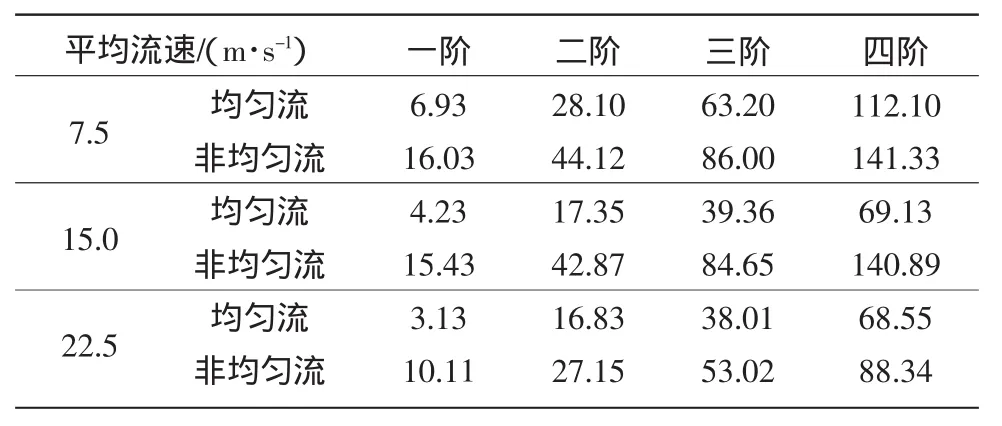
表1 管道输送均匀流和非均匀流时的前四阶固有频率 rad/s

4 结 论

应用开放系统的Hamilton原理推导了非均匀流输液管道的动力学控制方程，利用波传播解法求解了输流管道系统的固有频率，并与均匀流时的计算结果进行对比，得到以下结论∶1）无论对于非均匀流还是均匀流，输流管道的固有频率随内流流速的增加而减小。2）非均匀流输流管道相比于均匀流输流管道有较高的固有频率，这是由于非均匀流时，输流管道的刚度有所增大导致的。

［1］ 李公法，孔建益，幸福堂，等.考虑固液耦合的充液管道系统振动能量流研究［J］.湖北工业大学学报，2005，20（3）：74-77.

［2］ Paidoussis M P.The canonical problem of the fluid-conveying pipe and radiation of the knowledge gained to other dynamics problems across Applied Mechanics［J］.Journal of Sound and Vibration，2008（3）：462-492.

［3］ Paidoussis M P.Fluid-structure interactions ［M］.London∶Academic Press Limited，1998.

［4］ 张也影.流体力学［M］.2版.北京：高等教育出版社，1998：286-288.

［5］ Guo CQ，Zhanga CH，Paidoussis M P.Modification of equation of motion of fluid-conveying pipe for laminar and turbulent flow profiles［J］.Journal of Fluids and Structures，2010，26（5）∶793-803.

［6］ Helluma A M，Mukherjeea R，Hullb A J.Dynamics of pipes conveying fluid with non-uniform turbulent and laminar velocity profiles［J］.Journal of Fluids and Structures，2010，26（5）∶804-813.

［7］ Li Baohui，Gao Hangshan，Zhai Hongbo，et al.Free vibration analysis of multi-span pipe conveying fluid with dynamic stiffness method ［J］.Nuclear Engineering and Design，2011，241（3）∶666-671.

［8］ 李宝辉，高行山，刘永寿，等.输液曲管平面内振动的波动方法研究［J］.固体力学学报，2012，33（3）：302-308.

［9］ Li Baohui，Gao Hangshan，Liu Yongshou，et al.Transient response analysis of multi-span pipe conveying fluid［J］.Journal of Vibration and Control，2013，19（14）：2164-2176.

［10］ Tan C A，Kang B.Free vibration of axially loaded，rotating Timoshenko shaft systems by the wave-train closure principle［J］.International Journal of Solids and Structures，1999，36（26）∶4031-4049.

（编辑昊 天）