基于有限元的过盈配合平均接触压力求解

沈健， 朱亚军， 周丹， 刘光复， 杜晓东

（合肥工业大学，合肥230009）

0 引言

过盈配合是一种常见的连接方式，具有结构紧凑、对中性好、承载能力大、耐冲击性好等优点。工程中通常按照弹性力学厚壁圆筒理论进行设计计算，理论计算时忽略了轴向应力，只考虑法向应力和周向应力，法向应力即接触压力。

过盈配合构件工作时，依靠过盈量产生的接触压力传递扭矩和轴向力，传递扭矩很大时设计的过盈量就需要很大，接触压力也相应很大。由于一些场合下过盈配合需要拆解，在应用上认为拆解时所需的拆解力是由于接触压力和摩擦因数导致的，且是线性关系，因此得到平均接触压力就可以得到宏观拆解力。有限单元法能很好地解决过盈配合接触的计算问题，并可以求解各种耦合问题，为实际问题的求解提供了有效的方法。

1 采用有限单元法计算过盈配合平均接触压力

1.1 过盈配合接触问题的有限元求解方法

过盈配合是一种典型的非线性接触行为，接触问题的算法有罚函数法、拉格朗日法、增强拉格朗日法。罚函数法是计算每一载荷子步时,先检查接触面和目标面是否有穿透，若有穿透则在接触面间引入法向接触应力，其值大小与接触刚度和穿透深度成正比。拉格朗日法是把接触力作为一个独立的自由度，可以实现穿透为零的真实接触条件。但由于自由度增加会降低计算效率，增强拉格朗日法是不断更新接触刚度的罚函数，直到计算的穿透值小于允许值为止，该算法总体刚度矩阵较少出现病态，接触单元接触刚度取值更合理。本文采用增强拉格朗日法进行求解。

1.2 有限单元法的设置和求解

根据以上接触问题计算方法的原理，建立三维模型导入有限元软件Workbench中，仿真计算基于静力模块进行，设置接触为摩擦接触，添加摩擦因数，有限元模型的过盈量通过接触单元实常数过盈的方法进行设置，以输入offset（偏移量）的值来实现，设置固定约束面。设置时为了方便单元应力的提取，手动设置内孔面为接触面（contact174），轴表面为目标面。

经过有限元计算可以得到各单元受力情况和受力单元数目，当接触单元都受力时，平均接触压力是所有接触单元的接触压力值的平均值。当受力单元数小于接触面单元数时，采用将各受力单元面积乘以各单元接触压力再求和得到总接触力，总接触力除以接触面的总面积得到平均接触压力。以下用实例来说明该计算过程。

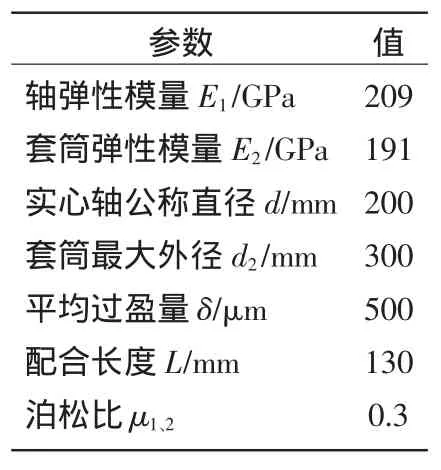
表1 轴和套筒的参数

2 计算实例

2.1 轴和套筒过盈配合平均接触压力的计算

给定轴和套筒的过盈配合模型如图1所示，其各项参数如表1所示，设摩擦因数为0.1，过盈量为0.5 mm，添加图1所示固定约束，对轴和叶轮装配体进行自由网格划分，设置轴和叶轮网格尺寸为15 mm，接触面单元的网格大小为5 mm，设置内孔面为接触面（contact174）。对模型求解，得到896个接触单元都受法向应力，直接对各接触单元的法向应力求平均值即可得到平均接触压力，为132.2 MPa。

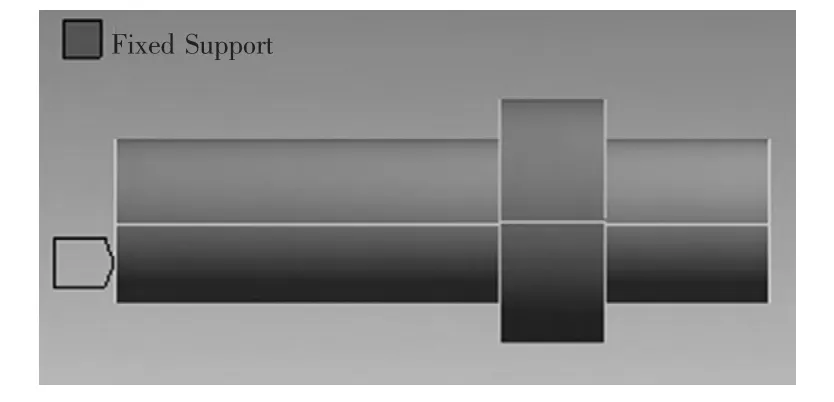
图1 轴和套筒约束模型

计算过盈配合接触压力的理论公式［4］为

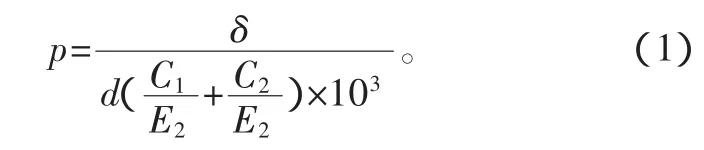
式中：C1为轴的刚性系数为套筒的刚性系数为平均过盈量，μm，d 为轴孔的公称直径mm；d1为空心轴内孔径，实心轴为0。

该公式以理想状态的轴和套筒配合为基础。将表1中的参数带入式（1）可以求得接触面间的接触压力为135 MPa。比较有限元计算结果和式（1）的计算结果，相对误差为2.2%，因此上述有限单元法求解的平均接触压力与理论计算结果相吻合。由此可见，有限单元法能很好地解决过盈配合的计算问题。

对于工程中大量复杂结构的过盈配合问题（如轴和叶轮），已没有相应的理论计算公式，但采用上述的有限元方法的计算结果是可信的。

2.2 存在形状误差的轴和叶轮过盈配合平均接触压力的计算

2.2.1 轴的弯曲几何模型建立

大型离心压缩机的轴和叶轮通过大过盈配合（如φ225H7/y6）来传递扭矩，叶轮结构复杂，其基本参数如表2所示。

表2 叶轮的基本参数

轴在整个生产、服役周期内，容易产生弯曲，在叶轮需要修复时，要对叶轮进行加热拆解处理，因此需要对拆解过程的接触情况进行分析。为研究方便，将轴存在弯曲时配合模型简化成如图2所示，将配合面中部的弯曲量设为最大，用轴线的直线度来反映其弯曲程度，设直线度误差为0.05 mm。

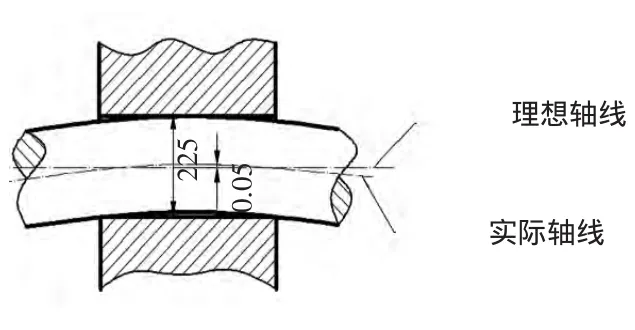
图2 轴弯曲时的配合模型

2.2.2 有限单元法求解的设置

计算接触压力时的相关材料属性、接触和网格划分的设置与上述轴和套筒的模型相同，将图3中X轴负方向的端面添加面固定约束，得到接触面（contact174）单元个数约为7700个。两个配合面之间的接触压力来源于设置的过盈量和轴的直线度误差形成的实际过盈量。

图3 轴和叶轮有限元网格划分

模拟加热拆解过程，采用瞬态热-结构耦合进行计算，添加材料的热力学性能参数（见表3），实际加热方式为流道面加热，温度载荷350℃，加热时间为1 000 s。

2.2.3 有限单元法计算结果分析

通过有限元计算得到以下情况的接触压力分布云图，如图4～图7所示。

表3 轴和叶轮的热力学性能参数

图4 不受热、轴无直线度误差时的接触压力云图

图5 不受热、轴的直线度误差为0.05 mm时的接触压力云图

图6 受热、轴无直线度误差时接触压力云图

图7 受热、轴的直线度误差为0.05 mm时的接触压力云图

对比图4和图5，可以得到接触压力直观的分布情况，接触压力最大的区域为中间部位，这是由于中间区域叶轮刚度最大导致的；当轴的直线度误差为0.05 mm时，会严重影响叶轮上的接触压力分布状况，接触压力最大的区域会向实际过盈量最大的部位移动；轴的直线度误差为0.05 mm时的最大接触压力大于无直线度误差状态下的最大接触压力。

对比图4和图6，受热时接触压力的分布相对于不受热时变化很大，配合面靠叶轮进气口处（配合面最右端）的接触压力最大。图6、图7所示中心区域接触压力很小，图7中部分接触区域接触压力几乎为0。

针对得到的计算结果图4和图5，采用ANSYS后处理技术，提取接触单元的接触压力，应用MATLAB编程连成曲面，建立表面接触压力分布曲面如图8和图9所示。设定该曲面的3个坐标分别为配合面轴向尺寸、圆周方向偏转角度、接触压力的数值。

由图8、图9可知：1）轴无直线度误差时，过盈配合接触压力的分布随着轴向尺寸的变化而变化，接触压力的最大值出现在图4所示叶轮距离左端面42 mm处，接触压力沿圆周方向的变化不大；2）轴的直线度误差为0.05mm时，应力分布发生变化，应力随轴向位置和偏转角度的不同变化较大。最大接触压力出现在图5所示叶轮距离左端面42 mm处，周向偏转角度为0°。

图8 轴无直线度误差的接触压力曲面

图9 轴的直线度误差为0.05 mm时的接触压力曲面

分别建立存在不同的直线度误差的轴和叶轮装配的有限元模型，经求解得到轴和叶轮装配体的最大接触压力和平均接触压力的变化情况。

由图10可知，最大接触压力随轴弯曲程度的增大而增大，加热时最大接触压力会减小，这是由于加热降低了实际过盈量。

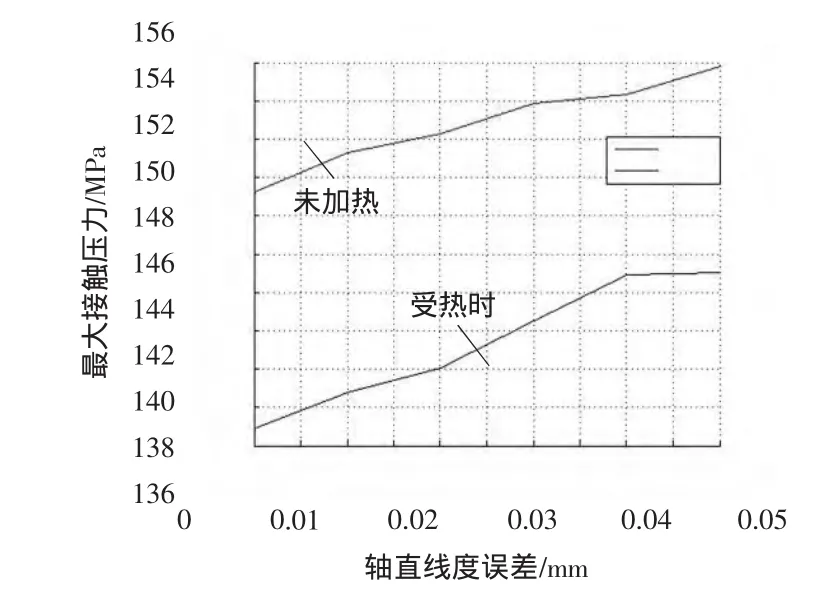
图10 轴直线度误差与最大接触压力的关系

由图11可知，两表面之间的平均接触压力随轴的直线度误差的增大变化很小。这是由于轴虽然存在直线度误差，导致各处的接触压力分布发生变化，造成局部接触压力增大，但其他区域的接触压力会减小，而总的接触压力不会有较大的变化，因此使平均接触压力和拆解力不会随误差增大发生较大变化。这里也有可能研究的直线度误差过小，且网格尺寸较大，导致平均接触压力变化不明显。通过计算，得到轴和叶轮配合未加热时，平均接触压力为115 MPa左右。加热时降低到55 MPa左右。加热时平均接触压力降低了约52%，因此拆解力也有相同的降幅。

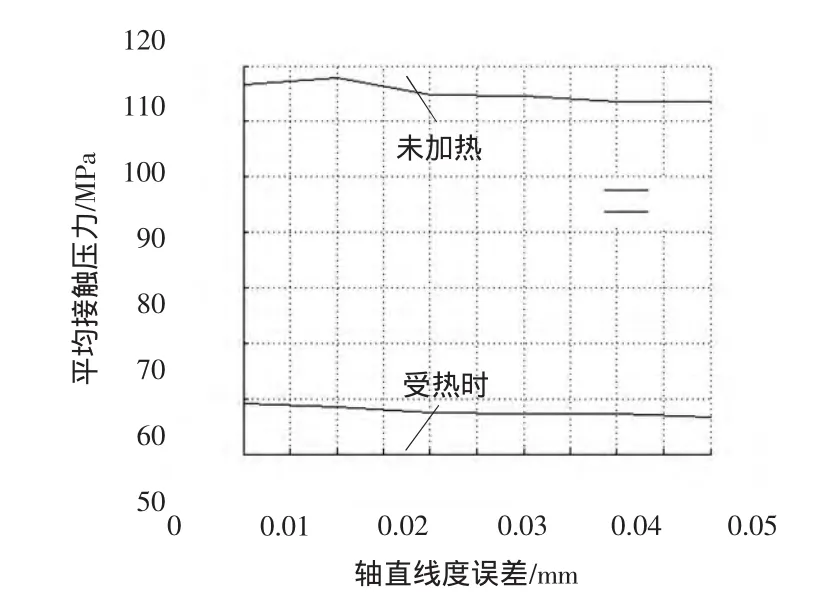
图11 轴直线度误差与平均接触压力的关系

3 结论

1）使用有限单元法求得了过盈配合的平均接触压力。

2）轴存在直线度误差时，对过盈配合件的两接触表面的接触压力分布会有较大的影响。最大接触压力随着轴直线度误差增大而增大，平均接触压力和拆解力变化不大。

3）对叶轮加热时，过盈配合的平均接触压力会有大幅度的降低，采用有限元方法求得变化规律。

［1］ 高俊福.大型离心压缩机轴热装弯曲机理研究［D］ .大连：大连理工大学，2013.

［2］ 高耀东，张玉宝.ANSYS机械工程应用精华60例［M］.北京：电子工业出版社，2012.

［3］ Bengeri M,Mack W.Theinfluenceof thetemperaturedependence of the yield stress on the stress distribution in a thermally assembled elastic-plastic shrink fit［J］.ACTA MECHANICA,1994，103（1-4）：243-257.

［4］ 濮良贵，纪名刚.机械设计［M］.8版.北京：高等教育出版社,2005.

［5］ 李桂华.复杂规则曲面机械零件的热变形理论及应用研究［D］.合肥：合肥工业大学，2006.