一种新型回转平动传动结构设计及优化仿真分析
娄唯佳, 张志强, 黄民
(北京信息科技大学,北京 100192)
0 引言
通过对链传动机构和齿轮传动机构的组合,形成一种新型的回转平动传动结构,其可作为一种竖直旋转回转库的主体结构。
该结构充分利用空间,实现了很高的存储比例(实际存储面积与设备占地面积之比)[1]。而且密闭的存储空间可以有效地避免灰尘和阳光的侵害。通过电气控制系统和顶层管理系统的管理,使整个传动结构实现了全自动的运转,降低了劳动强度。该结构适应性强,但由于链传动速度的限制,其运转速度不宜过快。另外,该结构为非对称性传动结构,因此需要高等级的安装精度。
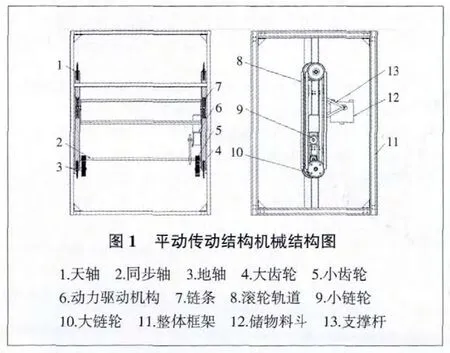
1 平动传动结构的工作原理
如图1所示,回转平动传动结构主要由以下部分组成[2-4]。
整个机构由整体框架11支撑,包括机构外壳、传动结构支撑架和整体机构底座。传动结构支撑架主要起到支撑同步轴、天轴与地轴的作用,通过螺栓连接与整体机构底座相连。机构外壳由4根外壳支撑立柱和四周面板组成,主要起覆盖作用。
平动传动通过天轴1、同步轴2、地轴3及这些轴上的传动机构实现,其中地轴和天轴均为两根,同步轴一根。同步轴将运动传递给两侧的地轴,实现两侧地轴运动的同步,地轴再将运动传递给天轴,从而实现平动运动。地轴是下传动主动轴,天轴为上传动被动轴。地轴一端与传动大链轮10配合,另一端与大齿轮4配合。同步轴2为转轴,主要用于同步左右两个链传动。同步轴两端分别安装小齿轮5,两齿轮中间偏右安装小链轮。小齿轮与地轴上的大齿轮啮合,将运动和动力传递给地轴。小链轮与动力驱动机构6中的小链轮9构成一级链传动,将动力驱动机构的运动与动力传递给同步轴。其中动力驱动机构由电动机和一级链传动组成。
储物料斗的两侧非对称安装支撑杆13。支撑杆的一端通过铰接与链条联接,另一端通过弯轴与做平动运动的储物料斗的一侧联接,从而使储物料斗随着链条的运动做竖直运动和回转运动。储物料斗两侧与支撑杆的连接点在同一个水平面上,但并不对称。这样可以防止储物料斗翻转。
智能控制系统包含上位计算机、欧姆龙PLC、光电传感器、电气控制柜和其他安全检测装置。上位计算机通过串口RS232与欧姆龙PLC通信,从而实现整个机构的智能控制,保证储物料斗快速、准确地运转到指定位置。
动力驱动机构中的异步电动机提供回转平动传动机构运转时的动力,通过减速链传动带动同步轴转动。同步轴上的两个小齿轮与两侧地轴上的大齿轮啮合,并带动地轴转动,地轴上的大链轮与天轴上的大链轮实现传速比为1∶1的链传动,从而驱动大链轮转动。大链轮带动链条,链条通过支撑杆牵引储物料斗做循环的竖直和回转运动。储物料斗中存放物料,当接收到控制指令后,整个机构按最短路径自动运转,快速而准确地将物料送达存取口。
2 最小占用空间布局优化设计
当减速链传动、齿轮传动和储物料斗设计完成后,水平方向两侧链轮的距离和储物料斗的高度H及宽度W已确定。最小占用空间主要由储物料斗运动平面内水平占用空间决定,即由两侧等速链传动机构决定,因此要针对此链传动进行结构优化设计。由于占用空间受储物料斗运动的影响,因此储物料斗相对链条的位置会影响链传动的设计。另外大链轮的节圆半径也影响储物料斗的回转半径。
根据设计经验选定链条节距p和大链轮节圆半径r,设储物料斗相对链条的距离为c。当有最小的储物料斗回转半径时,保持其它结构尺寸不变,获得整个钢结构的最小框架宽度,从而使整个结构的占地面积最小。
2.1 设计变量及目标函数
图 为传动系统及储物料斗示意图。设储物料斗高度H、宽为W、链条的节距为p、箱斗间的竖直距离为Δc、支撑架的长度为l。从图中可以看出,前后两侧的料斗运动情况是相同的,因此以下只对单侧进行分析。
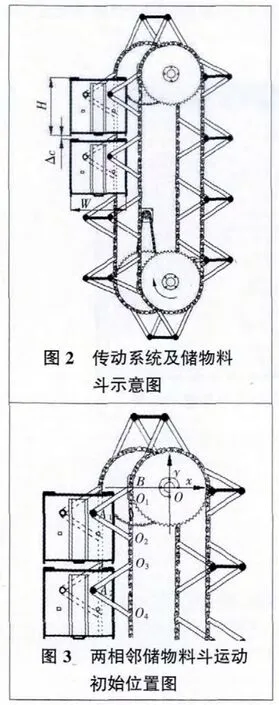
首先建立参考坐标系,如图3所示。以前侧从动链轮中心O为原点,O1为储物料斗1的支撑杆1与传动链条连接点,O2为储物料斗1的支撑杆2与传动链条连接点,O3为储物料斗2的支撑杆3与传动链条连接点,O4为储物料斗2的支撑杆4与传动链条连接点。A1、A2分别为储物料斗1、储物料斗2与对应的两个支撑杆的连接点[5]。设链轮顺时针旋转。
如图3,假设B点为前侧从动大链轮节圆上的一点。设θ0为O1、O2两点同时沿圆弧旋转时连线OO1和OO2之间的夹角,有 θ0小于 90°,θ1为 B 点的旋转角度,θ2为 O2、O3两点同时沿圆弧旋转时连线OO2和OO3之间的夹角[5]。
分析可知,存在一个独立变量θ1。储物料斗竖直运动时,储物料斗相对链条的距离c为支撑杆在x轴上的投影;储物料斗回转运动时,储物料斗相对链条的距离c为A1或A2到原点O的距离与链轮节圆半径r之差。另外为了确保整个回转结构拥有最小宽度,储物料斗回转半径应最小。故目标函数取为储物料斗回转半径L,即储物料斗相对链条的距离c和链轮节圆半径r之和。同时引入系数 λ,令 c=λr,可以确定
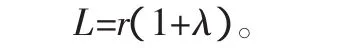
根据上式建立数学函数,确定目标函数的表达式为
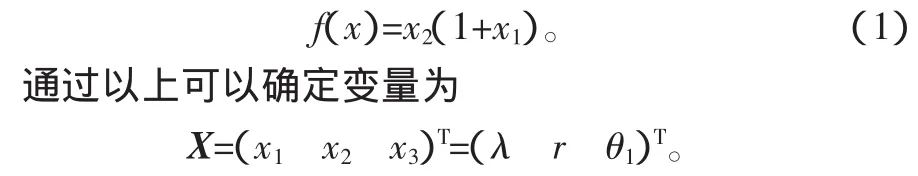
2.2 约束条件
1)确保左右两侧储物料斗竖直运动不干涉。此时料斗回转直径2L,必须大于料斗宽度W,已设储物料斗宽度W为325 mm,由L=r(1+λ)可知:
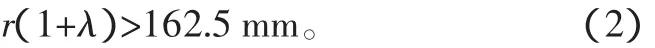
2)当储物料斗相对链条的距离c过大时,在竖直运动过程中链条会受到很大的水平作用力,并影响竖直运动;当储物料斗相对链条的距离c过小时,左右两侧储物料斗在运动中可能会干涉。综合考虑,取150 mm≤c≤280 mm,即
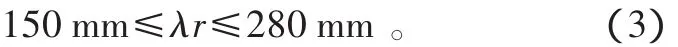
3)选取与大链轮啮合的输送链条的节距p,取p=19.05 mm;选取大链轮齿数z为30~50。根据大链轮分度圆计算公式 d=p/sin(180°/z),可得
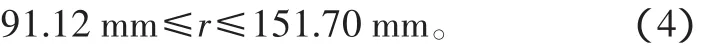
4)为了保证竖直运动时相邻的两相邻储物料斗不发生干涉现象,两相邻储物料斗支撑弯轴中心距离h必须满足以下条件∶h≥H+Δc
式中储物料斗高度H=358 mm已知,且有Δc≥3 mm。根据链传动特点可知h=np(n为相邻两储物料斗上或下支撑杆之间的链节数)。综上可求得n>18,选n=19,即两侧链传动中的链条链节数分别为190。故有h=361.95 mm。
5)θ0、θ2分别为
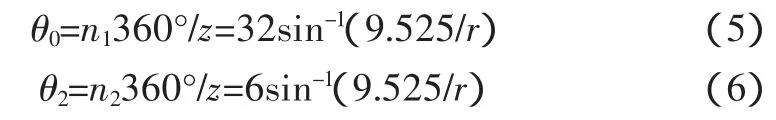
式中:n1为与储物料斗1连接的两个支撑杆之间的链节数量;n2为储物料斗1的下支撑杆与储物料斗2的上支撑杆之间的链节数量。
2.3 数学模型
综上所述,将变量 x1、x2和 x3代入式(2)~式(4),则基于最小占用空间思想链传动优化数学模型表达为
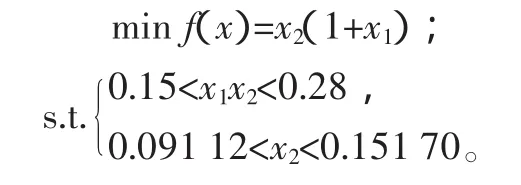
当一个储物料斗的一个支撑杆与链条的连接点进入圆弧运动,而另一个连接点及后面或上面的储物料斗还在进行竖直运动时,有0≤θ1≤θ0,此时的第三约束方程为x2(1+x1)-x1x3<156.35。
当一个储物料斗的两个支撑杆与链条的连接点进入圆弧运动,而另一储物料斗还在进行竖直运动时,有θ0<θ1≤θ0+θ2,此时的第三约束方程为 x1x3-x2cos(x3-θ0/2)<156.35。
当一个储物料斗的两个支撑杆与链条的连接点进入圆弧运动,而另一储物料斗的一个支撑杆与链条的连接点进入圆弧运动,而另一个连接点还在进行竖直运动时,有θ0+θ2<θ1≤π 此时的第三约束方程为 x2/cos(x3-θ0/2)>358。
当两个储物料斗均有一个支撑杆与链条的连接点进入圆弧运动,而另一个连接点还在进行竖直运动时,有π<θ1≤[θ0+(θ2+π)/2],此时的第三约束方程为x2(1+x1)x3>358。
2.4 优化求解
可以看出,上述数学模型为有约束非线性优化问题。因此可通过MATLAB中的fmincon[6]函数求解。
编写MATLAB目标函数文件,在命令窗口调用fmincon函数并输入参数求得如下结果∶
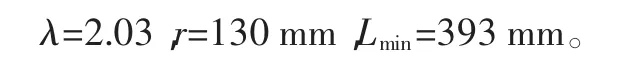
根据r值及大链轮分度圆计算公式d=p/sin(180°/z)可计算出 z=42.68。选取 z=43,由 d=p/sin(180°/z)可得 d=260.98 mm,即r=130.49 mm。
根据 c=λr知,c=263.9 mm;又由 L=c+r知,c=263 mm,折中取c=263.96 mm。故在竖直运动状态时储物料斗回转半径L=394.45 mm,此时L为最小值,完成平动传动结构的优化设计。
3 料斗运动分析及仿真
3.1 料斗运动分析
经设计选用节距为19.05 mm的12A链条,储物料斗总数量为10个,均匀分布在链条上。如图2所示,平动传动结构为非对称结构,但前后两侧与储物料斗的连接点的水平距离与前后两侧链轮水平中心距相同,而且前后两侧的旋转运动完全相同。因此前后两侧的料斗运动情况是相同的。
设大链轮以顺时针作为旋转方向进行旋转,带动链条运动。在运动过程中,为使两个储物料斗之间在整个运行周期中都不发生运动干涉的情况,储物料斗之间应当始终保持着一定间距。由图2中可知,储物料斗的运动存在三个形式:首先是竖直运动,此时两个支撑杆与链条的连接点均未进入圆弧运动段;之后是曲线运动,此时一个连接点进入圆弧运动段,另一个连接点仍处于竖直运动段;最后是圆弧运动,两个连接点均进入圆弧运动段。储物料斗就是按照三种运动形式循环运动。
3.2 运动仿真
利用Pro/E完成整体结构的运动分析实体模型,模型中不包括链传动部分。模型建立好之后导入到RecurDyn中。该软件采用相对坐标系运动方程理论和完全递归算法,非常适合求解大规模以及复杂接触的多体动力学问题[7]。在RecurDyn行业子系统建模工具包Toolkit中具有链传动建模工具箱,完全可以进行参数化设计。模型由电机与同步轴之间的减速链传动、同步轴与两地轴之间的减速齿轮传动和储物料斗两侧的等速链传动构成。其中链传动子模型是通过RecurDyn行业子系统建模工具包中的Chain工具完成。

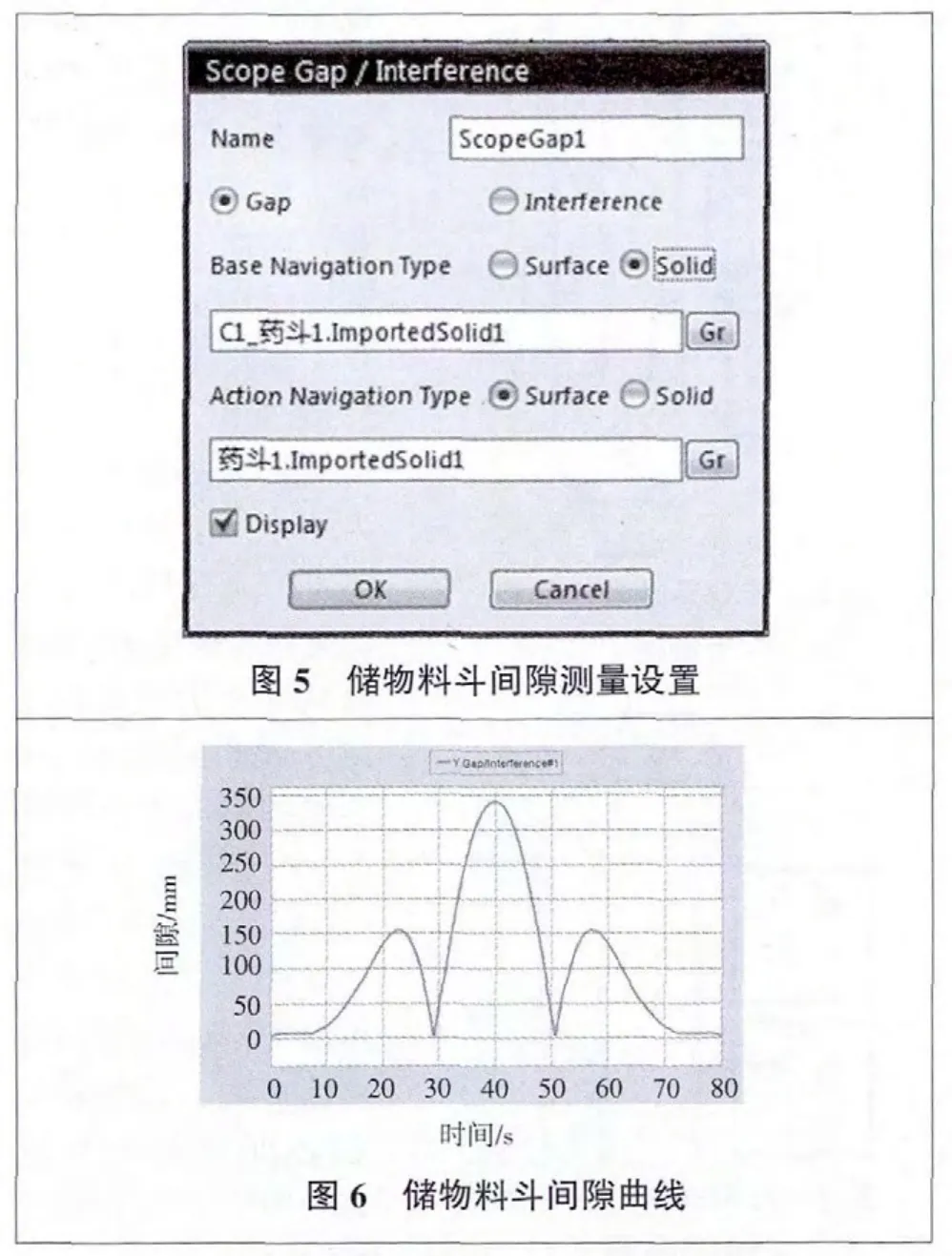
本节重点研究储物料斗的运动不干涉情况,因此只需模型进行机构之间的啮合运动。另外,RecurDyn的分析菜单 Analysis提供了测量仪Scope工具,可以测量两实体或两曲面之间的间隙。图4为储物料斗运动分析仿真图。
在电机轴上的的旋转副施加速度驱动,设置测量仪中的间隙测量参数,将两个储物料斗实体作为测量对象,如图5所示。设置仿真时间为80 s,运行仿真。图6为两储物料斗之间的间隙数据,从图中可以看出,在整个仿真过程中间隙距离一直大于3 mm,可知两储物料斗无运动干涉现象发生。
4 结语
通过分析回转平动传动结构及其工作原理,确定影响结构占用空间的因素,并建立数学模型。利用MATLAB函数计算数学模型,完成了整体结构的优化设计。最后分析储物料都不干涉运动情况,并通过Pro/E和RecurDyn软件对储物料斗进行运动仿真,验证不干涉运动情况和优化设计结果。经过优化设计,使结构紧凑并符合最小占用空间布局。此结构的设计对竖直旋转回转库的设计具有一定指导意义。
[1] 郭鹏.基于CAE的垂直循环立体车库结构设计研究[D].济南:山东大学,2007.
[2] 王吉忠,赵金先.基于托架运动不干涉条件的停车设备链传动系统的设计[J].起重运输机械,2005(10):8-10.
[3] 褚成春.回转柜药房机械结构设计与分析[J].机械设计与制造,2012(7)∶6-8.
[4] 陈婧,田怀文.大型垂直循环横向平移立体车库的结构设计及稳定性分析[J].机械设计,2013(4)∶67-70.
[5] 张志强.立式回转药柜结构优化设计与运动仿真[J].中国机械工程,2010,21(12)∶1423-1429.
[6] 谢中华,李国栋,刘焕进.MATLAB从零到进阶[M].北京:北京航空航天大学出版社,2012∶316-333.
[7] 刘义.RecurDyn多体动力学仿真基础应用与提高[M].北京∶电子工业出版社,2013∶2-26,209-303.

