风力机叶片多体动力学分析

单丽君，叶 炯，李 慧

(大连交通大学 机械工程学院，辽宁 大连 116028)*

0 引言

风能主要是通过风力发电机被人们利用，而风机叶片是风力机的核心部件，决定了发电功率.为了达到更大的发电功率，成为风机叶片的研究热点，最直接的方法就是设计出足够长的风机叶片，随之而来的问题就是叶片柔性增加，风机运行精度的控制要求也越来越高，需要精确的了解风机叶片工作中的动力学响应.大型风力机柔性叶片在其绕风轮轴线转动过程中的弹性变形与旋转运动间的相互影响和耦合，对其气弹稳定性与控制系统设计影响很大，这正是多体系统动力学的核心.近年来，该理论在风力机领域日益受到重视，已被越来越多的研究者引入风力机结构动力学分析中［1］.

本文采用刚柔混合多体系统动力学建模方法将风机叶片离散成一定数量的单元，运用ADAMS/Vibration振动分析模块进行振动仿真分析.以1.5 MW风机叶片为例，计算分析其固有频率和振型，得出了计算风机叶片固有频率及振型的方法，为分析风力机叶片振动研究提供理论依据.

1 Joint beam element建模方法

根据国外学者 Zhao Xueyong，Peter Maiβer，Wu Jingyan 所研究的 Joint beam element［2］模型进行刚柔混合多体系统动力学建模，该单元是由4个刚体组成，形成了一个立体连接的刚体系统.如图1所示.邻近的两个刚体由万向节或圆柱关节连接，B1与B2之间是万向节铰接，B2与B3之间是圆柱关节铰接，体现出惯性力的作用.本模型考虑了风机叶片的挥舞、摆振、扭转和拉伸，有六个自由度，四个旋转度，一个扭转和一个伸长.在工作情况下，叶片受到很大的惯性力的影响，出现比较大的离心力和旋转效应.

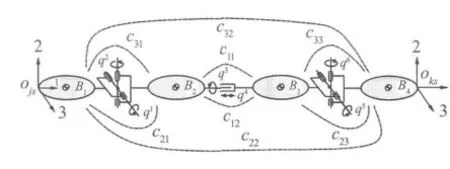
图1 万向关节梁单元模型

2 风机叶片三维建模

2.1 风力机叶片外形设计

1.5 MW风力发电机风轮的直径可以根据以下公式计算:

其中:Cp=0.42为风能利用率;η=η1×η2=0.81为风力发电机传动效率;V=12 m/s为设计风速;ρ=1.225 kg/m3为空气密度.

综合考虑后取D=73 m.1.5 MW风力机叶片长度一般为33～40 m，本文中选取叶片长度为34 m，轮毂直径为2 m.

本文选用NACA4412为标准翼型，由于其良好的气动性能以及较全的翼型数据.采用Wilson设计方法设计叶片的弦长和安装角［3］.在Matlab中设计程序求解叶片各个截面的弦长和安装角.再对叶片的弦长和安装角修正，最后得出相应的弦长和安装角.

通过profili软件获取各截面翼型数据，即二维坐标点(x0，y0).通过坐标转换的方法获得实际坐标.设翼型的气动中心为原点，翼型实际坐标为(x1，y1)，一般气动中心到翼型前缘的距离为0.25 ～ 0.35之间，本文取0.3，所以气动中心坐标为(x3，y3)=(0.3C，0).

经过坐标转换整理得:

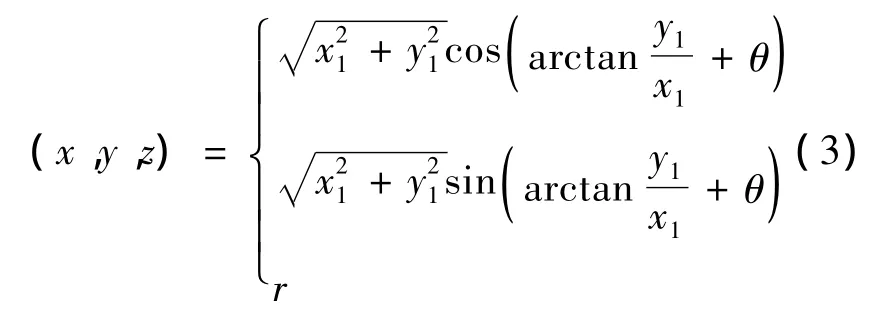
通过Excel可以很快计算出全部截面的实际坐标.将各个截面的实际空间坐标(x，y，z)编辑成文本，文档名后缀为.ibl的文件保存.

2.2 叶片实体建模

叶片的实体建模采用Pro/E强大的自由曲面造型功能来完成［4］.打开 Pro/E，新建模型，插入—模型基准—曲线，然后在菜单管理器中选择来自文件，选择坐标系，打开各个截面的.ibl文件，便可导入翼型曲线.所有翼型缺省视图如图2所示.

图2 所有翼型缺省视图

图3 风机叶片实体模型

得到所有截面后运用边界混合命令，生成叶片曲面，再对其进行光滑修型处理.利用填充命令将根部和叶尖的截面进行填充处理，合并三个曲面，最后进行实体化处理，得到叶片实体模型.风力机叶片三维实体模型如图3所示.

3 风机叶片动力学仿真

3.1 振动仿真

将风机叶片三维模型在Pro/E中完成分段，按照Joint beam element方法离散化，将叶片按一定的距离分成10段.将Pro/E模型导入到MSC.ADAMS中，对每个Part进行修改，设置其材料特性、重量、颜色等，再给模型添加弹簧、阻尼器、万向关节，圆柱副等约束.如图4所示.

图4 叶片Joint beam element模型

1.5 MW风力机额定转速下，风轮是以19 r/min转动的，对模型设置相应的激励后，在ADAMS/Vibration模块中建立振动仿真分析［5］.经过仿真计算得到叶片静止和工作状态下固有频率如表1所示.

表1 振动分析结果

利用GH-Bladed软件对该风力机叶片建模、设置相应参数后，进行仿真计算，得到了1.5 MW风力机叶片的固有频率结果.如图5及表2所示.

图5 风力机叶片模型

表2 Bladed计算结果

对仿真结果进行误差分析可得，两个软件所求的固有频率存在一定的误差，经过分析可知，在ADAMS中所设置的载荷比较单一，没有Bladed中设置的完善，所以计算产生的误差比较大.在对静止和工况下的固有频率进行比较分析可知，两种软件计算下的旋转工作下的固有频率都有所增加.出现这种现象的原因是在旋转工况下风力机叶片的离心惯性力和风压力的耦合作用下，风力机叶片出现刚化［6］，刚度有所增加，导致振动幅值减小，固有频率就有一定的增加.

由频域曲线图6可知，当频率在0.774 2、3.398、10.46、26.96 和30.34 Hz 时的振幅比较大，这些峰值点接近第一、二、四和第八阶的固有频率，一般只研究低阶的固有频率，所以只考虑前五阶固有频率，频域曲线中的峰值频率点是叶片振动幅值比较大的地方，如果叶片的固有频率和这些点靠近会发生共振现象，对叶片造成破坏作用，在设计制造叶片时需要避开这此频率点，防止共振对风力机叶片的损坏.

图6 频域曲线

叶片的振型由图7可知，叶片第一阶振型为挥舞.叶片第二阶振型为摆振.叶片第三阶振型为挥舞.叶片第四阶振型为摆振为主.从前四阶模态分析中得出风力机叶片中间和弦长最大的位置弯曲变形比较厉害，时间一长容易出现疲劳破坏现象，在设计制造时要加强此位置范围的强度.前四阶的风力发电机叶片的振动形式主要是挥舞和摆振，综上所述，风机叶片主要的振型为挥舞和摆振.

图7 叶片模态图

4 结论

(1)以1.5 MW风力机叶片为例，应用Joint beam element的建模方法，建立了风力机叶片的刚柔混合动力学分析模型，运用MSC.ADAMS求解器中的ADAMS/Vibration振动模块计算了额定转速工况下风力机叶片的固有频率和振型;

(2)模态分析结果表明叶片发生破坏的具体区域是叶片中间到弦长最大的位置，通过频域分析，获得了振动幅值较大的频段范围，为找出振动影响因素，提供参考;

(3)采用GH-Bladed软件进行了分析和验证，分析结果表明所建的刚柔混合模型是基本正确的.

［1］洪嘉振，蒋丽忠.柔性多体系统刚柔耦合动力学［J］.力学进展，2000，30(1):15-20.

［2］ZHAO XUE YONG，PETER MAIβER，WU JING YAN.A new multibody modelling methodology for wind turbine structures using a cardanic joint beam element［J］.Renewable Energy，2007，32(3):532-546.

［3］邬再新，崔琦，刘涛，等.兆瓦级风力发电机叶片外形设计及三维建模［J］.机械与电子，2013(7):75-77.

［4］陈圆.风力发电机叶片三维建模及有限元动力分析［D］.西安:西安理工大学，2008.

［5］李增刚.ADAMS入门详解与实例［M］.北京:国防工业出版社，2006:211-222.

［6］李德源.风力机旋转风轮振动模态分析［J］.太阳能学报，2004，25(1):72-77.