接触式轮轨外形测量仪器的半径补偿方法

向文明，江海琳，沈 钢

(同济大学 铁道与城市轨道交通研究院，上海 201804)*

0 引言

由于车轮和钢轨的断面外形在铁道车辆横向动力学行为中起支配作用，准确获取车轮与钢轨的断面外形成为一件重要工作.对于轮轨外形的测量，按测量原理可以分为接触式和非接触式两类［1］.目前，接触式以其测量精度高、稳定和测量范围大而被大量采用.国内外的接触式测量仪器其测量连杆末端都连接有测量轮，测量滚轮滚过测量对象表面即能测出断面轮廓的外形.杆机构带动编码器旋转，测量系统采集到角度数据.通过角度数据和数学计算模型只能得到测量轮的轮心坐标，要想得到被测对象的实际轮廓曲线的坐标数据，还需要对轮心轨迹数据进行滚轮半径长度的偏移，通常我们称这一过程为半径补偿.

当前，对于上述的半径补偿问题方法众多，包括测量方向补偿法、线线补偿法、二点补偿法、三点共圆补偿法、B样条曲线逼近法等［2］.相关的研究所采用的方法大多都是有其适用条件的，对任意形状的轮心曲线进行半径补偿效果并不稳定.本文根据补偿时求导方式的不同，分别用了三点平均导数法和高阶傅里叶函数拟合法这两种方法实现补偿，并通过巧妙的算法设计使其能对任意曲线进行半径补偿.在离散点足够密集的情况下，三点平均导数法和高阶傅里叶函数拟合法都是有效的方式，离散点稀疏的情况下高阶傅里叶函数拟合法更优.

1 半径补偿原理

在滚轮滚过测量表面时，滚轮始终是与测量表面相切的(图1).滚轮轮心在任意的(xo，yo)位置时，始终有对应的唯一切点(x，y)，且点(x，y)位于滚轮轮心坐标(xo，yo)的法线方向.

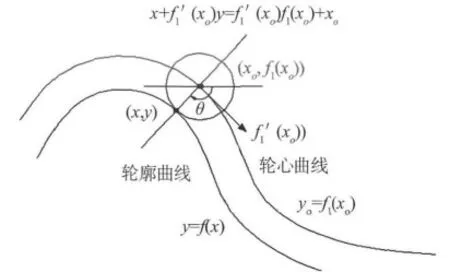
图1 半径补偿原理图

假设滚轮轮心曲线方程为yo=f1(xo)，轮廓曲线的方程为y=f(x)，滚轮半径为R，点(xo，yo)法线与水平轴间的夹角为θ.对于轮心曲线上的任意一点(xo，yo)，切点(x，y)可以通过如下方程求解组求解:

方程组(1)有两个解，而轮心曲线内侧解是我们所求的.

由方程组(1)可求得:

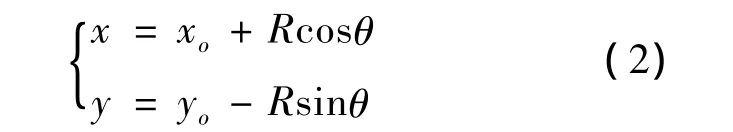
其中:

cosθ和sinθ的正负号取值根据轮心曲线的走向而定.

求得轮心曲线上每个(xo，yo)点对应的导数值f1'(xo)，即可根据式(2)得到对应的轮廓曲线上的点(x，y).

2 半径补偿的实现

由半径补偿的原理可知，实现半径补偿的关键在于求得轮心曲线上每个离散点的准确导数值.因此，根据离散点求导方式的不同使用了两种方式实现.

2.1 三点求导法

测量仪器得到的轮心曲线是由离散点构成的，通常这些离散点是十分密集的(间距在0.5 mm左右).因此轮心曲线上某点(xi，yi)的导数值可以用下式近似:

其中坐标点(xi-1，yi-1)和(xi+1，yi+1)表示点(xi，yi)的相邻两点.

2.2 高阶函数拟合求导法

用高阶傅里叶表达式拟合轮心曲线，从而求得轮心曲线的解析式，再对解析式求导，即可求得轮心曲线任意坐标位置的导数值［6］.

n阶傅里叶拟合表达式为:

假设轮心曲线由 (x1，y1)，(x2，y2)，… (xi，yi)，…(xm，ym)m个离散点构成，由拟合方程(4)可知:

令则式(5)可以写成XM=Y.

基于最小二乘条件下的拟合系数矩阵解M应满足J=‖XM-Y‖min=((XM-Y)T(XMY))min.由，可得矩阵

M=(XTX)-1XTY

2.3 算法设计

使用上述两种方法对轮心轨迹曲线直接求导后代入式(2)，补偿任意的轮轨廓型时效果并不理想(图2).这是由于在轮心轨迹曲线的竖直线部分，轮心坐标的导数值在正负无穷大来回跳动，导致补偿的方向无法准确判断，补偿的结果数据点也相应地跳变.

为了克服上述的补偿结果跳动的问题，基于曲线在坐标系中的旋转变换并不改变曲线的形状的思想，设计了巧妙的轮轨廓型半径补偿算法.补偿算法能适应任意形状的轮心曲线.

图2 轮轨廓型的补偿效果

基于三点求导方式下的补偿算法:

(1)对于轮心曲线上的除首位两点外的任意点 (xi，yi)，计 算 其 与 相 邻 两 点 (xi-1，yi-1)、(xi+1，yi+1)的横、纵坐标差的绝对值最小值mindx=min(|xi-xi-1|，|xi+1-xi|，|xi+1-xi-1|，mindy=min(|yi-yi-1|，|yi+1-yi|，|yi+1-yi-1|);

(2)如果mindx＞mindy，则转(3)，否则转(4);

(3)xi点处的导数值为f'(xi)=.如果xi+1＞xi-1，则 cosθ否则 cosθ.补偿后的轮廓外形坐标点为(xi+Rcosθ，yi-Rsinθ);

(4)令 xnew1=yi-1，ynew1=-xi-1，xnew2=yi，ynew2=-xi，xnew3=yi+1，ynew3=-xi+1.变换后，对应点的导数值为如果 xnew3＞ xnew1，则 cosθ=，否则.补偿后的轮廓外形坐标点为(-ynew2+Rsinθ，xnew2+Rcosθ).

基于高阶函数拟合法求导法设计的半径补偿算法与基于三点求导法设计的算法思路相似.拟合法先将轮心曲线分段拟合，拟合前先根据分段曲线的特征来判断是否需要相对坐标作旋转变换，及旋转多少角度的变换.将旋转变换后的某段轮心曲线用高阶傅里叶函数拟合后，求出变换后的轮心曲线的半径补偿点，再将这些补偿点作逆向等角度的旋转变换后得到的点即为实际的轮廓外形数据点.

改进后的半径补偿算法能适应任意形状的轮心曲线(图3).

图3 改进补偿算法的补偿效果

3 算法测试

将上述的两种半径补偿算法编写为C++代码嵌入到与轮轨外形测量仪器配套的数据处理与分析软件中.通过使用实际的轮轨外形测量仪器(图4)测量并将测量结果与标准验证样块进行比较，结果表明:在设置测量仪器角度编码器采样步长控制脉冲数为40(影响数据采集疏密程度的参数)时，基于三点求导法和高阶傅里叶函数拟合求导法的半径补偿算法均能实现较理想的半径补偿效果，补偿的最大偏差能控制在1 μm以内，这远小于角度编码器自身精度带来的的误差值.步长控制脉冲数进一步减小时，算法的补偿精度提高不明显.步长控制脉冲数增加到一定程度，轮心曲线数据更稀疏后，可以发现采用基于拟合求导方式的半径补偿算法更优.算法的补偿偏差只来源于轮心坐标的导数值误差，理想上当轮心坐标的导数值完全准确时，补偿的结果没有偏差.对于轮心曲线变化急剧的位置，离散点过于稀疏后，采用三点求导法(按式(3)计算)求得的导数值就不再精确了，因而补偿的偏差就会较大.为保证半径补偿的精度，建议在设置仪器编码器采样步长的脉冲控制数不高于40.

图4 轮轨外形测量仪器及测试验证模块

4 结论

本文研究了用于接触式轮轨外形测量数据处理的半径补偿算法.通过算法设计，使得半径补偿算法能够适应任意形状的轮心曲线.经实际仪器测量，验证了设计的补偿算法的有效性及高精度，同时也指出了半径补偿方法的补偿偏差来源，指出了保证补偿精度的条件.

［1］沈钢，黎冠中，李小江，等.轮轨踏面外形的实际测量及几何接触的进一步研究［J］.铁道学报，1999(5):24-28.

［2］朱冰冰.便携式钢轨测量仪的改进及检验［D］.成都:西南交通大学，2014.

［3］卢红，张仲甫.测头半径补偿的方法［J］.组合机床与自动化加工技术，2001(10):41-43.

［4］王凌云，和延立，姚伟.数控系统的刀具半径补偿技术研究［J］.浙江工业大学学报，2005(2):219-222.

［5］颉赤鹰，陈少克.三坐标测量机测头半径补偿的新方法［J］.组合机床与自动化加工技术，2006(1):50-52.

［6］蔡山，张浩，陈洪辉，等.基于最小二乘法的分段三次曲线拟合方法研究［J］.科学技术与工程，2007(3):352-355.

［7］代冬岩，李智勇，张宏礼.最小二乘曲线拟合及其MATLAB 实现［J］.黑龙江科技信息，2009，21:36.

［8］陈纪修.数学分析 (第二册)［M］.2版，北京:高等教育出版社，2004:405-425.