改进的遗传算法求解柔性作业车间调度问题

刘月凡，朱 星

(大连交通大学软件学院，辽宁 大连116028)*

0 引言

作业车间调度问题(Job-shop scheduling problem，JSP)是研究生产线调度问题最常用的模型之一［1］，也是实现先进制造和提高生产效率的基础和关键［2］.柔性作业车间调度问题(Flexible jobshop scheduling problem，FJSP)是传统作业车间调度问题的扩展，在传统的作业车间调度问题中，每个工件的加工工序是确定的，每一道工序的加工机器和加工时间也是确定的，而在柔性作业车间调度问题中，每个工件的每一道工序可以在多个可选择的加工机器上进行加工，并且不同的加工机器所需要的加工时间是不同的，增加了调度的灵活性，比较符合生产的实际情况［3］.

柔性作业车间调度问题已经被证明是更复杂的NP-Hard问题，因而难以取得最优解.目前，求解FJSP的常用方法有禁忌搜索(TS)，模拟退火(SA)和遗传算法(GA)等［4-6］.其中遗传算法以其操作简单、鲁棒性强、搜索全局最优解速度快等特点，在生产调度领域得到了广泛的应用.

遗传算法是由美国J.Holland教授于1975年提出的，是一种模拟自然进化过程的一种优化算法.由于传统的遗传算法存在着较大的缺陷，国内外学者已从不同角度对其进行了改进，本文对传统遗传算法的初始种群进行了改进，以提高初始解的质量.

1 柔性作业车间调度模型

设有 n个待加工工件 J(J1，J2，…，Jn)，在 m台设备上加工 M(M1，M2，…，Mm)，每个工件 Ji有Pi(Pi1，Pi2，…，Pin)道工序，每道工序可在一台或多台设备上加工，同一道工序在不同设备上加工的时间可能不等，工序 Pik的可选机器集为Mik(Mik⊆M)，每台设备的加工时间从0开始，加工完所有工件的完成时间为ETMi.本文以最小化最大完工时间为性能指标，其目标函数为:

f(x)=min(max(ETMi))，1≤ i≤ m

模型需满足如下约束条件:

(1)同一工件的工序加工顺序确定;

(2)每道工序必须在它的上一道工序加工完成后才能开始加工;

(3)每道工序只能选择一台设备进行操作;

(4)每台设备在同一时间只能加工一个工件的一道工序;

(5)每道工序在设备上操作时都不允许被中断;

(6)不同工件工序之间没有先后约束条件.一个包含3个工件、5台机器的FJSP的问题描述如表1所示.

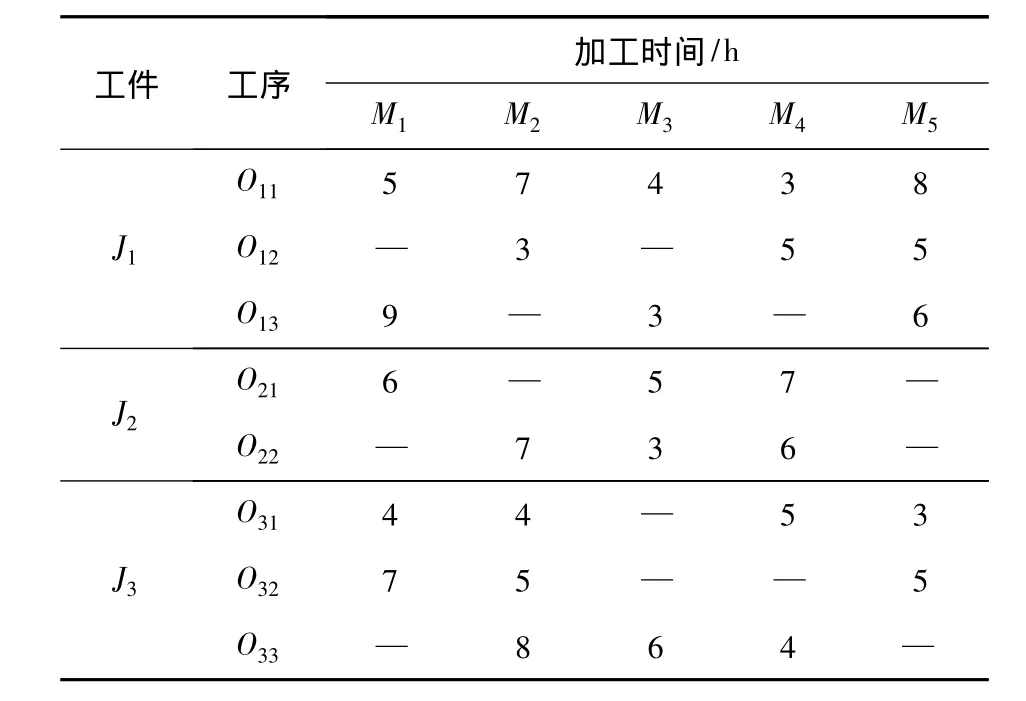
表1 3×5 FJSP问题加工时间表

2 算法的设计

(1)基因编码

常用的遗传算法编码方案有二进制编码、格雷码编码、矩阵编码、自然数编码等，本文采用自然数编码，每条染色体表示一个可行解，同时采用双层编码，第一层编码为基于工件的工序编码，编码长度为所有工件工序之和，基因值代表工件号，基因值出现的次数代表该工件的工序总数，第二层编码为对应于第一层工件工序的机器编码，所以编码长度也为所有工件工序之和.以表1为例，图1中染色体表示的工序顺序为 (O31，O11，O12，O21，O22，O32，O13，O33)，染色体表示的机器序列为(M2，M4，M2，M1，M4，M5，M3，M4).

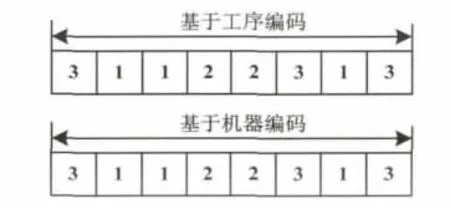
图1 基于工序和机器的编码

(2)产生初始种群

初始种群的优良对生物进化会产生很大的影响，本文对初始种群的机器选择进行了改进，首先随机生成初始种群的工序编码，工序编码生成后就要对应生成机器编码，每个工件工序在对应可选机器集中选择机器时，是以不同的概率的来选择不同的机器，机器加工时间短的以大概率被选择，相比之下，机器加工时间长的以小概率被选择，这样既保证了机器选择的随机性，也优化了初始种群.

(3)适应度函数的确定

本文以最小化最大完工时间为目标函数，故选择全部工件完工时间作为评价种群优劣的标准，设n个待加工工件在m(M1，M2，…，Mm)台设备上加工，所有加工工件工序在设备上的最后完工时间为 ETMi(i=1，2，…，m)，T=max(ETMi)，则适应度函数fi=1/T，T越小，则适应度越大，即个体越优.

(4)选择

选择操作的目的是为了保留优良个体，使他们可以遗传到下一代.本文采用精英保留策略和轮盘赌法相结合的方法，对父代个体和子代个体进行选择时直接将最优个体和次优个体遗传到下一代，然后对剩余的个体采用轮盘赌法进行选择，选择出p-2个个体到下一代进行遗传操作.若种群规模为p，个体i的适应度为fi，则个体i被选择的概率pi为

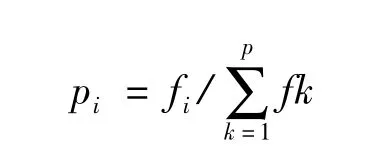
即适应度越高的个体被选择的概率就越大.

(5)交叉

交叉操作是产生新个体的主要方法，提高全局搜索能力［7］.本文采用单点交叉方式，即随机产生一个交叉点，交换交叉点后的基因.从种群中随机选择两个个体，交换两个个体工序编码的交叉点后面的基因，将交叉后工件多余的工序替换为其他工件缺失的工序;机器部分则按交叉前工件工序所选择的机器进行相应调整以保证其子代染色体的合法性.

(6)变异

变异操作的目的是改变算法的局部搜索能力，有助于维持进化群体的多样性，防止过早陷入局部最优［8］.本文采用互换方式，即随机产生两个变异点，交换两点的基因值.从种群中随机选择一个个体，对该个体的工序编码部分随机产生两个变异点，交换两点的基因值，同时将交换的基因位所对应的机器号也进行交换.

3 仿真实例分析

表2给出了6×6(6个工件，6台机器)FJSP的加工工序，机器选择和加工时间矩阵表.分别用标准遗传算法和本文提出的改进遗传算法对工件最小化最大完工时间进行优化计算，并分析优化计算结果.

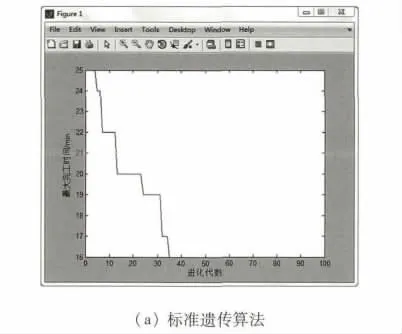
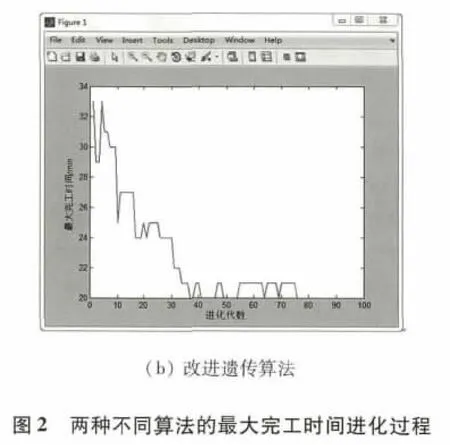
遗传算法采用以下参数:种群规模为100，进化代数为100，交叉概率Pc=0.8，变异概率Pm=0.1.算法运行10次，最优的选择如图2、3所示.

表2 6个工件在6台机器上FJSP实例

从图2，3中可以看出，标准遗传算法的最大完工时间为20，收敛代数为75代左右;改进遗传算法的最大完工时间为16，收敛代数为35代左右.改进遗传算法既缩短了工件完工时间，也加快了收敛代数.从而验证了改进遗传算法的可行性.

4 结论

传统遗传算法在进行种群初始化时采用的大多是随机选择方式，而本文提出了一种新的种群初始化方法，提高了种群初始解的质量.最后对改进遗传算法进行了仿真实验，并将结果与标准遗传算法进行比较，结果表明了本算法的优越性和可行性.

［1］JAIN A S，MEERAN S.Deterministic job-shop scheduling:Past，present and future［J］.European Journal of Operational Research，1999，113(2):390-434.

［2］彭建刚，刘明周，张铭鑫，等.基于改进非支配排序的云模型进化多目标柔性作业车间调度［J］.机械工程学报，2014，50(12):198-205.

［3］张国辉，石杨.基于改进遗传算法求解柔性作业车间调度问题［J］.机械科学与技术，2011，30(11):1890-1894.

［4］MASTROLILLI M，GAMBARDELLA L M.Effective neighborhood functions for the flexible job shop problem［J］.Journal of Scheduling，2000，3(1):3-20.

［5］张维存，郑丕谔，吴晓丹.蚁群遗传算法求解能力约束的柔性作业车间调度问题［J］.计算机集成制造系统，2007，13(2):333-362.

［6］张超勇，饶运清，李培根，等.柔性作业车间调度问题的两级遗传算法［J］.机械工程学报，2007，43(4):119-124.

［7］李运霞，杜娟，孙王路.基于多种群遗传算法的路径柔性车间调度问题［J］.组合机床与自动化加工技术，2014(3):152-155.

［8］周俊虎，平传娟，刘建忠，等.基于遗传算法的动力配煤模型［J］.煤炭学报，2003，28(5):547-551.