基于高频面板数据的人民币汇率波动规律研究

余 菊

(重庆理工大学 经济与贸易学院，重庆 400054)

基于高频面板数据的人民币汇率波动规律研究

余 菊

(重庆理工大学 经济与贸易学院，重庆 400054)

基于2006—2013年的1 771个人民币汇率日值高频数据，采用GARCH模型对人民币与美元、港币、日元、欧元及英镑之间的汇率波动规律进行实证分析。结果显示：(1) 人民币兑五大外汇币种汇率的波动存在ARCH效应，其收益表现出明显的群聚特征；(2) 人民币兑五大外汇币种汇率的波动均具有一定的记忆性，但除港币和日元外，大都会随时间缓慢衰减；(3)人民币兑五大外汇币种汇率的波动存在明显的杠杆效应，但不同币种对人民币升值的反应存在一定的差异。

人民币汇率；波动效应；GARCH模型；高频数据

自2005年汇改以来，人民币兑几大关键外币的汇率基本呈升值态势，虽受2008年金融危机的影响人民币暂停了升值走势，但到2010年以后，由于重启冻结的汇率制度，特别是在2012年4月央行加大了汇率波动幅度，汇率波幅由0.5%扩大到1%，人民币汇率又继续呈升值趋势，汇率市场化程度明显增强，波动更具弹性。种种迹象表明，增强人民币汇率弹性、促进人民币国际化是大势所趋。然而，汇率的频繁波动可能对我国的国际贸易、投资及资本流动造成冲击。因此，研究汇率的波动效应和波动规律具有重要的理论及现实意义。

一、文献回顾

有关金融资产价格的波动率，国外学者进行了大量的实证研究，在研究方法和技术层面上不断创新，得出了比较有意义的成果。其主要代表有：Engle引入了条件方差的概念，构建了自回归条件方差(ARCH)模型[1]；Bollerslev将滞后条件方差也考虑进来，提出广义自回归条件异方差(GARCH)模型[2]；假定金融资产的预期收益与风险成比例，将风险引入到均值方程后，Engle等构建了ARCH-M模型[3]，随后Chou又提出了GARCH-M模型[4]；为了考察外部冲击对金融市场波动的非对称性，Nelson构建了EGARCH模型[5]，随后Zakoian又提出了TGARCH模型[6]。

国内学者有关波动率的研究大都集中于股市和期货市场方面，而有关描述我国汇市波动的文献相对较少。近年来，随着人民币汇率波动的不断加剧，学者们开始重视对其波动率的研究。骆珣采集了2003—2007年的1 069个美元兑人民币汇率日值,应用GARCH模型进行分析，证实了我国外汇市场确实存在ARCH效应[7]。翟爱梅GARCH族模型的实证研究表明，人民币的汇率收益具有显著的左厚尾特征，其波动具有集聚性和记忆性，随时间变化不会衰减，同时还认为人民币的汇率波动存在一定的杠杆效应，人民币汇率还不具备浮动汇率的特征[8]。常振海把小波多分辨分析理论和去噪理论引入人民币兑港元汇率时间序列，采用AR(1)-GARCH(1,1)拟合模型，同时检验了其波动序列不具有明显的杠杆效应[9]。夏强采用双门限非线性的GARCH模型，选取了人民币兑美元、欧元、日元、港元汇率数据进行分析，发现了门限非线性的结果，认为非美元汇率收益的均值和波动同时表现出非对称的特点[10]。孙映宏基于2010年1月1日至2012年5月10日的中美汇率日值，利用GARCH模型进行实证检验，认为其残差存在异方差性[11]。谢非等基于GARCH模型对企业汇率风险进行了测量[12]。

已有的文献对人民币汇率的波动效应及波动规律进行了一些有意义的经验研究，但就总体而言，在研究对象上大多只针对人民币与某一种关键货币的汇率波动作实证研究，忽略了我国不同币种结构对汇率波动反应的差异性。然而不同外币结构对人民币汇率波动的反应有可能存在一定差异，有必要分币种考察。因此，本文在对人民币汇率波动的描述性统计基础上，采取GARCH和Threshold GARCH模型对人民币与主要外汇币种汇率的波动规律及波动效应进行实证分析。

二、人民币汇率日收益率数据统计特征分析

本文选取了2006年8月1日至2013年11月15日区间人民币兑美元、港币、日元、欧元和英镑的每个外汇交易日中间牌价的1 772个日高频数据观测值，其时间序列如图1所示。

图1 2006—2013年人民币兑五大外汇币种的日汇率走势

从人民币兑美元汇率的走势来看，大致经历了三个阶段：从2005年汇改到2008年金融危机爆发前，人民币兑美元汇率从“8”字头急剧升值到“7”字头；而2008年金融危机的爆发使得人民币兑美元汇率的升值步伐放缓，汇率稳定在“6.8”水平并持续了两年；但从2010年9月起，人民币兑美元汇率又处于快步升值阶段，从“6.8”升值到2013年的“6.1”水平。

由于港币对美元实行的联系汇率制，故人民币兑港币汇率也经历了与美元汇率走势大致相同的三个阶段：从2005年汇改到2008年金融危机爆发前，人民币兑港币汇率从“1.04”急剧升值到“0.83”水平；而2008年金融危机的爆发使得人民币兑港币汇率的升值步伐放缓，汇率稳定在“0.83”水平并持续了两年，但从2010年9月起，人民币兑港币汇率又处于快步升值阶段，从“0.83”升值到2013年的“0.79”水平。

与此同时，人民币兑日元汇率的走势却总体呈现出倒U型波动轨迹：2011年以前，人民币兑日元汇率基本呈贬值趋势，从100日元兑6.9元人民币，贬到2012年初的100日元兑8.2元人民币；但从2012年2月始，人民币兑日元汇率开始大幅度升值，到2013年11月100日元兑6.1元人民币。

另外，由于欧洲经济共同体原因，人民币兑欧洲国家货币的走势大致趋同。其中，人民币兑欧元的汇率经历了波浪式的升值过程，而人民币兑英镑的汇率也经历了2008年前的急剧升值以及2008年后的波浪式缓慢升值过程。

总体而言，人民币兑美元及港币的汇率走势大致趋同，均经历了2008年前的急剧升值、两年多的平稳期、2011年后再度升值三阶段；同时，人民币兑欧元及英镑走势也同样趋于一致，均经历了较为明显的波浪式升值过程；而人民币兑日元汇率的走势却总体呈现出倒U型波动轨迹。

三、研究设计

(一)GARCH族模型的构建

为了更好地描述汇率波动的持续性，传统ARCH模型由于加入过多的滞后阶数，因而在应用上存在局限性。而大量文献证实，考虑在条件方差方程里加入条件方差的滞后项的GARCH模型能很好地描述金融市场波动的持续性，因此，在实证检验中建立GARCH模型。这里采用GARCH(1,1)模型：

均值方程：

yt=πxt+ut

方差方程：

(1)

在金融应用中，一般假定资产的预期收益与其风险是成比例的，因此，我们可以在均值方程中再引入误差序列的条件方差或条件标准差，得到GARCH(1,1)-M模型：

均值方程：

方差方程：

(2)

为了考察人民币汇率的波动是否存在杠杆效应，本文还建立TGARCH或TGARCH-M模型：

方差方程：

(3)

其中，dt为虚拟变量，当ut>0时，dt为0，否则为1。由此可见，汇率升值冲击时(ut<0)和贬值时(ut>0)对条件方差的作用效果不同。利好信息的影响系数为α，利坏信息的影响系数为α+γ，若γ≠0，则说明条件方差对冲击的反应是非对称的，也即存在杠杆效应。

(二)样本区间和数据来源

目前国内金融机构及各大企业所持有的外币资产主要为美元(USD)、港币(HKD)、日元(JPY)、欧元(EUR)和英镑(GBP)，故本文选取人民币兑这些主要外汇币种的汇率收益作为风险因子，同时，这里的人民币兑五大外汇币种的汇率均采用直接标价法。

由于2006年8月1日前的人民币兑英镑汇率数据有缺省，因此本文的样本区间选取为2006年8月1日至2013年11月15日区间人民币兑美元、港币、日元、欧元和英镑的每个外汇交易日中间牌价的1 772个日高频数据观测值。原始数据来自中国人民银行网站，缺省数据来自国家外汇管理局。

将人民币汇率序列作对数处理，使其变成比较平稳的收益性序列(见图2)，这样人民币兑主要外汇币种的汇率收益为：

四、实证结果与分析

(一)GARCH模型滞后阶数的确定

本文采用根据人民币兑美元、港币、日元、欧元和英镑汇率波动的AC值绘制的自相关函数图来确定GARCH模型的滞后的阶数(取AC值绝对值大的阶数)。

通过图3汇率收益Rt的自相关函数可以看出，日收益率相关性比较显著的有：美元滞后20和35阶；港币滞后1、3、19和35阶；日元滞后2和10阶；欧元滞后25阶；英镑滞后13和23阶。相应地，人民币兑各大主要外汇币种的汇率收益rt的均值方程采用相应的滞后阶数。

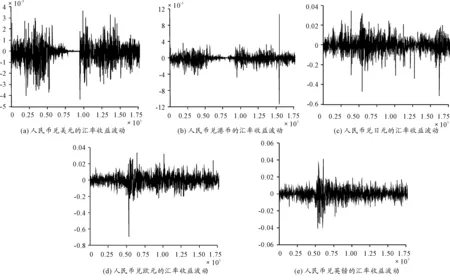
图2 2006—2013年人民币兑五大外汇币种的汇率收益波动图

图3 2006—2013年人民币汇率收益的自相关函数

(二)GARCH模型的估计

为了验证人民币兑五大外汇币种的汇率波动是否具有ARCH效应以及是否随时间推移而缓慢衰减，先利用前面的GARCH模型(见式1)或GARCH-M模型(见式2)进行估计，结果见表1。

由表1的均值方程估计结果可知，参数估计系数是显著的，说明GARCH(1，1)模型能够较好地拟合数据，汇率的波动具有集聚性。

方差方程中的α反映冲击对波动的影响，β反映了系统的长期记忆性，α+β反映波动的持续性。从GARCH(1，1)的估计结果来看，人民币兑五大外汇币种汇率收益的ARCH项系数α均大于零，这说明反映外部冲击会加剧汇率的波动。同时，人民币兑五大外汇币种汇率收益的GARCH项系数β均小于1，且十分接近1，这说明汇率波动具有一定的记忆性，即汇率波动具有一定的持续性。另外，除港币外，人民币兑美元、日元、欧元及英镑汇率收益的GARCH模型α+β均小于1，且十分接近1，满足参数的约束条件，说明外汇市场上某时刻的收益冲击将有持续的影响，但波动性随时间变化会缓慢衰减。可能的解释是，人民币汇率自2005年汇改以来，对主要外汇币种的汇率波动逐渐加剧，而且大幅度的波动一直持续2年之久，但自2008年金融危机之后汇率波动幅度收窄，直至当前人民币升值压力依然较大，汇率波动又与危机发生前水平也基本持平。

(三)汇率波动的非对称性检验

为了验证人民币汇率的波动是否存在杠杆效应，据以往经验采用TGARCH(1，1)来刻画。其中，人民币兑美元及港币的汇率采用TGARCH-M模型来估计，而人民币兑日元、欧元及英镑的汇率采用TGARCH模型(由于人民币兑日元、欧元及英镑的汇率TGARCH-M模型估计时，M项并不显著，故应去掉M项)来估计，具体的估计结果见表2。

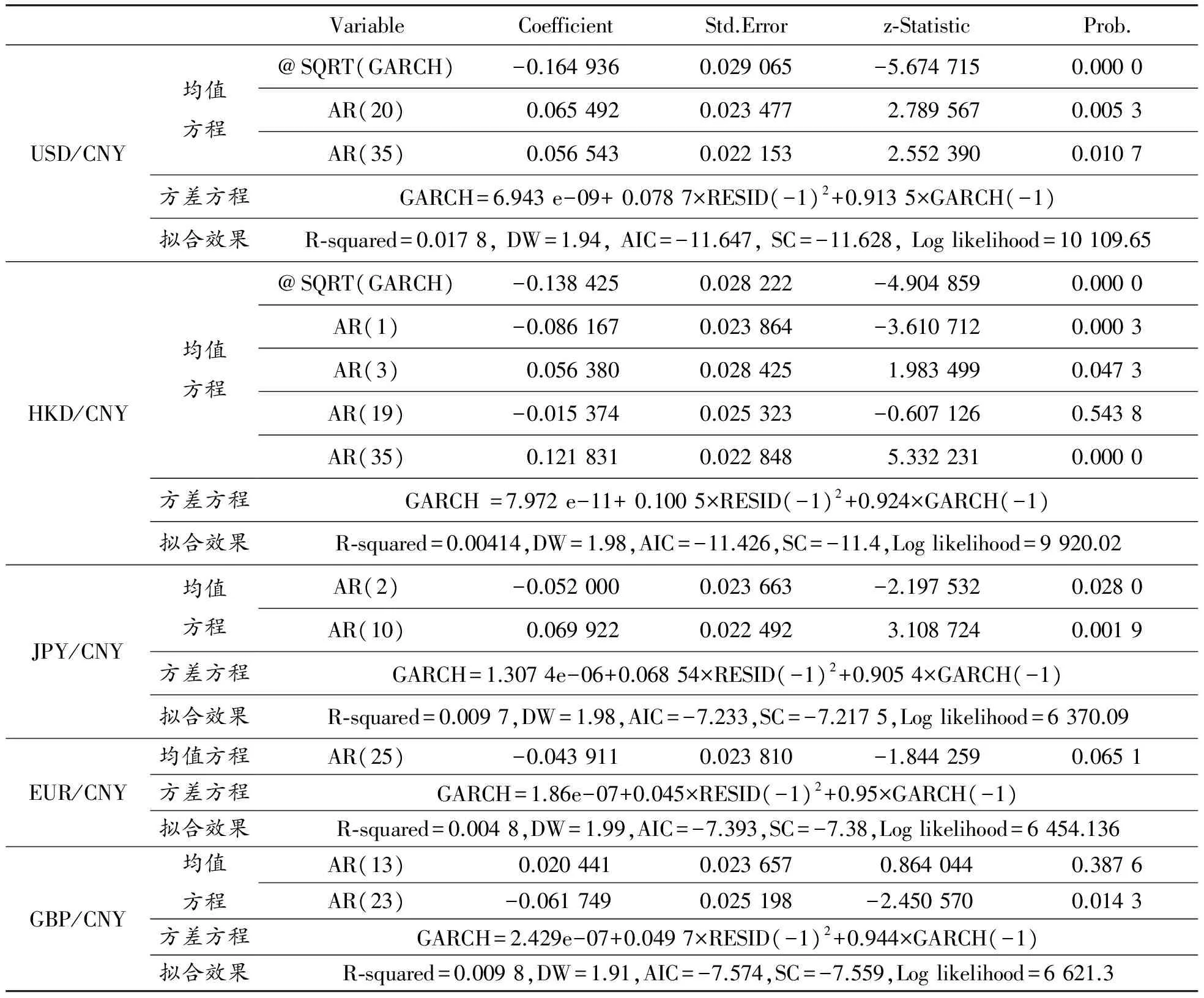
表1 GARCH模型估计结果

表2 TGARCH模型估计结果

根据表2的估计结果，人民币兑五大外汇币种汇率收益的ARCH项系数α均大于零，这进一步证实外部冲击会加剧汇率波动的结论。同样，人民币兑主要外汇币种汇率收益的GARCH项系数β均小于1，且十分接近1(港币汇率除外)，这进一步印证了汇率波动具有一定的记忆性的观点。另外，除港币和日元外，人民币兑美元、欧元及英镑汇率收益的TGARCH模型中α与β之和均小于1，且十分接近1，说明波动性会随时间的推移缓慢衰减。

从TGARCH的估计结果来看，人民币兑五大外汇币种汇率收益的γ项均不为0，并且在1%显著性水平下高度显著，这说明人民币汇率的波动存在明显的杠杆效应。其中，人民币兑美元、欧元及英镑的γ项为正，说明人民币兑这3种货币的汇率升值带来的冲击大于贬值带来的冲击。可能的解释是：当人民币汇率升值时，市场往往会出现持续的升值预期，因而人民币汇率的升值往往会导致更大的波动幅度；而当人民币汇率贬值时，由于国际社会的施压以及贸易顺差压力，使得汇率的贬值幅度小于升值幅度。但实证结果中，人民币兑港币及日元的γ项为负，则说明人民币兑港币及日元的汇率升值带来的冲击小于贬值带来的冲击，这与欧美国家货币的反应正好相反。可能的解释是：香港和日本均属亚洲经济体，与中国的贸易依存度也相对较高，因而其货币对人民币走势的反应也区别于欧美国家，呈现出明显的区域化差异。

五、结论与政策启示

基于2006—2013年的1 771个人民币汇率日值高频数据，采用GARCH模型对人民币与美元、港币、日元、欧元及英镑之间的汇率波动规律进行实证分析。结果显示：(1) 人民币兑五大外汇币种的汇率波动存在ARCH效应，其收益表现出明显的聚群特征，异方差现象普遍存在；(2) 对GARCH及GARCH-M模型的估计表明，α1+β1的和很接近1，说明收益冲击具有一定的记忆性，会持续较长的时间，但多会随时间缓慢衰减(港币和日元除外)；(3)通过TGARCH模型的实证结果显示，人民币兑主要外汇币种的汇率波动存在一定的杠杆效应，人民币升值对收益的冲击大于其贬值的冲击效果(港币和日元除外)。

基于结论，得到如下政策启示：

一方面，适度加大汇率浮动幅度，增强人民币汇率弹性。自2005年汇改以来人民币基本呈升值态势，但受2008年金融危机的影响，人民币暂停了升值走势，直到2010年重启冻结的汇率制度，特别是在2012年4月央行加大了汇率波动幅度，由0.5%扩大到1%。种种迹象表明，增强人民币汇率弹性、促进人民币国际化是大势所趋。因此，我国应积极培育汇率市场化的环境及人民币国际化的条件。比如加快产业结构调整，提高我国出口商品的附加值，增强其国际竞争力；鼓励国内资本“走出去”战略，鼓励进口先进设备及高端技术，以减少人民币汇率的持续升值预期；加强汇率衍生市场的建设，规避汇率市场化带来的汇率风险等等。

另一方面，充分考虑汇率波动的集群性、持续性以及杠杆效应，我国现阶段汇率政策的制定仍需谨慎而行。既要根据经济的需求对汇率进行适当的浮动，以缓解人民币的升值压力，又要考虑到汇率波动的集群性、持续性以及杠杆效应，避免波动过度对贸易及国内经济造成的长期负面冲击。在增强人民币汇率弹性的同时仍应综合考虑各个因素加以必要调控，条件未成熟时汇率的波动幅度仍不能过大。

[1] ENGLE R F.Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation[J].Econometrics,1982(50):987-1008.

[2] BOLLERSLEV T.Generalized Autoregressive Conditional Heteroscedasticity[J].Journal of Econometrics,1986(31):307- 327.

[3] ENGLE R F,LILIEN D M,ROBINS R P.Estimating Time Varying Risk Premia in the Term Structure:The ARCH-M model[J].Econometrica,1987(55):391-407.

[4] CHOU R F.Volatility Persistence and Stock Valuations:Some Empirical Evidence Using GARCH[J].Journal of Applied Econometrics,1988(3):279-294.

[5] NELSON D B.Conditional heteroskedasticity in asset returns:A new approach[J].Econometrica,1991(59):347-370.

[6] ZAKOIAN J.Threshold Heteroskedastic Model[J].Journal of Economic Dynamics and Control,1994(18):931-955.

[7] 骆珣,吴建红.基于GARCH模型的人民币汇率波动规律研究[J].数理统计与管理，2009(2):295-300.

[8] 翟爱梅.基于GARCH模型对人民币汇率波动的实证研究[J].技术经济与管理研究,2010(2):20-23.

[9] 常振海,张德生,刘薇.基于小波分析和GARCH模型的人民币汇率实证研究[J].山西大学学报：自然科学版,2009(3):363-366.

[10]夏强,刘金山.基于MCMC算法的人民币汇率市场的分析——双门限非对称GARCH模型的应用[J].数理统计与管理,2012(3):419-425.

[11]孙映宏,曹显兵.基于GARCH模型的中美汇率实证分析[J].数学的实践与认识,2012(20):223-228.

[12]谢非，刘林清.基于GARCH模型的企业汇率风险度量研究[J].重庆理工大学学报：社会科学，2014(6):25-28.

(责任编辑 许若茜)

Dynamic Effects of RMB Exchange Rate Fluctuation Based on High-Frequency Panel Data

YU Ju

(College of Economy & Trade, Chongqing University of Technology, Chongqing 400054, China)

By using the GARCH model based on the high frequency data of 1771 RMB exchange rate during the period of 2006-2013, an empirical study on the fluctuations of RMB exchange rate against USD, HKD, JYP, EUR and GBP was conducted. The results show that: (1) the fluctuations of RMB exchange rate convert five large foreign currency exist ARCH effects, and its earnings show obvious cluster feature; (2) the volatility of the RMB convert five foreign currency exchange rate has a memory, but in addition to HKD and JPY, the memory will show slow decay as time goes by; (3) the fluctuations of the RMB against five foreign currency exchange rate have obvious lever effect, but there are some differences of reaction to RMB appreciation in different foreign currencies.

RMB exchange rate; volatility; GARCH model; high frequency data

2014-10-23 作者简介：余菊(1976—)，女，重庆壁山人，讲师，研究方向：国际金融。

余菊.基于高频面板数据的人民币汇率波动规律研究[J].重庆理工大学学报:社会科学，2015(9):27-33.

format：YU Ju.Dynamic Effects of RMB Exchange Rate Fluctuation Based on High-Frequency Panel Data[J].Journal of Chongqing University of Technology:Social Science，2015(9):27-33.

10.3969/j.issn.1674-8425(s).2015.09.006

F832.6;F752.6

A

1674-8425(2015)09-0027-07