最小二乘法、矩法和最大似然法的应用比较

胡 德，郭刚正

（1.中南财经政法大学 金融学院，武汉 430073；2.华中科技大学 经济学院，武汉 430074）

0 引言

随着统计和计量技术的不断发展和完善，参数估计在研究经济金融问题中发挥着越来越重要的作用，日益成为统计推断和经济预测的基石。参数估计的目的是通过已知样本推断未知总体的分布情况和数字特征，并力求使估计量满足无偏、有效、一致等性质，使估计具有更高的精度。常用的参数估计方法分为三大类：最小二乘法、矩法和最大似然法。其中，最小二乘方法体系的基础是普通最小二乘法，矩方法体系的基础是矩估计法，最大似然方法体系的基础是最大似然估计法。对参数估计方法的研究，必须始于这三种基础方法。

目前，国内外专家学者对参数估计方法做了大量研究，并形成一些高质量的研究成果。现有的研究大致可分为两个方向：其一是研究参数估计方法的构造、推导变换以及求解等方面的问题；其二是研究在解决实际问题时如何灵活、有效地选取参数估计方法。但对于参数估计方法进行多角度、全方位的系统性比较研究相对不足。本文基于这一现状，尝试构建方法特点、适用条件、估计精度等三维比较的研究框架，通过对同类方法做“类之内”的横向对比，对不同类方法做“类之间”的纵向对比，深入认识各参数估计方法的特点，分清各参数估计方法的适用条件，综合比较在既定条件下各参数估计方法的估计精度差异，为通过参数估计方法研究具体经济金融问题提供参考。

1 三大类估计方法特点及适用条件的比较

1.1 三大类估计方法的思想概述及估计量推导

最小二乘法，是以样本观测值与估计值残差平方和最小为标准对未知参数进行估计的一类参数估计方法。普通最小二乘法（OLS）是最小二乘思想最直接的运用，当模型为经典线性回归模型时，普通最小二乘估计量具有非常好的性质与估计精度。当模型误差项存在异方差，通常使用加权最小二乘法（WLS），对每一个平方分项赋予一个适当的权数，保证各项在平方和中的作用相当。若回归模型误差项同时存在异方差和自相关，则一般采用广义最小二乘法（GLS）对误差项协方差矩阵作恒等变换，消除偏误影响。当模型解释变量存在内生性时，两阶段最小二乘法（2SLS）选取合适的工具变量代替原内生解释变量对回归系数作出估计。若解释变量存在严重的共线性问题，参数估计值将会很不稳定，可能影响到显著性检验，甚至造成回归系数正负号的错乱。霍尔在1970年提出的岭回归估计法（RR）通过人为作出不等价变换，改进了估计精度。

矩法，是利用样本矩或样本矩构造的方程来估计总体参数的一类参数估计方法。矩法以矩估计法为基础，主要包括矩估计法和广义矩估计法。矩估计法（MME）旨在用样本矩代替相应总体矩并反解得到参数估计量，需要矩估计方程和待估参数个数相同，方可正好识别待估参数。当估计方程个数多于参数个数或为更精确估计总体参数而选用更多样本矩时，通常采用广义矩估计法（GMM），寻找使样本矩与总体矩离差平方和最小的参数估计量。

最大似然法最早是由德国数学家Gauss在1821年针对正态分布提出的，而Fisher在1922年再次提出这种想法并证明了它的一些性质而使其得到广泛的应用。最大似然法以最大似然原理为思想基础，它认为，在随机抽取出n组样本观测值后，最合理的参数估计量应该是能使抽取这n组样本观测值的概率最大的估计量。最大似然类估计方法一般只包含最大似然估计法（ML），它能全面反映最大似然思想。

针对线性回归模型Y=Xβ+U，最小二乘类估计量的求解，本质上是一个求样本观测值与估计值残差平方和最小的极值问题，矩类估计法利用总体矩对未知参数的反解以及样本矩对总体矩的替代求得估计量，最大似然估计量则是使似然函数达到最大的估计量。表1对三大类参数估计方法估计量结果进行了汇总。

表1 三大类参数估计方法的估计量

1.2 三大类估计方法的特点比较

1.2.1 三大类估计方法的特点总结

最小二乘法、矩法和最大似然法因设计原理迥异而具有不同的特点，每一大类估计方法的若干子方法也在估计条件、估计结果等方面存在较大差异。本文从方法的应用背景、对总体分布要求、对样本量要求、模型满足相应条件下估计量性质、方法灵活性、复杂性等方面着手，比较并总结不同方法的特点。表2是对三大类参数估计方法特点的汇总。

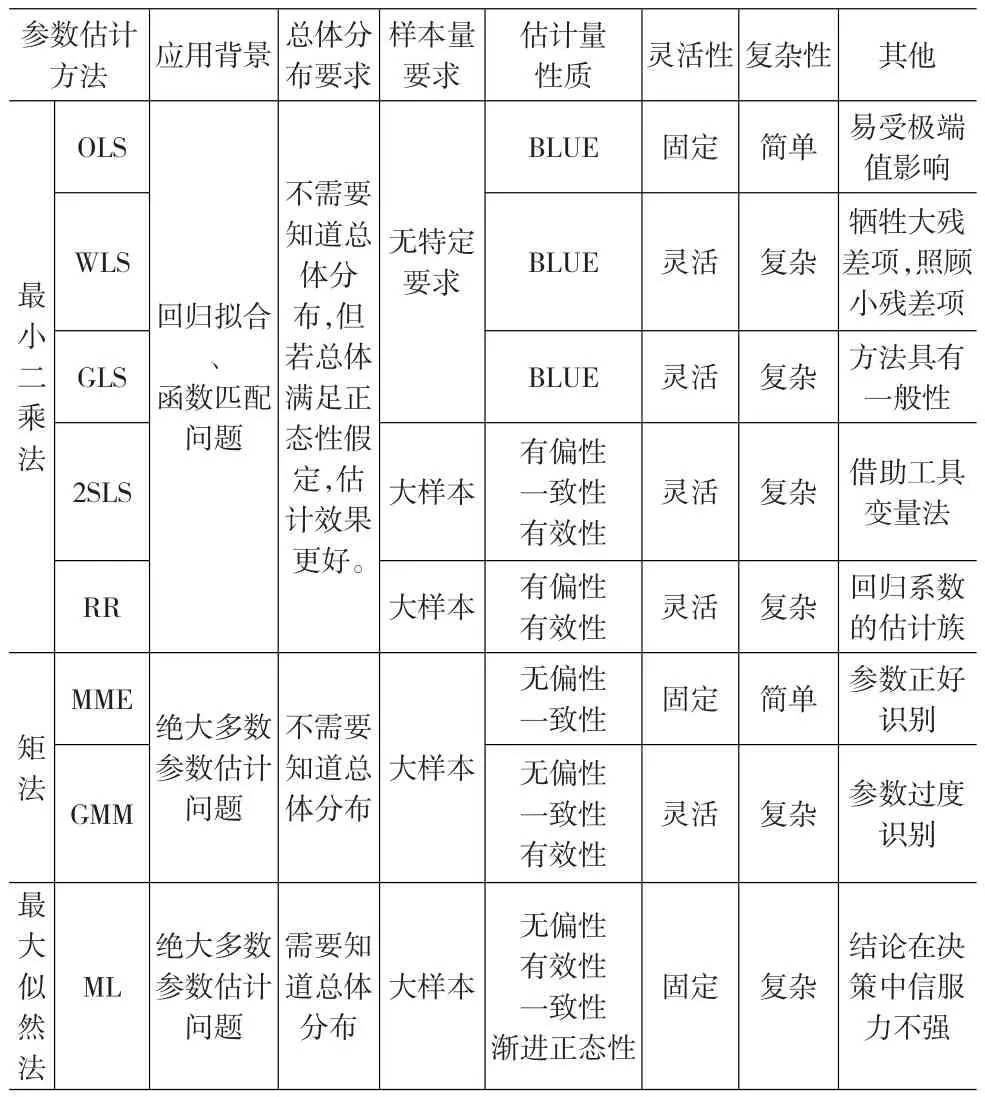
表2 三大类参数估计方法的特点

1.2.2 “类之内”方法的特点比较

（1）最小二乘类估计方法特点比较

①假设条件不同，使用的方法就不同

五种最小二乘估计法的原理是一样的，但在不同假设条件下，会有不同的使用。当回归模型非常理想、满足经典假定时，OLS是最佳方法。当存在误差项异方差、自相关、解释变量内生、严重多重共线性等偏误时，应相应使用WLS、GLS、2SLS、RR方法。

②从过程上讲，OLS是其他四种方法的一部分；从结果来看，OLS是这四种方法的特例

OLS不仅是WLS、GLS、2SLS和RR的思想源头，更是这些方法求解过程的一部分。OLS作为WLS、GLS、2SLS、RR的基础，必然存在一种推广和特例的关系，从估计量结果来看，也印证了这一点。当权矩阵W=I时，WLSE退化为OLSE；当误差项的协方差矩阵分别为Ω=W-1与Ω=I时，GLSE退化为WLSE与OLSE；当工具变量Z等于原内生解释变量Xj时，2SLSE退化为OLSE；当岭参数k=0时，RRE退化为OLSE。

③在各自假设条件下，OLSE、WLSE、GLSE是BLUE，2SLSE有偏但具有一致性，RRE有偏但比OLSE更有效

由高斯—马尔可夫定理可知，模型满足经典假定时，OLSE是BLUE。WLSE和GLSE都是OLSE的等价推导，因此，误差项存在异方差和自相关时，WLSE和GLSE具有BLUE性质。2SLS法选取了外生工具变量替代原有解释变量、岭回归估计法直接改变了OLSE的形式，其估计量也丧失了无偏性。但可以证明，在大样本条件下：2SLSE依概率收敛于回归系数，具有一致性；而岭参数选择合适时，RRE比OLSE的均方误差要小、更有效。

④2SLS、RR要求样本量足够大，OLS、WLS、GLS对样本量无要求

OLSE、WLSE、GLSE具有无偏性，因此OLS、WLS、GLS三种方法对样本容量大小没有要求。2SLSE和RRE是有偏的，只有在大样本条件下才能体现出其一致或有效的优良性质，所以，在使用2SLS和RR方法时，要保证样本容量足够大。

（2）矩类估计方法特点比较

①MME和GMM是同一体系的不同方面

MME和GMM本质上都是用样本矩对总体矩的代替，当样本矩的个数等于未知参数的个数时，需要使用MME，当样本矩的个数大于未知参数的个数时，GMM就体现出独特性和优越性了。因此，MME和GMM是在矩法体系下的两个不同方面。

②MME和GMM的相同点

MME和GMM的设计原理相同，对总体分布与样本容量的要求也相同。就估计量性质而言，MME和GMME都是弱假设条件下的无偏一致估计量。在不知道总体分布的假设条件下，MME和GMME具有无偏性和一致性。同时，MME和GMM两种方法原理简单，理解起来较容易，其计算过程主要是反解和求极值，求解并不太复杂，具有较强的可实施性。

③GMM是MME的深化和改进

首先，GMM的精确程度高于MME。样本矩数量越多，样本的信息量就越大，GMM所利用的样本信息多于MME，其估计精度也更高。其次，GMM的灵活程度高于MME。MME对各项样本矩的地位一视同仁，而忽视了不同矩条件具有不同方差的特点；GMM则考虑了这一因素，通过权矩阵的设置，灵活调配不同矩条件的权重。最后，矩估计法是广义矩估计法的一个特例，广义矩估计量在样本矩个数等于未知参数个数、且权矩阵设为单位矩阵时退化为矩估计量。

1.2.3 “类之间”方法的特点比较

①最小二乘法、矩法和最大似然法对总体分布、样本容量的要求不同

最小二乘法对总体分布和样本容量的要求较松。OLS、WLS、GLS、2SLS以及RR并不要求知晓总体分布的具体形式，只有2SLS和RR需要保证样本容量足够大。矩法和最大似然法一般被用于大样本情况下模型参数的估计，它们在大样本条件下显示出优良的估计性质。使用最大似然分布的前提是已知总体变量的具体分布，而分布的设定难免有人为的因素。矩法不需要对变量的分布进行假定，它只需要找到一些矩条件，而不是整个分布密度函数。因此，在大样本下，矩法的估计结果总是不会偏离很远。当然，矩法对总体分布的要求是以牺牲样本信息量为代价的，MME和GMM有时不能对全部样本信息进行有效利用。

②最小二乘估计量、矩估计量和最大似然估计量的性质差异

在各自的适用条件下，每种方法都能发挥其特点，得到合适的估计量。不同的条件下，无法将每一类估计量作出直接比较。本文试图探讨这些参数估计量在满足各自估计方法适用条件时的性质差异，以完成纵向对比。

OLSE、WLSE、GLSE以及MME、GMME、MLE都具有无偏性，这意味着这六类参数估计量都是紧紧围绕总体参数而进行估计的。2SLS和RRE是有偏的，它们必须从其他性质上对有偏性作出弥补。

一致性和有效性也是评判估计量是否准确的重要性质。在大样本条件下，OLSE、WLSE、GLSE、2SLSE、MME、GMME、MLE都能保证一致趋于总体参数，OLSE、WLSE、GLSE、RRE、GMME、MLE都被证明具有最有效性。它们是各自适用条件下的优先考虑。

OLS、WLS、GLS可以适用于小样本数据，它们在小样本条件下也具有很好的估计性质。满足经典假定下的OLSE、存在异方差下的WLSE、同时存在异方差和自相关下的GLSE，都是最佳线性无偏估计量。

③最小二乘法和最大似然法是广义矩估计法的特例

广义矩估计法是一种高度概括的方法，其他很多参数估计方法都可以看作它的特例。最小二乘法和最大似然法，以及矩估计法就是GMM的特例，这是因为：

当GMM的权矩阵为单位矩阵时，GMM即为OLS；

用对数似然函数导数等于0的条件作为矩条件时，GMM即为ML；

与MME相比，GMM的使用场合是估计方程个数大于未知参数个数，当两者相等时，即退化为MME；

WLS、GLS、2SLS、RR都是OLS的推广，因而也都是GMM的特例。

从适用范围来看，也可以说明最小二乘法和最大似然法是广义矩估计法的特例。最小二乘法主要适用于回归拟合与函数匹配的参数估计问题，这属于矩法估计的范围之一；最大似然法要求总体分布已知，而矩法则弱化了这一要求，前者的适用范围包含于后者。

1.3 三大类估计方法的适用条件总结

参数估计方法的好坏很大程度上取决于待解决的问题是否满足方法的适用条件。选择合适的估计方法会降低估计难度，改善估计量性质，提高估计精度。因此，有必要对三大类参数估计方法的适用条件进行比较研究。

确定估计方法适用条件的准则一般有三点：是否需要知道总体分布、是否对样本量大小有要求、满足什么假设条件下估计量性质最好。本文结合最小二乘法、矩法、最大似然法这三大类参数估计方法的原理、实施过程以及特点，对其适用条件作出描述和比较。表3是对三大类参数估计方法适用条件的汇总。

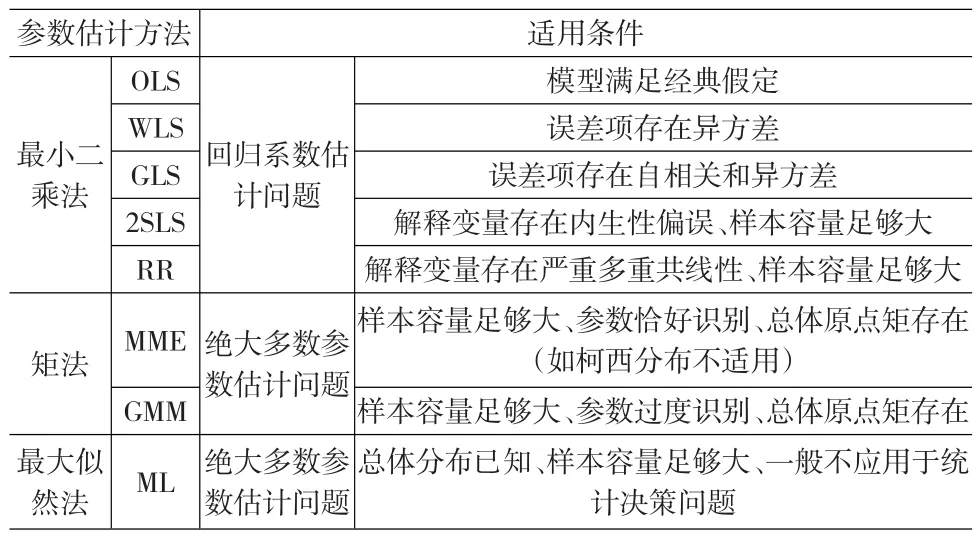
表3 三大类参数估计方法的适用条件

2 基于具体经济金融问题的实证比较

2.1 模型的建立与估计

为论证上述比较研究的实效性，本文立足具体经济金融问题，构建多元回归模型，利用各种参数估计方法估计模型的回归系数，并比较不同估计值的估计精度。

2.1.1 经济理论阐述及模型选取

2006年，吴敬琏在《经济增长模式与技术进步》一文中指出，我国经济增长的问题主要是增长模式的问题，表现为依靠大量的能源消费来实现经济增长。宏观经济理论认为消费随生产、收入、通货膨胀、进出口等因素变化，而GDP、财政收入、货币供应量、货物进出口总额四个变量能很好地反映生产、收入、通货膨胀、进出口这四个因素。因此，本文实证模型的被解释变量选取能源消费总量，解释变量选取GDP、财政收入、货币供应量和货物进出口总额。

记我国能源消费总量为变量Y，GDP为变量X1，财政收入为变量X2，货币供应量为变量X3，货物进出口总额为变量X4。变量数据来源于《中国统计年鉴》，采用的样本是1990-2013年度能源消费总量、GDP、财政收入、货币供应量、货物进出口总额等五个变量的数据。样本取自1990年是出于数据选取可行性的考虑，中国统计年鉴拥有这五个变量的完整数据仅从1990年开始。样本量为24个，属于中等样本，可能会对某些估计量的性质存在一定的影响，但无碍于对估计精度差异的分析。根据所得数据作出各变量数据的趋势图：

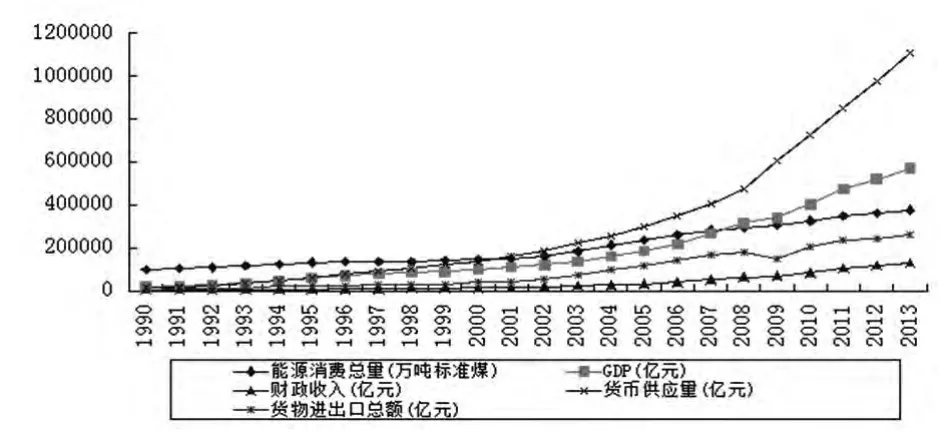
图1 1990-2013年能源消费总量、GDP、财政收入、货币供应量、货物进出口总额趋势图

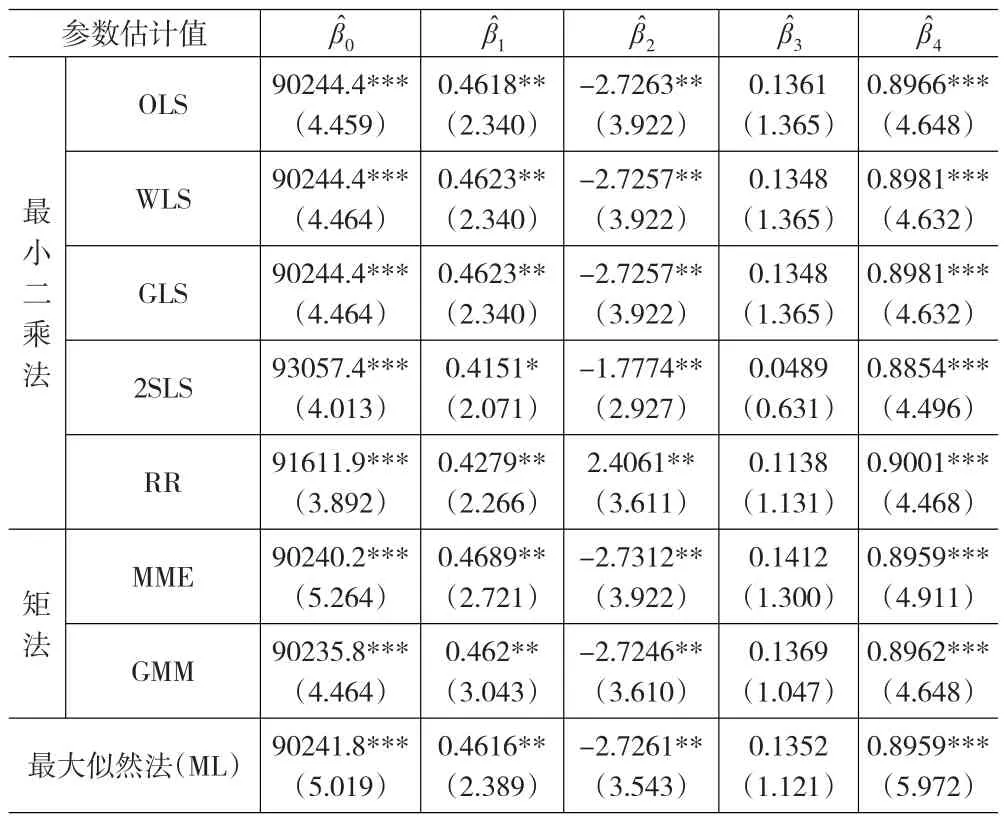
表4 回归模型系数的估计值

从图1可以看出，这五个变量基本趋势都是逐年增长的，其中货币供应量的增长幅度最大，GDP的增长幅度次之，能源消费总量、货物进出口总额和财政收入基本呈现直线型增长。图中趋势线表明：GDP、财政收入、货币供应量、货物进出口总额这四个解释变量的回归系数符号均为正。

因此，可建立线性回归模型：Yi=β0+β1Xi1+β2Xi2+β3Xi3+β4Xi4+ui，i=1，2，…，24，分别使用OLS、WLS、GLS、2SLS、RR、MME、GMM、ML，估计回归系数，得到变量之间的关系。

需要说明的是：对于财政收入这个内生性很强的解释变量（其与误差项的相关系数达到0.99），选取城镇居民人均可支配收入（与财政收入相关系数达0.99，与误差项相关系数仅为0.36）作为工具变量，使用两阶段最小二乘法估计参数。

2.1.2 估计结果

使用EViews7.0软件和Stata12.0软件对回归系数作估计，求得不同参数估计方法下的估计值，其结果见表4。

从估计结果来看，OLSE、WLSE、GLSE、MME、GMM以及MLE相差不大，它们都围绕在参数真实值附近浮动，是总体参数的无偏估计。解释变量中，货币供应量对能源消费总量的影响最小，货币供应量每增加一个单位，能源消费总量增加约0.135-0.141个单位；财政收入对能源消费总量的影响最为明显，且是负影响，财政收入增加一个单位，能源消费总量减少至少2.724个单位。而从图1各变量散点图以及变量之间的相关系数来看，财政收入与能源消费总量之间应该是正向影响，这可能是由于变量之间存在严重多重共线性导致的回归系数符号与实际意义不符。

2SLSE和RRE结果与前三种估计方法结果有明显差别，原因在于它们是回归系数的有偏估计。2SLS和RR所得结果依然说明了货币供应量对能源消费总量的影响最小，财政收入对能源消费总量的影响最大。RR下财政收入变量的回归系数为正，岭回归估计对多重共线性的修正具有很好的效果。

此外，在5%的显著性水平下，财政收入变量和货物进出口总额变量在回归模型中严格显著，GDP变量也基本达到显著水平，但货币供应量变量在显著性方面存在一些不足。

2.1.3 模型假设条件检验

估计方法的优劣取决于该方法是否适用于特定模型的条件。选用一种估计方法，首先要看实际问题符合什么假设条件，不同的假设条件需要采用不同的估计方法。文章借助EViews7.0软件对回归模型的经典假定条件作出检验。

White检验结果表明模型存在微弱的异方差偏误，拉格朗日乘数检验结果表明模型不存在自相关偏误，财政收入变量与随机误差项之间相关系数达到0.99，说明模型存在解释变量内生性偏误，而方差扩大因子计算结果则显示模型存在严重的多重共线性。

因此，建立的回归模型是一个存在微弱异方差、无自相关、解释变量具有内生性和严重多重共线性的回归模型。理论上，三大类参数估计方法对这一模型系数的估计精度具有较大差异。

2.2 估计精度比较

2.2.1 估计精度的度量及其结果

计算估计精度一般有两种思路。第一种思路是将估计值与样本实际值作差，构造均方误差MSE、绝对误差MAE等指标，以估计值离实际值最近为标准判断估计精度高低。但这种方法在这里存在一些问题。因为OLS原理就是残差平方和最小，与MSE、MAE等指标的本质相同，无法作出准确的精度比较。第二种思路借用区间估计的思想，以估计值的标准误作为判断估计精度高低的依据，标准误越小，估计值的精度越大。本文选用第二种思路。

本文计算出不同参数估计方法下回归模型系数估计值的标准误，结果见表5。

2.2.2 “类之内”方法的估计精度比较

（1）最小二乘类估计方法精度比较

由表5可得：RR的估计精度最高，2SLS的精度次之。WLS和GLS的精度大致相当，要低于2SLS，而稍稍高于OLS。

因此，对存在微弱异方差、无自相关、解释变量具有内生性和严重多重共线性的回归模型进行参数估计，应优先选用RR和2SLS。

实证结论验证了最小二乘类估计方法特点及适用条件比较研究的理论。依据已建立的理论，在模型条件发生改变时，不同方法估计精度的高低也会相应变化。

对于不存在解释变量内生性偏误和严重多重共线性偏误的回归模型，可以推断出：OLS、WLS、GLS的估计精度较高，不低于2SLS和RR的精度。

对于不存在解释变量内生性偏误和严重多重共线性偏误的回归模型，若模型误差项存在自相关和异方差，则能够推断出：GLS的精度最高，WLS的精度次之，OLS的精度低于前两者，不低于2SLS和RR的精度。

（2）矩类估计方法精度比较

通过对表5结果的比较可得：对于存在微弱异方差、无自相关、解释变量具有内生性和严重多重共线性偏误的回归模型，GMM的精度较MME更高。这一精度比较的结论可由MME和GMM的构造与求解过程加以解释：GMM比MME利用了更多的样本信息，前者对总体参数的估计精度更高。对于满足其他假设条件的回归模型，GMM精度高于MME精度的结论一般也是成立的。

2.2.3 “类之间”方法的估计精度比较

在模型存在微弱异方差、无自相关、解释变量具有内生性和严重多重共线性的情况下，观察表4和表5，能够发现以下结论：

OLS、WLS、GLS、MME、GMM、ML这六种方法的估计值结果相差不大，而2SLS和RR的估计值结果与前六种方法有较大差别。这是因为，OLSE、WLSE、GLSE、MME、GMME、MLE都具有无偏性，它们的估计值基本围绕在真实值附近；2SLSE和RRE因为构造过程中的不等价变换，丧失其无偏性，所得估计结果与真实值存在一定差距。

从各大类估计方法中精度最高的子方法比较的角度来看，RR精度最高，GMM精度次之，ML精度最低。这是因为，最小二乘法是为回归拟合问题而设计，RR更是解决了严重多重共线性问题，因此其估计精度最高；GMM不需要知道总体分布情况，所得到的结果一般不会偏离总体很远；ML需要知道总体具体分布才能进行有效的参数估计，容易出现较大偏误。

从OLS、MME、ML这三种基本方法比较的角度来看，OLS的估计精度最高，MME精度次之，ML精度最低。

可见，在研究经济金融问题中，面对存在微弱异方差、无自相关、解释变量具有内生性和严重多重共线性的回归模型，最小二乘法是最合适的参数估计方法，矩法稍劣于最小二乘法，而一般不使用最大似然法。

[1]茆诗松,程依明,濮晓龙.概率论与数理统计[M].北京:高等教育出版社,2011.

[2]易丹辉.数据分析与EViews应用[M].北京:中国统计出版社,2002.

[3]高鸿业.宏观经济学[M].北京:中国人民大学出版社,2011.

[4]吴敬琏.经济增长模式与技术进步[J].中国科技产业,2006,（1）.

[5]Fisher R A.On the Mathematical Foundation of Theoretical Statistics[J].Proc.Camb.Soc.,1925,（22）.

[6]Larsen R J,Marx M L.An Introduction to Mathematical Statistics and its Application[M].New Jersey:Prentile-Hall,1986.

[7]Hansen L P.Large Sample Properties of Generalized Method of Moments Estimators[J].The Econometric Society,1982,50(4).