基于GARCH族模型的收益波动率预测绩效评估方法

刘 青，戴经跃,杨 超

（1.辽宁师范大学 数学学院，辽宁 大连116029；2辽宁税务高等专科学校 计统系，辽宁 大连 116023）

0 引言

波动率是金融经济研究中的一个非常重要的变量，在金融市场中，无论是金融产品的投资组合、风险管理还是资产定价，波动率都扮演着非常关键的角色。如何对金融资产的收益波动率进行精确的描绘与预测是金融学领域关注的焦点之一。分析收益波动率的特性及走向，对投资者度量和规避市场风险均有重要的研究价值和实际意义。本文采用半参数方法估计GARCH族模型，并进行样本外的一步外推（One-Step-Ahead）预测。EF方法在估计的过程中引入了收益率的偏斜和峰度信息，其估计结果比QMLE更高效。此外，与参数化的条件分布相比，EF方法不受限于具体的分布模式，这样尽可能地降低了“模型风险”。EF方法与广义矩估计（GMM）较为相似。不同之处在于，EF方法所使用的估计函数相当于GMM中的正交化处理功能，并依照一定的规则优化后的“矩条件”，其效率也高于GMM。本研究将分别采用这两种方法进行估计和预测。此外，为了减少绩效评估的“数据窥察”问题，给出统计意义下的结果，本文将采用最小二乘（OLS）方法进行模型绩效对比。最后，检验结果发现，EGARCH模型能提供较为优越的预测效果。

1 GARCH族结构与参数估计

1.1 GARCH族结构描述

假定资产的收益率时间序列rt服从随机分布rt|Ψt-1~D(μt，ht)，其中 Ψt-1为 t时刻的已知序列集。为了规避时间序列在1阶矩上的自相关信息误入2阶矩，引入以下模型，

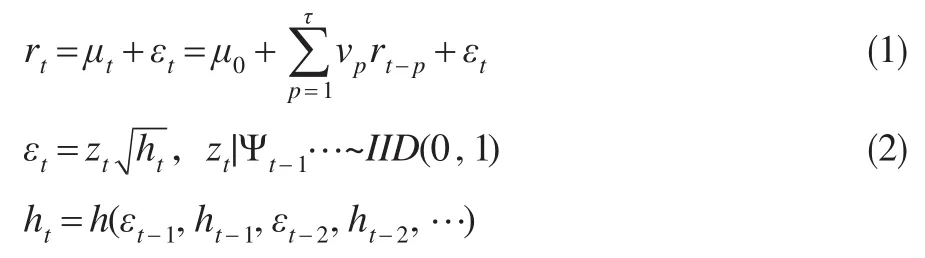
这里，截矩项μ0和滞后阶数τ分别根据回归的显著性、残差的Q统计量以及AIC信息准则决定；εt表示扰动项，基准扰动项zt条件在以往的信息上服从0均值单位方差的独立同分布；ht=h(εt-1，ht-1，εt-2，ht-2，…)表示方差方程。每类GARCH族结构均根据一定的经验发现并对h(·)作的不同变换。例如较常见的GARCH(1，1)模型，具有形式精简、可理解的特点，基本形式如下式所示：

实际的波动曲线通常表现出较好的连续性，相关研究者提出了积分GARCH（IGARCH）：

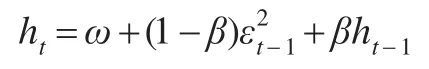
此外，为了描述波动过程的非对称性波动，采用较广泛的指数型GARCH（EGARCH）：

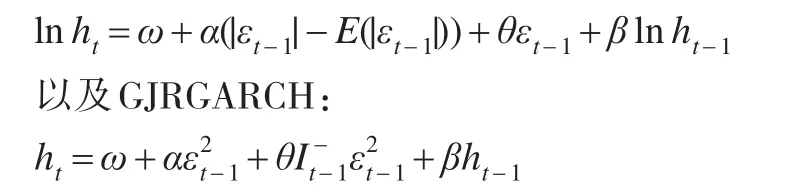
从以上的模型构建中不难看出，一些模型之间存在相互重叠关系，例如GJRGARCH、AGARCH等都嵌套了GARCH基本模型。尽管模型之间存在较多的嵌套关系，但将这些被嵌套的模型纳入“模型全集”有利于发现更加精简的形式。这是由于若嵌套模型对被嵌套模型进行推广，从波动率预测的视角来说并不必要，这样，被嵌套的结构的参数估计将更为高效，继而表现出更加有效的预测性能。

1.2 基于EF的参数估计策略

在传统的GARCH族模型中，通常采用高斯分布下的极大似然法进行参数估计。由于金融资产的收益率曲线常显示出偏斜和超额峰度特性。此时，QMLE尽管理论上仍能保持渐近一致性，但估计的效率较差。实际应用中，通常会综合考虑预测的无偏性和效率性对模型的预测绩效进行评估，如常用的“均方误差”（MSE）指标。因此，QMLE方法在估计不同的模型时出现的效率代价，可能会改变MSE等指标对模型预测绩效的评估结果。这就有必要采用比QMLE更为有效的参数估计方法。

由于在假定概率密度函数已知时，完全的参数化方法存在潜在的模型风险，因此，本研究将引入一种半参数方法——估计函数法EF，并将其应用到上述各族GARCH模型。此时，估计函数与GMM法中的矩条件较为类似，即找到一个连续可微的函数式 f(·)满足下式

这里 Θ=(θ1，θ2)，θ1与 θ2分别是均值方程与方差方程中的参数序列；另外，Θ对应于随机过程{rt|t=1，2，…，T}相应的概率空间。为了方便描述，不考虑条件信息集Ψt-1，并用Et(·)代表条件期望的计算函数。满足式（5）的函数 f(·)称之为正则函数。但与GMM方法中的矩条件具有差异性的是 f(·)满足另一条件，即对∀Θ=(θ1，θ2)，如下所示的Q 值均达到最小值，

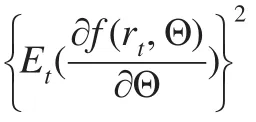
GARCH族模型中的正则函数可表示为如下：

2 一步外推预测与绩效评估方法

2.1 滑动窗口的一步外推预测

为了避免过拟合问题，将{rt|t=1，2，…，T}划分为T=S+F两部分构成。这样，将总体样本更新为{rt|t=-S+1，-S+2，…，0，1，2，…，F}，待预测的时间序列为{ht|t=1，2，…，F}。采用滑动窗口的1步外推预测策略如下：（1）构建样本估计模型{rt|t=-S+1，-S+2，…，0}，并预测 h1；（2）利用样本{rt|t=-S+2，-S+3，…，1}预测 h2；根据以上步骤，在第k步，预测hk时所采用的样本为{rt|t=-S+1+k，-S+2+k，…，k-1}，k=1，2，…，F 。 采用滑动窗口的一步预测法可允许训练信息在模型中得以利用，还能提高模型在结构变化时的参数适应性。

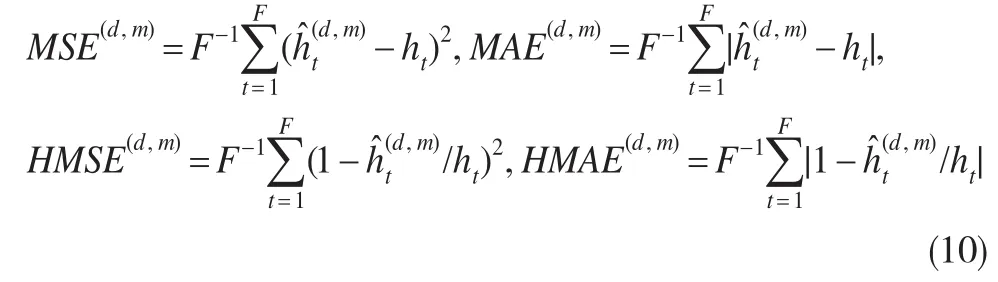
这四种代价函数均为衡量模型预测的无偏性和效率性的有效指标，但不同的代价函数对异常点（Outlier）的敏感程度却有所不同。因此，本研究将分别使用这四种代价函数对GARCH族结构的波动性预测绩效进行测量。

2.2 预测的绩效评估

2.2.1 已实现波动率

本文的研究将以“日”作为收益率的采样周期。由于单日内的实际波动通常难以发现，因此我们以“已实现”波动作为替代变量，表示如下：

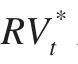
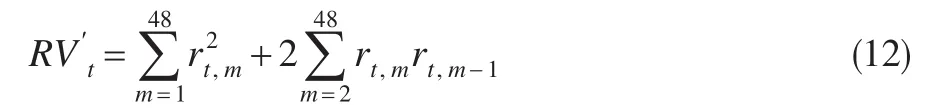
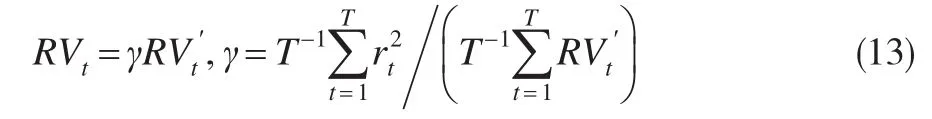
上式中，T表示一天内的样本数量。不同于以往对代价函数的排序策略，本文将使用最小二乘（OLS）机制对6种GARCH族模型，分别利用QMLE和EF为参数策略时，四种预测的代价函数的差异进行对比和统计检验。

2.2.2 绩效评估的最小二乘（OLS）检验

其中，截距c为模型m*与m分别采用d*和d作为参数估计策略时，代价函数的差异值。所以，截距c表示模型m*和m分别以d*和d为参数估计策略的相对代价；其中，m*，m=0，1，2，…，9 ，且 m*≠m ；d*，d=0，1。由于扰动项ξt存在潜在异方差和自相关现象，为了计算c的具有无偏性的标准误差，拟合时采用NW方法进行微调。因此，如果c^显著小于0，则表明标准模型m*以d*为参数时的预测性能显著优于备选模型m以d为参数时的预测性能，反之则反。

3 实证研究

3.1 样本描述

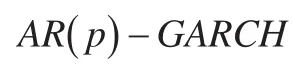
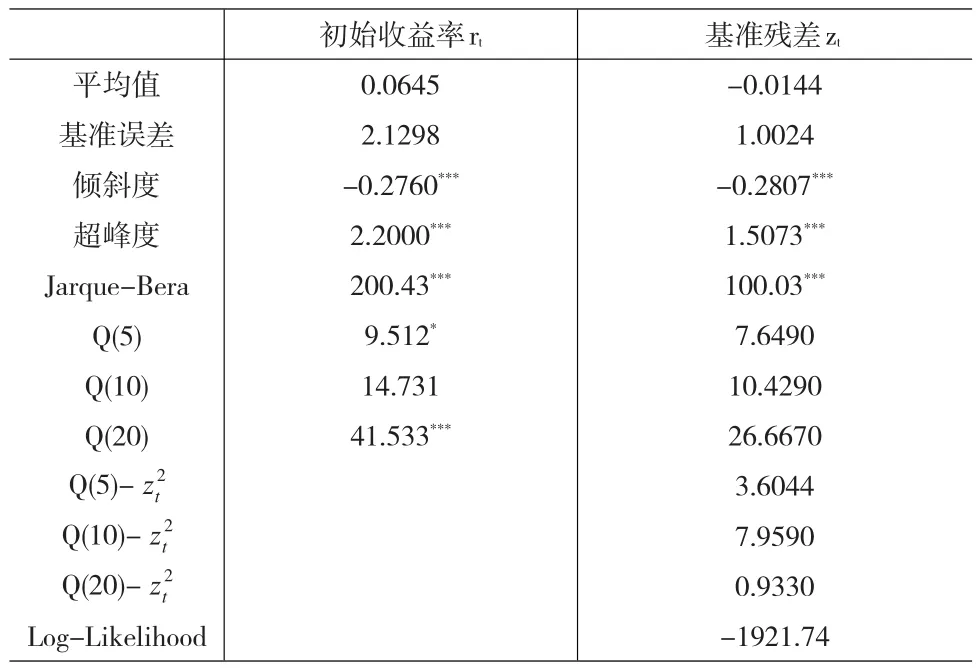
表1 上证综指的初始收益率以及经AR(p)-GARCH拟合后的基准残差的统计结果

表1中的统计量表明，由AR()p-GARCH拟合后，基准残差的1阶和2阶矩上的自相关已基本抵消，意味着拟合后的基准残差可等价于白噪声过程。尽管如此，两市的指数收益均有显著的负倾斜度和超额峰度值，并且采用Jarque-Bera假设检验时，高斯模型被显著拒绝了。这样，描述性统计结果已初步表明高斯分布并不适合代表样本数据的分布。

3.2 分析结果

研究中每种GARCH模型均采取滑动窗口的一步预测。将934天的最后100天作为外部观察值。为了与现有的研究方法进行对比，我们也将高斯分布作为GARCH族模型的条件分布并作一步预测。表2显示了4种代价函数下，6种GARCH结构的预测绩效。图1以柱状图的方式，直观地显示了4种代价函数下，各种GARCH结构的预测性能。

表2 高斯分布假设下GARCH族模型的波动率预测绩效结果

图1 基于QMLE方法的GARCH族模型的波动率预测绩效

结合表2和图1可观察到，在高斯分布的假设下，采取QMLE估计策略来预测时，IGARCH是GARCH族模型中预测绩效更好的一种异方差模式。然而，如图2所示，基于EF方法的波动率预测结果与图1所示结果具有一些差异。

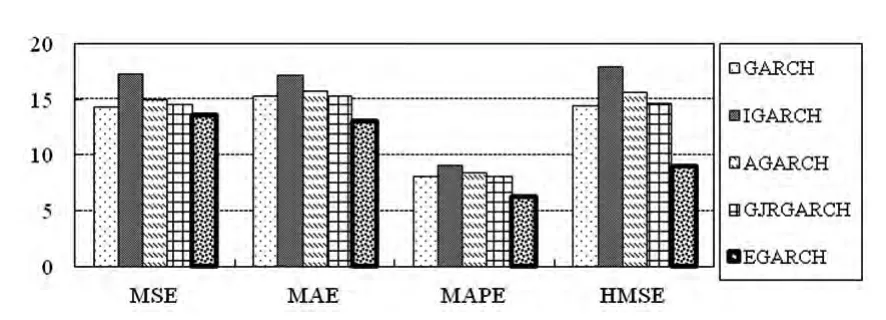
图2 基于EF方法的GARCH族模型的波动率预测绩效

根据图2中的结果，我们发现，采用MSE和MAE为评估指标时，IGARCH和AGARCH是较好的两种异方差模式，而MAPE和HMSE的结果显示，EGARCH模型的预测误差相对较低。此外，与图1对比，基于EF的波动率预测结果显示各类GARCH结构的预测结果差异较大。这说明，QMLE方法在估计模型时存在的效率代价，使得各类模型的绩效差异不会太大，即使最简练的模型仍可呈现出最优的性能；而较为复杂的结构可能需要更加有效的估计策略，才可解释其结构对数据特性的描述力。最终，图2中的4种代价函数均表明，IGARCH结构是表现出较差的绩效。为此，我们进一步考察采用OLS方法来对比各类GARCH结构基于QMLE和EF策略的预测性能，相关结果如表3所示。

表3 各类GARCH结构分别基于EF（基准模型）和QMLE方法的预测绩效比较结果

表3中，方括号中数值代表基于EF方法的预测绩效比QMLE方法提高的百分比，我们可观察到，与QMLE方法相比，IGARCH结构在基于EF方法时的预测绩效并未表现出较好的优越性。前两种结构甚至显著拒绝了EF方法的效果。除此之外的其它7种结构均显示，EF方法与QMLE方法相比，可改善模型的预测性能。特别地，应用EF方法可以显著改进EGARCH模型的预测性能。但由于EF方法引入了倾斜度和峰度等高阶矩信息，因此，在模型确定可精确描绘收益率波动时，EF策略将有可能提高模型的预测性能。相反，如果模型设置错误，采用更为高效的EF策略也会进一步降低模型的预测性能。所以，根据表3的结果，相对于IGARCH结构，选取其它5种设定将更为合适。

图3 QMLE和EF方法下预测绩效好的GARCH族模型比较

为了进一步对不同的估计方法进行对比，我们将在IGARCH模型中使用QMLE策略的预测性能，以及在EGARCH结构中采取EF方法的预测绩效加入同一个对比空间中。从图3可以看出，采用EF方法预测中，性能较高的三种异方差结构均优于两种QMLE方法预测性能高的模型。

综上所述，与其它GARCH结构相比，EGARCH模型可更好对收益率的波动特性进行描述，具有较强的预测性能。此外，由图2或图3可发现，采用MSE和MAE作为度量指标，IGARCH的预测性能将高于EGARCH；但以MAPE和HMSE作为指标时，则不尽然。利用OLS策略将MAPE和HMSE的预测绩效作对比，我们发现4种代价函数的相对绩效并无显著差异，回归检验的p值分别达到0.324（MSE）、0.716（MAE）、0.430（MAPE）和0.362（HMSE），均高于显著性水平0.02。因此，可认为EGARCH和IGARCH模型的预测性能并无明显差异性。

4 结论

本研究从波动性预测的视角，采用一种半参数方法——估计函数策略进行参数估计。由于金融资产的收益率往往呈现出显著的倾斜性和超额峰度，估计函数策略在进行参数估计时加入了一些高阶矩信息，使得比QMLE的估计更为高效。另外，在进行绩效评估时，传统的代价函数排序法难以提供统计意义下的检验结果，且可能存在“数据窥察”问题，本文采用最小二乘（OLS）方法对预测模型进行检验。实证分析结果表明，在高斯分布的条件下，形式最精简的积分GARCH（IGARCH）模型具有较优的预测性能。尽管如此，基于EF策略的预测结果表明，指数GARCH（EGARCH）的预测能力更为优越。主要是因为EF策略具有更佳的估计效率，因此，与其它GARCH类模型相比，本文得出EGARCH模型可更好地描述金融资产收益率的波动过程。

[1]林德钦.创业板指数波动率预测效果比较研究——基于GARCH族模型[J].金融教学与研究,2014,(1).

[2]王鹏，吕永健.基于不同记忆性异方差模型的中国股票市场波动率预测[J].中国管理科学,2013,(S1).

[3]吴晓雄.我国燃油期货市场的波动率预测模型[J].统计与决策,2013,(14).

[4]杨科，田凤平.农产品期货市场波动率的动态特征及其预测模型[J].经济评论,2014,(4).

[5]周伟峰，向华.权证和其标的资产波动率的相关性分析[J].重庆工商大学学报(自然科学版),2014,(1).

[6]杨继平，袁璐，张春会.基于结构转换非参数GARCH模型的VaR估计[J].管理科学学报,2014,(2).

[7]高艳超.GARCH模型、非参数GARCH模型及SV模型的比较综述[J].现代商业,2012,(29).

[8]方立兵，郭炳伸，曾勇.GARCH族模型的预测能力比较:一种半参数方法[J].数量经济技术经济研究,2010,(4).

[9]李翠霞，郭二林，包美娟.一种带有自权重的积分波动率的非参估计[J].中山大学学报(自然科学版),2013,(1).

[10]房小定.基于GARCH族模型族的创业板指数波动性研究[J].金融经济,2014,(8).