人口预测方法的现状、问题与改进对策

沈 巍，宋玉坤

(华北电力大学 经济与管理学院，北京 102206)

0 引言

如何找到符合不同国家或地区人口增长特点的预测方法，构建恰当的预测模型，准确有效的预测出一个国家或地区的未来人口数量及其变化趋势，为决策机构提供有价值的决策依据，最终达到合理控制人口、有效利用资源、科学有序的进行城市规划及环境保护等目的，就显得十分必要和迫切，并具有重要的理论意义和现实意义。为此，国内外众多的专家学者在人口预测领域进行了深入的研究，取得了丰硕的成果。本文以人口预测模型的发展为脉络，对国内外人口预测方法的现状、趋势进行了分析。在此基础上，结合我国人口预测的实际情况，对我国人口预测中存在的各种问题进行了深入探讨，并提出了相应的改进建议。

1 西方传统的基于统计学原理的人口预测方法

1.1 指数模型

1789年，英国人口学家和政治经济学家马尔萨斯在其代表作《人口论》[1]中提出了著名的指数模型，即在没有任何限制的情况下，人口会呈现出指数式增长的特性：

其中，xt表示一段时间t后的人口数量，x0表示初始人口数量，t表示时间，r表示人口增长率。

这是一种理想的人口增长状态，在短期人口相对较少，资源相对充足时，人口有可能会出现类似于指数增长的特性。但现实生活中影响人口数量变化的因素很多，诸如贫困人口迁移、国家政策等等，因而，长期人口数量并不一定会呈现出指数增长的趋势。

1.2 Logistic人口增长模型

19世纪中期，荷兰生物学家费尔哈斯在研究昆虫种群数量变化时发现，在种群规模较小时，环境相对宽松，资源相对充裕，昆虫数量增长会快些；当种群规模达到一定程度后，环境和资源就会显得相对不足，制约着种群中昆虫数量的增长。而人类社会也一样，由于受到政治、经济、自然环境等各方面的制约，人口规模的变化也会存在类似的现象。由此，他在马尔萨斯模型的基础上，考虑进了环境和资源对人口数量的约束作用，提出了一个关于人口规模、人口增长率和环境承载力之间关系的公式，即Logistic公式[2]：

其中，N（t）表示t时刻的人口数量，r表示人口的内在增长率，K表示环境对人口的最大承载力。

在这种模型中，人口增长率是人口的函数，随人口增加而变小，人口增长最后将趋于平缓；而在实际计算中，先将这种非线性模型线性化，然后利用最易计算的线性方程进行求解，其结果为：

其中，N（t）表示t时刻的人口数量，K表示环境对人口的最大承载力，C取决于初始状态N(0)，且

作为一种指数预测模型，Logistic人口增长模型和马尔萨斯指数模型都是以过去某一年的人口数作为基数，通过引入固定的人口增长率来预测某一封闭环境下（即不考虑人口迁移因素）的未来人口数量。但在实际应用中，这种模型还存在着以下不足：（1）人口增长率是变化的，每一年都可能不同，用统一的人口增长率来预测未来多年的人口数量显然是有误差的：（2）人口是在不断流动的，人口迁移因素对一个国家或地区人口数量的影响往往是非常大的，模型中未能考虑到这一点：（3）模型中所要求的环境对人口的最大承载力是很难计算的，会存在较大误差。所以这也只是一种近似算法，并不能准确把握人口增长的趋势，尤其是在人口出现负增长时，这一模型更是无法预测。

1.3 马尔科夫链模型

20世纪初，苏联著名数学家安德烈·马尔科夫在对概率论的研究中，经过多次试验观察发现，系统在状态转换过程中，存在着转移概率，这种概率只与当前转换紧接的前一次有关，而与过去无关[3，4]：

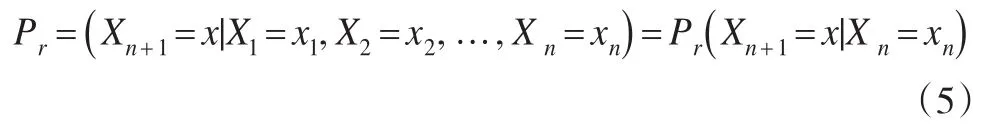
其中，Pr表示转移概率；x1，x2，…，xn表示一系列的随机变量，这些随机变量的可能取值所形成的可列集就叫做马尔科夫链的状态空间。这也是最简单的马尔科夫模型。

马尔科夫链模型在预测中不需要考虑当前以前的历史状态，而是利用当前的状态，通过转移概率来进行预测。因而，将这种模型引入人口预测领域，就可以利用短期少量的人口数据来对未来人口数量进行有效的预测，操作简便易行，尤其是在历史人口数据不全或者不准确的情况下，这种无需考虑历史数据的预测方法就拥有更大的优势。但事实上，转移概率会随时间而不断变化，难以准确计算，马尔科夫模型在实际应用中就可能会产生较大的误差。

1.4 凯菲茨矩阵模型

美国著名人口统计学家内森·凯菲茨率先提出了利用矩阵乘法进行人口预测的想法，建立了矩阵模型。这种方法的基本理念就是将人口按性别、年龄、生育率和存活率分别进行处理，建立矩阵，然后利用矩阵乘法的相关原理进行计算，预测未来人口的发展趋势。其基本模型是[5]：

其中，I表示预测年度人口数量的年龄结构矩阵，M为以预测的年龄组数为阶数的、由生育率和存活率构成的矩阵，K表示不同年龄下的预测基年的人口数。

在其代表性著作《应用数理统计学》[6]中详细阐述了这种预测方法的理念及其应用。

作为一种新的预测模型，矩阵模型在实际操作中考虑到了包括年龄结构、生育率、存活率等在内的更多的因素，更加全面，而且还能具体的预测未来人口的年龄结构，相对于以往的预测模型，有很大的进步。

1.5 莱斯利矩阵

20世纪中期，种群生物学家帕特里克·h·莱斯利在研究中发现，种群的数量与种群的年龄结构之间存在着巨大的关系。为此，他于1945年在对凯菲茨矩阵模型进行改进的基础上，加入了人口迁移因素，提出了基于年龄结构的莱斯利矩阵，并据此建立了莱斯利矩阵模型。其基本表达式为[7]：

式中，P(t+1)表示第t+1年的人口数，A表示基于不同年龄结构下的生育率与存活率矩阵，Pt表示第t年的人口数，Gt表示第t年的人口净迁移数。

这种模型通过将种群划分为不同的年龄层，并考虑到了人口的迁移因素，动态的预测种群的年龄结构及其数量的变化，相对于原始的凯菲茨矩阵而言，有了很大的改善，成为人口预测领域经常使用的一种模型[8]。

但是，作为矩阵模型，凯菲茨矩阵和莱斯利矩阵模型共有的不足之处是：（1）需要通过层层计算来获得数据，然后整体带入，计算较复杂；（2）对数据的要求较高，某一数据的变化或者偏差会对整个结果产生较大的影响；（3）对于那些对人口数量变化有较大影响的经济性因素和政策性因素没有加以考虑。因此，当一个国家或地区的人口数据不是很全面、准确，或者人口变化受经济和政策性影响较大时，运用矩阵模型进行预测就会产生较大的预测误差。

1.6 自回归滑动平均模型

1951年，新西兰著名统计学家彼得·惠特尔在其著《时间序列中的假设检验》一书中，首次尝试将自回归模型（简称AR模型）与滑动平均模型（简称MA模型）联立起来，提出了著名的自回归滑动平均模型(ARMA模型)，这种模型简便易行，计算方便，成为研究时间序列模型的重要方法[9]。随后，该模型被引入人口预测领域，在短期人口预测方面取得了不错的效果，得到了广泛应用。但由于该模型属于线性模型，而人口的增长不一定是线性的，尤其是对于长期人口增长而言，更不可能表现出线性增长的特性，因此，在进行长期人口预测时，该模型会出现较大偏差。

以上6个是被普遍认可和广泛应用的、基于统计学原理的人口预测模型。这类模型均采用严格的数学公式进行预测，逻辑性较强，模型结构较为稳定，易于操作，计算相对简单。但这类模型共同的不足之处是：（1）该类方法普遍缺乏灵活性，对数据精度要求较高，当输入数据不全或存在偏差时，该类方法不能够进行灵活处理，导致预测出现较大误差；（2）考虑的影响因素相对较少，而且均为数量化影响因素。而那些对人口增长有较大影响的非数量化文本类知识因素，比如人口政策、经济发展、城市化进程等等，该类模型无法进行处理（见表1）。

2 创新型智能化人口预测方法

2.1 人工神经网络模型

1943年，心理学家麦卡洛克和数理逻辑学家皮茨首次提出了人工神经网络的概念，这对于统计预测领域产生了革命性的影响。人工神经网络是一种模拟大脑神经突触联接的结构进行信息处理的数学模型，这种模型具有自学习、联想存储、能同时处理定量和定性知识以及高速寻找优化解的能力，突破了传统统计类模型的机械式的预测方式的限制，使预测模型向着智能化的方向发展[10]。在此基础上，由Rumelhart和McCelland为首的科学家小组在1986年又提出了BP神经网络的概念，即一种按反向传播算法的多层前馈网络，成为目前应用最广泛的神经网络模型之一[11]。

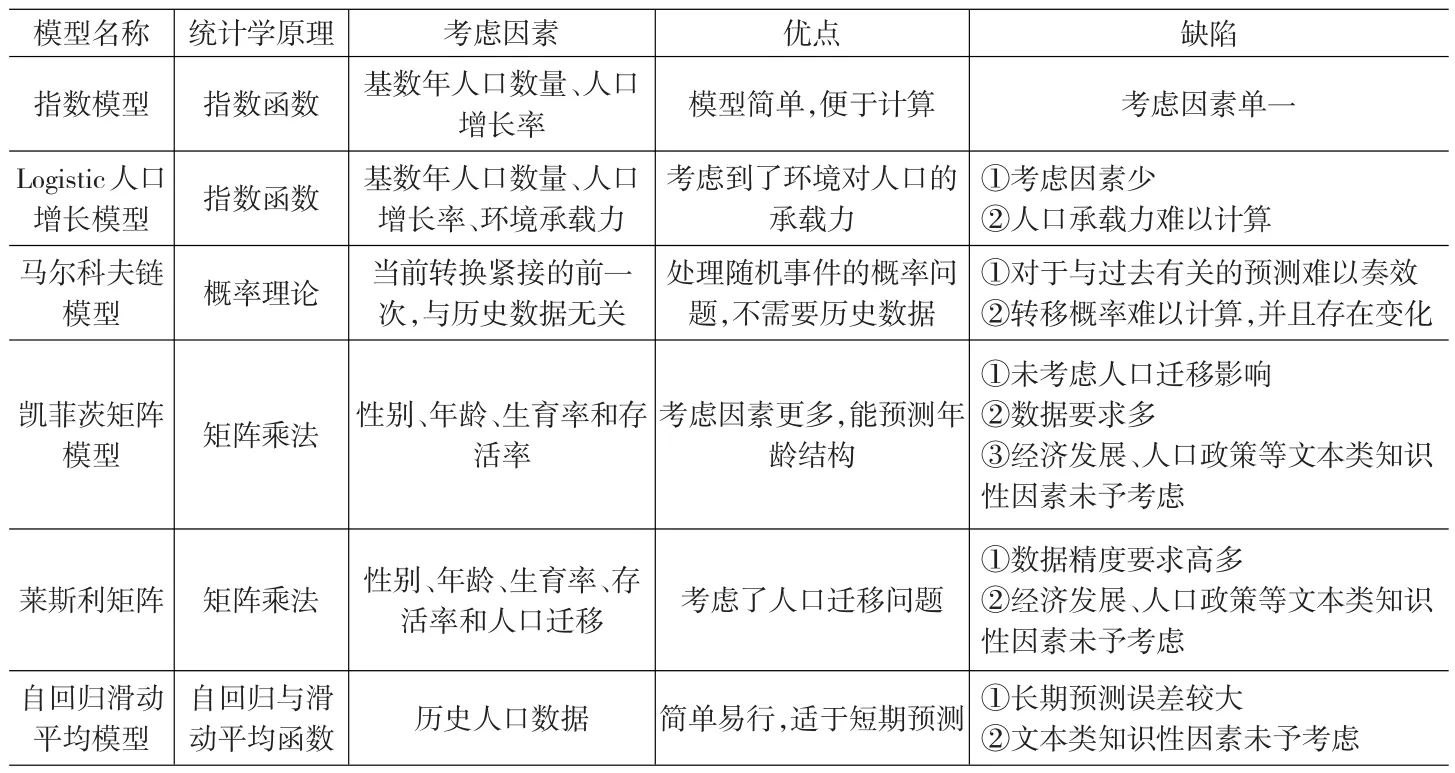
表1 西方传统的基于统计学原理的预测模型对比分析

随后，这种智能化的预测方法吸引了研究人口预测的学者们的注意，并将其引入这一领域。与传统的基于统计学原理的人口预测模型相比，这种新的模型具有以下优势：（1）可自学习和自适应不精准和不确定的系统，对于那些人口统计资料不系统和不完全精确的国家和地区来说，其应用的价值尤其大；（2）可以充分逼近任意复杂的非线性关系，而人口的增长与变化往往也是非线性的，无确定规律可循；（3）算法推导清晰，学习精度高，运算速度快；（4）所有定量或定性的信息都等势分布贮存于网络内的各神经元，故有很强的鲁棒性和容错性；（5）能够同时处理数字数据（如历史人口数据和生育率等）和文本数据（如经济、政策等因素对人口的影响）。

尽管神经网络模型有以上优点，但由于其在人口预测领域应用时间较短，依然存在着很多问题，如学习收敛速度缓慢、容易陷入局部最优、完全不能训练、网络的结构参数和学习参数的选取尚无统一指导等，这些缺点会导致预测的不稳定性和不精确性。因此，学者们又提出了各种算法对神经网络进行优化，以弥补其不足。

2.2 神经网络的优化方法

目前比较常用的对神经网络进行优化的算法主要有两种：遗传算法和群智算法。

2.2.1 遗传算法

在1975年，美国密歇根州大学约翰·霍兰德（J.Holland）教授通过借鉴生物界的进化规律，在模拟达尔文生物进化论的自然选择过程和遗传学机理的生物进化过程的基础上，提出了著名的遗传算法概念[12]。这种算法并不要求对象函数可求导或者连续，并且具有良好的全局寻优能力和概率化自适应能力。正是凭借这些优势，遗传算法常被用来作为神经网络的学习算法，或者来决定神经网络的拓扑结构。遗传算法与神经网络模型的这种结合，弥补了神经网络模型本身具有的学习收敛速度慢、易陷入局部最优的缺陷，使其在计算机科学和人工智能领域中得到了迅速的发展，在优化和预测方面有着重要的应用。

2.2.2 群智算法

随后，在上世纪90年代，又出现了一种新的应用广泛的算法——群智算法。其基本思想就是模拟自然界生物群体行为来构造优化算法[13]。其中，比较典型的算法有粒子群算法、人工鱼群算法和蚁群算法等。这些算法常常与神经网络模型结合起来使用。例如，粒子群算法的全局搜索能力可以用来优化神经网络的拓扑结构、连接权值和学习规则，或者是将神经网络嵌入到粒子群算法当中，利用神经网络良好的学习性能来改进粒子群算法的优化性能；而人工鱼群算法则凭借其对目标函数要求不高、算法对其内部参数设定容许范围较大、寻优速度较快和全局寻优能力较强等优点而作为神经网络模型的优化算法，得到广泛应用。

2.3 灰色模型

灰色理论是由中国著名学者邓聚龙教授在1982年首先提出来的，并以此为基础，建立了灰色模型GM(1,1)[14]。这种模型可以通过较少的、不完全的信息来对事物的长期发展规律做出模糊性的描述。其基本思想是，利用原始数据数列经累加生成新的序列，从而弱化原始数据的随机性，使其呈现出一定的规律，以此建立微分方程型的模型即GM模型，方便计算。灰色模型凭借这种只需考虑自身的时间序列，从中找到有用信息，发现和认识内事物内在的规律，从而进行预测，巧妙的躲过了繁杂的数据和影响因素，大大简化了计算量的优点，在人口预测领域得到了迅速的发展和广泛的应用。

但是在实际人口预测过程中，与其他预测方法相比，灰色模型也存在着一定的局限性：（1）当人口数据的离散程度较大时，预测精度会降低；（2）在长期人口预测中会存在较大的误差。

总体来说，相对于传统的基于统计学原理的人口预测模型而言，创新型智能化的人口预测模型具有以下几点明显优势：（1）可以并行处理大量的数量化影响因素，而统计类预测模型处理的影响因素较为有限；（2）对数据的精准性要求低于统计类预测模型；（3）可以处理一些对人口增长有重要影响的文本类知识性影响因素。但是，神经网络等智能化预测模型在模型结构的稳定性方面不如统计类预测模型，在实际应用中，其操作的难度也比统计类预测模型难度大（参见表2）。尽管如此，智能化预测模型仍然以其鲜明的优势，成为预测方法领域未来发展的主要趋势。

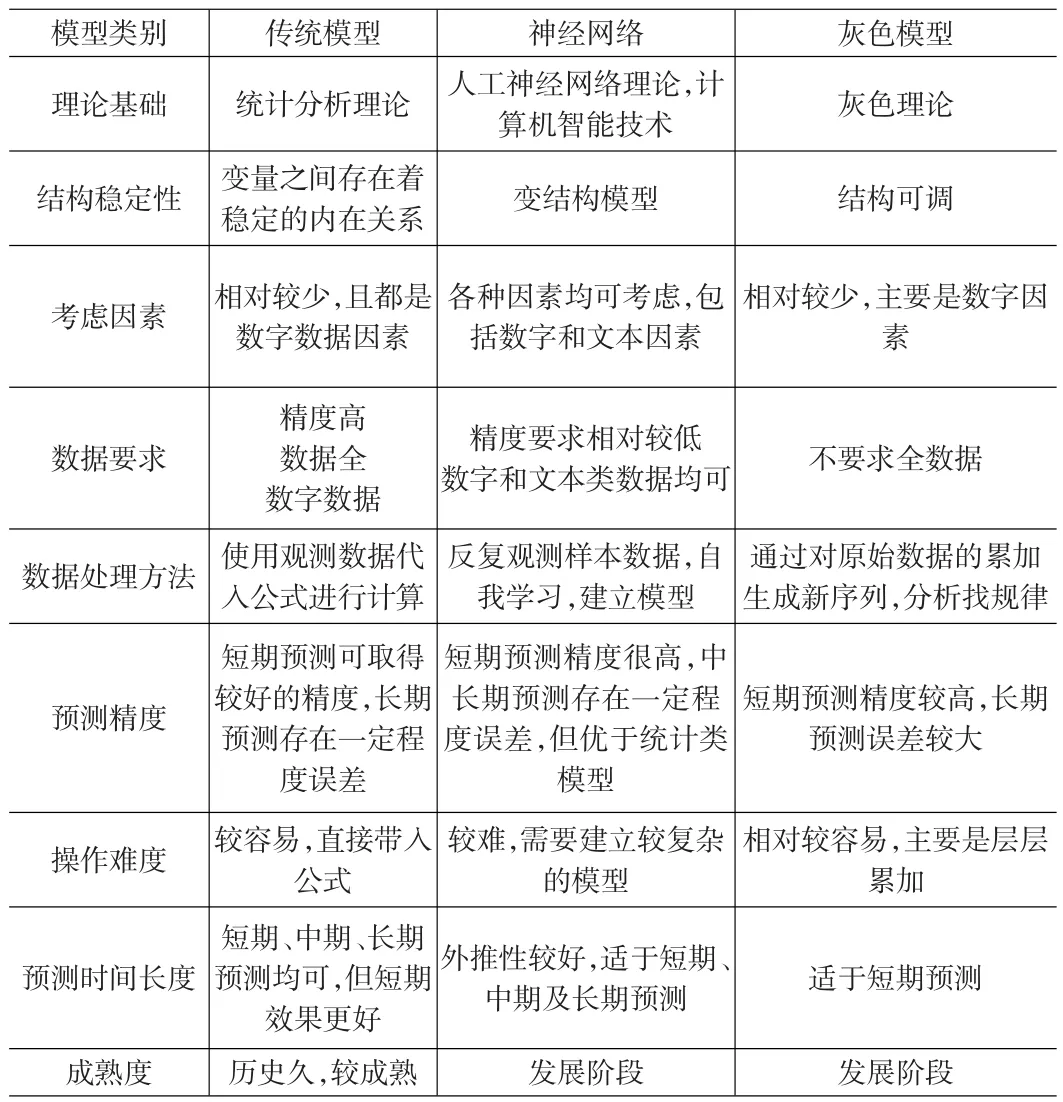
表2 两类预测模型对比分析

3 我国人口预测方法现状

3.1 我国学者自主构建人口预测模型

在自主构建预测模型方面，我国学者做出了很多努力。其中得到广泛认可和具有较大影响力的是著名控制论家宋健[15]等人于20世纪70年代末提出的人口发展方程。

其基本公式为[16]：

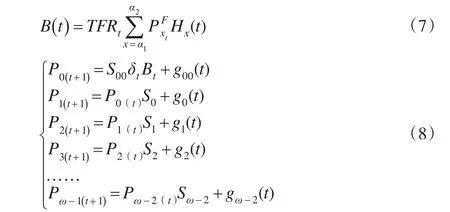
由以上公式可以看出，人口发展方程综合考虑了影响人口数量的多种因素，如生育率、年龄结构、生育胎次、迁移人数等等，相较于以前传统的预测模型而言，考虑的因素更加全面，易于推广。但作为一种基于统计原理的公式化的预测模型，其对于数据精度的要求很高，同时在模型中考虑因素较多，需要的数据也更多，其中很多数据有需要通过其他模型进行计算，这样就会导致某一数据细微的偏差，会对结果产生较大的影响。而且，对于净迁移人口数公式中没能给出具体算法，在实际中也是很难预测的。

3.2 应用西方统计类预测方法对我国人口进行预测

由于影响我国人口增长的因素较多，因此一些能够并行考虑多个影响因素的预测模型，比如Logistc模型、凯菲茨和莱斯利矩阵模型，在我国的人口预测中应用的比较多。且在应用过程中，我国的学者们还结合了我国的具体国情，对这些模型进行了适当的优化和改进。

在Logistic人口增长模型应用方面，考虑到环境对人口的承载力是很难计算的，并且在人口发生负增长的情况下是无法进行预测的，因而潘大志等人（2009）在原模型的基础上，考虑到环境资源的限制，添加了竞争项，建立了Logistic生物微分模型。这一模型相对于原始的Logistic人口增长模型具有更强的稳定性，对于模型中资源承载力的考虑也更加合理。文章最后还以四川省为例，对其人口进行了中长期预测，取得了良好的效果，平均误差控制在0.14%以内[17]。在对传统的Logistic人口增长模型进行推导求解的过程中，代涛等人（2010）认为，在实际中，相对于连续的动力方程模型，离散的模型更具可行性。通过对原始的Logistic人口增长模型离散化，代涛等人建立了离散的Logistic人口增长模型，即虫口模型。并通过引入混沌优化算法、非线性最小二乘法和高斯-牛顿法等数学方法，求得相应参数。模型还以湖北省1949～2005年历年总人口数为样本数据，采用了这一改进的Logistic人口增长模型对湖北省2010、2020、2030年的总人口进行了预测，得到了较好的短期预测效果[18]。但是这种模型所具有的最大的缺陷就是，对于公式中所需要的环境对人口承载力的数字表示依然难以准确把握，影响人口数量的文本类因素同样未能考虑进去，难以保证预测结果的精确性和稳定性。

在矩阵类人口预测模型的应用方面，王晓皋（1984）将凯菲茨矩阵模型引入国内人口预测领域，通过例证对凯菲茨矩阵模型的原理和计算过程进行了详细阐释，并分析了模型中的生育率、存活率等各参数的求解方法，使我们对于如何用矩阵乘法预测人口的原理一目了然[19]。朱艳伟（2010）则利用凯菲兹矩阵模型，采用逐年递推的方法对我国的人口进行了预测[20]。在预测中，生育率和存活率使用实际统计数据，采用逐年、循环计算的方式来预测人口增长趋势。但是，这种矩阵乘法预测模型的缺陷在于，它所需要的数据比较多，诸如生育率、存活率等因素每年都会变化，在长期预测中难以把握；同时，这种模型对于迁移因素导致的人口变化没有考虑，而这一因素对于一个地区人口的增长有着非常重要的影响。

3.3 应用创新型智能化预测方法进行人口预测

灰色模型、神经网络等创新型智能化预测方法的出现，为人口预测方法增加了新的预测手段，开辟了人口预测方法的一个新领域。

在灰色模型的应用方面，郝永红（2002）构建了一个灰色动态模型预测人口变化。在该模型中，只预测一个值，采用逐个预测依次递补的方式，逐步降低灰度，达到提高预测精度的目的，并利用1950年以后的人口数据，对1995年以后的人口进行了预测，5年预测误差控制在0.5%以内[21]。门可佩等人（2007）则又将灰色模型具体发展为离散灰色增量模型和新初值灰色增量模型，在两种模型下，相互对照，提高准确度。模型利用历年人口数据，对2003～2005年我国总人口数进行检验性预测，取得了较高的精确度[22]。

在神经网络模型的应用方面，吴劲军（2004）将BP神经网络模型引入人口预测领域，从这一模型的原理出发，结合人口预测的特点，论证了这一模型在人口预测方面的可行性。随后，又从配置阶段、训练阶段和预测阶段三个方面建立了人口预测的BP神经网络模型。并以江西省1949～1999年间的人口数据为基础，以江西省2000-2001年的人口数据作为检验数据，利用神经网络模型进行实际预测，相对误差仅为1%和0.2%[11]。尹春华等人（2005）通过实例，详细阐述了利用BP神经网络模型进行人口预测的步骤，并以辽宁沈阳某区的婴儿出生数量为例，进行了实例预测，结果与实际情况基本吻合[23]。作为一种新兴的智能化的预测方法，BP神经网络模型被引入国内人口预测领域的时间并不长，其中许多细节和具体操作仍有待改进，尤其是对于其中参数的设置、变量的引进，以及这种方法与Matlab等软件工具的结合需要进一步研究。

综上所述，随着时代的进步和新的预测技术的不断出现，我国人口预测方法在实践中也不断得到完善和发展。预测方法的发展突出表现在以下两个方面：（1）在影响因素方面，人口预测模型从仅考虑单一影响因素逐渐发展为同时考虑多个影响因素，对影响人口增长的影响因素考虑得越来越全面，预测精度也随之提高。（2）在预测模型的构建和应用方面，从仅应用和改进统计类预测模型逐步发展到应用和优化创新型智能化预测模型，将先进的人工智能技术逐步引入到人口预测领域中来，形成人口预测领域的新的发展方向，进一步提高了人口预测的有效性和准确度。

4 问题与改进对策

4.1 我国人口预测方法中存在的问题

（1）预测输入数据缺乏系统性，统计口径不统一的问题

目前我国人口预测中，每个预测者输入预测模型的数据都各不相同，即便是相同的影响因素，由于各地区统计口径的不同也存在差异。例如，对一个地区人口数量有重大影响的流动人口和迁移人口的统计，由于界定标准、统计方式的不同，不同部门、不同时间下就会有不同的结果[24]，这就会对整个地区人口数量的统计结果有很大影响，从而导致了预测结果的不准确性。由于没有形成符合我国国情的、囊括影响我国人口增长的全部数据类影响因素的完整的数据体系，因此，预测者们的预测结果无法加以比较。这种由于数据方面的不完整、不系统及统计口径的不统一，而导致的预测结果的不理想，成为我国人口预测过程中面临的首要问题。

（2）文本类知识性影响因素的挖掘与输入问题

目前人口预测所考虑的因素主要是数量化影响因素，但事实上，人口政策、经济发展、城市化进程、地理环境、甚至心理因素等一些非数量化的文本类知识因素对人口增长同样起到至关重要的作用。尤其是对北京、上海等大城市的人口增长进行预测时，如果不考虑生育政策、经济发展、城市化进程等一些对人口增长有重要影响的文本类知识性因素，只单纯的应用生育率、死亡率等数量化影响因素进行预测，那么无论使用何种先进的预测模型，其最终的预测结果都不会理想。因此，如何展开对人口增长有重要影响作用的文本类知识性影响因素进行深入的挖掘，如何对这一类的影响因素进行恰当的预处理，使之能够被带入预测模型，较大幅度提高预测精度，是我国乃至世界人口预测领域面临的前沿和难点问题之一。

（3）预测模型需要进一步完善的问题

目前我国人口预测中应用较多的预测模型依然是传统的基于统计学原理的预测模型，而统计类预测模型在我国的人口预测中主要存在以下方面的制约：（1）对数据的要求较高，如果数据不完整，有缺失，口径不统一，预测结果就不会理想；（2）尽管矩阵模型可以同时考虑多个影响人口增长的数量化因素，但却很难并行处理大量的数量化影响因素；（3）无法处理文本类知识性影响因素。而创新型智能化的神经网络预测模型，在可以并行处理大量数量化影响因素的同时，还可以在一定程度上处理文本类知识性因素。因此，创新型智能化预测模型在预测领域有巨大的发展空间，目前我国已有一些学者开始使用这类模型对人口增长进行预测，但仅仅出于初级尝试阶段，如何将统计类预测模型与智能类预测模型有机结合、如何对神经网络预测模型进行有效优化、如何将文本类知识性影响因素经恰当的预处理后带入智能化预测模型，最终提高人口预测精度，就成为人口预测领域面临的另一个前沿和难点问题之一。

4.2 改进对策

针对我国人口预测中存在的上述问题，我们应该在未来的人口预测方法方面着重开展并促进以下几个方面的研究工作：

（1）对影响我国人口增长的数量化影响因素进行数据挖掘，尽快构建影响我国人口增长的数量化影响因素的数据库。

运用数据挖掘方法对影响我国人口增长的各种数量化影响因素进行深入挖掘，并进行系统的排序、分析和整理；同时，对各种数量化指标的统计口径进行统一化的要求和处理。在此基础上，构建影响我国人口增长的数量化影响因素的数据库，为我国进行准确的人口预测奠定系统性数据基础，避免由于数据不系统和口径不统一造成的预测误差，同时使得预测模型的预测精准度在输入同类数据的基础上具有较强的可比性。

（2）对影响我国人口增长的文本类知识性影响因素展开知识挖掘，尽快构建我国人口增长文本类知识性影响因素的文本类知识库。

运用知识挖掘方法对影响我国人口增长的各种文本类知识性影响因素进行深入挖掘，进行知识发现、知识排序、知识推理、知识转化等一系列工作，最终构建我国人口影响因素的文本类知识库。将文本类知识性影响因素在人口预测中加以考虑，可以避免在预测中由于仅输入数量化影响因素、忽略知识性因素导致的预测精度不高的问题，尤其是在我国城市化进程不断加快的背景下，这种对文本类知识性影响因素的挖掘及其在预测中加以应用，对提高我国大中型城市人口增长的预测精度具有重要的作用。

（3）对智能化预测模型进行深入研究，引导我国人口预测方法尽快步入智能化预测的新阶段。

随着计算机技术和各种智能算法的不断发展，预测方法逐步朝着智能化的方向发展，智能预测不可避免的成为预测领域未来的发展趋势。运用神经网络智能预测方法对预测目标进行预测，在对数据处理和文本知识处理方面，具有统计类预测方法无法比拟的优势。当然，神经网络预测方法目前也存在需要进一步优化，提高运算速度、提高寻优能力以及提高结构稳定性等问题。因此，进一步研究如何对神经网络预测模型进行优化的各种方法，进一步研究如何将文本类知识因素经恰当的预处理后带入神经网络预测模型，通过对数量化影响因素和文本类知识因素的复合知识挖掘和复合知识输入，突破性提高我国人口预测精度，具有十分重要的意义。

[1]马尔萨斯.人口论[M].北京：北京大学出版社，2008

[2]Logistic Function,http://en.wikipedia.org/wiki/Logistic_function,2013,11(19).

[3]Seneta E.Markov and The Birth of Chain Dependence[J].International Statiscical Review,1966,64(3).

[4]Steven O.Markov Chains With Stochastically Stationary Transition Probabilities[J].The Annals of Probability,1991,19(3).

[5]李永胜.人口预测中的模型选择与参数认定[J].财经科学，2004，（2）.

[6]Nathan K.Applied Mathematical Demography[M].Springer Verlag,2005.

[7]任强，侯大道.人口预测的随机方法——基于Leslie矩阵和ARMA模型[J].人口研究，2011，35（2）.

[8]赵丽棉，黄基庭.基于Leslie模型的中国人口发展预测与分析[J].数学的实践与认识，2010，40（23）.

[9]朱兴造，庞飞宇.自回归及logistic离散模型在中国人口预测中的应用[J].统计与决策，2009，（13）.

[10]Javad G,NARGES Tayarani.Application of Artificial Neural Networks to The Prediction of Tunnel Boring Machine Penetration Rate[J].Science Direct(Mining Science and Technology),2010,20(5).

[11]吴劲军.人口预测的BP神经网络模型[J].理论新探，2004，（3）.

[12]EibenA E,Raué P E.Zs.Ruttkay.Genetic Algorithms With Multi-parent Recombination[J].Lecture Notes in Computer Science,1994,866.

[13]沈巍.股指波动预测模型的方法研究及应用[M].北京：知识产权出版社，2011.

[14]邓聚龙.灰色系统基本方法[M].武汉：华中科技大学出版社，2005.[15]宋健.人口预测和人口控制[M].北京：科学出版社，1982.

[16]蒋远营，王想.人口发展方程模型在我国人口预测中的应用[J].统计与决策，2011，（15）.

[17]潘大志，刘志斌.Logistic生物微分模型在人口预测中的应用[J].统计与决策，2009，(20).

[18]代涛，徐学军，黄显峰.离散Logistic人口增长预测模型研究[J].三峡大学学报(自然科学版)，2010，32（5）.

[19]王晓皋.用矩阵乘法预测人口[J].人口研究，1984，（6）.

[20]朱艳伟，张永利.中国人口增长预测模型及其改进[J].统计与决策，2010，（16）.

[21]郝永红，王学萌.灰色动态模型及其在人口预测中的应用[J].数学的实践与认识，2002，32（5）.

[22]门可佩，官琳琳，尹逊震.基于两种新型灰色模型的中国人口预测[J].经济地理，2007，27（6）.

[23]尹春华，陈雷.基于BP神经网络人口预测模型的研究与应用[J].人口学刊，2005，（2）.

[24]韦艳，张力.“数字乱象”或“行政分工”：对中国流动人口多元统计口径的认识[J].人口研究，2013,37（4）.