模糊综合评价中权重与评价原则的重新确定
王化中,强凤娇,陈晓暾
(陕西科技大学 管理学院,西安 710021)
模糊综合评价法作为一种以模糊数学为基础,利用模糊集理论进行评价的方法,已在管理科学、经济分析、环境评价等众多领域得到广泛应用[1,2]。但模糊综合评价方法理论本身研究较少,仍有需要改进的地方,本文将针对模糊综合评价方法的权重确定及归类原则两个方面的问题进行分析并针对存在的问题进行改进,力求使模糊综合评价方法在实际应用中更趋科学合理。
1 模糊综合评价方法中指标权重的重新确定
1.1 当前模糊综合评价方法中指标权重确定现状及存在的不足
模糊综合评价是应用隶属度向量将一些边界不清、不易定量的指标(因素)定量化,并考虑多种指标的影响下做出综合评价。该方法简单易行,不仅可评定对象所属的等级还可对不同评价对象排序。
目前模糊综合评价法中指标权重的确定有指标重要性赋权与指标分类(区分)性赋权两种。指标重要性赋权指计算的指标权重用以度量不同指标在综合评价过程中的相对重要性大小,可称为重要性权重,重要性权重与系统中评价对象各指标的取值或隶属度向量无关,它是指标自身关于评价目标与评价要求所具有的一种属性,不随具体评价对象或不同指标的取值变化而变化,属于固定权重,多采用层次分析法、德尔菲法等确定。指标分类性赋权指确定的指标权重用以度量不同评价指标取值或隶属度向量差异对区分评价对象属于不同类别所作贡献的大小,可称为分类性权重,分类性权重是针对特定一组对象及其各指标的具体取值而言的,一组评价对象中对象变化或对象的各指标取值变化,则指标的分类性权重变化,属于非固定权重,确定方法主要有信息熵、离差最大化法等。在具体的评价问题中,采用重要性赋权或分类性赋权来确定指标权重,其实是站在评价问题的不同侧面(角度)在看待问题,缺乏对评价对象多角度全面性的认识,关注的只是评价对象的一部分信息而非全面信息,从而使评价结果具有“片面性”[3]。
在实际评价中,指标权重的确定既要反映指标本身在评价中的重要性影响大小,又要通过不同指标具体取值尽可能的将不同评价对象区分开来,而重要性权重或分类性权重的思想都仅从一个侧面来分析确定各指标权重,只有将两类权重有机组合才可以从不同的侧面来获取评价对象的更多信息,从而使评价结果客观合理。
1.2 模糊综合评价方法中组合权重确定的思路及具体步骤
(1)模糊综合评价方法中组合权重的思想
以往文献中组合权重的思想,均是将主观方法确定的权重与客观方法确定的权重进行组合[3,4],本文提出将指标的重要性权重与分类性权重进行线性组合来确定模糊综合评价法权重的思想,如果评价工作更多的重视某一特定评价对象的客观性归类,对指标的重要性权重可给予较多的重视(即给予较大的系数),反之如果评价工作更多的重视通过不同评价指标将所有待评价对象区分开来,则对指标的分类性权重可给予较多的重视,组合权重的确定公式见式(1)。

本文将反映专家主客观意见的指标重要性权重用层次分析法确定,将不同对象各指标评价值(观测值)本身携带的客观分类信息所反映的分类性权重用离差最大化法计算得到,并将两者进行组合作为模糊综合评价的组合权重。
(2)层次分析法确定指标的重要性权重
层次分析法作为一种常用的决策方法与指标权重确定方法,能够将评价专家的主观与客观评价意见通过定性信息定量化的处理途径,转化为定量分析与计算,从而使复杂问题清晰化、简单化。
利用层次分析法确定指标的重要性权重,是通过将复杂问题分解为若干层次和若干要素(指标),通过两两比较的方式构造判断矩阵,计算判断矩阵就可得出不同指标的相对重要性权重。
(3)离差最大化法确定指标的分类权重
离差最大化法作为一种客观确定分类权重的方法,在多属性决策模型应用己经较为广泛[5-6]。该方法认为在对评价对象分类或排序时,应选择能够使评价对象的优劣区分开来的指标,故能够更大程度区分不同评价对象的指标其应赋予更大的权重[5~7],从而使得不同评价对象的差异能够最大程度的体现出来。
在模糊综合评价中确定指标的分类性权重,其基本思路是通过指标隶属度向量与其对应评语集的各标准值计算得到各指标期望分值,以期望分值为基础使得不同评价对象在所有指标上的加权总离差达到最大来建立模型,然后计算得到各指标的分类性权重。该思路的依据是对指标j而言,若所有评价对象的期望分值有较大差异,则指标j对于评价对象的分类与排序将起到较大作用,这样的指标应斌予较大的分类性权重;反之若期望分值差异越小,则说明j指标对所有评价对象分类与排序所起作用越小,这样的指标应斌予越小的分类性权重;当期望分值无差别时,则说明j指标对所有评价对象分类与排序不起作用,这样的指标其分类性权重应为0。

根据前面所述,分类性权重hj的确定应使所有指标对所有评价对象的期望分值加权总离差最大,为此构造最优化模型:

2 模糊综合评价方法中归类原则的重新确定
2.1 “最大隶属度”归类原则存在的问题
模糊综合评价结果给出的不是严格的等级(类别)归属,而是通过综合隶属度向量给出评价对象隶属于不同类别的度。当前模糊综合评价中普遍采用“最大隶属度”归类原则,“最大隶属度”归类原则是一种简单但粗糙的归类原则,该原则最大程度的突出了占优势类别的作用,具有一定的合理性,但因其仅仅依据隶属度向量中的最大隶属度来确定评价对象所属类别,对隶属度向量中的其余分量完全忽视,显然存在一定的片面性。在综合隶属度向量较为分散时,使用该原则就可能导致归类错误,从而出现不同评价对象所属归类与其排序不一致的问题,即在由优到劣排序中靠前的评价对象不一定归类更优,归类更优的对象由优到劣排序不一定靠前(如本文实例中的课题1与课题5)。
2.2 模糊综合评价方法归类原则的改进
为有效避免评价对象所属归类与其排序不一致的情况,重新设计模糊综合评价方法归类原则的思路是将综合隶属度向量当成一个完整的体系,综合隶属度向量中的任一分量均对评价对象的归类起作用,基于所有分量的共同作用效果来进行归类。本文基于系统化思想重新设计了模糊综合评价方法的归类原则,称其为“最短距离”归类原则。假设第1,2,…,s类别为从劣到优排列,“最短距离”归类原则基本步骤如下:
通过评语集的各标准值与评价对象i综合隶属度向量求得综合评价值Vi。
将综合评价值Vi与评语集的各标准值对比,如果Vi≤p1,则评价对象i属于第1类;如果Vi≥ps,则评价对象i属于第s类;如果Vi介于两个最接近的相邻评语标准值pk(k=1,2,…,s-1)和pk+1之间,即pk≤Vi≤pk+1,分别计算Vi与pk和pk+1之差的绝对值,将评价对象i归类到其中与其评语的标准值之差绝对值较小的类别中,即利用公式对评价对象i进行归类。
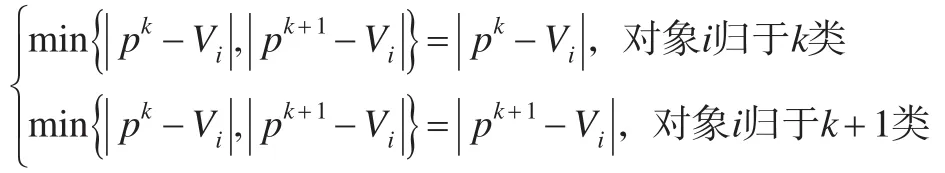
3 实例分析
某高校为合理选择科研课题,由15位评价专家对5个申报课题采用模糊综合评价方法进行评选,其评选采用的指标体系如图1所示[1]。
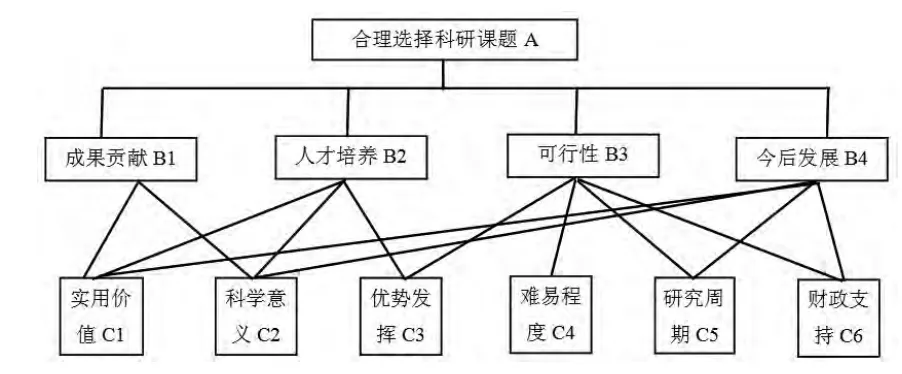
图1 科研课题评选指标体系
其中,经统计后科研课题1的评价表见表1所示。
3.1 确定评价各分指标隶属度向量,并形成隶属度矩阵R
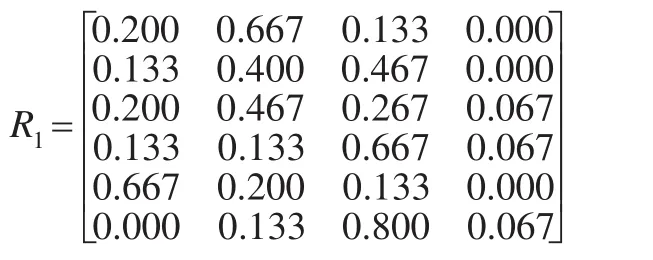
对表1中的数字均除以专家总人数15并转置,可得到课题1各指标对评语集的隶属度矩阵R1为
3.2 确定组合权重向量w
利用层次分析法确定指标的重要性权重
课题组专家在充分讨论的基础上,分别建立A-B,B1-C,B2-C,B3-C,B4-C的判断矩阵,其中A-B的判断矩阵及利用方根法对判断矩阵的计算与检验结果见表2所示。
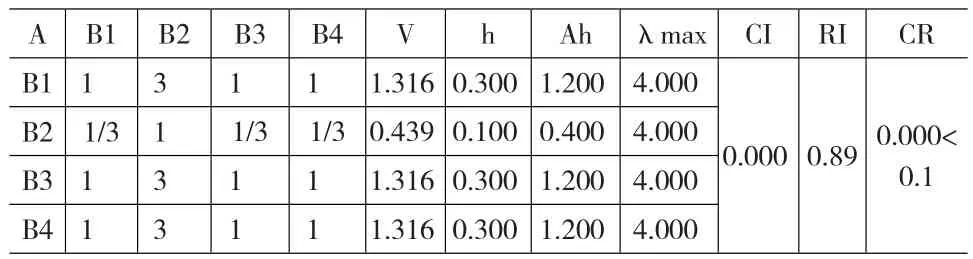
表2 A-B的判断矩阵及其对判断矩阵的计算与检验结果
同理,对B1-C,B2-C,B3-C,B4-C等判断矩阵进行计算并检验(略),然后建立C层元素对A层的总排序,结果见表3所示。

(2)利用离差最大化法确定指标的分类性权重
该校确定评语集的评语好、较好、一般、较差相对应的标准值分别为100、80、60、40,则课题1的C1指标的期望分值为:
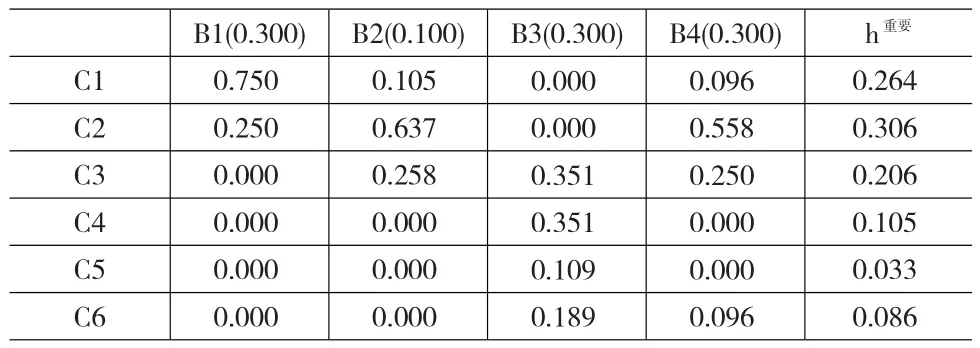
表3 C层对A层的总排序
e11=0.200×100+0.667×80+0.133×60+0.000×40=81.333
同理得:e12=73.333,e13=76.000,e14=66.667,e15=90.667,e16=61.333。
依照对课题1的计算,同样可得到其余4个课题各指标期望分值,5个待评价课题各指标的期望分值见表4所示。
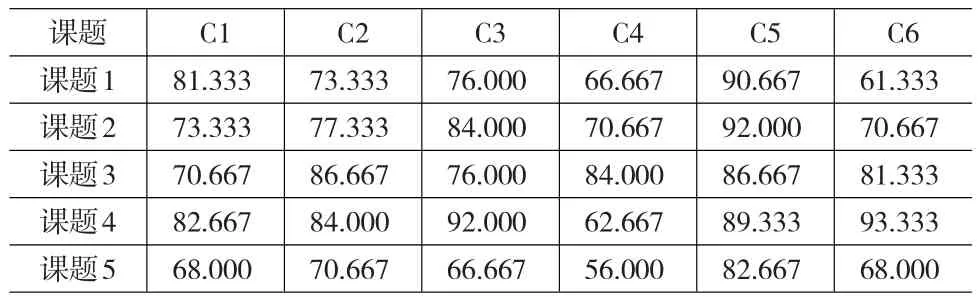
表4 5个科研课题各指标期望分值表

(3)确定科研课题评价指标的组合权重
在本次科研课题评选中,评价组相对较多的关注特定评价课题的客观性归类,并兼顾不同评价课题的区分性归类,故确定重要性权重系数α取值为0.6,利用式(1)可得6个科研课题C1-C6指标的组合权重W=(0.211,0.240,0.200,0.147,0.049,0.153)。
3.3 计算综合评价隶属度向量S及综合评价值V
将指标的组合权重W与隶属度矩阵R1,利用矩阵的普通乘法运算进行综合,则科研课题1的综合评价隶属度向量S1=WR1=(0.1664,0.3798,0.4205,0.0335);课题1的综合 评 价 值V1=0.1664×100+0.3798×80+0.4205×60+0.0335×40=73.594。同理可计算其余4个课题综合评价隶属度向量与综合评价值,5个待评选课题综合隶属度向量、最大隶属度与综合评价值见表5所示,依据综合评价值确定的评价课题从优到劣的顺序用①~⑤表示,结果见表5。

表5 5个科研课题综合隶属度向量、最大隶属度、综合评价值及排序表
如果采用最大隶属度原则,则课题4属于“好”类,课题2、3与5属于“较好”类,课题1属于“一般”类。将各课题归类与其排序对比发现,课题1的综合评价值73.594大于课题5的综合评价值67.316,即说明课题1优于课题5,但课题1归类却比课题5差。
为了更清楚,将表4中课题1与课题5各个指标的期望分值进行比较发现,总共6个指标中,课题1的C1-C5共5个指标均明显大于(优于)课题5的相应指标,只有在C6指标上课题1小于(劣于)课题5,所以得出课题1优于课题5的结论是显而易见的,这也从另一角度说明将课题1归类比课题5差的结论是错误的。本例进一步证明依据“最大隶属度”原则不能有效保证归类正确,也无法避免归类与排序的不一致现象。
依据本文设计的归类原则,对课题1来讲,课题1的综合评价值73.594介于两个最接近的评语“较好”的标准值80与评语“一般”的标准值60之间,计算课题1的综合评价值73.594与“较好”的标准值80差的绝对值为6.406,与“一般”的标准值60差的绝对值为13.594,显然课题1的综合评价值与“较好”类别的标准值80更接近,故得出课题1综合评价结果应属于“较好”类别。同理可得到其余课题归类,依据本文准则对5个课题的归类计算及归类结果见表6所示。
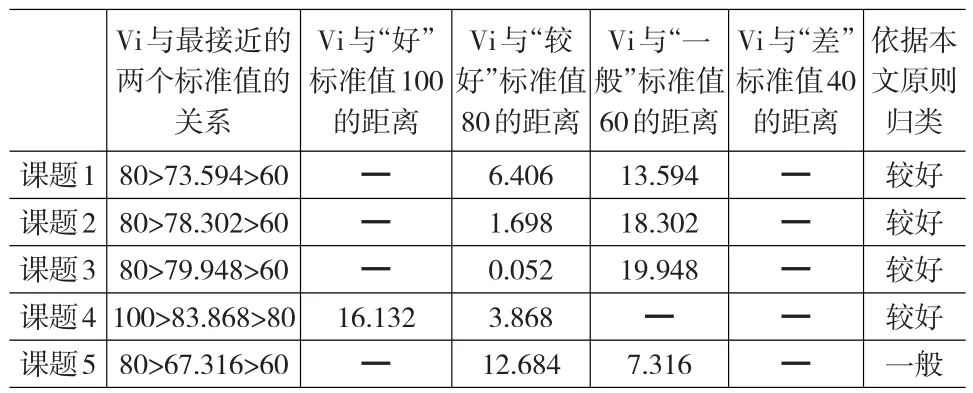
表6 依据本文准则对5个课题的归类计算及归类结果表
将本文确定的归类结果与采用“最大隶属度”原则归类结果对比发现,以本文原则课题1由原来的“一般”类变为现在的“较好”类,课题5则由原来的“较好”类变为现在的“一般”类,新归类与课题1和5的优劣排序结果一致;课题2与3归类没有变化;课题4由原来的“好”类变为现在的“较好”类,将表4中课题4各指标的期望分值与各评语集的标准值对比发现,有3个指标与“较好”类的标准值接近,有1个指标值与“一般”类的标准值接近,有2个指标值与“好”类的标准值接近,故课题4综合评价结论属于“较好”类别更为合理。从本例可以进一步说明采用本文设计的归类原则,考虑问题更加全面系统,5个课题的归类与表5中的课题排序对照没有出现不一致的情况。
对本次该校合理选择科研课题,根据学校实际情况对课题从优到劣排序来选择排序最靠前的几个课题,如果只选一个课题,自然首选课题4。如果该校课题申报较多,则可以在归类的基础上,对类内的对象排序并选择。
4 总结
针对模糊综合评价中权重确定存在的问题,本文提出将指标的重要性权重与分类性权重组合来确定模糊综合评价法权重的思想,重点介绍了利用离差最大化法思想在模糊综合评价中确定指标分类性权重的思路及过程,同时对模糊综合评价中普遍采用的“最大隶属度”归类原则存在的不足进行分析,设计了新的称为“最小距离”的归类原则。通过实例分析与应用,以详细的计算步骤及结果分析证明了本文设计思路及改进效果的可靠性。
[1]汪应洛.系统工程(第4版)[M].北京:机械工业出版社,2008.
[2]张志英.模糊评价法在本科毕业设计成绩评定中的应用[J].浙江理工大学学报,2011,(03).
[3]庞彦军,刘开第,吴海玉等.指标分类权重的概念及其应用[J].河北建筑科技学院学报,2005,(04).
[4]李珠瑞.离差最大化思想下的组合评价研究[D].合肥工业大学,2012.
[5]陈自力,李尊卫.离差最大化法在商业银行内部控制评价中的应用[J].重庆大学学报(自然科学版),2005,(10).
[6]霍叶青,何跃.基于离差最大化和Ward系统聚类的四川城镇化水平研究[J].软科学,2010,(06).
[7]张荣,刘思峰,刘斌.基于离差最大化客观赋权法的一般性算法[J].统计与决策,2007,(24).

