基于模拟退火算法的无人驾驶车辆轨迹跟踪控制

王 浩，林 棻，张尧文

(南京航空航天大学能源与动力学院车辆工程系，南京 210016)

基于模拟退火算法的无人驾驶车辆轨迹跟踪控制

王 浩，林 棻，张尧文

(南京航空航天大学能源与动力学院车辆工程系，南京 210016)

研究了基于模拟退火算法(SA)的无人驾驶车辆横向控制策略。建立了线性离散车辆运动学预测模型，考虑位姿偏差和控制量的变化设计目标函数，运用模拟退火算法(SA)对目标函数进行求解并获得当前时刻的控制增量，进而实现无人驾驶车辆的轨迹跟踪控制。通过在低速组合轨迹工况下的仿真结果表明:在不同的车速下，该控制策略能够保证车辆快速平稳地跟踪给定参考轨迹，位置误差能够控制在0.05 m之内，具有较好的控制效果。

无人驾驶车辆;模型预测控制;模拟退火算法;轨迹跟踪

随着科技的日益进步，无人驾驶车辆开始逐渐进入人们的视野［1］。目前，轨迹跟踪控制是无人驾驶车辆研究的基本问题，只有在具备跟踪预期路径的能力下才能更进一步地探讨无人驾驶车辆的其他性能。

目前，国内外许多科研机构对无人驾驶车辆的轨迹跟踪问题进行了研究。文献［2］采用滑模控制方法设计轨迹跟踪控制器，但产生的抖振现象对车辆和驾乘人员有不利影响。文献［3］采用模糊控制方法设计轨迹跟踪控制器，但稳定性判据较难建立，且不具备自学习能力。文献［4］采用神经网络PID方法设计轨迹跟踪控制器，具备自学习能力，但鲁棒性欠佳。

无人驾驶车辆系统具有非线性、时变性等特性。模拟退火算(simulated annealing，SA)是一种求解非线性问题的全局优化算法，对初值鲁棒性强，且应用简单。因此，本文将SA算法与模型预测控制相结合设计了无人驾驶车辆轨迹跟踪控制器。

1 车辆运动学模型

无人驾驶车辆的轨迹跟踪控制是通过对车辆系统的控制来实现的。在路面状况良好的低速行驶工况下，一般不需要考虑车辆稳定性控制等动力学问题［5］。因此，本文采用车辆的运动学模型作为预测模型［6］。

无人驾驶车辆运动学模型可以简化为两轮自行车模型。在平面直角坐标系下，车辆的运动学模型如图1所示。在惯性坐标系oxy下，(xr，yr)和(xf，yf)分别为车辆后轴和前轴轴心的坐标，vr和vf分别为车辆后轴和前轴中点的速度，φ为车辆的航向角，δf为前轮转角，l为车辆前后轴轴距。

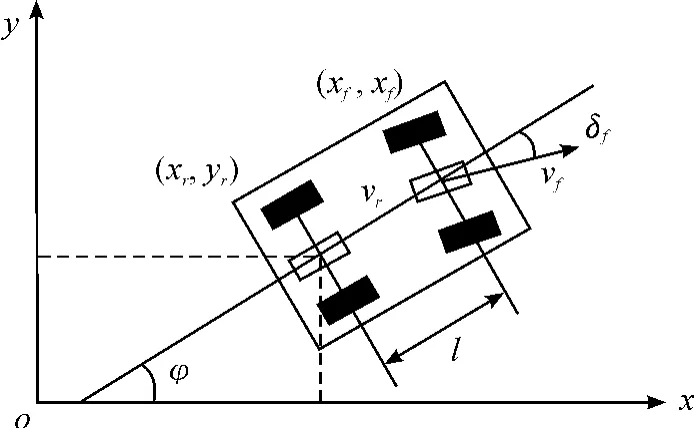
图1 车辆运动学模型

由图1中的运动学关系得:

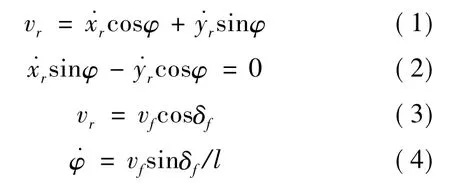
整理化简式(1)～(4)，得车辆的运动学模型:

式中:x˙r为车辆后轴中点处的横向速度;y˙r为车辆后轴中点处的纵向速度。

为了表示方便，下文中的x=［x，y，φ］T，u=［v，δ］T与上文中的x=［xr，yr，φ］T，u=［vr，δf］T意义相同。

式(5)的一般形式表示为

轨迹跟踪问题一般是通过控制实际车辆跟踪参考车辆来实现的。因此，假设参考车辆行驶通过给定的参考轨迹，则参考车辆各个时刻的状态量和控制量满足上述方程。用d表示参考量，其一般形式表示为［5］

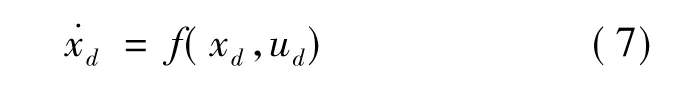
其中:xd=［xd，yd，φd］T;ud=［vd，δd］T。

在任意参考轨迹点处将式(6)以泰勒级数形式展开，并忽略高阶项:

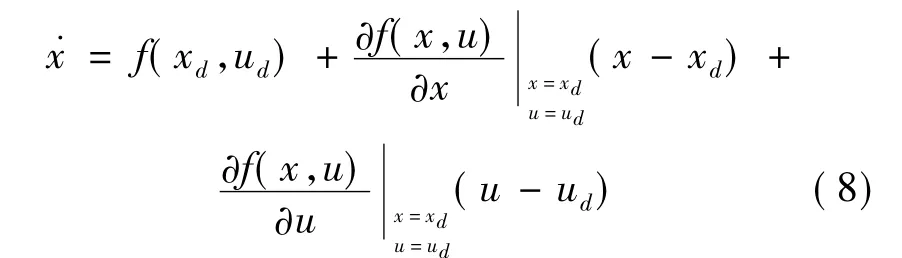
式(8)与式(7)相减得

式中:

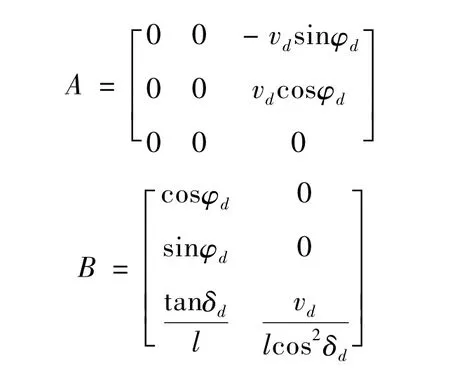
本文采用的线性模型预测控制(model predictive control，MPC)［7］是一种离散时间控制方法，因此需要对式(9)表达的车辆运动学模型的连续状态方程进行离散化处理:

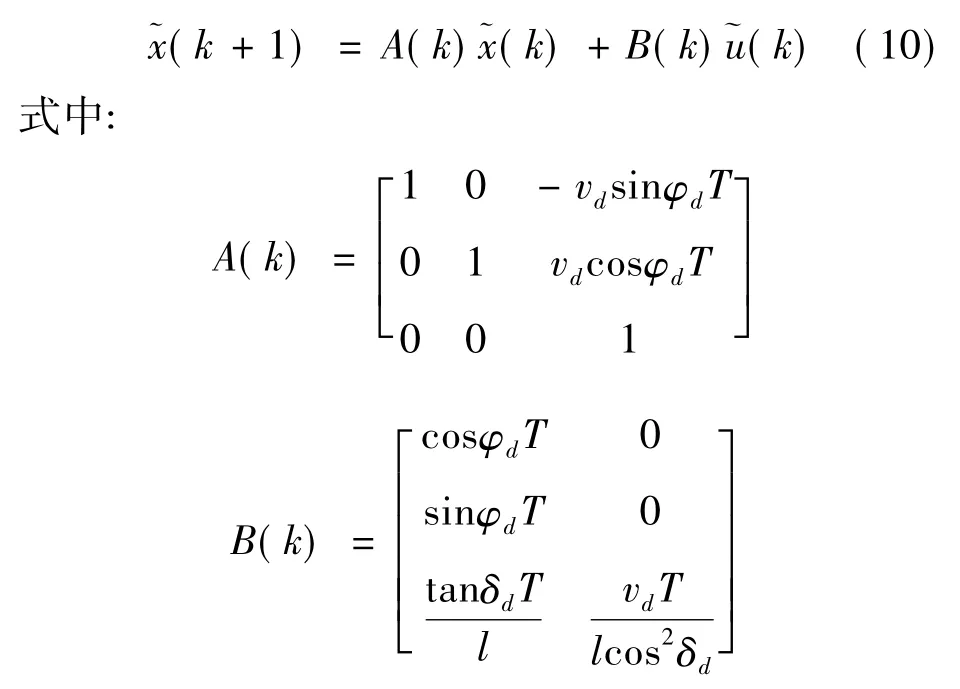
其中，T为采样时间。

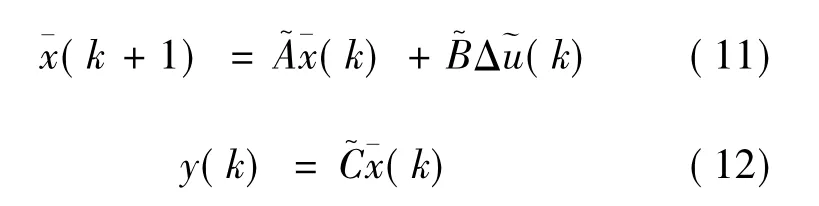
式(11)和(12)即为线性离散化的车辆运动学模型，将该模型作为MPC的预测模型。

2 基于MPC的轨迹跟踪控制算法

MPC通过建立的预测模型，预测系统在当前状态施加一定的控制作用后未来的状态或输出，并根据其约束条件和性能指标求解最优的控制序列，对控制对象施加当前控制量，通过实时检测来修正对未来状态或输出的预测。如此往复循环，以实现对控制对象的控制［7］。

MPC易于建模、控制效果好、鲁棒性强，可以处理多变量和有约束的问题，并且能够实现反复在线优化［8-9］。

2.1 预测方程

在式(11)和(12)的基础上推导预测方程，以实现对车辆系统未来各个时刻输出的预测。设预测时域为Np，控制时域为Nc。由式(11)和(12)可以预测出在Nc个控制增量的作用下未来Np个时刻车辆系统的输出，用矩阵形式描述为

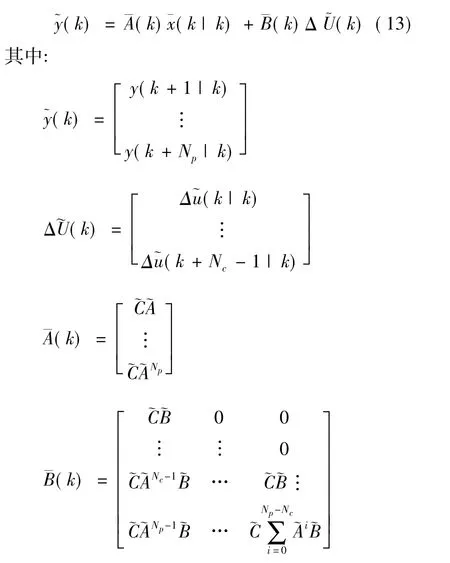
2．2 目标函数和约束条件设计

车辆系统当前的状态量是已知量，控制量是未知量，因此需要设计合理的目标函数，将车辆系统的控制量作为设计变量，通过求解目标函数得到控制时域内的控制量序列。

为了保证无人驾驶车辆能够快速且平稳地跟踪参考轨迹，需要对车辆预测位姿与参考位姿的偏差和控制量的变化进行优化。由于系统模型的时变特性，在目标函数中加入松弛因子，以确保每个时刻都可求得可行解［5］。因此，选取目标函数:

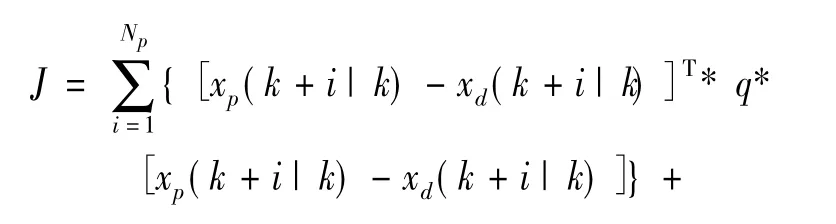
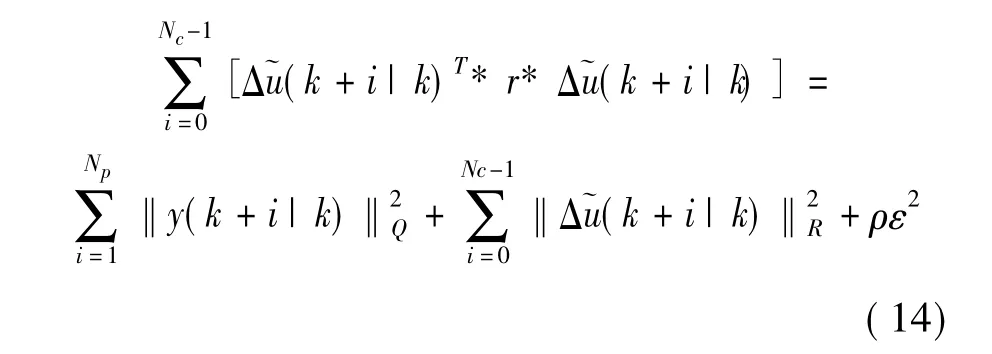
式中:第1项考虑了车辆预测位姿与参考位姿的偏差，表征了车辆系统跟踪参考轨迹的能力;第2项考虑了控制量的变化，以保证控制量变化平稳;Q和R为目标函数中适当维数的状态和控制加权矩阵，Q=diag(q q…q)，R=diag(r r…r);ρ为权重系数;ε为松弛因子;xp(k+i|k)为k时刻对未来第k+i时刻车辆系统的实际状态量的预测;xd(k+i|k)为未来k+i时刻车辆系统的参考状态量;y(k+i|k)的实际含义为未来第k+i时刻车辆系统的实际状态量的预测值与参考状态量的偏差;为第k+i时刻车辆系统的实际控制增量的预测值。

为了避免控制量的突变，保证控制量变化的连续性，使无人驾驶车辆轨迹跟踪过程更加平稳，对控制增量设置约束条件:

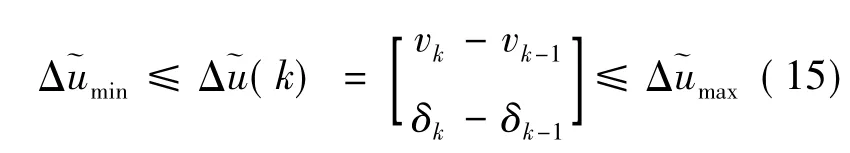
2．3 目标函数求解

将上述问题转化为求解以下带有上下界约束的多变量单目标优化问题:

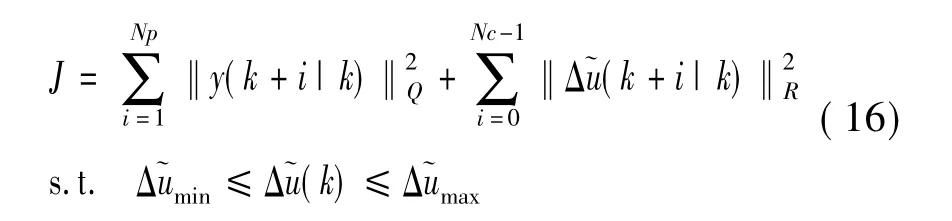
本文采用模拟退火算法(SA)对目标函数进行优化求解。SA算法可以求解不同的非线性问题，对初值有较强的鲁棒性，简单通用，并且易于实现，是一种全局优化算法［10］。对于该非线性优化问题，设计变量和目标函数已确定，运用SA算法进行优化求解，步骤如图2所示。

求解所得的设计变量最优解即为当前时刻车辆系统的控制增量序列:

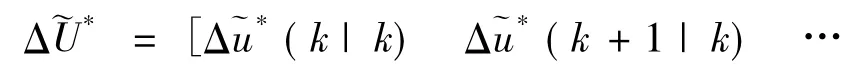
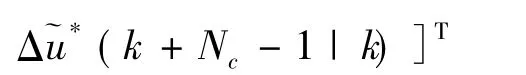
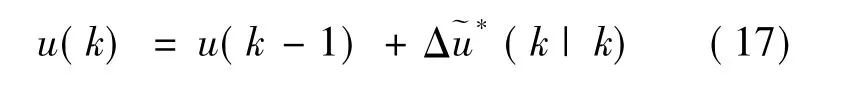
到下一时刻，预测时域和控制时域随着时间的推进向前滚动推移。如此循环往复，便可以实现无人驾驶车辆的轨迹跟踪控制。

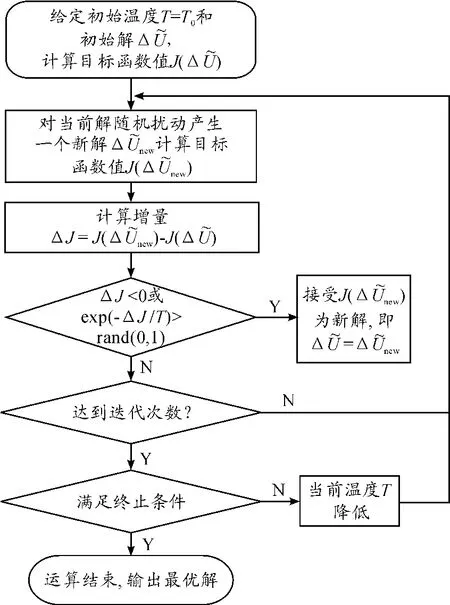
图2 SA算法流程

3 仿真验证

为了验证所设计的MPC轨迹跟踪控制器的性能，本文在Matlab环境下进行了仿真试验。

仿真试验所采用的参考轨迹为直线轨迹与圆形轨迹的组合轨迹。分别在车辆参考纵向速度为5，10 m/s的情况下进行仿真试验。直线轨迹跟踪阶段的参考前轮转角为0 rad，圆形轨迹跟踪阶段的参考前轮转角为0.129 5 rad。车辆的初始状态为［0 -5 0］，即初始横向位置为0 m，初始纵向位置为-5 m，初始航向角为0 rad。采样时间T=0.05 s，轴距l=2.6 m。所采用的MPC轨迹跟踪控制器的主要性能参数为:预测时域Np=60，控制时域Nc=40，Q=diag(q，q，…，q)Np×Np，q=diag(10 1 1)，R=500×INu×Nc，ρ=10，Δvmin= -0.05 m/s，Δvmax=0.05 m/s，Δδmin=-0.008 2 rad，Δδmax=0.008 2 rad。所采用的模拟退火算法的参数如下:最大迭代次数为500，初始温度为100℃，采用指数降温。

仿真试验结果如图3～7所示。图3为不同参考速度下的车辆实际轨迹与参考轨迹;图4～5分别为不同参考速度下的位姿偏差。由图3～5可知:在车辆初始位置与参考轨迹存在初始偏差、参考速度不同的情况下，车辆在MPC轨迹跟踪控制器的作用下均能快速地跟踪上参考轨迹，随后其位置偏差控制在0.05 m内，航向角偏差也在较短时间内收敛为0;在参考速度较低的工况下，车辆的实际轨迹与参考轨迹更为接近，且跟踪上参考轨迹后的位姿偏差更小，但在参考速度较高的工况下车辆依然有良好的跟踪效果，参考速度的提高并没有导致跟踪性能的下降。因此，本文所设计的MPC轨迹跟踪控制器能够实现车辆对参考轨迹的快速跟踪，并且对车辆纵向速度的变化具有较强的鲁棒性。

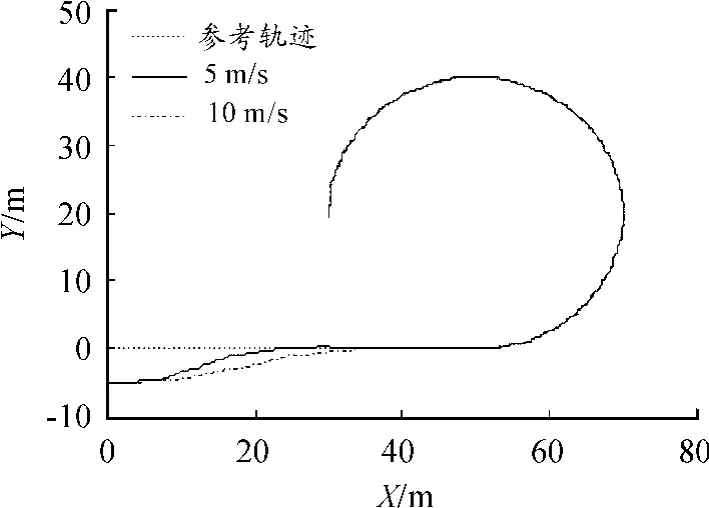
图3 不同参考速度下的车辆实际轨迹与参考轨迹

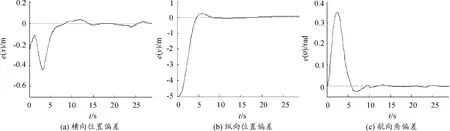
图4 参考速度为5 m/s时的位姿偏差

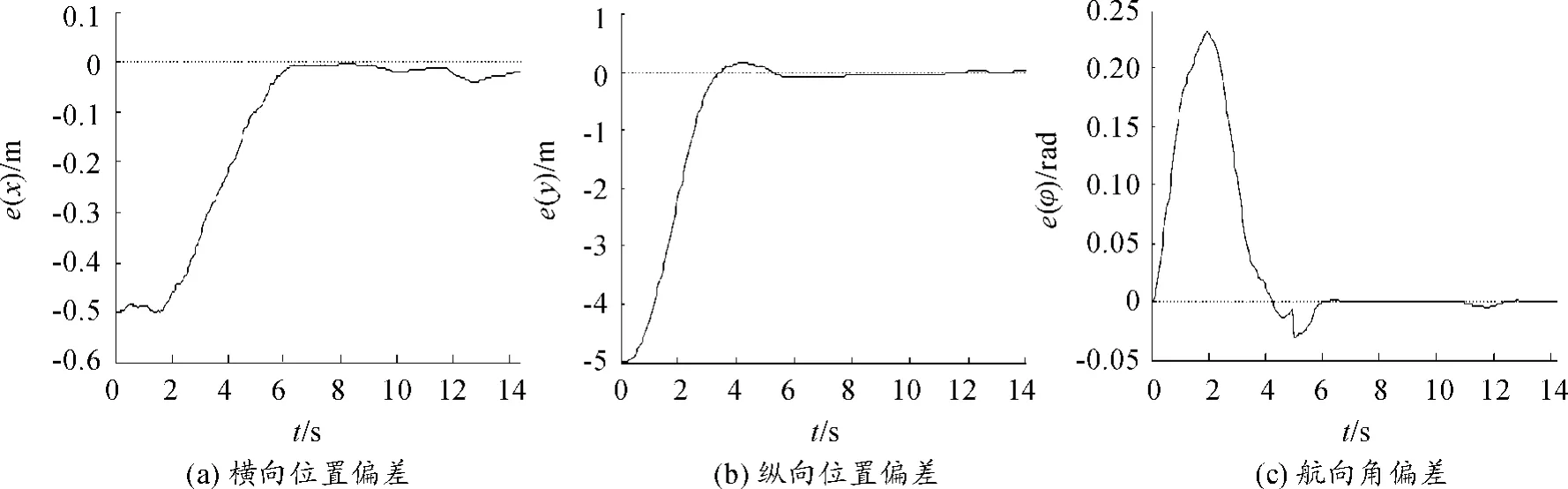
图5 参考速度为10 m/s时的位姿偏差

图6～7分别为不同参考速度下的控制量变化。由图6～7可知:由于存在初始偏差，在初始的一段时间内，车辆的纵向速度和前轮转角不断调整，以保证车辆能够较快地跟踪参考轨迹。随后车辆的纵向速度和前轮转角逐渐跟踪上参考值，并几乎保持不变。由于圆形轨迹与直线轨迹

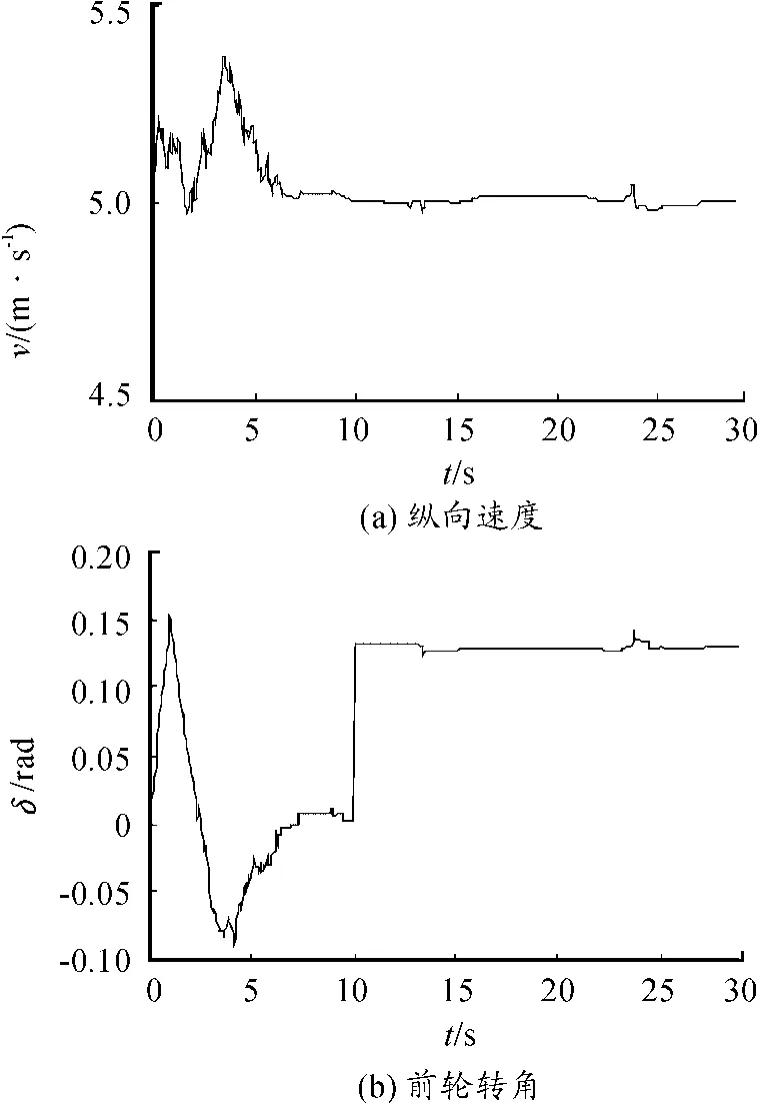
图6 参考速度为5 m/s时的控制量变化

4 结束语

将SA算法与MPC进行结合解决无人驾驶车辆的轨迹跟踪问题。建立了车辆运动学模型，设计了MPC轨迹跟踪控制器，并运用SA算法对控制量进行优化，对车辆的纵向速度和前轮转角进行控制。

本文设计的控制器能实现无人驾驶车辆对参考轨迹的快速跟踪，并且能保证轨迹跟踪的平稳性和鲁棒性。轨迹跟踪的位置误差能够控制在0.05 m之内。

在参考速度较低的工况下，车辆的实际轨迹与参考轨迹更为接近，且跟踪上参考轨迹后的位的参考前轮转角有所不同，因此，车辆从直线轨迹向圆形轨迹过渡时，其前轮转角会有所变化。随着参考速度的提高，控制量的变化加大，但均在约束范围内，变化比较平稳，因此本文所设计的控制器能够实现车辆对参考轨迹的平稳跟踪。姿偏差更小，控制量的变化也更小。在参考速度较高的工况下车辆依然有良好的跟踪效果，控制量的变化也均在约束范围内，参考速度的提高并没有导致跟踪性能的下降。

图7 参考速度为10 m/s时的控制量变化

［1］Ozguner U，Acarman T，Redmill K.Auto-nomous Ground Vehicles［M］.Boston:Artech House，2011.

［2］Hamerlain F.Trajectory tracking control of a car-like mobile robot in presence of sliding［C］//2012 UKACC International Conference on Control.Cardiff:IEEE，2012: 502-507.

［3］Mahapatra S，Patle B K，Jha A K，et al.Fuzzy logic control of a WMR［C］//2012 International Conference on Computing，Communication and Applications.Dindigul: IEEE，2012:1-5.

［4］Singh A，Bisht G，Padhy P K.Neural network based adaptive nonlinear PID controller for non-holonomic mobile robot［C］//2013 IEEE International Conference on Control，Automation，Robotics and Embedded Systems.Jabalpur:IEEE，2013:1-6.

［5］徐威，龚建伟，姜岩.无人驾驶车辆模型预测控制［M］.北京:北京理工大学出版社，2014.

［6］刘子龙，杨汝清，杨明，等.无人驾驶车辆横向位置最优跟踪控制［J］.上海交通大学学报，2008(2):257 -261.

［7］席裕庚.预测控制［M］.2版.北京:国防工业出版社，2013.

［8］胡国龙，孙优贤.预测控制进展及其应用研究［J］.电力系统及其自动化学报，2003(1):109-114.

［9］Mousavi M A，Heshmati Z，Moshiri B.LTV-MPC based path planning of an autonomous vehicle via convex optimization［C］//2013 21st Iranian Conference on Electrical Engineering.Mashhad:IEEE，2013:1-7.

［10］Afifi S，Dang D C，Moukrim A.A Simulated Annealing Algorithm for the Vehicle Routing Problem with Time Windows and Synchronization Constraints［J］.Lecture Notes in Computer Science，2013:259-265.

(责任编辑杨黎丽)

Research on Trajectory Tracking Control of Self-Driving Vehicle Based on Simulated Annealing Algorithm

WANG Hao，LIN Fen，ZHANG Yao-wen
(Department of Automotive Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China)

Lateral control based on simulated annealing(SA)algorithm was investigated for trajectory tracking of self-driving vehicle.Firstly，the linear discrete kinematics model was established.Based on this model，considering position and pose error，the objective function and constraint condition were designed，and simulated annealing(SA)algorithm was used for optimization problems and obtaining the optimal control variables and the trajectory tracking control was achieved.In the condition of low speed and combined trajectory，the simulation results show that in different speeds，the control strategy guarantees that the vehicle can follow the reference trajectory stably and rapidly with good effect，and the position error can be kept within 0.05 m.

self-driving vehicle;model predictive control;simulated annealing;trajectory tracking

TP273

A

1674-8425(2015)11-0106-06

10.3969/j.issn.1674-8425(z).2015.11.018

2015-06-28

国家自然科学基金资助项目(10902049);江苏省博士后科研资助计划项目(1302020C);中央高校基本科研业务费专项资金资助项目(NS2015015);南京航空航天大学研究生创新基地(实验室)开放基金资助项目(kfjj201404)

王浩(1989—)，男，硕士研究生，主要从事车辆系统动力学研究;通讯作者 林棻(1980—)，男，博士，副教授，主要从事车辆动力学与控制、汽车现代设计方法等方面研究。

王浩，林棻，张尧文.基于模拟退火算法的无人驾驶车辆轨迹跟踪控制［J］.重庆理工大学学报:自然科学版，2015(11):106-111.

format:WANG Hao，LIN Fen，ZHANG Yao-wen.Research on Trajectory Tracking Control of Self-Driving Vehicle Based on Simulated Annealing Algorithm［J］.Journal of Chongqing University of Technology:Natural Science，2015(11):106-111.