运用块体单元法的叠层梁应力分析及破坏模拟

陆晓敏，袁 涛

(河海大学工程力学系，南京 210098)

运用块体单元法的叠层梁应力分析及破坏模拟

陆晓敏，袁 涛

(河海大学工程力学系，南京 210098)

应用平面块体单元法建立由刚体位移、常应变、曲率组成的变形模式，推导了系统的平衡方程，开发了相应的数值模拟程序，计算了简支梁在均布荷载作用下的位移和应力。结果表明:在较少单元情况下位移和应力非常接近于理论解;相对于有限单元法，块体单元法的位移精度更高，一般是理论值的上限;此外，接触面中的应力精度很高，确保了模拟接触面破坏的可靠性。为模拟叠层结构变形的非线性，在块体之间的接触面内引入材料的非线性，分别考虑剪切屈服和开裂2种破坏形式。屈服判据采用M-C准则，开裂采用最大拉应力强度准则，并编制了计算机程序。最后，计算模拟了一叠层式、受均布荷载悬臂梁的应力、变形及层间剪切的破坏。结果表明:此方法能较好地模拟结构的不连续变形及破坏。

叠层梁;块体单元法;数值模拟

目前，叠层结构的复合材料在生活和工程中逐渐得到广泛应用，如家具材料中的复合板、木工板、工程结构中的复合梁等。这些材料具有层状结构，其破坏的特点常呈现层间错动和开裂、层内弯曲断裂等，与均匀连续各向同性的材料有明显的不同。所以，建立起能反映层状结构变形及破坏特点的数值模拟方法具有一定的工程应用价值。

数值模拟是力学中研究结构变形和安全度的一种有效方法。其中有限单元法［1］是最常用的一种数值方法，但其在处理层状结构时常需进行特殊处理，异常麻烦，尤其是其常用的位移模式不能很好地反映层体材料弯曲变形的特点。在块体单元法中，由于其以块体的变形为求解未知量，块体与块体之间有单独处理的接触面单元，因而在模拟非连续变形时具有一定的优势。本文据此采用块体单元法来研究叠层结构复合材料的变形、应力及破坏形态。

块体单元法的基本思想:将固体分割成块体系统，假设块体的变形模式，在块体之间人为引入接触面单元;接触面单元的变形由相邻块体的相对变形而决定;系统的平衡方程由最小势能原理导出。早期的块体单元法采用刚体位移模式，块体的变形常作简化处理。刚体位移模式的块体单元法增加了系统的刚度，求得的变形量往往偏小，因而也影响了计算的精度。有文献提出了一些简化处理的方法［2-3］，但过于简单，尤其是没有考虑材料变形的泊松比效应，给实际工程结构分析带来不少困难。

本文借鉴DDA的思想［4-5］，把块体的应变作为独立未知量，并在块体的变形模式中进一步引入曲率作为独立变量，建立起具有弯曲变形特点的块体单元法理论，并在接触面内引入材料剪切屈服和开裂的非线性模型，使之能很好地模拟层状结构的弯曲变形。此法的优点一方面能提高计算精度;另一方面，由于考虑了块体的变形，从而可以模拟材料非线性［6］的本构关系，尤其在块体单元的接触面中可以较方便地引入各种材料性质，如弹塑性、黏性流变等。本文算例表明:块体单元法理论具有较高的精度，能很方便地模拟层状结构的层间屈服、开裂的破坏过程。

1 平面块体单元法基本理论

1.1 块体的变形模式

对于平面的块体元，块体的位移和变形模式可以用3个刚体位移、3个平均应变和2个曲率来表示，用矩阵表示为

式中:ui，vi为i号块体在整体坐标系下x，y轴向的位移;θi为绕形心C的转角，在小变形的前提下这些位移是微小量;εxi，εyi，γxyi为i号块体在整体坐标下的平均线应变和切应变;κx'i，κy'i为i号块体在单元局部坐标系Cx'y'下的平均弯曲曲率，为使用方便，曲率定义在局部坐标系中。约定局部坐标系中的x'轴与单元某边平行，此方向常定义为层状结构的接触面方位。曲率与曲率半径的关系为

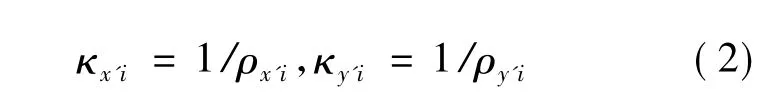
式中ρx'i，ρy'i分别为i号块体在x'和y'轴向的平均曲率半径。

如图1所示:i号块体的形心坐标用(xCi，yCi)表示;块体上某一点A的整体坐标为(xi，yi)，局部坐标为(x'i，y'i);变形前局部坐标轴x'与x轴的夹角用φi表示。在小变形假设的前提下，A点的位移可表示为

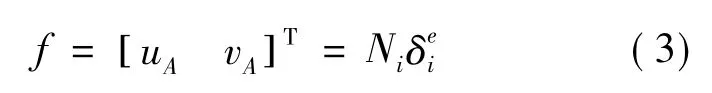
式中Ni称为块体的形函数矩阵，其各元素为:

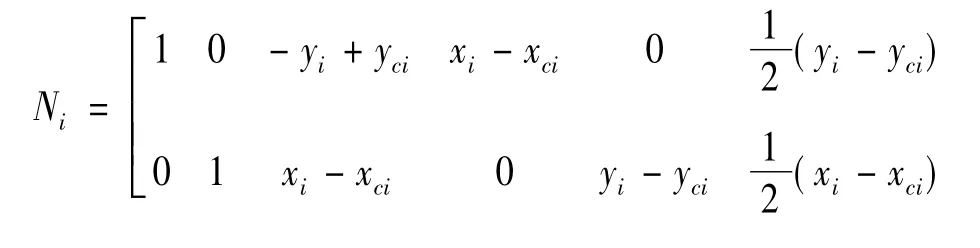
1．2 块体的应变及应力

根据式(3)可以将块体内任一点A的位移用

式中Bi称为i号块体单元应变矩阵，各元素为:

假设块体是各向同性的材料，弹性模量为E，泊松比为υ，则考虑平面应力时的弹性矩阵为

任一点A的应力为

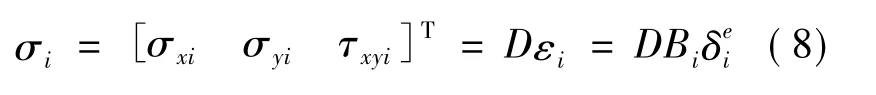
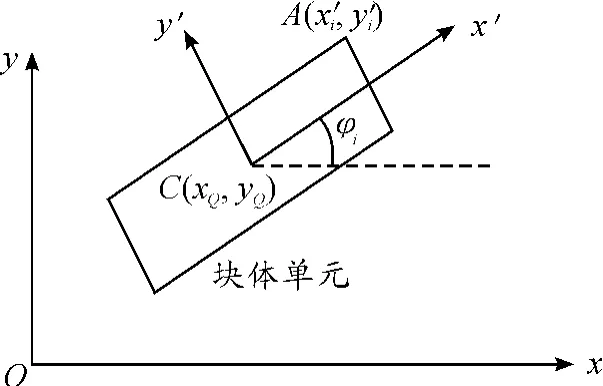
图1 块体单元与局部坐标示意图

1．3 接触面单元的应力和应变

在块体单元法中，人为在块体接触面之间引入很薄的接触面单元，见图2。设在块体i和j之间有一薄层单元(简称为接触面单元，编号为k)，厚度为h(很小)，C为形心，β为接触面单元的局部坐标x'轴的方位角。接触面上的初始接触点B和B'的位移可以用式(3)分别进行计算。

将位移转换至接触面的局部坐标系中，则

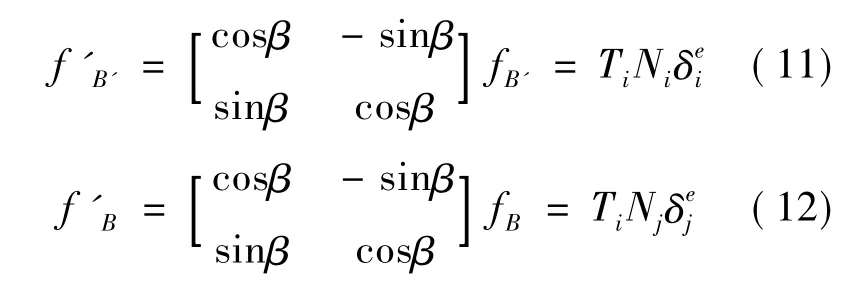
式中Ti为局部坐标与整体坐标间的转换矩阵。假设沿接触面法向(y'轴)的切应变和线应变均匀变化，x'向的线应变为块体i，j在此线应变的平均值，即

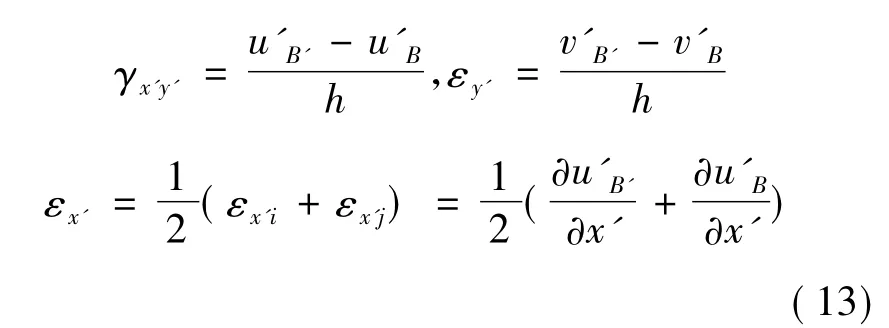
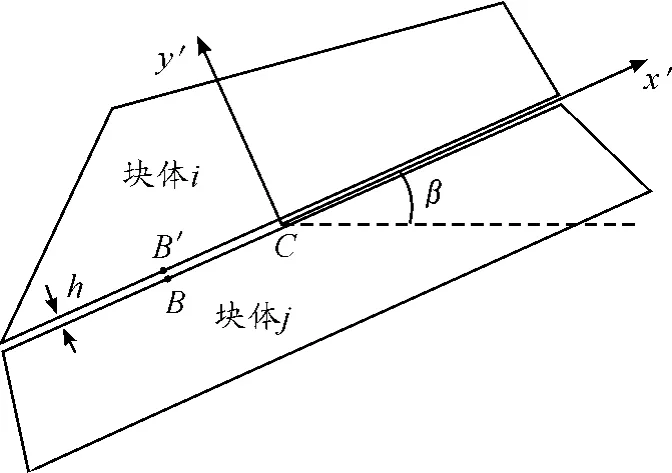
图2 接触面单元与局部坐标示意图

据此可以推导出接触面单元内的应变矩阵ε'k为

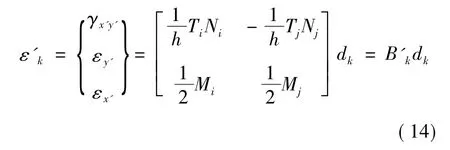
式中:(x'B'，y'B')为B'点在块体i局部坐标系中的坐标;(x'B，y'B)为B点在块体j局部坐标系中的坐标。式(14)中B'k称为k号缝面单元的应变矩阵。

假设接触面单元材料的弹性模量为E'，泊松比为υ'，引入弹性矩阵

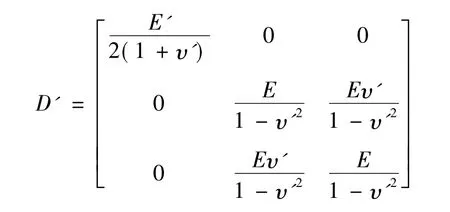
则接触面内的应力为

1．4 系统的平衡方程

系统的平衡方程可利用最小势能原理导出。系统的内力势能由块体的变形势能和接触面单元的变形势能两部分组成。块体i单元的变形势能为:

式中kBi称为块体i的单元劲度矩阵，具体计算式为

接触面单元k的变形势能为

式中kCk为接触面单元k的劲度矩阵，其计算式为

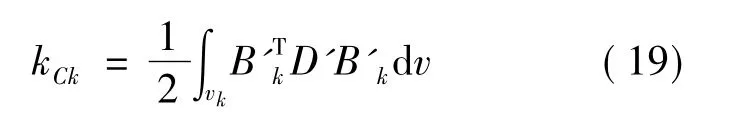
系统总的弹性变形势能为:

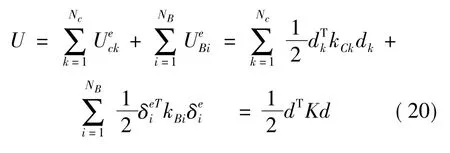
式中:Nc，NB分别为系统块体单元和接触缝面单元的个数;d为系统的未知量(位移和应变)列阵;K称为系统的劲度矩阵，由所有块体单元和接触面单元的劲度矩阵组装而成。

系统的外力势能为

式中:Fi，pi，qi分别为作用在i块体上的集中力、面力和体力矢量(矩阵);为相应的等效荷载列阵

式中:s，v分别为面力作用的面积和体力作用的体积。式(21)中R为系统的等效荷载列阵，由各块体单元的等效荷载列阵组装而成

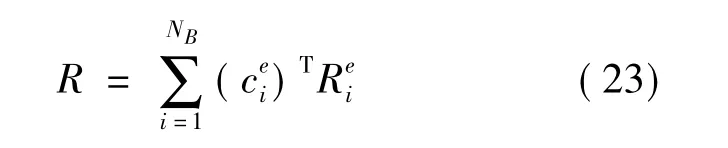
1．5 弹塑性块体单元法

在块体元模型中，既可以考虑块体材料的塑性，又可以考虑接触缝面的塑性。考虑到对于叠层梁的屈服和开裂破坏主要发生在结构面内，故本文暂只考虑缝面材料的非线性。如接触面单元屈服，则在计算其劲度矩阵和缝面应力时，需用弹塑性矩阵Dep代替弹性矩阵D'。设:缝面材料的抗拉强度为σt;抗压强度为σc;粘结强度为c;摩擦因数为f。缝面单元的破坏形式主要是剪切屈服和法向开裂，剪切屈服采用M-C准则判别，开裂由法向拉应力判别。

如果接触面单元法向应力σy'＞σt，接触面单元开裂，则认为其刚度丧失。如果

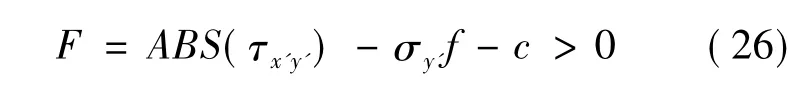
则缝面发生剪切屈服。根据相关联的流动法则可导出其塑性矩阵［7］:

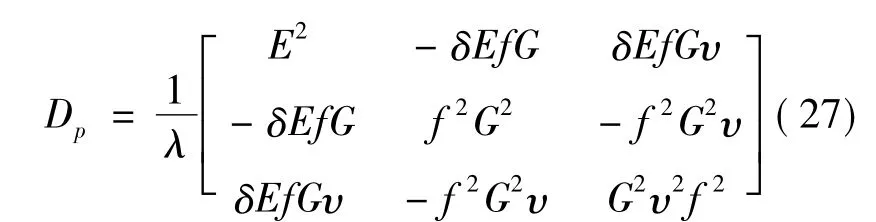
式中:λ=E+f2G，f=tanφ，δ=sign(τx'y')，E，G，υ分别为接触面材料的弹性模量、剪切模量和泊松比。

当接触缝面单元进入屈服或开裂状态后，支配方程将成为非线性方程。此时，劲度矩阵K将是位移δ的函数。为了模拟加载过程，并加快收敛速度，本文对非线性方程的求解采用子增量变刚度迭代法，在每级荷载增量中刚度矩阵保持不变，并进行迭代计算。

2 数值模拟结果

2.1 算例1:受均布荷载的简支梁的线弹性计算分析

如图3所示，取一单位厚度的矩形截面简支梁，顶部受均匀分布荷载作用。分布荷载的集度为10 kN/m2;梁的跨度为l=8 m;截面高度为h= 0.8 m。跨中截面为y轴(向下为正);中性层为x轴。梁材料的弹性模量E=2.0×104MPa，泊松比υ=0.20。计算时接触面单元厚度人为取1.0× 10-3m，网格水平方向为40等分，竖直为8层等分，块体单元的边长为0.2 m×0.1 m。

利用材料力学［8-14］的方法计算梁跨中挠度的值，本文计算的最大挠度发生在跨中，其值为6.411 1×10-3m，与材料力学法结果的误差为0.549%。块体元变形计算结果略偏大的原因主要是人为引入接触面单元降低了梁的刚度。

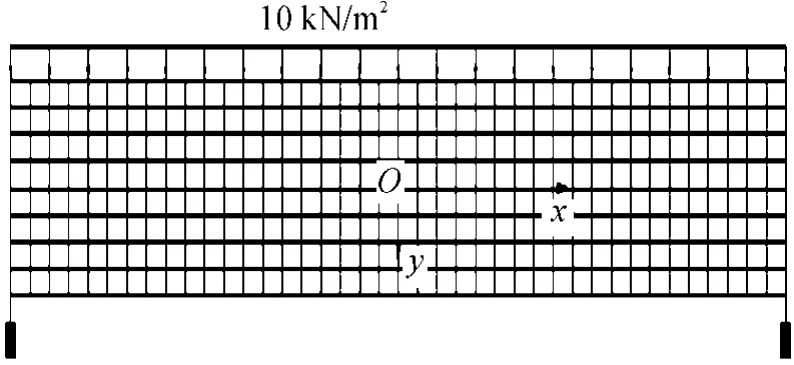
图3 简支梁网格与荷载约束图

表1给出了靠1/4跨截面处(x=-1.1 m)块体单元形心的x，y向正应力和切应力的计算值及对应的理论解［15］。比较块体元结果与理论解可以发现两者非常接近，误差不超过1.0%，说明块体元计算结果正确且精度足够。

表2给出了靠1/4跨截面处(x=-1.0 m)接触面单元形心的x，y向正应力和切应力的计算值及对应的理论解［10］。比较两者可以发现:接触面单元内的切应力及法向应力与理论解非常接近，误差不超过1.0%;但接触面方向(y向)的正应力与理论解有一定的误差，变化规律相同，最大误差为14.7%。这说明:块体元法中接触面内的切应力和法向应力计算结果可靠且精度足够，接触面内切向正应力误差略大。

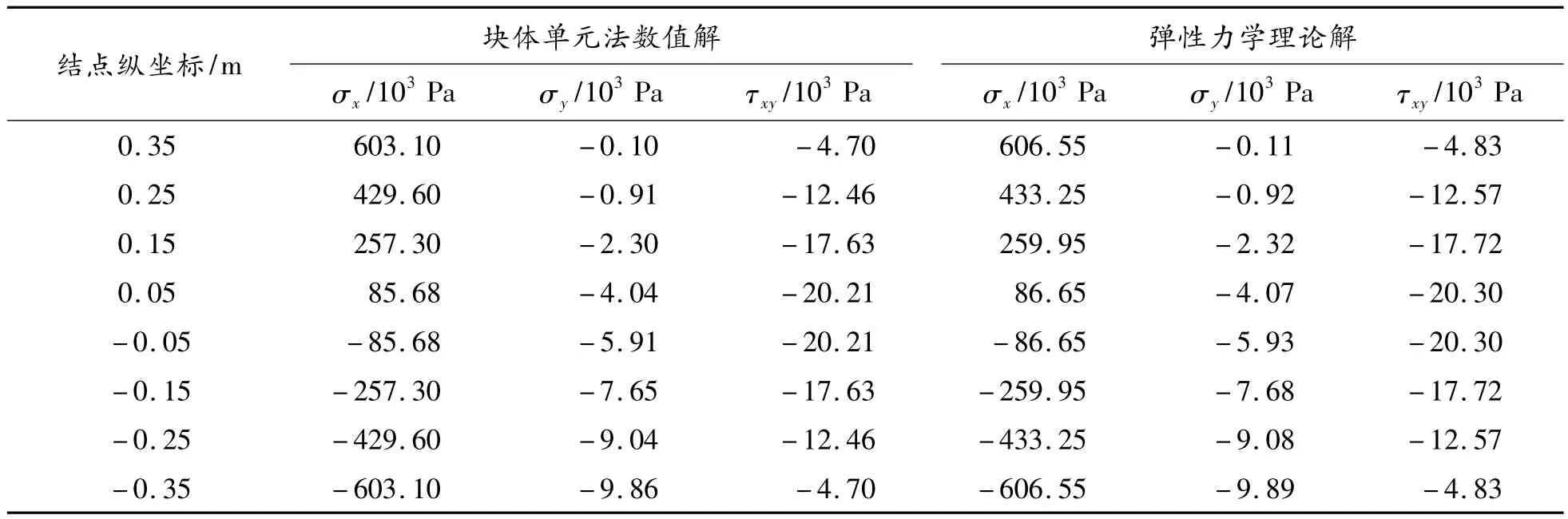
表1 截面x=-1.1 m块体形心应力分量

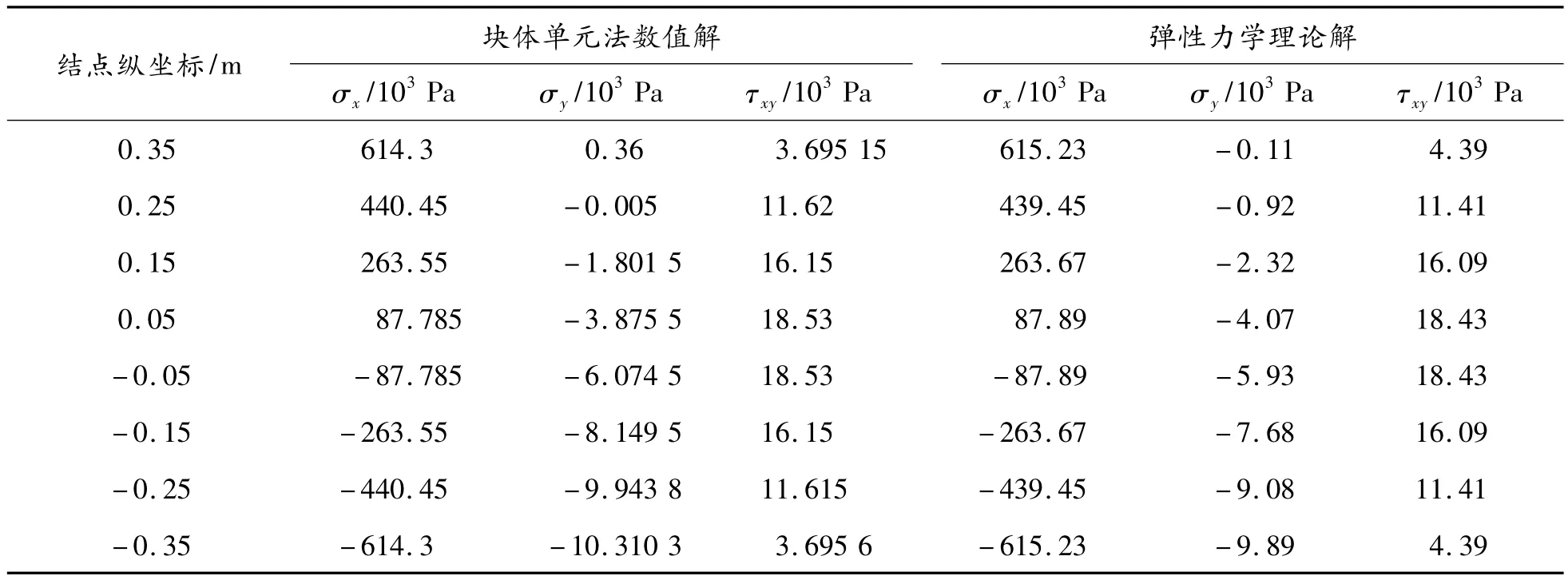
表2 截面x=-1.0 m接触缝面形心应力分量

2.2 算例2:受均布荷载的悬臂叠层梁屈服非线性分析

如图4所示，单位厚度的矩形截面悬臂梁长6.0 m，截面高2.0 m，由4层等厚的板通过粘结胶合叠加而成。网格图见图10，板材料的弹性模量均取8.0 MPa，泊松比取0.22，接触面材料弹性模量和泊松比的取值与板材一致。模拟接触面2种特性:①粘结力取0 kPa，抗拉强度取2.0 MPa，摩擦角取25°;②粘结力取300 kPa，抗拉强度取2.0 MPa，摩擦角取25°。计算时仅考虑接触面的非线性。

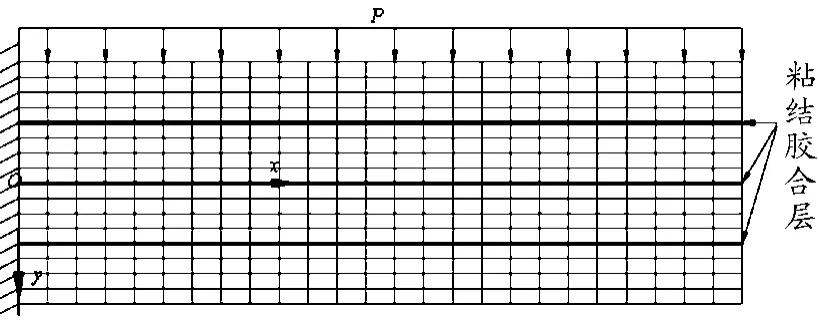
图4 悬臂梁网格荷载约束图

①属于无粘结的叠层梁问题，接触面上有法向约束力及摩擦产生的切应力。由于相对滑动，粘结面两侧的轴向正应力及位移不再连续。计算了5种荷载情况:P=30，80，120，150，200 kN/m2。图5给出了悬臂端最大挠度与荷载的关系(挠度向下定义为负值)其中:“”为整体梁计算结果(不考虑接触面的非线性);“”为叠层梁的计算结果。由变形结果可见:接触面由于摩擦屈服，梁轴向线应变沿截面高度不再连续，梁的刚度明显降低。当取均布荷载集度为150 kN/m2时，悬臂端的最大挠度分别为 -0.737 8 cm(叠梁)和-0.675 45 cm(整体梁)，叠梁的挠度增加了10.0%。图6给出梁变形后的网格图。从图6可以明显看出:粘结层处变形不连续，层与层之间有相互错动。

图5 悬臂梁端部结点位移分量与荷载图

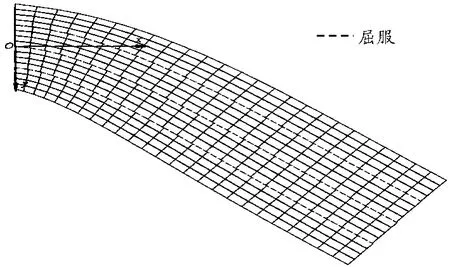
图6 悬臂梁网格变形图(P=150 kN/m2)

图7、8给出了截面A(截面位置x=4.20 m)处结点在5种不同荷载情况下的轴向正应力和切应力，数据见表3。轴向正应力图表明:由于粘结层的滑移，轴向应力在粘结层两侧不再连续;随着荷载增加，突变量也随之增加，在层内正应力基本呈线性变化。切应力图表明:在粘结层摩擦屈服后，切应力降低，不再呈抛物线变化。

图7 截面A结点正应力与荷载图

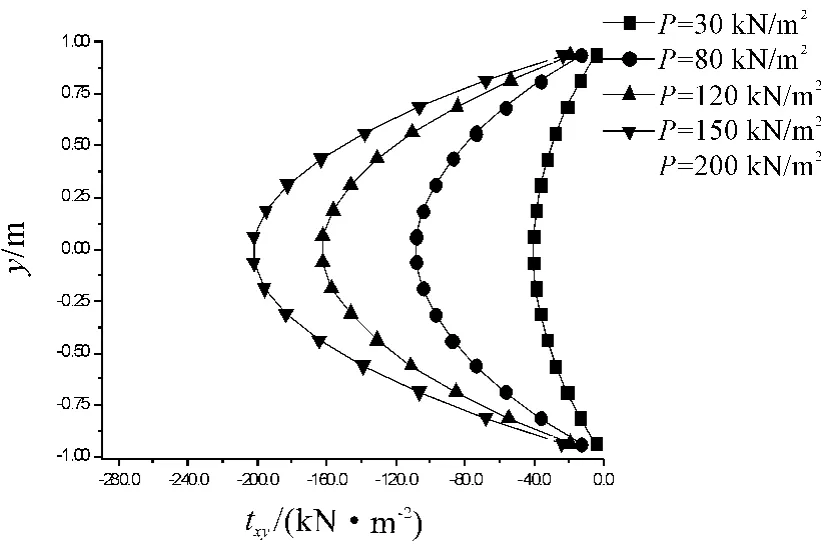
图8 截面A结点切应力与荷载图

表3 截面A(x=4.02 m)结点应力分量

②属于有粘结的叠合梁问题，接触面上有法向约束力及摩擦和粘结产生的切应力。同样计算了5种荷载情况:P=150，200，300，500，800 kN/m2。图9给出了P=150 kN/m2时叠层梁的变形及粘结层的屈服区范围。由图9可见:粘结屈服区范围及叠层梁变形比无粘结叠层梁小。由此得出:有粘结的叠层梁结构相对更稳定。

图10、11给出了截面A(截面位置x=4.20 m)处单元形心在5种荷载情况下的轴向正应力和切应力。轴向正应力图表明:粘结层一旦屈服，轴向应力在粘结层两侧不再连续，切应力也有所降低。

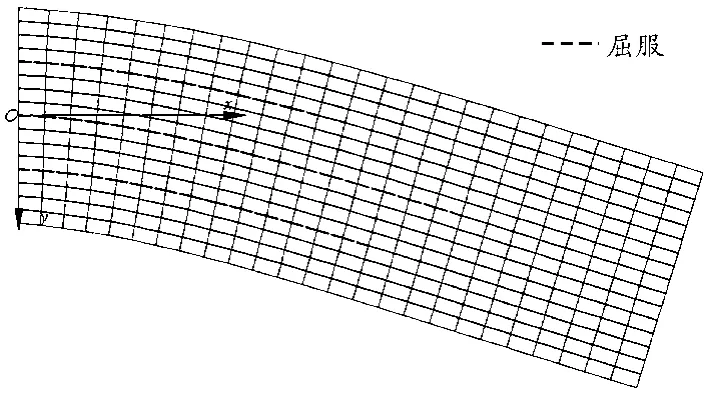
图9 悬臂梁网格变形图(P=150 kN/m2)

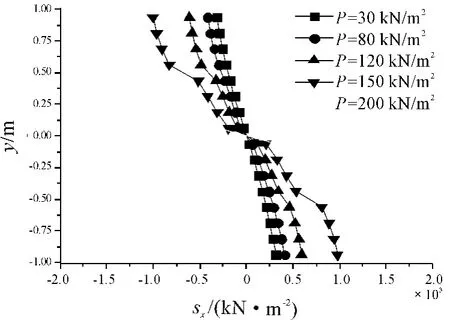
图10 截面A块体单元形心正应力图

图11 截面A块体单元形心切应力图

2.3 算例3:受集中荷载两端固定叠层梁开裂非线性分析

将上述梁的两端改为固定端约束，在第2层(从底到高编号)作用2个向下对称的集中荷载F(见图12)，网格示意图见图12。粘结面的抗拉强度取2.0 MPa，其他参数不变。随着荷载的增加，简支叠层梁中间的粘结层的最大法向应力接近材料抗拉强度，接触面层开裂。图12～14给出了3种不同荷载集度网格变形及粘结层的开裂情况。由图可知:随着荷载的逐渐增大，粘结层的开裂范围相继扩大。图15给出梁跨中底部的竖向位移分量与荷载的关系。结果表明:粘结层一旦发生开裂，梁的扰度就会发生突变。

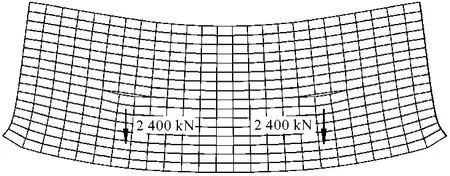
图12 荷载作用位置与网格变形图(P=2 000 kN)

图13 荷载作用位置与网格变形图(P=3 000 kN)

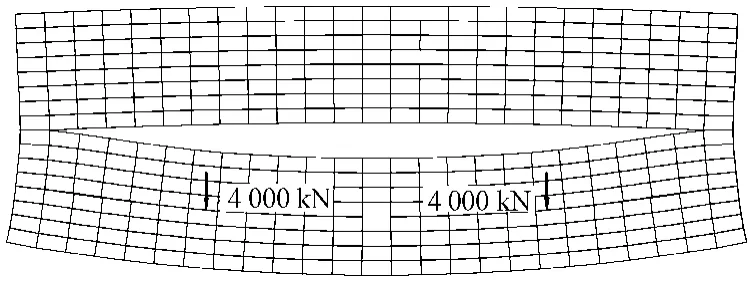
图14 荷载作用位置与网格变形图(P=4 000 kN)

图15 悬臂梁跨中底部竖向位移分量与荷载关系图

3 结束语

本文研究表明:在块体的变形模式中引入应变和曲率后能显著提高计算位移和应力的精度，且接触面的应力也有足够的精度，确保了模拟接触面材料非线性力学行为的可靠性。

考虑接触面材料的屈服和开裂后，非线性块体单元法能较好地模拟有结构面材料的非线性变形及破坏规律，如叠层复合板、层状岩体等。本文算例验证了非线性块体单元法的可靠性和合理性。如在块体内引入材料的非线性，使块体单元法模拟的结果更加接近实际。

［1］陈国荣.有限单元法原理及应用［M］.北京:科学出版社，2009.

［2］任青文，余天堂.块体单元法的理论和计算模型［J］.工程力学，1999，16(1):67-77.

［3］任青文，余天堂.边坡稳定的块体单元法分析［J］.岩石力学和工程学报，2001，20(1):20-24.

［4］石根华.数值流形方法与非连续变形分析［M］.北京:清华大学出版社，1997.

［5］陆晓敏.边坡的弹粘塑变形及稳定性研究［J］.岩石力学与工程学报，2002，21(4):493-496.

［6］殷有泉.非线性有限元基础［M］.北京:北京大学出版社，2007.

［7］李咏偕，施泽华.塑性力学［M］.北京:水利电力出版社，1987.

［8］孙训芳.材料力学［M］.北京:高等教育出版社，2003.

［9］TIMOSHENKO S P.高等材料力学［M］.北京:科学出版社，1979.

［10］陈杰.考虑层间接触变形时叠层梁层间接触压力分析［J］.力学与实践，2001(4):45-47.

［11］黄传跃，诸德超.基于剖面翘曲修正理论的复合材料叠层梁动态特性分析［J］.航空学报，1996(5):96 -101.

［12］周一勤.夹层叠层梁的内力计算及其应用［J］.华东公路，1991(5):36-39.

［13］邓梁波.地基上复合材料叠层梁的稳定性［J］.华南理工大学学报:自然科学版，1995(4):77-80.

［14］VIJAY K G.非守恒荷载作用下叠层梁的动力稳定性［J］.钢结构，2009(2):74.

［15］徐芝伦.弹性力学［M］.北京:高等教育出版社，1988.

(责任编辑陈 艳)

Analysis of Stress and Deformation of Layered Beam Based on Block Element Method

LU Xiao-min，YUAN Tao
(Department of Engineering Mechanics，Hohai University，Nanjing 210098，China)

Based on block element method，deformation mode included rigid displacement，constant strains and curvatures was constructed.The equilibrium equations were conducted by principle of minimum potential energy.The displacement and stress under blanced load of simple beam were calculated.The results of block element method show that stress and displacement are very close to theoretical values only with fewer elements，and the stresses in interface elements have more accuracy yet alway it will be the upper limit of theoretical value.Besides，the stress accuraly is very high，which can ensule the reliability in simulating the damage of the contact surface.To analyze nonlinear material mechanics，yielding and cracking in interface elements were simulated.Yielded criterion usedM-Cformulation principle and cracked condition used the principle that the max-tensile stress in interfaceelement exceeds maximum tensile strength.Using the computer program of upper method，the stress and deformation of a layered cantilever beam were studied under uniform pressure.The results are correct and show that the method of the paper is feasible.

layered beam;block element method;numerical analysis

TB301

A

1674-8425(2015)11-0051-09

10.3969/j.issn.1674-8425(z).2015.11.009

2015-06-22

国家自然科学基金重点资助项目(11132003)

陆晓敏(1963—)，男，江苏无锡人，博士，教授，主要从事水工结构、岩土工程等的力学分析及稳定性研究;袁涛(1989—)，男，江苏镇江人，硕士研究生，主要从事计算力学与工程仿真研究。

陆晓敏，袁涛.运用块体单元法的叠层梁应力分析及破坏模拟［J］.重庆理工大学学报:自然科学版，2015 (11):51-59.

format:LU Xiao-min，YUAN Tao.Analysis of Stress and Deformation of Layered Beam Based on Block Element Method［J］.Journal of Chongqing University of Technology:Natural Science，2015(11):51-59.