高中数学变式教学实践与研究

（河北省沧州市第二中学061000）

高中数学变式教学实践与研究

李园园

（河北省沧州市第二中学061000）

我国传统数学教学过程中就十分注重“变式教学”。但是在使用变式教学时，如果只是凭教学中的经验和感性认识,有时候会因为没有层次而造成理解不当，反而效果不佳，甚至会加大学生的学习负担。因此，对变式教学进行深入的研究对整个教育教学有重要的意义。

本文基于高中数学课程知识的类型,将变式教学划分为数学概念的变式教学、数学技能的变式教学、数学思想方法的变式教学。并在此基础上进行了案例分析,进一步提出了变式教学具体实践中的基本原则、具体实施形式及相应的教学策略。

一、数学概念变式教学

数学概念是最重要的数学基础知识之一，学生学习也是从学习概念开始的，通过变式教学可以让学生更清楚地了解知识的来龙去脉，从而促进概念准确的生成。数学概念变式主要包括概念的引入变式、辨析变式、深化变式和巩固变式。

（一）概念的引入变式（等比数列前n项和概念引入）

变式1：古时候，有个国王要奖励发明国际象棋的人，问他想要什么，可以满足他的任何要求。那人说：“请给我在象棋棋盘的第一格放1粒玉米，第二格放2粒，第三格放4粒，以此类推，往后每一格都是前一格的两倍，直到第64格。”国王欣然答应了。问国王真的能满足他的要求吗？想一想？

变式2：同学们，你们可以把国王需要给出的玉米数列出来吗？

变式3：如何求下列式子的值？

（1）1＋2＋22＋23＋．．＋263＝？

（2）2＋22＋23＋．．＋263＋264＝？

（3）1＋2＋22＋23＋．．＋2n＝？

（二）概念辨析变式（判断异面直线的概念）

变式1：只要不在同一个平面内的两条直线就是异面直线；

变式2：空间中只要是两条不相交的直线就是异面直线；

变式3：位于两个平面内的两条直线就是异面直线；

变式4：不平行直线和相交直线统称为异面直线；

变式5：a则a，b一定异面；

变式6：a与b是异面直线b与c是异面直线，则a与c是异面直线。变式7：如下图，正方体ABCD-EFGH中,哪些棱所在直线与直线BE是异面直线。

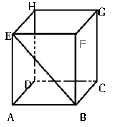
（三）概念深化变式（抛物线定义应用）

变式1：已知抛物线y2=2px上的一点M（4，m）到焦点的距离等于6，求p。

变式2：已知抛物线焦点在y轴上，顶点处在原点，且抛物线上存在一点M（3，m）到焦点的距离为5，求抛物线方程。

变式3：已知点p到直线x+4=0的距离与它到点M（2，m）的距离做差为2，求点p的轨迹方程并判断点p的轨迹是什么？

变式4：抛物线x2=8y，点A的坐标为(12，6)，点p是抛物线上的一点，，则点p到x轴的距离与点p到点A的距离求和的最小值是什么?

二、数学技能的变式教学

数学技能是在深刻理解知识的前提下经过长时间形成的一种能力，需要经过很长时间的练习，但如果只是枯燥地重复练习单一的题型，会使学生沉入“题海”从而让学生感到乏味，甚至产生逆反心理，这样反而对提高数学技能产生了消极影响。而通过变式教学，一题多变，引起学生的兴趣，使学生身临其境，愿意主动思考问题，愿意探索问题的来龙去脉，愿意主动参与到问题解决的过程中，从而抓住问题的本质特征。长期下来，变式教学使学生在形成数学技能的同时还能体验到解决问题后的成就感。

例：正弦定理变式教学

变式2：a＝2R sin A b＝2R sin B c＝2R sin C

变式3：已知在△ABC中有acos A= bcos B，判断△ABC的形状。

变式5：已知△ABC在中有sin2A=sin2B+ sin2C，判断△ABC的形状。

变式6：a:b:c=sin A：sin B：sin C

变式7：已知△ABC中三个角之比为1:2: 3，求三角形三边之比。

三、数学思想方法变式教学

在前面有关数学概念和数学技能的变式中我们已经看到了其中体现的数学思想方法。其实数学思想方法贯穿整个数学课程，它是整门课程的精华和内涵所在，不管是对数学学科各个分支的学习方面，还是对提高学生数学素养方面，还是对其他学科的学习方面，数学思想方法都起着至关重要的作用。因此，在课堂教学中，可以通过数学思想方法的变式教学让学生更加深刻地体会和运用数学思想方法。

（一）线性规划体现的数形结合思想

变式1：z=2x+y的最大值

变式2：z=x2+y2－10y+25的最小值

根据题意可作出不等式组对应的平面区域如下图：变式1：由z=2x+y，得y=－2x+z，平移直线y=－2x，由图象知当直线y=－2x+z经过点A，直线y=－2x+z的截距最大，此时z最大，由，解得，即A（1,0），此时z=2。变式

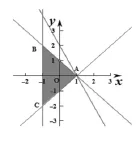
（二）函数与方程思想

变式2：过抛物线y2=2px(p＞0)的焦点F作倾斜角为45的直线交抛物线于A，B两点，若线段AB的长为8，则p=？

在教学中，如果我们能够真正深刻理解变式教学并在应用变式教学时精心设计每个环节，给学生设置适当的思维阶梯，学生会越学越轻松，越学越对数学感兴趣，那将是数学教学的一件幸事。同时，如果能在变式教学中辅助以其他教学形式（如多媒体教学），丰富课堂模式，本人觉得课堂效果将会更好，更有利于提高课堂效果。

（责编 田彩霞）