钢板局部腐蚀的脉冲涡流热成像定量检测

左宪章，胡德洲，常 东，钱苏敏

（军械工程学院 无人机工程系，石家庄050003）

铁构件广泛应用于如船舶、油气管道、发电厂、沿海工业生产等工业系统中，由于恶劣的工作环境，很容易出现腐蚀现象，进而导致穿孔、变薄等发生操作安全事故。根据腐蚀环境不同，可以将腐蚀分为两类：自然环境中的腐蚀（如空气、泥土、淡水、海水和微生物作用引起的）和工业环境中的腐蚀。根据腐蚀产生的机理同样可分为两类：化学腐蚀和电化学腐蚀。按腐蚀的形态分类，则有均匀腐蚀、电偶腐蚀、斑点腐蚀、隙间腐蚀、丝状腐蚀、晶粒腐蚀、应力腐蚀和疲劳腐蚀等［1-2］。各种腐蚀情形在钢铁设备中时常发生，对设备的使用寿命和安全都是重大隐患。因此，对腐蚀的监测和评估是至关重要的［3］。

众多基于声、热、电磁辐射的无损检测技术被应用于腐蚀的检测［4-6］，热成像无损检测最大的优点就是可以在很短的时间内快速检测大片区域的情况，检测结果直观可视，非常适合在线在役检测。涡流激励热成像就是一种以电磁激励的主动式热成像检测手段，其利用高强度的电磁脉冲对被测导体材料进行感应加热，根据电磁感应定律，当感应线圈中通入交变电流时，在置于线圈附近的导体中会产生感生涡流，当试件中存在腐蚀缺陷时，由于介质电磁特性的不连续引起产生焦耳热的不均匀分布，利用红外热像设备根据表面温度变化情况即可实现缺陷的检测［7-8］。

钢铁发生腐蚀时产生了新的物质，其物理特性也发生了相应的改变。针对钢板试件中发生局部均匀腐蚀的情况，对脉冲涡流热成像应用于腐蚀检测时腐蚀的特性进行分析，根据热成像数据对局部腐蚀的宽度和深度信息进行描述。同时利用支持向量机的良好泛化能力，引入LS-SVM（least squares support vector machine，最小二乘支持向量机）算法对腐蚀缺陷的宽度和深度二维轮廓进行重构，实现检测缺陷的定量化。

1 数学模型

脉冲涡流热成像检测涉及三个物理过程：电感线圈在导体内产生感应涡流、涡流效应产生热、热扩散。因此可以根据检测过程建立涡流场-温度场耦合分析数学模型，从而求解导体中温度场分布情况。

根据电磁感应定律，在通有交变电流的导线附近会产生交变磁场，置于磁场中的导体内将产生感应涡流。电磁场由Maxwell方程组及本征方程控制，电磁场表示为：

式中：H为磁场强度；D为电位移矢量；E为电场强度；B为磁感应强度；J为总电流密度；Js为外部电流密度；Je为感应电流密度。

引入修正矢量磁势使电场和磁场变量分离便于求解偏微分方程。

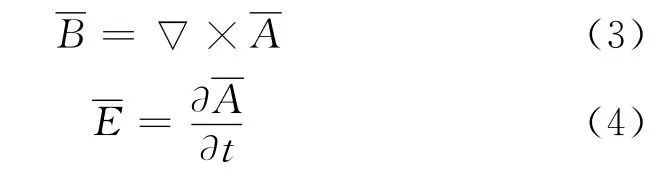
由矢量运算，对式（1）和（2）化简得到涡流场的控制方程为：

脉冲涡流感应加热激励信号为高频脉冲电流信号，根据傅立叶级数，脉冲信号可展开为奇次谐波的叠加，因此脉冲电流激励的涡流场为时谐场。涡流场控制方程用复矢量表示为：

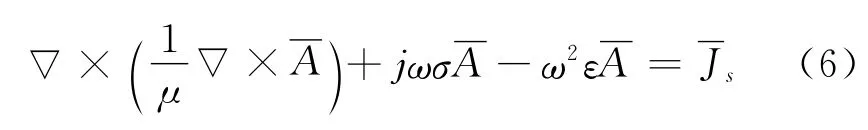
涡流场求得的感生电流产生焦耳热作为内热源来加热工件，因此导体内的涡流分布和热传导决定了导体内的温度分布。

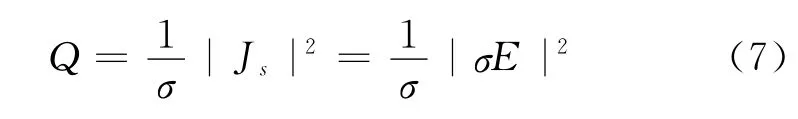
式（7）中的电导率σ跟温度有关，σ＝σ（T），关系如下：

式中：σ0为参考温度T0时电导率，α为电阻温度系数。

由于涡流为瞬态信号，且由于集肤效应，在导体中非均匀分布，因而感应加热过程属于具有不均匀内热源的非稳态导热过程，建立的方程是随时间变化的瞬态方程，温度场控制方程可由能量守恒定律和傅里叶定律建立：

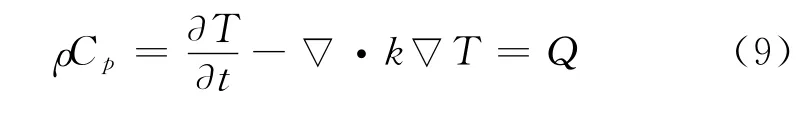
式中：ρ为材料密度（kg／m3）；Cp为材料比热容［J／（kg·K）］；k为热传导系数［W／（m·℃）］。

方程（6）和（9）的耦合求解通过有限元仿真分析软件COMSOL的AC／DC模块进行，计算感应加热时的涡流场、电磁场、温度场的分布规律。

2 仿真分析

2.1 模型建立

建立如图1所示的有限元模型，对钢板上发生局部均匀腐蚀情况下进行脉冲涡流热成像检测时的特征进行研究。试件尺寸为150mm×60mm×5mm（长×宽×高）。腐蚀区域长为30mm，宽分别为：15mm、20mm、25mm、30mm，深为0.3～0.9mm。感应线圈简化为直径4mm的长直导线，脉冲激励电流为380A，频率256kHz，加热时间200ms，冷却时间300ms。分别分析当缺陷的宽度和深度变化时试件表面的温度变化情况，讨论腐蚀尺寸与表面温度分布的关系，提取特征量对腐蚀缺陷的尺寸进行描述，分析中各单元的属性参数如表1所示。计算钢和铁锈中涡流渗透深度分别为0.059mm和0.575mm。

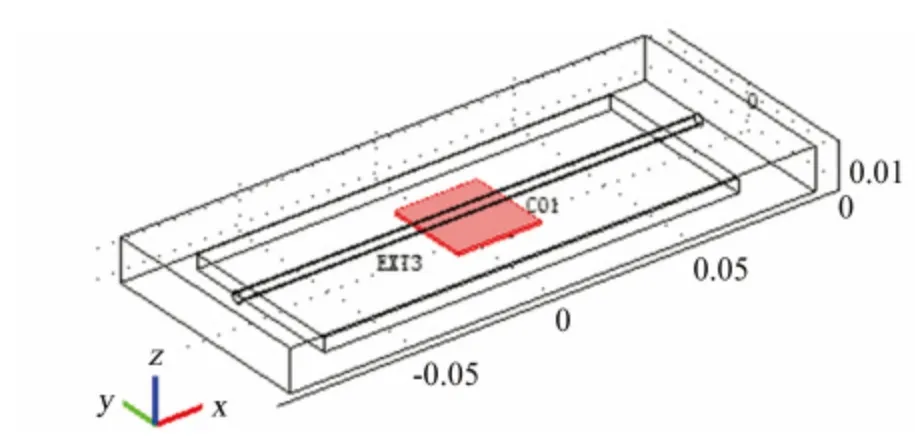
图1 3-D有限元模型Fig.1 The 3Dfinite element model

2.2 数值模拟结果分析

2.2.1 腐蚀特性分析

钢板在发生腐蚀时会产生新的物质，腐蚀主要由一系列的氧化铁（赤铁矿α-Fe2O3，磁铁矿Fe2O3和磁赤铁矿γ-Fe2O3）、氢氧化铁Fe（OH）、氢氧化铁Fe（OH）3、针铁矿（α-FeOOH）和多晶体形态）及其混合物组成［9］。它们的电导率、磁导率以及热学参数的不同将引起不同的脉冲涡流红外热成像的响应，从而使腐蚀区域与正常区域的温度分布不一样而实现腐蚀的检测。

表1 试件和腐蚀参数Tab.1 Parameters of steel and corrosion

如图2所示，分别为30mm×0.9mm腐蚀缺陷利用脉冲涡流热成像进行检测加热200ms时和冷却300ms后表面的温度分布情况。可以发现，由于缺陷区域铁锈的材料属性跟钢板本身的不一致，经过感应加热后，缺陷的温度升高值远大于钢板试件。因此，利用脉冲涡流热成像对钢试件的腐蚀情况进行检测是切实可行的，并且能够快速、直观的发现腐蚀区域。

图2 加热和冷却结束时钢板热图Fig.2 The thermal images at the end of heating and cooling of steel

2.2.2 腐蚀宽度的影响

对腐蚀深度一定、宽度变化时试件表面的温度分布情况进行分析，研究腐蚀宽度对检测的影响。以试件表面沿线圈方向中心线上的温度分布为研究对象，如图3所示为深度同为0.9mm、不同宽度腐蚀缺陷加热200ms后的试件表面温度分布轮廓。宽度为沿线圈方向中心线的腐蚀尺寸，试件长度为150mm，缺陷中心位于试件的中心，坐标为75mm处。由图可以发现，脉冲涡流激励加热后腐蚀区域的温度增加量远大于钢板无缺陷区域，而对于不同的腐蚀宽度，腐蚀区域的温度增量基本相同，即腐蚀宽度对于腐蚀区域的温度增量没有影响。

图3 宽度变化时表面温度分布Fig.3 The surface temperature distribution with width changes

对图3所示温度轮廓沿x方向做微分处理，其结果如图4所示。根据试件表面温度变化情况可以发现，由于腐蚀区域加热后温度明显高于试件本身，因此在腐蚀区跟无缺陷区域的分界处，存在一个较大的温度差，反映在差分图像中即存在明显的突变点。两突变点之间有明显温度变化的区域宽度正好对应于腐蚀区域的宽度，以此可对缺陷的边界进行识别，对于两突变点之间的有较大温度变化的区域即为缺陷区域，从而实现对缺陷宽度的判定。

图4 温度差分曲线Fig.4 The differential of temperature contours

2.2.3 腐蚀深度的影响

以腐蚀区域长宽为30mm×30mm的模型为研究对象，对腐蚀深度的影响进行分析，腐蚀深度为0.3～0.9mm，加热200ms后试件表面的温度分布轮廓如图5所示。可以发现，同一腐蚀宽度下试件表面温度较高区域的宽度相同，而腐蚀区域温度升高量随腐蚀深度的变化而改变。

图5 不同深度腐蚀加热200ms后表面温度分布Fig.5 The temperature distribution with different corrosion depth after 200ms heating

以试件表面腐蚀区域内温度上升值的平均值表征腐蚀区域的温度变化情况，对不同腐蚀深度的缺陷加热后的温度变化进行分析。如图6（a）所示，随着腐蚀深度的增加，腐蚀区域表面的温度上升值逐渐增大，而同一深度不同宽度时的温度增量相同。图6（b）为不同宽度时的温度增量取平均值跟腐蚀深度的关系，即试件表面温度最大值跟腐蚀的深度相关，而与腐蚀宽度无关。厚的腐蚀层包括更多的涡流，腐蚀层越厚，温度越高。

图6 加热200ms表面最大温度与腐蚀深度关系Fig.6 The relationship between the maxim temperature and depth after 200ms heating（a） The relationship between maximum temperature and corrosion depth for different width corrosion（b） The relationship between maximum temperature and depth

因此，对于钢板表面局部腐蚀的检测，可以根据试件表面的温度分布轮廓，以温度上升较大区域的宽度和表面最大温度值对腐蚀的深度分别进行检测。以这两个分别反映腐蚀缺陷宽度和深度信息的物理量为特征量，即可实现对试件腐蚀区域深度方向腐蚀面积的定量化检测，对腐蚀缺陷垂直切面方向的二维轮廓进行反演重构。

3 局部腐蚀试验检测

为了验证上述数值模拟结果的正确性，利用脉冲涡流热成像检测系统，分别对不同尺寸的钢板表面局部腐蚀情况进行检测，如图7所示。钢板试件上的腐蚀区域为不同面积的钢板置于自然环境中经过3～6个月的自然侵蚀形成的腐蚀区域，腐蚀区域尺寸分别为20mm×20mm×0.6mm和50mm×50mm×0.4mm。使用与数值分析相同的激励参数分别对腐蚀进行检测，热像仪帧率为200帧／s。

图8分别为两块带腐蚀钢板经过200ms的脉冲涡流激励加热后钢板表面的温度分布图像。可以发现，跟仿真分析获得的结果相似，在腐蚀区域温度的增量远高于钢板试件无缺陷区域，以板上高温区域的宽度对腐蚀宽度进行识别是可行的。而对于腐蚀深度较大的20mm×20mm的试件其腐蚀区域温度最大值6237DL高于腐蚀深度较小的50mm×50mm的钢板的5999DL，即试件表面的最大温度值跟腐蚀的深度是相关的。与数值模拟结果一致，验证了利用试件表面温度分布轮廓对腐蚀缺陷二维轮廓进行定量描述的可行性。

图7 脉冲涡流热成像腐蚀检测系统Fig.7 The system of PEC thermography detecting corrosion（a） The detection system of pulsed eddy current thermography（b） 20mm×20mm corroded plate（c） 50mm×50mm corroded plate

图8 脉冲涡流热成像腐蚀检测热图Fig.8 The thermal images of PEC thermography detecting corrosion（a） the temperature distribution of 20mm×20mm corroded plate（b） the temperature distribution of 50mm×50mm corroded plate

4 基于LS-SVM的局部腐蚀二维轮廓重构

4.1 最小二乘支持向量机

Suyken改变标准支持向量机的约束条件和风险函数，导出的LS-SVM［10-11］可以很好地应用于函数拟合问题。

用于函数估计的最小二乘支持向量机算法为：

设训练样本集为D＝｛（xk，yk）｜k＝1，2，3…N｝，xk∈Rn，yk∈R，其中xk是输入数据，yk是输出数据。在原始权w空间中的函数估计最小二乘支持向量机可描述为如下优化问题：

式中：φ（·）∶Rn→Rnh是由原始空间向高维特征空间映射的非线性函数；权向量w∈Rnh；误差变量ek∈R；b是偏差量；γ是惩罚系数，它控制对超出误差的样本的惩罚程度。

在原始权空间中，要得到的函数模型为y（x）＝wTφ（x）＋b。

在对偶空间求解函数模型，定义拉格朗日函数L：

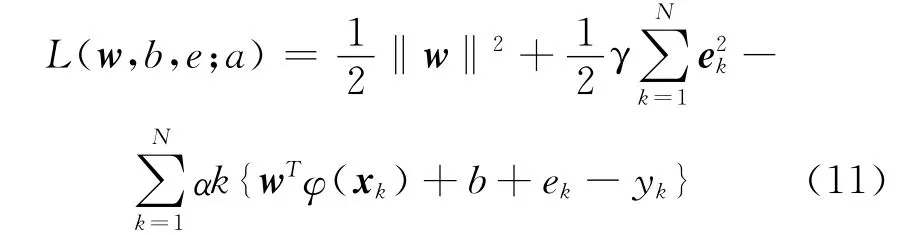
式中：αk为拉格朗日乘子。对上式进行优化，即求L对w，b，ek，αk的偏导数等于0，消除变量w和e得到矩阵方程：

式中：y＝［y1；…；yN］，lv［1；…；1］，α＝［α1；…；αn］，K＝φ（xk）Tφ（xl）＝K（xk，xl），k，l＝1，…，N。

则LS-SVM函数估计输出为：

其中b，α由方程（12）求得，K（xk，xl）为核函数。本文选择径向基函数（RBF）作为核函数，其表达式为：

参数σ2为径向基函数的核宽度，它与惩罚系数γ都对最小二乘支持向量机的估计精度和收敛速度产生影响。与标准支持向量机比较起来，LS-SVM具有更小的计算复杂性、解丧失稀疏性、能够扩展为自回归的形式来处理动态的问题的特点。另外，由于该算法采用了最小二乘法，因此运算速度明显快于支持向量机的其他算法。

4.2 样本库建立

根据对腐蚀缺陷试件表面温度场的分析，对钢板局部腐蚀试件表面温度分布轮廓而言，腐蚀宽度对信号的峰值影响很小，它主要影响高温分布区域的宽度；腐蚀的深度主要影响信号的峰值，随着深度的增加温度最大值将增大。由于这种对应关系采用表面温度轮廓为输入样本，腐蚀的深度和宽度作为输出样本，利用最小二乘支持向量机通过样本训练，建立温度轮廓跟腐蚀几何参数的非线性映射，如图9所示。

图9 腐蚀缺陷二维轮廓重构Fig.9 Reconstruction of 2-D corrosion profile

建立脉冲涡流热成像信号与缺陷特征的网络映射，需要有正确反映两者关系的训练样本和测试样本。由于制作实际腐蚀试件耗时长、成本较高，因此有限的实测数据数量不能完成样本库的建立。为了降低成本提高效率，对此采用三维有限元仿真试验的方法采集热成像信号，其中有限元仿真模型采用与实际模型相同的尺寸与参数，最终利用试验数据与仿真数据相结合方式来组成所需样本库。为了使仿真数据更加接近实测数据，仿真样本中人为的加入不同程度的非高斯噪声。

最终形成样本库共42组数据，腐蚀宽度变化范围为15～30mm，以步进值5mm递增，腐蚀深度变化范围为0.3～0.9mm。其中8组为试验数据，34组为仿真数据。重构试验中采用38组数据作为训练样本；4组作为测试样本，其中宽30mm深0.6mm为试验数据，宽15mm深0.65mm、宽20mm深0.4mm、宽25mm深0.8mm为仿真数据。测试样本与训练样本相互不重叠。

4.3 重构结果分析

以试件表面沿线圈方向的温度分布轮廓作为最小二乘支持向量机的输入，腐蚀缺陷的二维轮廓作为输出，对支持向量机网络进行训练，建立了由热成像信号到缺陷轮廓的非线性映射关系。待网络收敛后，将测试样本送入网络中检验训练效果。图10为最小二乘支持向量机重构结果。

从重构结果可以看出，使用试件表面的温度分布轮廓，可以对腐蚀缺陷的宽度和深度进行定量描述。并利用最小二乘支持向量机很好地实现了腐蚀缺陷的二维轮廓重构，而且该方法收敛速度快，不存在局部极小等问题，是一种有效可行的方法。

5 结论

图10 腐蚀缺陷二维轮廓重构结果Fig.1 0 Reconstruction results of 2-D corrosions profile

通过建立脉冲涡流热成像检测钢板表面腐蚀缺陷的有限元模型，对脉冲涡流热成像检测腐蚀时的特征进行分析，提取了利用试件表面沿线圈方向的温度分布轮廓的高温区域宽度和高温区均值为特征量，定量描述腐蚀的宽度和深度。经过试验验证，此特征量能较好地反映缺陷的几何尺寸信息。而后根据支持向量机的学习泛化能力，利用最小二乘支持向量机对样本进行训练，建立了脉冲涡流热成像信号跟腐蚀缺陷二维轮廓的非线性映射关系，实现了脉冲涡流热成像检测腐蚀缺陷的二维轮廓重构。

［1］WINSTON R R，HERBERT H U.Corrosion and corrosion control，An introduction to corrosion science and engineering［M］.Hoboken New Jersey.John wiley ＆Sons，Inc.，2008.

［2］HOU W，LIANG C.Atmospheric corrosion prediction of steels［J］.Corrosion，2004，60：313-322.

［3］张鹏，蒋健，严东洲.基于风险检测技术在某海上油气田装置腐蚀风险预测的应用［J］.腐蚀与防护，2013，34（4）：346-350.

［4］JÖNSSON M，RENDAHL B，ANNERGREN I.The use of infrared thermography in the corrosion science area［J］.Materials and Corrosion，2010，61：961-965.

［5］HAN J S，PARK J H.Detection of corrosion steel under an organic coating by infrared photography［J］.Corrosion Science，2004，46：787-793.

［6］HE Y，TIAN G，ZHANG H，et al.Steel corrosion characterization using pulsed eddy current systems［J］.IEEE Sensors Journal，2011，12：2113-2120.

［7］常东，左宪章，田贵云，等.裂纹方向对脉冲涡流热成像的影响［J］.上海交通大学学报：自然版，2013，47（5）：779-785.

［8］VAVILOV V P.Non-contact one-sided evaluation of hidden corrosion in metallic constructions by using transient infrared thermography［J］.Revista de Metalurgia（Madrid），2003：235-242.

［9］DE LA FUENTE D，DÍAZ I，SIMANCAS J，et al.Long-term atmospheric corrosion of mild steel［J］.Corrosion Science，2011，53：604-617.

［10］SUYKENS J A K.Least squares support vector machine classifiers［J］.Neural Processing Letters，1999，9：293-300.

［11］SUYKENS J A K，VANDEWALLE J，MOOR B.Optimal control by least squares support vector machines［J］.Neural Networks，2001，14：23-35.