基于有向加权复杂网络的自适应粒子群算法

黄 珍，曹晓丽

(兰州文理学院数字媒体学院，甘肃 兰州 730000)

粒子群优化算法(Particle Swarm Optimization，PSO)是一种基于群体智能的随机优化算法［1］.该算法类似于鸟群觅食行为，通过种群内部信息共享和个体间相互协作来搜索得到问题的最优解.鉴于算法具有容易实现、计算速度快、可以并行处理等优点，粒子群优化算法在神经网络训练、函数极值估计、人脸检测与识别等领域已经得到成功的应用［2-4］.

在高维空间寻优迭代过程中，标准粒子群优化算法存在后期收敛速度慢和易陷入局部最优的问题，目前已经有很多学者对其进行改进，如文献［5］利用不同邻域结构的粒子群优化算法进行函数极值估计，在一定程度上提高了粒子寻优性能.然而，不同问题粒子群的拓扑结构也不一样，算法开始很难选择最佳的粒子群拓扑结构，因此该算法的适应性较差.文献［6］利用无标度网络拓扑结构的一些特性来优化粒子群算法，使其在高维空间寻优能力上有了进一步的提高，但无标度网络并不一定是最优的拓扑结构.文献［7］提出了一种自适应的多向学习粒子群优化算法，群体中的每个粒子不仅比较自身最优解和整个群体的最优解，同时还随机和其他同维度的粒子最优解相比较，从而完成自身速度的更新.该算法在解决高维优化问题时有了进一步的提高，但没有考虑粒子寻优的网络拓扑结构，不同的邻域网络拓扑结构对粒子群的最终寻优结果有很大影响.

全局耦合网络中的每个节点之间都有边连接［8］.作为基本粒子群的网络邻域结构，网络中的每个节点(位置)都将与网络中的其他所有节点(位置)相比较，从而选择最优的粒子进行学习.在所有网络拓扑中，具有相同节点数的全局耦合网络具有最大的集聚系数(C =l)和最小的平均路径长度(L =1)［9］.然而在高维空间解中，传统PSO 更容易陷入局部最优.在全局耦合网络邻域结构中，粒子寻优能力差以及寻优方式呆板，小世界网络模型邻域结构作为PSO 寻优邻域初始化有较好的表现.本文提出利用小世界网络模型邻域结构对PSO 进行初始化，由于其邻域结构中每个粒子仅仅与网络中的邻居位置进行比较，所以算法的收敛速度将进一步提高，网络中的每个粒子都能保持寻找最优的解(即粒子群中解的多样性)，在可接受的误差范围内，小世界网络作为粒子群的邻域结构具有较好的优化效果.尤其在解决高维复杂函数问题时，小世界网络邻域结构效果更为明显.PSO 算法最终收敛时，其粒子邻域结构的节点入度服从幂律分布［10］，因此可以把无标度网络作为粒子最终收敛时的粒子邻域结构.基于以上内容，本文提出小世界网络模型向无标度网络模型进化的动态粒子邻域拓扑结构.

本文将复杂网络中小世界网络模型和无标度网络模型的网络特性融入到粒子群优化算法中，提出有向加权复杂网络的粒子群优化算法(Directed Weighted Complex Network Particle Swarm Optimization，DWCN -PSO).仿真结果表明，DWCN -PSO 算法尤其在高维空间寻优时，性能及收敛速度都比标准PSO 有所提高.

1 基本粒子群优化算法

粒子群优化算法最初是从社会行为的模拟发展起来的具有全局搜索能力的智能群体算法［11］.在一个n 维的目标搜索空间中，粒子群被初始化分布在空间中，每个粒子所在空间的位置表示一个具体问题的解，系统中的每个粒子在目标搜索空间中寻找最优粒子的位置.假设系统中粒子的数目被初始化为N 个，第i 个粒子的位置由一个n 维的向量来表示，即xi= (xi，1，xi，2，…，xi，n)，i = 1，2，…，N，其中xi，j∈［aj，bj］，即aj≤xi，j≤bj．i = 1，2，…，N;j = 1，2，…，n.粒子的每一个位置对应问题域中的一个潜在解.粒子xi的适应值代表一个具体问题的潜在解，不同的适应值表示解的优劣性.一个n 维的向量表示为粒子i 的速度，即vi= (vi，1，vi，2，…，vi，n)，i = 1，2，…，N.pi= (pi，1，pi，2，…，pi，n)，i =1，2，…，N 表示为粒子i 到目前为止寻找到的最优值，pg= (pg，1，pg，2，…，pg，n)，i = 1，2，…，N 表示为粒子群到目前为止找到的全局最优值，粒子群优化算法采用(1)式和(2)式进行寻优操作:

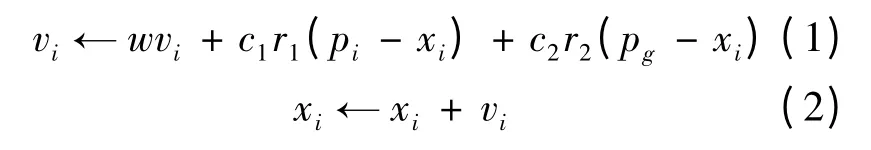
其中，i = 1，2，…，N;r1和r2是属于［0，1］范围内的随机数;c1∈［0，2］和c2∈［0，2］表示为两个学习因子.算法的最大迭代次数根据问题的具体情况进行设置或者设置成为迄今为止寻优到的最佳位置且满足预定阈值时的次数.在高维空间寻优迭代过程中，标准粒子群优化算法存在后期收敛速度慢和易陷入局部最优的问题，如果采取一些优化方法进一步提高粒子的拓扑结构，无疑会提高粒子群优化算法的性能.

2 有向加权复杂网络的自适应粒子群优化算法

2.1 粒子群有向加权复杂网络模型

网络模型具体构建如下:

定义1 设复杂网络G = {V，E，W}，V 为顶点的集合，E 为边的集合，W 为边上权重的集合．A 为复杂网络G 的邻接矩阵，A = (aij)n×n．其中，aij表示节点i 和节点j 的连接关系:如果这两个节点之间有边相连，则aij为1，否则为0．W =(wij)n×n为网络边上权重矩阵，其中wij为边aij上的权重．

节点i 的加权出度为:

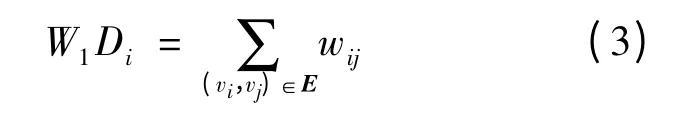
节点i 的加权入度为:

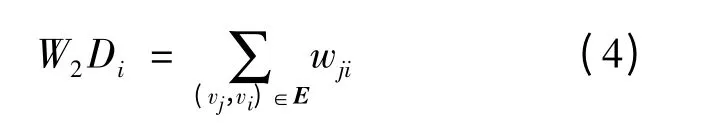
邻接矩阵A 为:

此时以一定的概率p 连边，0 ＜p ＜1 ．其中:i =1，2，…，N;j = 1，2，…，N．i ≠j．D(xi，xj)表示两粒子之间的欧氏距离，R 表示粒子之间欧氏距离邻居阈值，f(xi)表示粒子的适应值，V(f(xi)，f(xj))表示粒子i 与粒子j 的适应值之差．

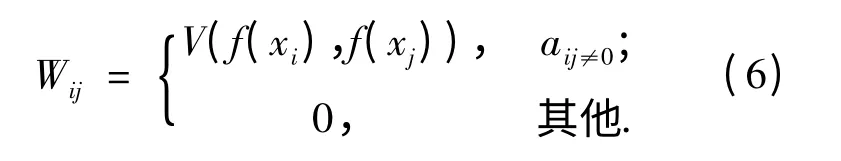
对网络边的权值进行归一化，即:

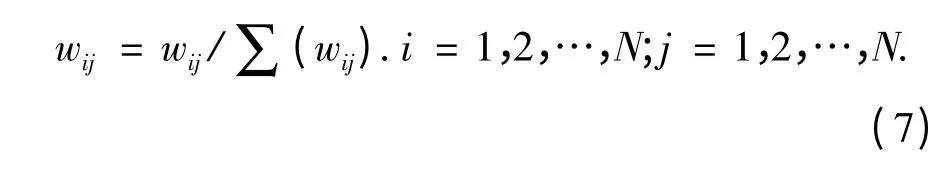
∑(wij)表示边上权值和;权值归一化后，0 ≤wij≤1 ．

2.2 粒子自适应寻优

把2．1节中构建的复杂网络模型引入到粒子群寻优的网络拓扑邻域结构中，考虑一个有向的小世界网络到无标度网络动态的演化过程．当粒子最终收敛到最优时，节点的入度服从幂律分布．在粒子群每次迭代过程中，粒子的网络拓扑在入度服从幂律分布的条件下动态进行改变．本文粒子之间学习方式按以下3 个原则:

(1)采用最优邻居(位置)的方法进行粒子寻优．

网络中的每个粒子在寻找自身最优(pbest)位置的同时也向邻居们的最优(lbest)位置学习．当粒子i 与粒子j 之间位置相距很近时，比如小于某阈值R 时，两粒子互为邻居，另外当粒子i 与粒子j 之间位置大于某阈值R 时，此时以一定的概率p(0 ＜p ≪1)互为邻居(可视为虚拟邻居)．

(2)随机连接到非粒子连接邻域的其他粒子(虚拟邻居)．这样可以当粒子陷入局部最优时有效跳出局部最优值．

每个粒子在自身邻居内寻优，当粒子i 与粒子j 之间位置大于某阈值R 时，此时以一定的概率p(0 ＜p ≪1)互为邻居(可视为虚拟邻居)，这样当粒子在空间距离阈值R 内找不到最优邻居时可以有效地跳出局部极值，从而自适应寻找全局最优值．

(3)在粒子学习最优邻居的过程中引入动态学习因子c2，使粒子的飞行惯性在空间上也是异质的．这样可以增强粒子之间学习的多样性，避免粒子在高维空间寻优时陷入局部最优．

本文算法中粒子除了学习自己最优位置外只向最优邻居位置学习，此时的邻居也包括虚拟邻居．当粒子i 的邻居很多时，只选取邻居中的最优粒子作为连边邻居，两粒子的边为aij，边上的权值wij为两粒子适应值之差．两粒子的适应差越大，粒子i 学习最优邻居粒子j 的位置越迫切．在公式(1)中引入动态学习因子c2和变惯性权重w，使得粒子的飞行惯性在时间上和空间上都是异质的．改进公式:

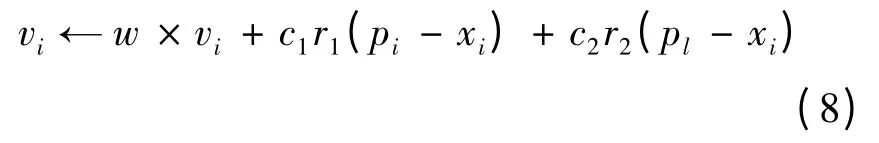
其中i = 1，2，…，N，w = (w1- w2)× (T -iter)/T+w2;w1和w2表示为惯性权重的初始值与终值;T 为迭代的最大次数;iter 代表当前的迭代次数;c2= (1 + wij)c1;wij为归一化后的边权重;pl为最优邻居位置．

粒子的加权入度W2Di代表邻居粒子向该粒子学习的程度，粒子的加权出度W1Di代表该粒子向其他邻居粒子学习的程度，有向加权复杂网络中的节点加权入度W2Di为n，n ≥0 ，加权出度W1Di为1 或0(只向最优邻居粒子学习或没有最优邻居粒子而不学习)．当粒子群算法收敛时，网络中节点入度服从幂律分布且当网络中粒子的最大加权入度W2Di大于某一阈值K 且加权出度W1Di为0 时，此时粒子找到最优值．在这种拓扑结构的变化中，由于每个粒子都向自己最优邻居的位置进行学习，从而使网络中的节点入度服从幂律分布特征且有较大的异质性．同时，这种随机连边的操作使得陷入局部最优的粒子能够跳出局部极值飞向非连接邻域中的其他粒子位置．由于这种改进是基于有向动态邻域结构的，所以粒子可以自适应找到最优值．

有向加权复杂网络的自适应粒子群优化算法具体步骤如下:

Step 1:确定学习因子c1、c2，随机边连接概率p，群体规模N，惯性权重的初始值w1与终值w2，粒子群进化次数T.

Step 2:对粒子群中各粒子的位置和速度进行随机初始化且控制在一定范围内.

Step 3:初始化粒子群网络邻域:计算每个粒子的适应值f(xi)及其间的欧氏距离D(xi，xj)，按照2.1 中提出的复杂网络模型对粒子群构建复杂网络邻域结构，计算对应的邻接矩阵A 和网络边权重矩阵W.

Step 4:计算每个粒子的适应值f(xi)，和它自身到目前为止找到的最优值pi进行比较.如果pi没有该粒子的当前适应值好，则使pi等于当前适应值;对每个粒子的适应值f(xi)和邻居最优值pl进行比较，如果pl没有该粒子的当前适应值好，则使pl等于当前适应值.

Step 5:在网络邻域入度服从幂律分布的条件下所有粒子按照(8)式和(2)式寻优;当粒子速度及位置越过搜索边界时，自动取边界值;计算寻优后的邻接矩阵A 和网络边权重矩阵W;对粒子群中原有的网络邻接矩阵A 和网络边权重矩阵W 进行动态更新.

Step 6:检查是否满足终止条件(计算粒子群复杂网络中节点的最大加权入度W2Di和该节点的加权出度W1Di.当最大加权入度W2Di大于某一阈值K 且加权出度W1Di为0 时，此时粒子找到最优值).若是，则终止算法;否则转Step4.

3 仿真实验

实验软件平台为 Windows 7 和 Matlab R2010a，硬件平台为CPU Intel Core i5，内存4 GB.测试函数如下:

参数设置:粒子群规模N =30，最大迭代次数Interation_max = 100，学习因子0 ＜ c1＜混沌系统的初值为x=0.1，y= -0.2.DWCNPSO 中wmax= 0．9 ，wmin= 0．4 ，p = 0．1 .把DWCNPSO 算法分别和PSO 和基于Cat 混沌映射的SFPSO 算法进行对比分析.仿真结果如表1所示.

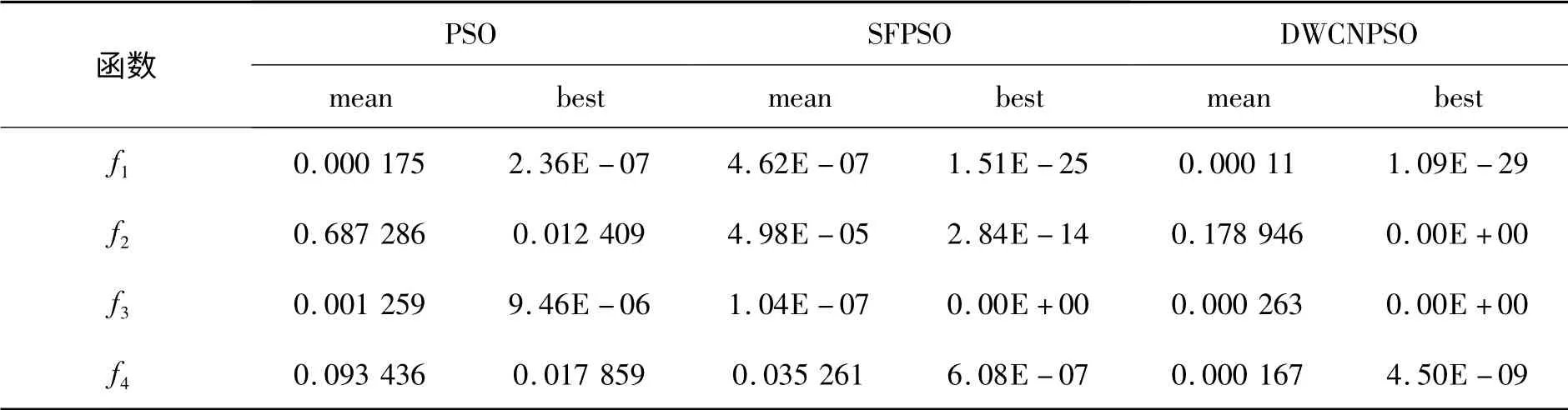
表1 4 种算法测试仿真结果比较

(1)基于其他网络拓扑邻域的PSO 比较:

由表1可知，对于函数f1、f2和f3来说，本文算法的最优值优于其他所有算法，但没有SFPSO算法的平均值好.对于函数f4来说，本文算法的平均值和最优值要优于其他所有算法.从整体可知:PSO 算法的性能最差，本文算法的最优值性能好，本文算法比其他算法更易找到全局最优值.

图1是4 种算法对测试函数的寻优迭代曲线.为了更清晰地表达寻优结果，对适应值取以e 为底的对数.由图1(b)可知，SFPSO 算法和PSO 算法在迭代次数为10 的时候就陷入了局部最优且迭代多次粒子仍不能自动跳出局部极值，而本文算法不仅不易陷入局部极值而且收敛速度也比其他两种算法快，在4 个测试函数中本文的算法都能够找到最小值且在算法陷入局部最优时，仍能够通过随机连边操作自动跳出局部最优，在搜索精度和收敛性能上本文算法都是最好的.函数f1和f2用来测试算法能否找到全局最优值，函数f3和f4用来测试算法能否在多个局部极值点的干扰下找到全局最优值.由图1(b)可知，本文算法的搜索精度最高，找到了全局最小值;由图1(d)可知，本文算法较好地平衡了全局和局部搜索，不易陷入局部最优且收敛速度较快，并找到全局最小值.

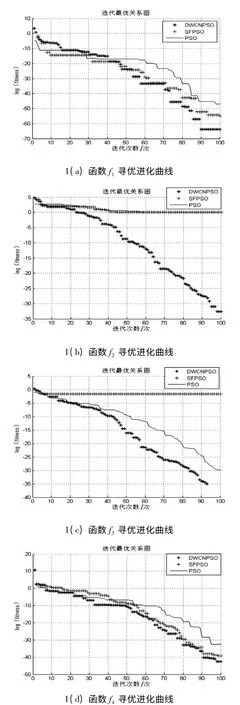
图1 3 种算法对测试函数的寻优迭代曲线

(2)网络平均度对DWCNPSO 的影响

由上文实验结果可知，粒子群邻域网络的拓扑性质对算法的寻优结果有很大影响.对于同一种网络，为了研究拓扑性质的差异是否对PSO寻优结果有一定的影响，本文以无标度网为例，对PSO 粒子寻优结果进行分析.在无标度网络中，不同的网络平均度代表着不同的网络拓扑结构［12］.下面对基于无标度网络邻域拓扑的不同网络平均度的PSO 效果进行分析.对Rosenbrock和Rastrigrin 函数进行多次实验(200 次重复独立的随机实验)，测试结果如图2所示.对Rosenbrock 目标函数来说，在平均度为〈K〉 =6.01 与〈K〉 =7.85 的情况下粒子寻优较好，而当〈K〉 =10.23 时粒子寻优时陷入了局部最优，因此网络平均度值的增加对Rosenbrock 函数的测试结果并不一定越好，而对Rastrigrin 函数来说平均度〈K〉 =10.23 时，寻优效果最佳.对于2 个目标函数而言，PSO 在一个平均度值范围内，网络上的粒子寻优效果最佳.

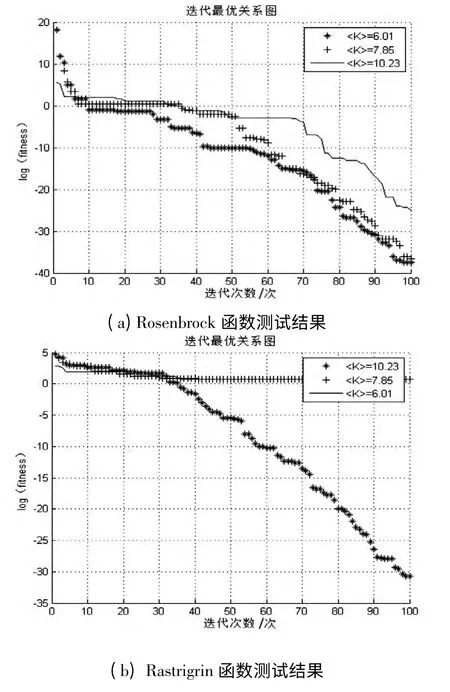
图2 两种算法对测试函数的寻优迭代曲线

4 算法分析

4.1 算法收敛性分析

基本粒子群优化算法在迭代到最后都能满足收敛条件，文献［13］证明了该算法是收敛的.当公式(1)中w ＜1、c ＞0 且c = c1+ c2、2w -c +2 ＞0 时，基本粒子群算法是收敛的，收敛区域如图3所示.本文算法是通过构建粒子群复杂网络以及增加自适应学习因子c2来对基本粒子群优化算法进行改进，算法的搜索机制并没有改变.在本文算法中c = c1+c2= c1+(1 +wi，j)c1=(2 +wi，j)c1，由于0 ＜c ＜2w +2 ，所以当0 ＜c1时，本文所提出的算法也是收敛的，从上面的实验结果可知，本文算法不仅收敛而且收敛速度有很大的提高.

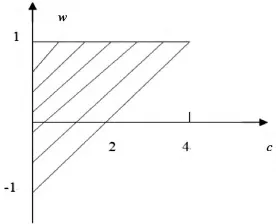
图3 基本算法参数收敛区域

4.2 算法复杂度分析

衡量一个算法优劣的一个重要指标就是时间复杂度［14］.假设粒子群搜索空间维数为D，粒子数目记为N，粒子群迭代的最大次数记为T.在标准粒子群优化算法中，粒子位置的初始化以及速度的初始化分别为O(ND)，计算粒子适应值的时间复杂度为O(N2)，对粒子位置以及速度进行更新操作的时间复杂度分别为O(ND).在本文算法中，由于初始化粒子群时引入了小世界网络模型且构建有向加权复杂网络的时间复杂度为O(N2)，本文算法在时间上有所增加.然而，本文算法能够较好解决高维空间求解问题，并且在算法陷入局部最优时，仍能够通过随机化连边操作跳出局部最优值.在高维空间寻优迭代过程中，对于标准粒子群优化算法所带来的后期收敛速度慢和易陷入局部最优的问题相比，构建复杂网络的时间是可以接受的.在实际应用中，复杂问题的搜索空间维数都比较大，此时本文算法更具有优越性.

5 结语

本文提出的基于有向加权复杂网络的自适应粒子群优化算法，通过引入复杂网络模型以及动态学习因子，提高了粒子之间学习的多样性，从而使粒子能够快速找到最优解，并且在算法陷入局部最优时，仍然能够通过随机化连边等操作较快地跳出局部最优，进而飞向全局最优.在算法复杂度上，对于标准粒子群优化算法所带来的后期收敛速度慢和易陷入局部最优的问题相比，构建复杂网络的时间是可以接受的.在实际应用中，复杂问题的搜索空间维数都比较大，而粒子数目一般设置为N(N ＜50 )，此时本文算法更具有优越性.仿真实验结果也表明，本文算法与标准粒子群算法以及基于Cat 混沌映射的SFPSO 算法相比较，具有更好的搜索精度且不易陷入局部最优，尤其在高维搜索空间寻优过程中，本文算法搜索后期具有较快的收敛速度.

［1］Kennedy J，Eberhert R.Particle swarm optimization［C］.IEEE International Conference on Neural Networks，1995:1942 -1948.

［2］吴正科，杨青真，施永强，等.带粒子释放和速度限制的粒子群算法［J］.计算机应用研究，2013，30(3):682 -685.

［3］Alfi A.Particle swarm optimization algorithm with dynamic inertia weight for online parameter identification applied to Lorenz chaotic system［J］.International Journal of Innovative Computing，Information and Control，2012，8(2):1191 -1203.

［4］李朔枫，李太勇.一种基于距离的自适应模糊粒子群优化算法［J］.计算机科学，2011，38(8):257 -259.

［5］Kennedy J.Small worlds and mega - minds:effects of neighborhood topology on particle swarm performance［C］.Proceedings of 1999 Congress on Evolutionary Computation.Washington D.C.，USA 1999.

［6］姚灿中，杨建梅.静态与动态SF 拓扑邻域对PSO 改进算法的分析［J］.小型微型计算机系统，2012，33(5):1113 -1116.

［7］阚超豪.多向学习自适应的粒子群算法［J］.计算机工程与应用，2013，49(6):23 -28.

［8］朱大勇，张新丽，李树全.利用局部拓扑信息发现模糊社团结构［J］.电子科技大学学报，2011，40(1):73 -79.

［9］Jiménez，Abigail.A complex network model for seismicity based on mutual information［J］.Physica A:Statistical Mechanics and its Applications，2013，392(10):2498 -2506.

［10］Qu Kaiming，Peng Haipeng，Fu Peilu，et al.Topology identification of complex network via fast converging particle swarm optimization algorithm［J］.Journal of Nanjing University of Science and Technology，2012，36(2):84 -89.

［11］Gutierrez A L.Comparison of different pso initialization techniques for high dimensional search space problems:a test with FSS and antenna arrays［C］.Proceedings of the 5th European Conference on Antennas and Propagation (EUCAP)，2011:965 -969.

［12］Zhu Zhiliang，Lin Sen，Cui Kun，et al.Network topology layout algorithm based on community detection of complex networks［J］.Journal of Computer -Aided Design and Computer Graphics，2011，23(11):1808-1815.

［13］申元霞，王国胤，曾传华.PSO 模型种群多样性与学习参数的关系研究［J］.电子学报，2011，39(6):1238 -1244.

［13］胡旺，张鑫.一种基于进化过程学习的粒子群优化算法［J］.计算机科学，2012，39(4):193 -195.