基于含公平偏好约束集的DEA 固定成本分摊方法

宋美英

(西南大学数学与统计学院，重庆 400715)

一般来说，企业的生产活动是多个生产要素共同作用的结果，对各生产要素投入的多与少直接影响到企业各利润的组成，因此进行固定成本分摊时需综合考虑这些生产要素的消耗及消耗之后所带来的利润.DEA(数据包络分析)是一种非参数的估计方法，它通常采用加权的办法综合投入指标值和产出指标值以评价一组具有多投入多产出的同质决策单元(DMU)的相对有效程度.所以，DEA 方法可以有效应用于多种生产要素相关联的固定成本分配问题.本文考虑的固定分摊是指组织为组织内各子决策单元在建公共平台上所花的费用.当建立公共平台的费用超出预算内费用时，超出的费用如何在各子决策单元内分摊.

对于DEA 方法在固定成本分摊问题中的应用，文献［1 -3］均有相应研究，特别在文献［2］中，李勇军总结了前人所研究的DEA 模型在固定成本分摊中的应用，并进行相应的改进，提出基于联盟博弈的DEA 方法，认为一种投入要素的增加必定会引起另一种投入要素的减少，从而给出固定成本分摊的Nash 讨价还价模型、核仁解模型等，进一步拓展了DEA 方法在固定成本分摊中的应用.

文献［2，4 -8］中出现的模型，对于固定成本分摊这一问题来说，会导致所得的成本分摊方案出现两个问题:(1)由于DEA 对优势指标的偏爱，导致劣势指标输入、输出指标权重为0，这意味着可以忽略该指标对利润输出的影响，而成本分摊时各指标对于生产活动缺一不可，需综合考虑;(2)忽略了决策者的偏好，在生产活动中，各生产要素重要性不同，而DEA 方法认为各指标同等重要.为解决以上两个问题，本文提出了一种含有公平偏好约束集的DEA 固定成本分摊模型.

1 预备知识

1.1 固定成本作为新投入要素的分摊模型

假定固定成本分摊可以作为决策单元的一个新投入要素，那么在效率评价过程中考虑固定成本因素，单个DMU 关心的是:什么样的分摊方案才能使自己在成本分摊后的相对效率达到最大，以及到底能达到多大.如果从整体效率评价角度出发，决策者最为关心的是什么样的分摊方案才能使得整体在成本分摊后相对效率达到最大，以及到底能达到多大.

假设有n 个决策单元，每个决策单元组织m种资源生产s 种产品.输入指标权重向量记为:v = (v1，v2，…，vm)T，输出指标权重向量记为:u = (u1，u2，…，us)T;输入、输出向量值分别为:xij，yrj(i = 1，2，…，m;r = 1，2，…，s;j = 1，2，…，n)．

固定成本分摊方案集就是指那些能同时满足决策单元的个体和整体均为有效的固定成本分摊方案的集合，即:

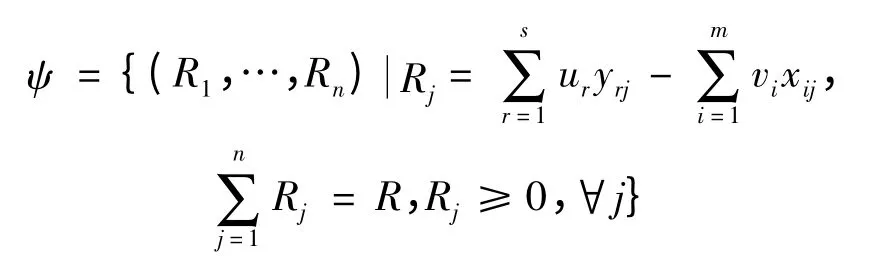
1.2 乘积最大化模型

为了缩小分摊成本额差距，李勇军(2008)引入乘积最大化模型.根据决策单元的个体有效性和整体有效性，建立以下的DEA 模型:Rj为各个DMU 的分摊成本，R 为分摊总成本.

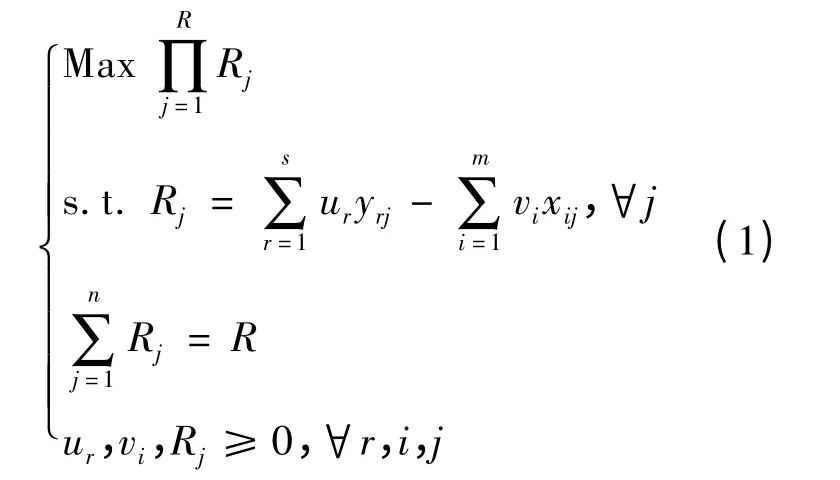
此时，所有的DMU 选择一组共同的权重，该模型可以有效地解决成本分摊差额过大的问题.

2 含公平偏好约束集的乘积最大化模型

DEA 方法虽能综合考虑与固定成本相关联的各要素，但在输入、输出权重系数的选取上往往偏爱优势指标，赋予优势指标过高的权重，忽略了决策者的偏好，同时劣势指标的输入、输出权重系数会出现为0 的现象，而固定成本分摊的各要素缺一不可，因此本节引入带有公平偏好约束集的乘积最大化模型.

文献［5］中Charnes、Cooper、Wei 和Huang等人公开发表的被称为“锥比率”DEA 模型，首次将偏好锥引进到DEA 模型.偏好锥体现的是决策者对输入和输出指标之间的重要性的“偏好”，但所得的“锥比率”太过主观.文献［6］将输入输出指标两两对比形成基于AHP 的判断矩阵反应决策者偏好，但会出现判断矩阵不一致的情形.本节采用专家估计法来获得决策者对各指标的偏好权重，从而构建公平偏好约束集.步骤如下:

步骤1 专家估计法获得指标权重

设输入指标的因素集为Iv= {I1，I2，…，Im}，输出指标的因素集为ou= {o1，o2，…，os}，现有k 个专家各自独立地给出输入、输出指标各因素的权重，如表1所示.

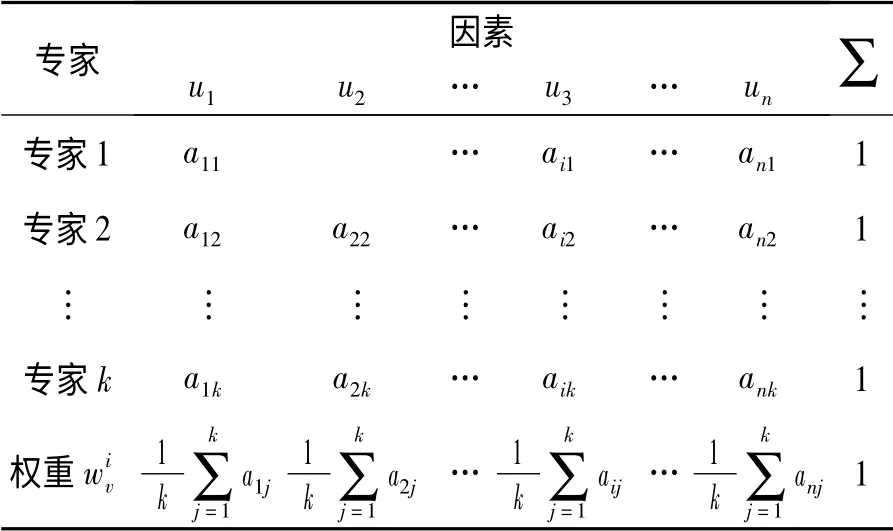
表1 专家权重估计

根据表1，可取各输入指标权重的平均值为各指标权重:

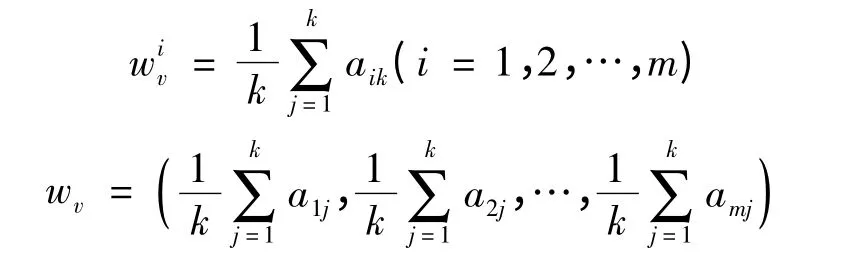
同理可得到各输出因素的权重向量wu.

步骤2 构建公平偏好约束集

令:

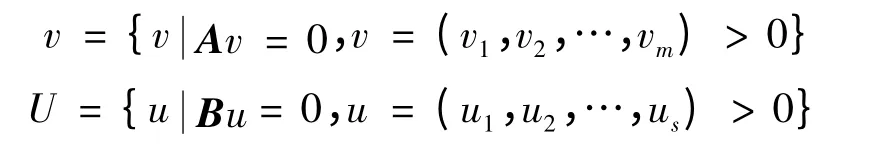
其中:

矩阵A、B 转化为判断矩阵时为一致判断矩阵，其实质就是通过各输入输出指标的偏好权重比值获得决策者的偏好，并称V、U 为公平偏好约束集.

现将公平偏好约束集加入模型中，即可得到含公平偏好约束集的乘积最大化模型.

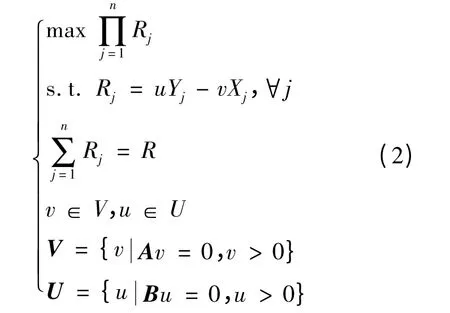
模型(2)中规定v ＞0，u ＞0，以确保所有的指标都能参与固定成本分摊，确保公平性.

3 案例分析

某制造商在安徽省设有17 个地市代理商.2005年，每个市代理商的销售人员数、固定资产值、销售点面积、顾客满意度见表2.当年该制造商在安徽省的广告费用预算总投入为2 500 万元，而实际投入为3 000 万元.制造商要求分摊该预算外费用500 万元.

表2 17 个代理商的指标统计数据

3.1 构建公平偏好约束集

该案例中输入指标因素集Iv= {销售人员数，固定资产，销售点面积}，输出指标因素集Ou={年销售额，顾客满意度}.

步骤1:经过5 位专家估计得wv= {0．39，0．42，0．19}，wu= {0．6，0．4}.

步骤2:由专家估计权重得到公平偏好集为:

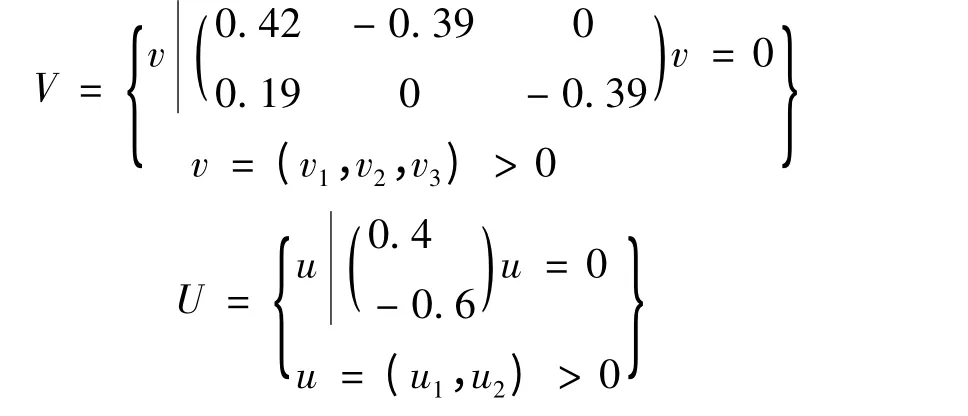
3.2 模型结果

根据带有公平偏好约束集的乘积最大化模型(2)，由Matlab 7.0 计算得到最终的分摊结果如表3所示.现将模型(1)、(2)的分摊结果进行比较.

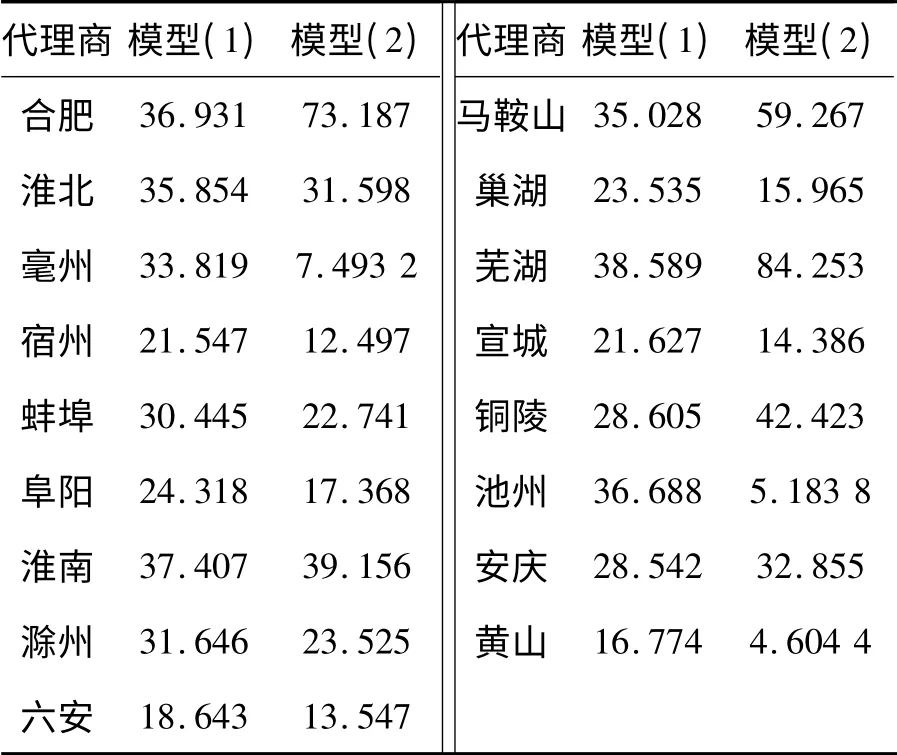
表3 17 个代理商的广告费用分摊方案

由模型(1)得到最优分配方案为:

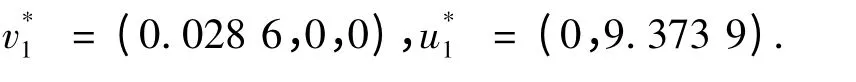
模型(2)的最优分配方案为:

由模型(1)的结果知道，分摊方案只考虑了输入指标v1及输出指标u2，而模型(2)中所有指标的权重均不为0，综合考虑了所有指标，使得分摊方案更具合理性.同时可以看到，同样采用考虑尽量缩小分摊差异的乘积最大化模型，模型(2)的分摊结果与模型(1)的结果有很大的差异.对比合肥与黄山这两个决策单元，黄山的各项投入及产出都比合肥少得多，属于“弱势群体”，而从模型(1)的分摊结果看来，黄山相对于合肥分摊成本差异还是不明显，而模型(2)的结果明显减轻了它的负担.若“弱势群体”分摊的固成本额过高，会加速的它的淘汰，不利于它的发展.因此，考虑决策者偏好的固定成本分摊方案使分摊方案更具可行性.

4 结语

本文在考虑决策者偏好的基础上加入公平偏好约束集，并通过控制各指标权重系数不为0反应分摊的公平性.对于如何控制输入输出权重系数不为0，更多地体现在程序上，本文没有详细描述.本文推广了DEA 方法在固定成本分摊问题中的应用.

［1］Charnes A，Cooper W W，Rhodes E.Measuring the efficiency of decision units［J］.European Journal of Operational Research，1978，2(6):429 -444.

［2］李勇军，梁樑，凌六一.基于DEA 联盟博弈核仁解的固定成本分摊方法研究［J］.中国管理科学，2009，17(1):58 -63.

［3］孙玉华，曾庆铎.基于DEA 的二阶段网络系统的固定成本分摊方法［J］.经济数学，2013，30(1):34-35.

［4］吴育华，曾祥云，宋继旺.带有AHP 约束锥的DEA 模型［J］.系统工程学报，1999，14(4):330 -333.

［5］魏权龄.数据包络分析［M］.北京:科学出版社，2004.

［6］吴华清，梁樑，李勇军，等.救灾管理中的资金配置——基于DEA 的分析［J］.系统管理学报，2011，20(3):348 -349.

［7］王科，李默洁.碳排放配额分配的DEA 建模与应用［J］.北京理工大学学报，2013，15(4):7 -10.

［8］苏翔，葛永达.基于DEA 的造船班组作业责任成本分析［J］.船舶工程，2012，34(2):70 -71.