边界Logistic 违约模型的经验似然统计方法及其应用

侯瑞环，苏佳琳，原星星

(西南交通大学数学学院统计系，四川 成都 610031)

在商业银行信用风险管理中，违约概率是指借款人在未来一定时期内不能按合同要求偿还银行贷款本息或履行相关义务的可能性.早期关于违约概率模型的研究主要以线性判别为主，在线性判别模型中，Beaver 的单变量模型及Altman的多元模型影响最广.在度量企业信用风险时企业是否违约是一个两分类变量，作为两分类因变量的信用状况的概率取值在0 ～1，但在线性模型条件下，不能保证自变量在各种组合下，因变量的取值仍在0 ～1;可通过对因变量作Logist 转换来解决这一问题.就目前而言，建立违约概率模型的有效与主流方法为Logistic 方法.然而Cramer 研究发现，对于贷款违约率的建模用一般的Logistic 模型无法有效解决［1］.换言之，就是一般的Logistic 模型不能够很好解决在H -L 检验中所反映出的Cramer 问题.为了解决这一问题，Cramer 提出了边界Logistic 模型，但并未对边界Logistic 模型优于一般Logistic 模型的原因做理论分析.石小军等［2-4］分析了这种原因，并发现边界Logistic 模型不仅能克服Cramer 问题，而且对临界值不敏感，模型的预测效率也较好.然而，对边界Logistic 模型的参数估计研究较少，主要是运用极大似然估计解决.

经验似然是Owen［5-6］在完全样本下提出的一种非参数统计推断方法，它有类似于bootstrap的抽样特性.这种思想是由 Thomas＆Grun kemeier［7］提出，并在随机删失下发展非参数似然比方法构造生存概率置信区间.Owen将这一思想方法应用到完全独立同分布样本下总体均值的统计推断.然而，相比经典现代统计方法，用经验似然法构造的置信区间有域保持性、变换不变性、Bartlett 纠偏性等突出优点.近年来，一些统计学家又将经验似然方法应用到不完全数据的统计分析，发展了所谓的被估计的经验似然，调整的经验似然及bootstrap 经验似然.在数据分布已知与数据不缺失的情况下，经验似然估计法对参数的估计显得没有参数估计那么高效.实践中数据通常受到不同程度的破坏，这种破坏主要表现在:随机删失、测量误差及数据丢失.Owen在完全样本下的经验似然方法被一些学者基于这3 类被破坏数据进行了统计推断的推广［8-11］.本文在石小军等的研究基础上，进一步讨论边界Logistic 模型的参数估计，并利用经验似然方法给出参数的一种极大经验似然估计，最后通过实证分析，进一步说明这种估计方法得到参数的可靠性.

1 经验似然及模型参数估计

1.1 经验似然

经验似然的方法最早由Owen 提出.这种方法在构造参数置信区域方面有着突出的优点.设X1，X2…，是来自于Rp(p ≥1)的独立同分布随机变量，分布函数为F，在这里无需知道F 的具体参数形式，可以通过一个r 维独立估计函数

对参数θ 进行估计，并由Qin＆Lawless 给出了如下估计方程［12］:

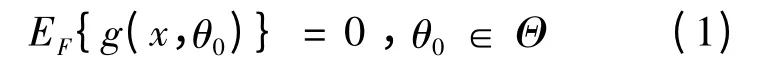
EF与θ0表示关于分布F 的数学期望和参数θ 的真实值，通常也将上述估计方程称为矩条件方程.

Owen 给出经验似然方程，定义为

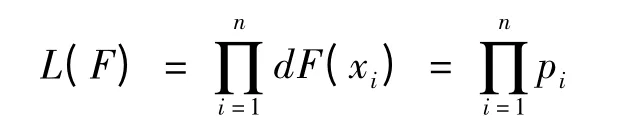
其中pi= pr(X = xi).在条件(1)下经验似然比函数为

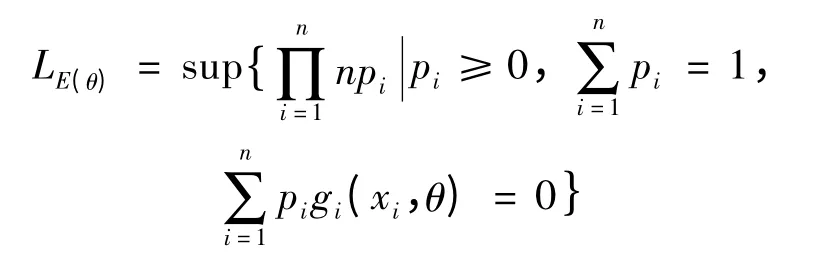
同时Owen 与Qin＆Lawless 指出，当

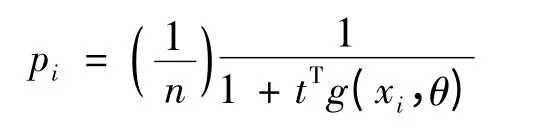
时，上述经验似然比函数LE(θ)有唯一值:

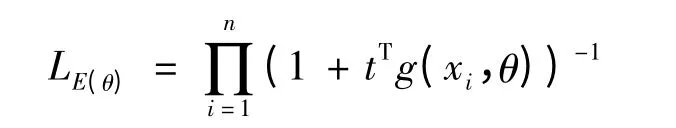
其中t 与θ 和n 有关，并且可通过方程

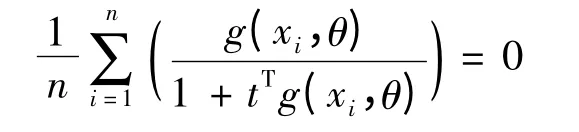
确定t.

1.2 边界Logistic 模型的极大经验似然估计

Cramer 给出边界Logistic 模型为:

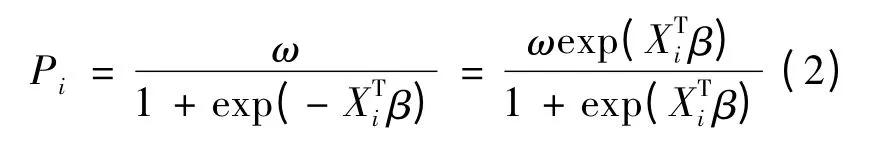
其中ω 为［0，1］之间的任意常数，称为违约边界.Xi是第i 个自变量值，β 为一个包含截距项的系数向量，对于模型(2):

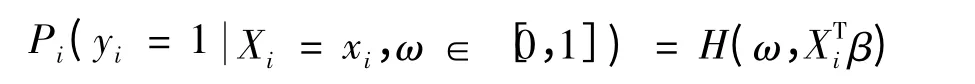
其中设Z = XTiβ，则

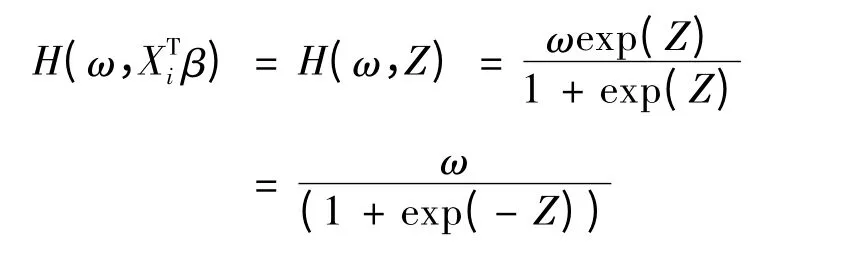
参数β 的参数似然为:

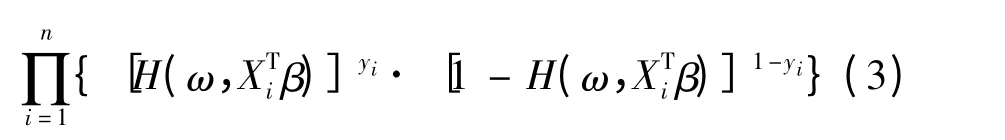
对数似然为:

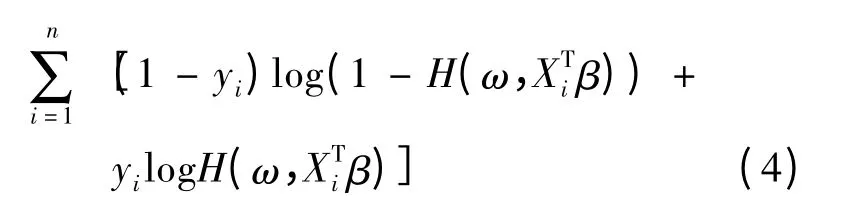
对上式求关于β 的导数得到估计方程为:

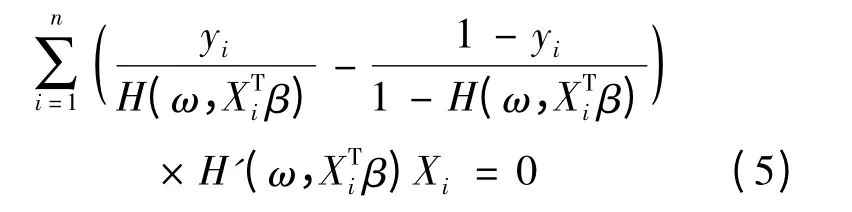
在这里

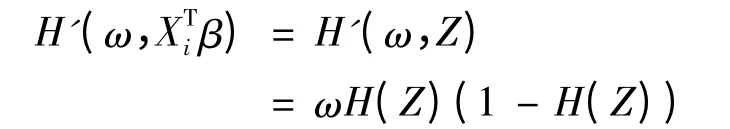
由此(5)式估计方程可简化为

ω ∈［0，1］为任意常数，故而(6)式也可表示为

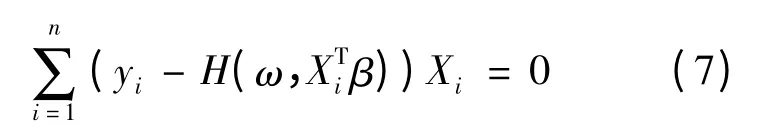
因此，边界Logistic 模型的经验似然比函数为:

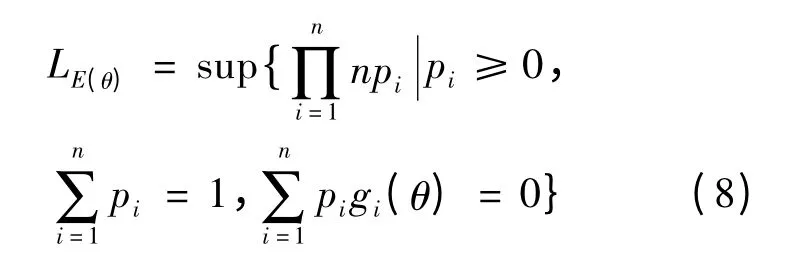
这里估计函数

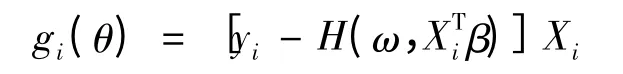
可根据(7)式得到参数β 与ω 的极大经验似然估计方法，即参数θ 的经验对数似然函数为:

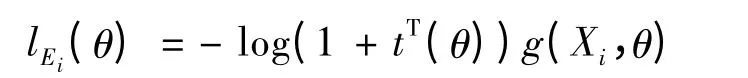
其中θ = (ω，βT)T∈Θ 的参数向量，

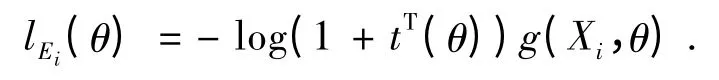
假设t 与θ 相互独立，类似于丁先文等［13］对Logistic模型基于检验似然估计的方法，可定义:

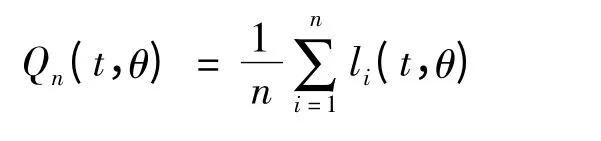
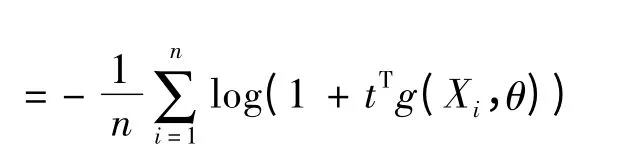
t 与上文一样，都与n 和θ = (ω，βT)T∈Θ 有关.

显然，参数θ = (ω，βT)T∈Θ 极大经验似然估计和t 的估计为下列方程组

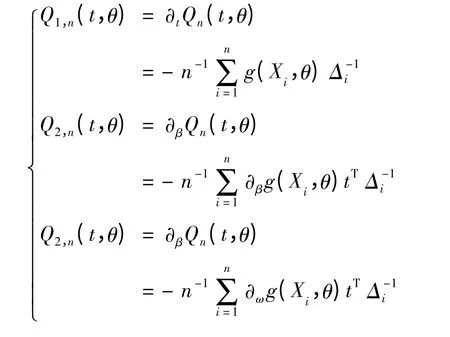
的解，其中

由此可以得到边界Logistic 模型参数β 与ω 的极大经验似然估计^β 和^ω.

2 实证分析

2.1 样本与指标

本文选用2012年第一至第四季度40 家房地产行业上市公司的主要财务数据进行研究.其中有20 家公司的每股收益大于零，认为其为正常运行公司，定义其信用度为1.另外20 家公司每股收益小于零，为违约公司，定义其信用度为0.模型样本包括了这一年的总资产利润率、流动比率、存货周转率等12 个指标(见表1)，并且采用参数两独立样本T 检验和非参数的K -W 检验对指标变量进行分析，分析结果见表2与表3.由于指标之间存在线性或非线性关系，通过因子分析方法消除多重共线性，分析结果见表4.由因子分析的总方差解释表可知，变量相关矩阵的前3 个因子的特征值大于1，它们一起解释了总方差的87.81﹪.最终选出3 个因子来研究房地产上市公司的信用风险.

表1 银行对房地产客户信用评级五大指标

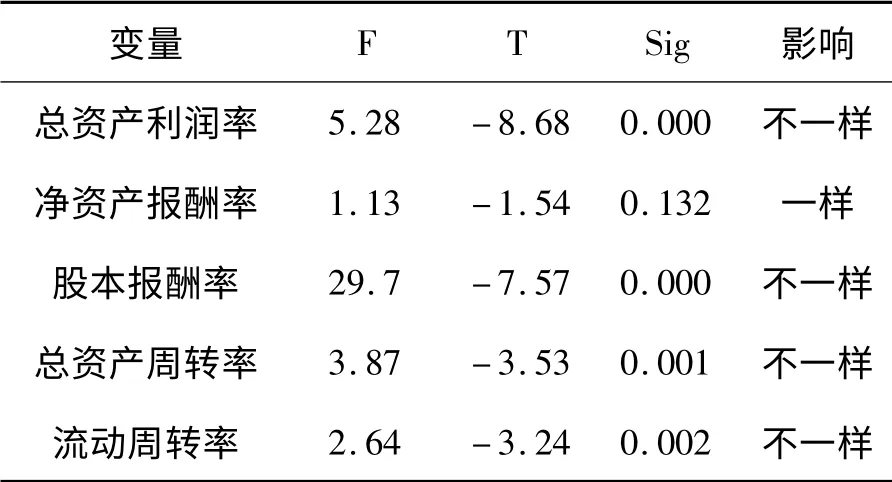
表2 两独立样本T-检验结果

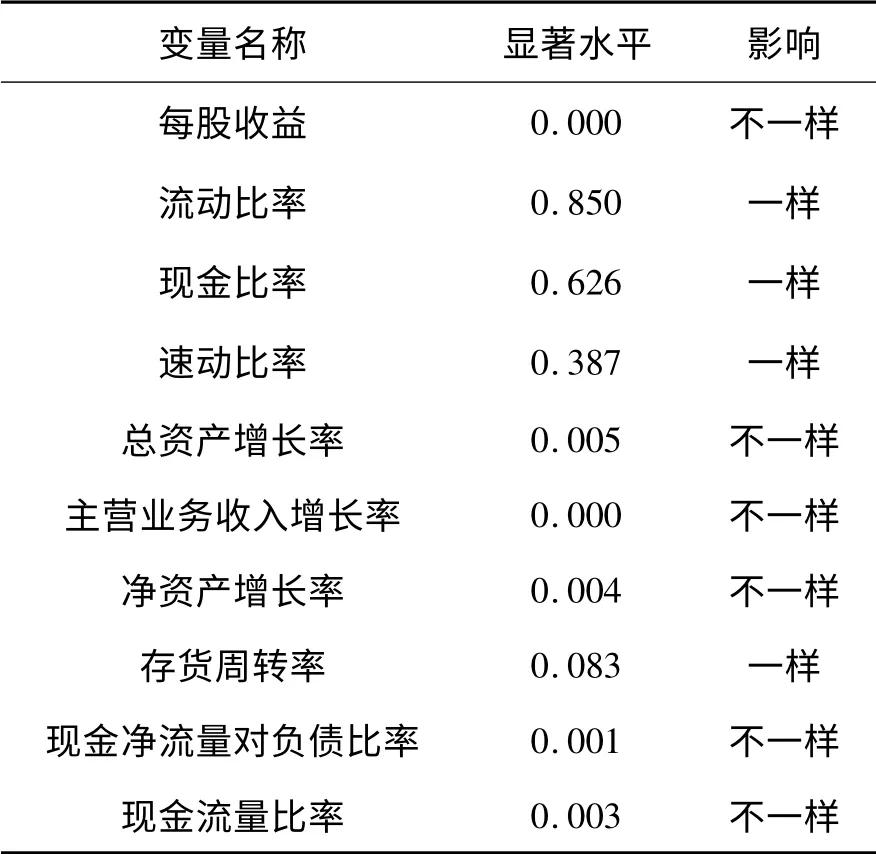
表3 两独立样本K-W 检验结果

通过T 检验和K-W 检验的结果可知，所有指标中显著的指标有每股收益、总资产利润率、股本报酬率、总资产增长率、主营业务增长率、净资产增长率、总资产周转率、流动资产周转率、经营现金流对负债比率以及现金流量比率.这也表明上市公司在这几个指标正常时就可以避免或很少出现违约现象.

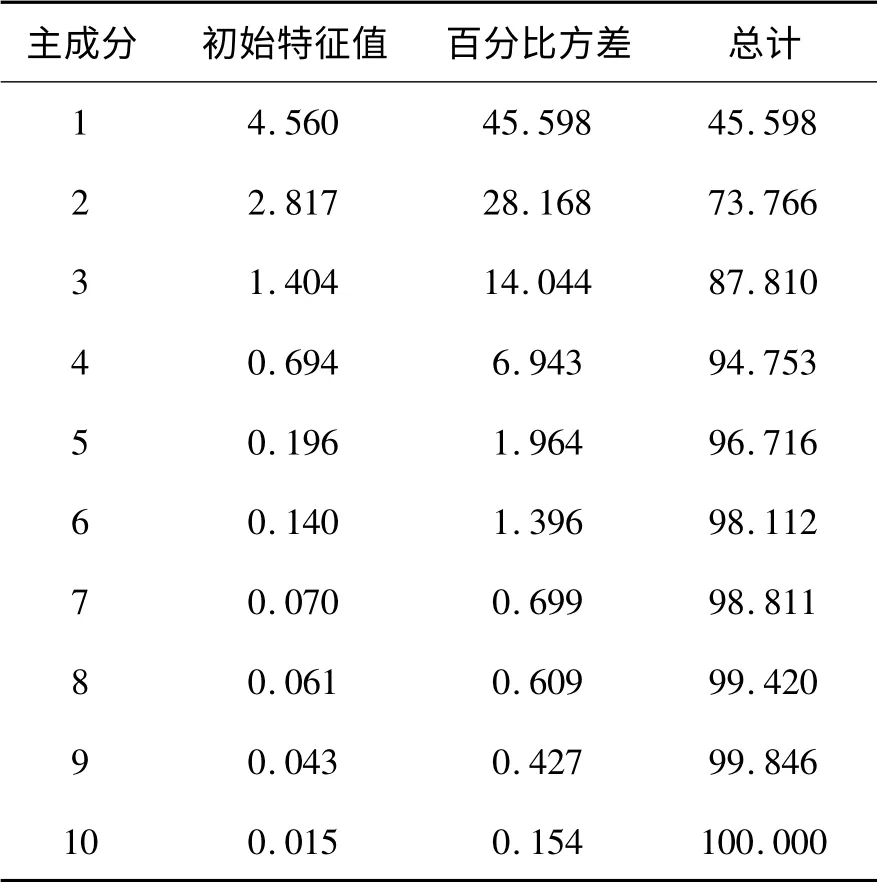
表4 因子分析结果

2.2 估计结果

利用R 软件求解出边界Logistic 的极大经验似然非线性方程组，得到各参数的估计结果，见表5.

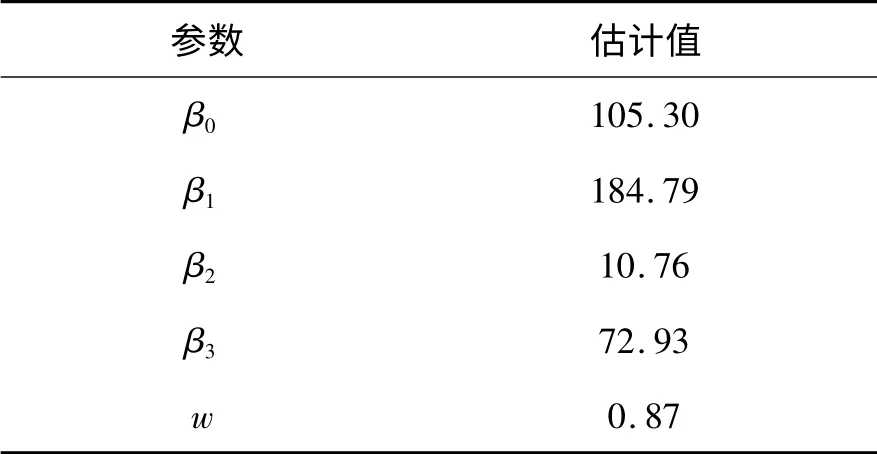
表5 边界Logistic 模型系数估计结果

因此，边界Logistic 违约率模型为:

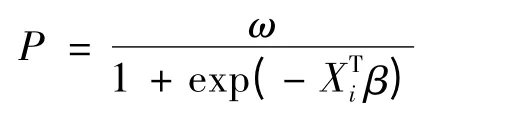
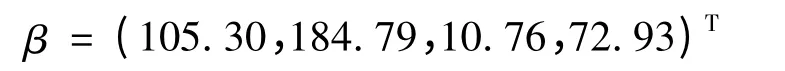
有x1，x2，x33 个指标最终进入模型.由此看出企业的净利润、盈利能力、营运能力以及成长能力对房地产行业信用风险的影响较大，其中影响最大的是企业的成长能力.也就是说，在房地产行业里，成长能力强的企业会有很大的获利空间，从而也较大幅度地降低对投资者产生违约的危险.

再利用这个边界Logistic 违约模型计算出样本的违约率，并得到违约率分布，如图1.

图1 边界Logistic 违约模型的检验样本违约率分布图

3 结果分析与讨论

(1)边界Logistic 违约模型计算出的违约率剔除了灰色区域，能够很好观测出上市公司违约与否.

(2)边界Logistic 违约模型的系数估计除了极大似然估计方法，也可以利用经验极大似然估计求解，二者的估计结果差不多，但经验极大似然法对数据的分布不做任何要求.

(3)除了Cramer 问题，同样可以研究其对临界点的稳定性，也可以在文章找到边界Logistic违约模型对临界点更稳定的依据(见图1).

(4)本文仅仅利用经验极大似然估计方法研究了边界Logistic 违约率模型的参数估计，同样也可以立足于经验似然对估计参数尝试给出区间估计.

［1］Cramer J S.Scoring banking loans that may go wrong -a case study［J］.Statistic Neerlandica，2004，58(3):365 -381.

［2］石晓军，肖远文，任若恩.边界Logistic 违约率模型Bayes 分析及实证研究［J］.中国管理科学，2006，(14):25 -29.

［3］石晓军，肖远文，任若恩.Logistic 违约率模型的最优样本配比与分界点研究［J］.财经研究，2005(9):39-49.

［4］Shi X J.Robust factor credit discriminate model and empirical evidences from China［A］.proceedings of the 7th International Conference on industrial Management.China Aviation Industry Press，2004:491 -497.

［5］Owen A B.Empirical likelihood ratio confidence intervals for a single function［J］.Biometrika，1988，75(2):237 -249.

［6］Owen A.Empirical likelihood for linear models［J］.Ann Statistic，1991(19):1725 -1747.

［7］Thomas D R，Grunkemeier G L.Confidence interval estimation of survival probabilities for censored data［J］.Amer Statistic Assoe，1975(70):865 -871.

［8］Wang Q H，Jing B Y.Empirical likelihood for a class of functions of survival distribution with censored data［J］.Ann Inst Statistic Math，2001(53):517 -527.

［9］Wang Q H，Wang J L.Inference for the mean difference in the two - sample random Censorship model ［J］.Journal of Multivariate Analysis，2001(79):295 -315.

［10］Li G，Wang Q H.Empirical likelihood confidence regre ssion analysis with right censored data［J］.Statistic Siniea，2003，13(1):51 -68.

［11］Wang Q H，Rao J N K.Empirical likelihood for linear regression models under imputation for missing response［J］.Canadian Journal of Statistics，2001，29(4):597 -605.

［12］Qin J，Lawless J.Empirical likelihood and general estimating equations［J］.Ann Statistic，1994(22):300 -325.

［13］丁先文，陈绚青，周友明，等.Logistic 回归模型的经验似然诊断［J］.数学的实践与认识，2013(43):140-148.