谈谈基元反应速率的过渡状态理论*

刘国杰 黑恩成

(华东理工大学化学系 上海200237)

1935年，Eyring和Polanyi在简单碰撞理论的基础上，将量子力学和统计力学应用于化学反应速率的研究中，建立了基元反应的过渡状态理论，从而使反应速率的研究迈上了一个新的台阶。虽然由于种种困难，目前人们还不能准确地预测反应速率，但这个理论为现代化学反应动力学的发展提供了重要的基本概念和理论基础，本文拟从不同的视角分析这个理论，试图加深对它的理解。

1 微观化学反应向宏观化学反应的过渡

对于宏观基元反应

从微观的角度考虑，也可表示为［1］:

式中i，j和m，n分别表示反应物A，B和产物C，D所处的量子态，意即这些反应物和产物都包括了各种可及的微观状态。因此，一个宏观的基元反应包含了各种微观的态与态之间的基元反应。这些态-态反应是在微观层次上进行的。近代，由于交叉分子束和激光脉冲等实验技术的发展，态-态反应的研究已变得可能。这样，化学反应的研究便分成了如下3个层次［2］:

①微观的基元化学物理反应研究，即上述态-态反应。由于这部分研究完全涉及微观的性质，理论上应该用量子力学来处理。

②宏观化学反应研究。它是从宏观的基元反应出发，来推求总包反应的动力学。换句话说，就是要确立化学反应的机理，即化学反应是由哪些宏观的基元反应所组成。这部分探讨是唯象的，属于化学反应动力学的经典理论。

③以微观的基元化学物理反应出发，建立宏观的基元反应动力学理论。它介于①与②之间，是微观向宏观反应动力学的过渡，在这一层次的理论研究中，统计力学起着不可或缺的作用。

本文要涉及的过渡状态理论属于第③个研究层次。

2 活化络合物不能用宏观方法测定

应该指出，对于任何反应，首先必须活化反应物，然后才能反应。基元反应亦不例外，除非反应物本来就处在活化状态，例如自由基反应等。因此，式(2)可表示为:

需要指出的是，这种活化络合物并非化合物。量子力学的计算表明，当反应物分子A与B相互接近时，由于电子云的排斥作用，它们的作用势能会因此而升高。当两个反应物分子开始发生化学作用，即新键开始形成和旧键将要断裂时，势能达到极大值，此时的反应系统即处于过渡状态。此后便因变成了产物C和D，势能逐渐降低。这种处于过渡状态时的反应系统即为活化络合物≠。由于活化络合物并不是化合物，它的存在是不能用宏观方法测定的，这就是说，式(3)与式(2)一样，是个一步完成的基元反应。图1是这个基元反应的势能曲线，它得自量子力学算得的势能面。

图1 基元反应的势能曲线

Eyring假设基元反应就是按照式(3)所示的模式进行，并认为反应物与活化络合物可视为始终处于热力学平衡中。即:

且认为，活化络合物一经分解成产物便不再复返。因此，基元反应的速率常数当为:

由此可见，活化络合物构型的确定和分解频率的计算是过渡状态理论的关键。前者带有一定的推测和随意性，而后者则不能不借助于活化络合物的微观模型。

3 活化络合物的微观模型

这里介绍两个常用的微观模型［3］。

3.1 活化络合物的振子模型

这个模型将活化络合物沿着反应坐标的不对称伸缩振动视为频率很低的单维简谐振动，认为正是这个振动的频率决定了活化络合物的分解频率，因为它的每一次振动都会引起活化络合物的分解。这就是说，这个模型是将活化络合物≠视为一个单维简谐振子。

量子力学表明，当能量标度的零点设在基态能级上时，处在l量子态的简谐振子的能量为:

式中vl为处在l量子态的振子的振动量子数，故活化络合物的总能量当为:

式中Nl为处在l量子态的振子数。所以，

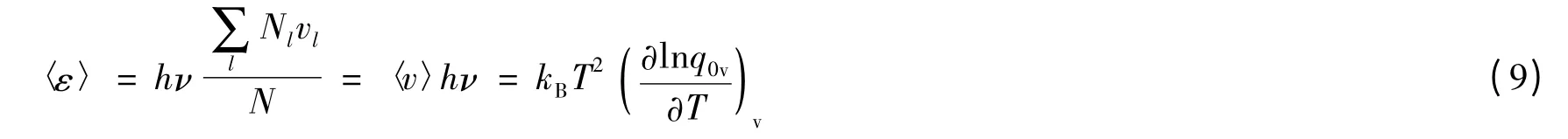
式中〈v〉为振子的平均振动量子数，后面将要看到，它的出现在本工作中起着重要的作用。

由于振子的振动频率很低，其配分函数

将式(10)代入式(9)，经运算后可得:

于是，由式(6)不难得到:

3.2 活化络合物的平动子模型

在图1的势能曲线能峰上，有一段长度为δ的狭窄的水平区域。在这一区域中，反应系统的势能基本保持不变。Eyring认为，处在这个区域中的反应系统都是活化络合物，只有当系统越出这个区域时，活化络合物才分解成产物。因此，在这个区域中，振动蜕变成有效质量为m≠的平动子在一维箱中的平动运动。活化络合物分解成产物的频率当为:

所以，

式(16)亦即Eyring方程。

4 一个有实用价值的推论

Eyring方程理应具有预测化学反应速率的功能，因为它的计算只需要光谱和势能面提供的数据，故理论建立之初，人们对它抱有很大的期望，但是不久便有些失望，原因是势能面的计算准确性还达不到定量预测的要求。此外，如上面已经提及，活化络合物构型的确定也还带有一定的推测和随意性，这便影响了光谱数据的准确选择。故目前这个理论还只能用来定性地解释许多实验事实。与其这样，还不如改变Eyring方程的形式，使它能用来关联各种实验得到的动力学数据。

如上所述，活化络合物≠可视为一个振动频率很低的单维简谐振子。式(11)表明，其平均振动量子数〈v〉必定是个很大的值，且当振动频率指定，亦即振子的能级间隔一定时，〈v〉的大小应仅是温度的函数。故随着温度升高，因振子会向高能级扩散，〈v〉值必定迅速随之增大。因此，有理由推测〈v〉与T应呈幂函数关系，即:

式中α是一个常数，且α＞1。故式(11)可表示为:

式中β=kB/h，n=1-α是一个负数。

将式(19)积分，不难得到:

式中A是积分常数。代入式(18)，即得:

式中B=Aβ，它与n、E是方程(21)的3个参数。它们都有明确的物理意义，文献［5］已作了详细的交待。式(21)便是本文所得推论，亦称修正的Arrhenius方程。在物理化学教材中，很少有不提及这个方程的，它能够满意地关联宽阔温度范围内实验得到的动力学数据，且关联得到的E才是该反应名副其实的活化能。

最后应该指出，过渡状态理论是有某些局限的。其中一个最主要的局限是，它只能应用于分解频率很低的活化络合物，即hν≪kBT的情况。倘若在活化络合物构型中，沿着反应坐标的不对称伸缩振动的频率较高，以致hν≥kBT，传统的过渡状态理论就不再适用。此时，为使活化络合物分解成产物，系统必须补充能量。为此，文献［6］建立了一个扩展的过渡状态理论，它能适用于各种大小的分解频率。据此得到的n值便不再拘泥于负值。

［1］俞书勤.微观化学反应.合肥:安徽科学技术出版社，1985

［2］赵学庄.化学反应动力学原理(上册).北京:高等教育出版社，1984

［3］Nicholas J.化学动力学——气体反应的近代综述.吴树森译.北京:高等教育出版社，1987

［4］Moore J W，Pearson R G.化学动力学和历程——均相化学反应的研究.第3版.孙承谔译.北京:科学出版社，1987

［5］刘国杰，黑恩成.大学化学，2013，28(6):46

［6］刘国杰，黑恩成.大学化学，2014，29(3):72