一类具阻尼项的六阶非线性波动方程的Cauchy问题

宋瑞丽, 郭红霞

(1.中原工学院 信息商务学院 河南 郑州 450007； 2.郑州大学 数学系 河南 郑州 450001)



一类具阻尼项的六阶非线性波动方程的Cauchy问题

宋瑞丽1, 郭红霞2

(1.中原工学院 信息商务学院 河南 郑州 450007； 2.郑州大学 数学系 河南 郑州 450001)

研究了一类具阻尼项的六阶非线性波动方程的Cauchy问题，利用压缩映像原理和积分估计，在小初值的条件下，得到解的整体存在性、唯一性和衰减性.

非线性波动方程； Cauchy问题； 整体解； 压缩映射原理

0 引言

研究具阻尼项的六阶非线性波动方程的Cauchy问题

utt-uxx+uxxxxtt+uxxxx+ut-uxxt=f(u)xx,x∈Rn,t>0,

(1)

u(x,0)=u0(x)；ut(x,0)=u1(x),x∈Rn

(2)

ScottRussell对孤立水波的探讨推进了人们对描述流体中波动现象的非线性偏微分方程的研究[1].Wang等[2]研究了多维IMBq方程

utt-Δu-Δutt=Δf(u)

(3)

Cauchy问题解的存在性.Cho等[3-4]利用Besov空间改进了文献[2]中的一些结果.Ploat[5]研究了具阻尼项的IMBq方程

utt-Δu-Δutt-Δut=Δf(u)

(4)

1 线性方程的衰减估计

本节讨论线性Cauchy问题

utt-uxx+uxxxxtt+uxxxx+ut-uxxt=gxx,x∈Rn,t>0,

(5)

u(0)=u0(x)；ut(0)=u1(x)

(6)

解的衰减性质.利用Fourier变换和Duhamel原理,式(5),(6)的解可表示为

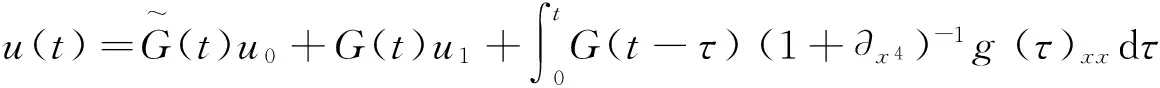
其中，

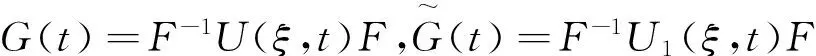
(7)

(8)

(9)

(10)

(11)

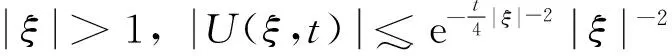
(12)

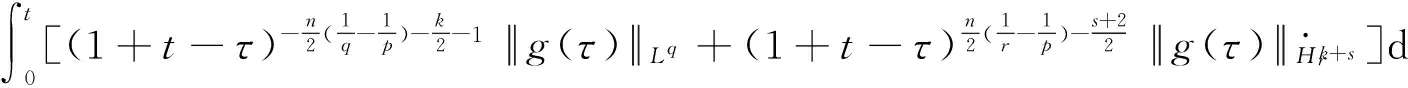
(13)

利用Duhamel原理和引理1、引理2可得到定理1.

(14)

其中，γ≥0.

2 整体解的存在性和衰减性

本节将利用压缩映像原理和积分估计式在上节的基础上，讨论Cauchy问题(1),(2)解的存在性及衰减性.

(15)

(16)

其中，ρ是只依赖于f和δ的小的正常数.

(17)

下面证明N是从X到X的严格压缩映射.在定理1中取k=0,p=∞,r=2，注意到α≥2，利用文[6]中的引理3.1，3.2和式(15)，得

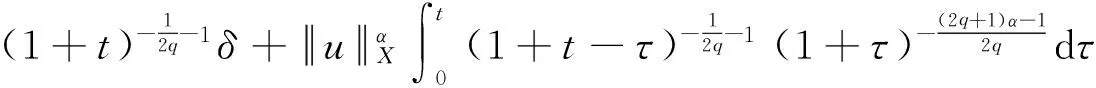
(18)

(19)

(20)

类似式(18)～(20)的证明方法，有

因此，对于充分小的ρ,N是(X,d)上的压缩映射.利用压缩映像原理,N(u)在X上存在唯一的不动点u(x,t),它是Cauchy问题(1)，(2)的解,且满足式(16).

[1] Russell J S. Report on waves [C]//Report of 14th Meeting of the Association for the Advancement of Science.New York,1844:311-390.

[2] Wang Shubin, Chen Guowang. Small amplitude solutions of the generahzed IMBq equation[J]. Math Anal Appl, 2002, 274(2)：846-866.

[3] Cho Y, Ozawa T. Remarks on modified improved Boussinesq equations in one space dimension[J].Proc R Soc A,2006,462(5):1949-1963.

[4] Cho Y, Ozawa T. On small amplitude solutions to the generalized Boussinesq equations[J]. Discrete and Continuous Dynamical Systems, 2007,17(4)：691-711.

[5] Necat P．Existence and blow up of solutions of the Cauchy problem of the generalized damped multidimensional improved modified Boussinesq equation[J]. Z Naturforsch,2008(63a):543-552.

[6] Wang Shubin, Xu Huiyang. On the asymptotic behavior of solution for the generalized IBq equation with hydrodynamical damped tern[J]. J Differ Equations, 2012,252(7):4243-4258.

[7] 李向正，郝祥晖.简化齐次平衡原则与Gerdjikov-Ivanov方程的精确解[J].河南科技大学学报：自然科学版，2015，36(1)：82-85.

Cauchy Problem for a Class of Damped Six Order Nonlinear Wave Equation

SONG Rui-li1， GUO Hong-xia2

(1.CollegeofInformation&Business,ZhongyuanUniversityofTechnology,Zhengzhou450000,China;2.ZhengzhouUniversity,Zhengzhou450001，China)

The Cauchy problem of a class of damped six order nonlinear wave equation was studied. For sufficiently small initial data, the existence, the uniqueness and the asymptotic behavior of solution were proved by the contraction mapping principle and integral estimates.

nonlinear wave equation; Cauchy problem; global solution; contraction principle

2014-11-04

国家自然科学基金资助项目，编号11171311；河南省自然科学基金资助项目，编号132300410351，河南省科技厅重点攻关项目，编号132102210185.

宋瑞丽(1978-)，女，河南新野人，讲师，硕士，主要从事偏微分方程研究，E-mail：srli070911@sina.com.

O175.29; O29

A

1671-6841(2015)01-0010-04

10.3969/j.issn.1671-6841.2015.01.003