钢结构半刚性连接弯矩-转角关系模型研究

杨卫忠, 王 茜

(郑州大学 土木工程学院 河南 郑州 450001)



钢结构半刚性连接弯矩-转角关系模型研究

杨卫忠, 王 茜

(郑州大学 土木工程学院 河南 郑州 450001)

承受弯矩作用的钢结构半刚性节点可离散为两端通过刚性体连接的细观单元并联体，而细观单元体则假定为理想弹脆性体，定义单元体失效数目与总数目之比为损伤变量，根据平衡条件和损伤力学理论，导出了半刚性节点单调受弯时的损伤本构关系模型，分析得出的弯矩-转角关系式仅与节点的初始刚度、极限弯矩及相应的转角有关，该式能反映半刚性节点本构关系的非线性特征，而且与已有试验结果吻合良好.

钢结构； 弯矩-转角关系； 损伤； 半刚性连接

0 引言

钢框架在结构分析时，梁柱的连接通常假定为刚接或铰接，刚接时需将梁的翼缘与柱焊接，同时将梁的腹板与柱翼缘焊接，或通过螺栓与柱翼缘上的节点板连接，而铰接则仅需将梁的腹板通过螺栓和柱相连接.前者构造复杂且梁跨中截面不能充分利用，后者尽管构造简便，但仅利用了梁跨中截面且结构的变形较大.采用梁柱的半刚性连接则能避免其不足，梁柱端板连接就是典型的半刚性连接，但是，半刚性连接的结构分析则需要其弯矩-转角关系，而我国现行的《钢结构设计规范》[1]则无具体的表达式.由此吸引了众多研究者对半刚性连接研究的关注，仅半刚性连接节点的弯矩-转角关系就有多种表达式[2-7]，既有单一形式的线性型、多项式型、幂函数型和指数型，也有线性和函数的组合型.

考察上述本构关系后不难看出，线性型的优点是形式简单、计算方便，但计算的精度不高是其缺点，而折线型虽能提高精度，但又存在刚度突变的不足；多项式型虽然在一定范围内能够较好地反映半刚性连接的弯矩-转角关系，但是由于多项式本身的特性会使得曲线在某一范围内会出现拐点，且该表达式中参数也无明确的物理意义；幂函数型则需引入形状系数来反映不同连接类型.更为突出的是，已有本构关系模型的共性是没有理论基础.

本文认为，合理的本构关系模型应该具有下列特点：首先要具有理论基础；其次是能解释其受力特性；最后，模型中的参数要少且易于确定，其预测结果也要经得起检验.基于此观点，本文就通过一个细观损伤物理模型来解释承受弯矩作用的半刚性连接节点弯矩-转角曲线非线性的原因，基于损伤力学原理和细观损伤模型的平衡条件，直接导出了半刚性连接节点的弯矩-转角关系模型的一般式，而损伤演化则由模型中的细观单元体破坏强度分布特点来确定.最后，利用曲线的特征点条件来确定模型参数，从而得到具体的表达式.

1 半刚性连接损伤机制和基本假定

将钢结构半刚性梁柱节点的连接部分离散为若干个具有一定特征长度和截面面积的细观单元，为了便于推导本构关系模型，将梁柱视为刚性体，这样，每一个细观单元就具有了相同的转角.这里，细观单元用弯曲微弹簧来表示.细观单元的破坏是由于微弹簧的转动超过了其极限转角而引起的，节点的细观损伤模型如图1所示.该细观损伤模型能够较好地解释半刚性连接节点的宏观受力特性[8].

推导半刚性节点本构关系模型的基本假定有：① 每个细观单元的弯矩相同，且其弯矩-转角关系为理想弹脆性关系，如图2所示；② 细观单元的极限转角组成一个均匀随机场.

图1 节点受弯细观模型

图2 微弹簧的弯矩-转角关系

2 损伤变量

图1模型中的损伤变量D采用经典损伤力学的定义，即

(1)

式中，n，N分别为节点中发生破坏的单元数和总单元数.

在外弯矩M作用下，节点产生宏观转角θ，而因细观单元损伤而产生的失效单元数目为

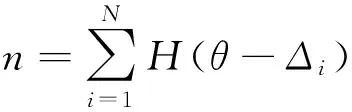
(2)

这里，H(·)是 Heaviside函数，即

(3)

当N趋于无穷大时，等效单元体可视为一维连续体，进一步将单元体破坏时的转角假定为连续随机场Δ(x)，不失一般性地假定x∈[0,1]，由式(1)～(2)得

(4)

式中，Δ(x)表示位置x处的随机破坏转角.

对于有限细观单元体的集合，其破坏弯矩分布一般属于Weibull 分布，而对于无限集合体，则趋于正态分布.这里，假定细观单元的破坏弯矩为对数正态分布，即全部细观单元破坏转角组成一个均匀随机场，其均值和标准差分别为λ,ζ.因此，在转角θ时的损伤为

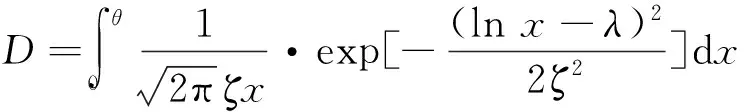
(5)

显然，式(5)的损伤函数满足一般损伤变量的全部特征.

3 节点的弯矩-转角关系

3.1 本构关系模型

在外部弯矩M作用下，节点产生宏观转角θ，宏观外弯矩即等于未破坏单元弯矩之和，根据前面的细观模型和损伤的定义，节点的弯矩与转角关系为

M=K0θ(1-D),

(6)

式中，K0为节点的初始转动刚度.

式(6)即为半刚性节点受弯时的损伤本构关系模型.可以看出，由于损伤发展，引起节点转动刚度降低.确定损伤变量中的参数λ,ζ后，将式(5)代入式(6)，即得到具体的弯矩-转角关系式.此外，若式(6)中的损伤变量取某特定表达式，该式就变为Chen-Kishi模型.

3.2 参数研究

(7)

从式(7)中可明显看出：弯矩-转角曲线仅与节点的初始转动刚度、极限弯矩及转角有关，其中，初始转动刚度与峰值割线转动刚度的比值是主要影响因素.确定Mu,K0和θu这3个参数即可得到半刚性连接具体的弯矩-转角关系.

针对不同的半刚性连接形式，研究者们提出了多种Mu和K0的计算方法.这里，采用目前发展较为成熟的欧洲规范EUROCODE3[6](以下简称EC3)来计算半刚性节点的抗弯承载力Mu和初始转动刚度K0，而另外，根据施刚[9]的研究，可确定极限弯矩对应的转角.

4 试验验证

为了验证上述分析方法的合理性，以高强螺栓平齐端板连接节点为研究对象，将本文方法的理论预测结果[10-11]与部分试件的试验结果和有限元分析结果[8]进行比较，节点参数分别示于图3和表1中,其中，e=33mm，p=65mm，螺栓为10.9级的M22.而部分试件的理论预测结果与试验结果和有限元分析结果的比较如图4、5所示.

图3 节点中参数定义

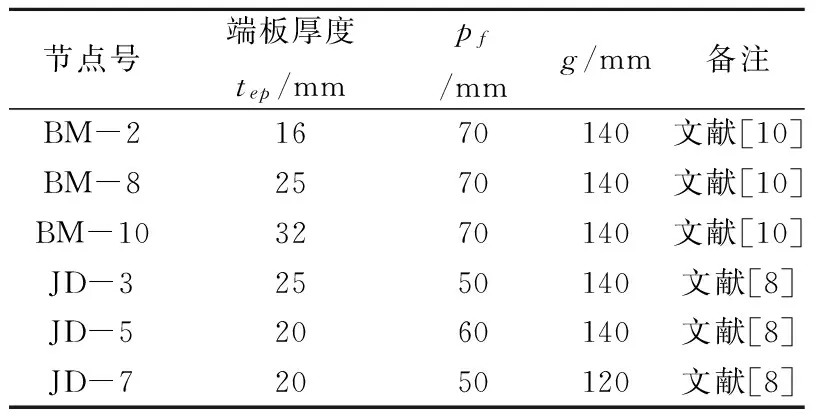
表1 试件参数Tab.1 Coefficients in the specimen

从图4、5不难看出，本文方法的计算结果与试验结果和有限元结果均吻合良好.在加载初期，由于材料处于弹性阶段，理论曲线与试验或有限元分析曲线基本重合，进入非线性阶段后，理论预测曲线与试验结果虽有偏差，但总体趋势保持一致.由此说明本文分析方法是可行的，而且合理.

图4 理论曲线与试验结果的比较

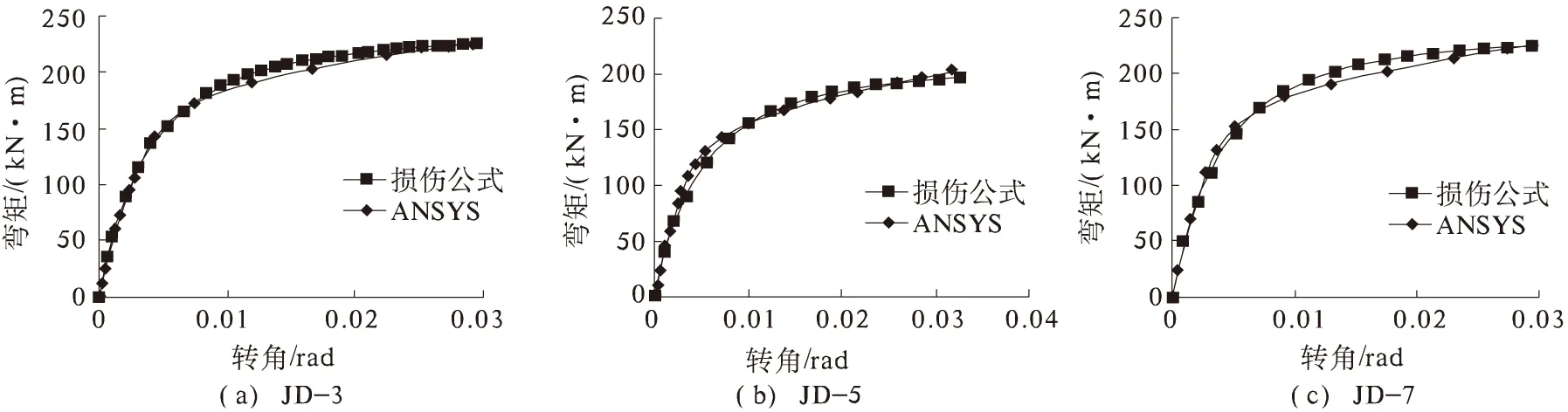
图5 理论曲线与有限元结果的比较

5 结语

基于细观模型和损伤力学原理，可导出钢框架半刚性节点在单调弯矩作用下的弯矩-转角关系模型，通过参数研究得到的本构关系表达式不仅有理论依据，而且具有适用性好、参数少而易于确定等优点，并能反映节点受弯过程中的刚度退化.与已有本构关系模型不同的是，本文建立的半刚性节点本构关系模型不仅有上升段，而且还有下降段.初步的验证说明了该方法的合理性，可作为进行钢结构半刚性连接结构分析的弯矩-转角关系.

[1] 中华人民共和国建设部．钢结构设计规范[S]．北京：中国计划出版社，2003.

[2] 李国强，石文龙，王静峰．半刚性连接钢框架结构设计[M]．北京：中国建筑工业出版社，2009.

[3] Frye M J，Morris G A．Analysis of flexibly connected steel frames[J]．Canadian Journal of Civil Engineering, 1975，2(3)：280-291.

[4] Chen W F，Kishi N．Moment-rotation relations of semi-rigid connections with angles[J]．Jounral of Sturcutral Engineering，ASCE，1990，116(7)：1813-1834.

[5] Yee Y L，Melchens R E．Moment-rotation curves for bolted connections[J]．Jounral of Structural Engineering，1986，112(3)：615-635.

[6] European Committee for Standardization (CEN) . Eurocode3，Design of steel Stuuctures，Part l．8：Design of joints[S].PrEN1993-1-8，2003.

[7] 谭德坤.量子粒子群算法优化钢结构截面[J].河南科技大学学报：自然科学版，2011，32(3)：47-51.

[8] 王茜．钢框架梁柱平齐端板连接的损伤本构关系研究[D]．郑州：郑州大学，2012.

[9] 施刚．钢框架半刚性端板连接的静力和抗震性能研究[D]．北京：清华大学，2004.

[10]吴保国．钢框架梁柱节点高强度螺栓端板连接的试验研究[D]．郑州：郑州工学院，1992.

[11]杨卫忠，王茜.钢框架梁柱节点平齐式端板连接的数值分析[J].四川建筑科学研究，2013，39(4)：39-42.

Constitutive Equation Model for Semi-rigid Connection of Steel Structure

YANG Wei-zhong， WANG Qian

(SchoolofCivilEngineering,ZhengzhouUniversity，Zhengzhou450001，China)

The semi-rigid connection joint in steel frame could be characterized by a meso-damage model which was composed of a set of brittle linear-elastic flexural springs of equal stiffness joined in parallel. And the nonlinear performance of the moment-rotation curve of the joint was analyzed. Based on the equilibrium equation and damage theory, a damage constitutive model of steel frame joint subjected to monotonic moment was deduced. The coefficients used in the model could be determined by initial flexural stiffness and ultimate moment. It was found that theoretical curve had a good agreement with experiments.

steel structure; moment-rotation relationship; damage; semi-rigid connection

2014-08-04

河南省科技攻关重点项目，编号132102210500.

杨卫忠(1966-)，男，江苏苏州人，教授，博士，主要从事土木工程结构分析理论与应用研究，E-mail:ywz6518@hotmail.com.

TM153+.1

A

1671-6841(2015)01-0115-04

10.3969/j.issn.1671-6841.2015.01.025