谈物理解题思维起点

◎福建省漳浦达志中学 陈满和

谈物理解题思维起点

◎福建省漳浦达志中学 陈满和

解答物理习题的思维起点，可以从选取研究对象为基础，从物理过程寻找突破口，以物理概念为依据，以物理规律为途径，建立物理模型，移植解题模式，找出解题关联点，不同物理习题其思维起点不同，选择合适的解题思维，物理问题可获顺利解决。

物理；解题思维；起点；解题途径

俗话说，万事开头难，物理解题也是这样，要顺利解答物理问题，从何着手，思维起点在哪儿？这是解题的首要问题，这就要求解题者从构成物理问题的诸多因素如研究对象、物理知识、技能、方法等特点入手，结合自己的实践经验，选择合理的思维起点，使解题思维活动迅速地从问题情境的初态活跃到终点，找出解题的突破口。本文结合具体实例，谈谈选择思维起点、寻觅解题途径的几种常用方法。

一、准确选取研究对象是顺利解题的基础

通常问题情境中有几个相互作用的物体，如果研究对象选择不当或错选，将使解题陷入困境或增加问题的难度，因此研究对象的正确选取，常常成为分析问题、解决问题的关键。

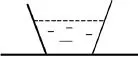
［例1］如图，一盛水的杯子放置桌面上，已知杯子的重为10N，水重为20N，杯子底面积5cm2，水面的高度为10cm。求：（1）水对容器底的压强。（2）容器对桌面的压强。

本题中有两个研究对象，杯子和水，也可以将水和杯子看成一个整体，教学中不要急于向学生讲出具体答案，要先向学生阐明研究对象的选取，做为解题的思维起点。在第一问中，应选取水为研究对象，利用液体压强公式P=ρgv进行求解，而在第二问中，就选取杯子和水为整体，利用压力和受力面积P=F/S进行求解。从上面看，选不同研究对象，采用的知识点及解题方法就不同。因此如果选错了研究对象，就会得出错误的答案，看来选取正确的研究对象是解答本题的关键步骤。

二、从物理过程着手思维，寻找突破口

物理学是“以物思理”的科学，明确问题情境中的物理过程是解题的关键，各种物理现象在各个过程中都有它特殊的运动形式，各个过程之间既互相联系又相对独立，只有过程明确，才能把握问题的本质。把物理过程先弄清楚，是解题的第一步骤。

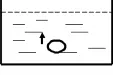
［例2］如图，在一个装水的容器中，把一个乒乓球压入水中，然后放手，问乒乓球上升的过程中水对乒乓球的压强变化？

本题中乒乓球的运动过程分段是解题的关键，大部分学生没有弄清楚乒乓球的运动过程分段，只讨论乒乓球在水中上升过程，没有分析乒乓球上升至水面的运动过程，导致得出错误的答案：水对乒乓球的压强不变。

三、选择物理概念为思维起点，寻求解题的依据

这一类型题目主要考查学生对物理概念的理解、掌握情况，要求对物理概念的内涵和外延的认识要透彻，理解要深层次，并能迁移、拓宽，把基本概念做为解题的思维起点，从基本物理概念出发，寻找解题的思路，不要死套公式。

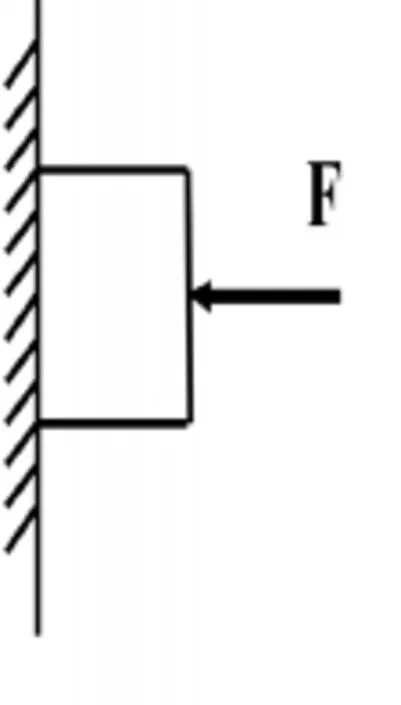
［例3］如右图，水平面上放置一物块，物重为G，在其上面施加一压力F，物块与水平面的接触面积为S，求水平面受到物块的压强？

此题考查压强的计算公式，但初中生做题时喜欢直接套用压强公式P=F/S，而得出错误的答案。教师应引导学生的思维，从基本概念出发，重视基本概念的理解，把基本物理概念做为解题的思维起点。在压强公式里，指出F为接触面的压力，而不要看到题目就死套公式，而得出错误的答案：P=F/S。如果从基本概念出发，其接触面的压力为F+G，就可得出正确的答案为P=F+G/S。又如下面例子：竖直墙上用力F压住一物体，如图，接触面的压力为F而不是G。教会学生从物理概念出发思考物理问题是很重要的。

四、以物理规律为思维起点，明确解题途径

物理规律是物理学的支柱，是构成物理学的重要内容，是命题的根本依据，掌握物理规律是解决这类问题的根本。所谓物理规律，简单地说，就是由物理实验总结或由实验和教学推证出的一些物理量之间的制约关系。对规律的掌握是指对规律所研究的对象的表达形式、适用范围等全面的理解、活化应用。初中学生对于物理规律及公式的理解往往不够深刻，看到题目，找出已知量，直接就套用公式，死套公式，没有考虑规律的对应性及具体性，从而得出了错误的答案。

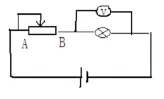
［例4］如图所示，当移动滑动变阻器的滑动触头从A端移到B端，电压表的示数和小灯泡亮暗的变化情况是（）

A.V示数变小，灯变亮。

B.V示数变大，灯变亮。

C.V示数变小，灯变暗。

D.V示数变大，灯变暗。

本题考查了串联电路的电阻、电压、电流变化规律。灯泡的亮度取决于灯泡的实际功率，通过判断灯泡的实际功率来判断灯泡的亮度变化。依题意：当滑片从A向B端滑动时，连入电路的电阻变短，电阻减小。电源电压不变，根据I=U/R，电流增大，灯泡的电阻不变，电压增大，根据U’=I’R，灯泡的电压增大，电压表的示数增大，灯泡电压增大，电流增大，根据P’=U’I，求得灯泡的功率增大，灯泡变亮。让学生学会根据规律分析是解题的根本。

五、揭示物理模型为思维起点，移植解题模式

物理问题千变万化，诸多试、习题是由一些典型的物体模型演变而来，揭示并建立物理模型就是在一定条件下突出问题的本质因素，忽略非本质因素，把熟知的原始模型进行合理的移植，并利用处理这些模型的科学方法，使问题得到顺利解答。

［例5］一弹性小球从水平速度V0飞向倾角为θ（θ＜45°）的弹性斜面上，如图3所示，设小球与斜面碰撞时无机械能损失，且碰撞时间不计，问经过多次碰撞后小球回到原入射点共经历多少时间？（设斜面足够长）

图3

读罢此题，仔细辨析，联想两个熟知的物理模型，一是弹性碰撞（过程模型），另一个是匀减速直线运动（运动模型），由于小球与斜面碰撞无机械能损失，而碰撞后小球的运动很复杂，碰撞次数很难确定，但沿斜面方向上小球运动的加速度大小总等于重力加速度的分量a= gsinθ,方向与初速度v0沿斜面方向分量vx=v0cosθ的方向相反，因此，小球复杂的运动可视为在斜面上做初速度为v0cosθ，加速度为-gsinx的匀减速运动，而匀减速运动的位移——时间公式s=υ0t-1/2at2和s=0可得：，解得

六、找出联系，建立思维起点，抓住解题关联点

物理知识之间都是互相关联、互相渗透，有密切的联系，而在联系的交结处就会出现联系点，这些联系点常常起到“桥梁”之作用，从联系点着手，常常使解题者思路畅通，出奇制胜。

［例6］如图4所示，物块M以速度v0竖直下落时，物体m在水平面上的运动的速度为多大？

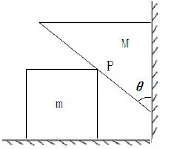
图4

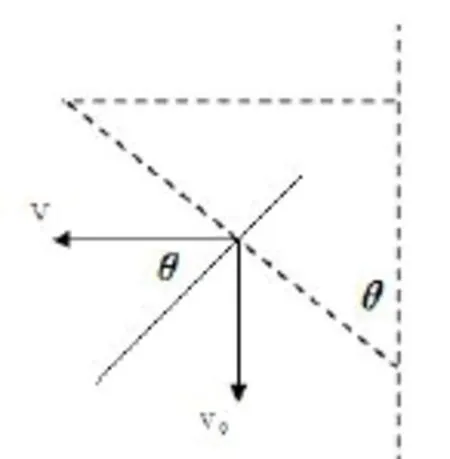
图5

本题情境是两物体在同时运动时始终互相接触，接触点P参与了两种运动，一种是沿斜面向上，另一种是沿水面向左。在此过程中两物体虽然沿接触面方向（即斜面方向）有相对运动，但沿垂直于接触面（即垂直于斜面）方向的速度分量大小相等，由图5所示知

υcosθ=υ0sinθ，即υ=υ0tgθ

由以上可见，物理习题千变万化，不同的习题，其思维起点不尽相同，即使同一道习题也可选择不同的思维起点。由于习题的千差万别，解题思路并没有固定的模式，但无论通过哪种思维方法获得问题解决，思维突破口相当重要，起点不同，解题繁简、难易程度不同。“良好的开端是成功的一半”，不是没有道理的，只有选准思维起点，解题才可获顺利解决。

（责任编辑：詹国荣）