例谈解析几何试题赏析
◎福建省福州市屏东中学 徐劭毅
例谈解析几何试题赏析
◎福建省福州市屏东中学 徐劭毅
俗话说“爱美之心,人皆有之”,可对于数学之美,喜之者却颇为鲜见.数学欣赏之所以困难,固然有数学抽象难懂的原因,但缺乏对课本以及试题的深入探究也是不容忽视的因素.本文以解析几何试题为例,从定义、解法、思想方法、本质内涵等四个角度,阐述数学试题赏析过程.
数学思想;赏析试题;美;圆锥曲线
我国现代著名数学家徐利治教授提出:“所谓数学美的含义是丰富的,如数学概念的简洁性,统一性;结构系统的协调性,对称性;数学命题与数学模型的严谨性,普遍性;还有数学中的奇异性等等,都是数学美的具体内容.”其实,作为自然科学的最基础学科,数学美并非“阳春白雪,曲高和寡”,我们可以从多个途径去感受、欣赏数学之美.
解析几何是用代数方法研究几何图形的一门学科,正是由于用的是代数方法研究几何,故它可以与向量、三角、函数等知识自然融合.从不同的视角欣赏解析几何试题,可以充分体会数学美中有理,理中有美.
赏析视角1:赏析定义之美
椭圆与双曲线的第一定义和方程之间就是“和”与“差”的区别;标准方程的推导过程也存在很大的相似;圆锥曲线在极坐标下的统一方程,这些都反映了他们之间具有统一美.此外,从椭圆的定义类比到双曲线的定义,不是简单地从“和”类比到“差”(双曲线的一只),而要加“绝对值”;圆锥曲线第二定义都是“到定点和到定直线之比”,仅仅是这个比值差异决定了曲线的不同种类,这些都体现了圆锥曲线的奇异美.椭圆与双曲线方程在推导过程中引入“b”以后,使得方程更加简洁,而且能够明确体现它们之间的几何性质;抛物线方程在引入“p”以后,其方程性质更加简明,这充分反映了圆锥曲线在方程结构上的简洁美.

赏析:本题以圆锥曲线曲线C为题干,并没有指明是哪类圆锥曲线,故要分类讨论.由于抛物线只有一个焦点,故分类讨论的落脚点即:椭圆中= 2a=4k+2k=6k;双曲线中,这充分体现了圆锥曲线的奇异美.而离心率的计算公式均为,这又再次体现了统一美.以上分析充分体现了圆锥曲线的统一美与奇异美.
例2.设F为抛物线y2=4x的焦点,A,B,C为该抛物线上三点,若FA+FB+FC=0,则
A.9 B.6 C.4 D.3
赏析视角2:赏析解法之美
“数学是思维的体操”,她在逻辑性与思维性上有着独一无二的奇异特性.在学习数学过程中,解题扮演着举足轻重的地位.如何解题,如何用最合适的方法解题可以展现不同层次的数学思维水平.
例3.设m∈R,过定点A的动直线x+my=0和过定点B的动直线mx-y-m+3=0交于点P(x,y),求 PA·的最大值.

赏析:欣赏数学真善美的一个途径是:梳理思想并领略抽象数学模型的智慧结晶.该题,看似无从下手,仔细分析后可得:根据题中两条直线互相垂直,可得点在以线段为直径的圆上,如右图所示.再由勾股定理以及基本不等式可得答案.本题通过构造圆这个模型,将直线、圆、勾股定理巧妙地联系起来,充分体现了数学之美渗透于数学的知识、结构和解法中.
例4.已知椭圆E经过点A(2,3),对称轴为坐标轴,焦点F1,F2在x轴上,离心率(Ⅰ)求椭圆E的方程;(Ⅱ)求∠F1AF2的角平分线所在直线l的方程;

赏析:(Ⅰ)问用待定系数法即可.(Ⅱ)问的关键在于求出kl.以下提供三种方法。可以采用角平分线的性质定理求出直线l与x轴交点的横坐标,进而求出直线方程;也可以设∠F1AF2=2a,可以求得tan2a,再采用二倍角公式,求出tan2a,由此推出kl;当然最妙的一种方法是由椭圆的光学性质,直线l即椭圆在点A处的法线.由于可以求出椭圆在A(x0,y0)处的切线故这道题的第(Ⅱ)问用了3种不同的方法,第一种是几何的方法,第二种是代数运算的方法,第三种是根据圆锥曲线的物理性质,可谓各有千秋,充分体现了数学思维之美.
赏析视角3:赏析思想方法之美
例5.设双曲线C的中心为点O,若有且只有一对相交于点O、所成的角为 60°的直线和使,其中和分别是这对直线与双曲线C的交点,则该双曲线的离心率的取值范围是().
数学思想方法较之数学基础知识具有更高的层次和理性的地位,它是一种数学意识,属于思维和能力的范畴,用于对数学问题的认识处理和解决.数学思想方法是数学知识的精髓.常见的数学思想主要有:数形结合,分类讨论,函数与方程,转化与化归,特殊与一般等等.数学思维方法将把思维、数学思维、数学发展中的发现、发明与创新的思维过程作为自己的研究对象.数学的思维方法主要有三种:类比,归纳和演绎.
赏析:任何一个解析几何问题的解决都是通过几何图形代数化与代数结果几何化实现的,其核心思想是“数形结合”.这道题若采用设直线斜率,利用弦长公式计算,会很繁琐.如果结合双曲线的图像以及双曲线的渐近线,便由题意很快得知渐近线斜率的范围,由此求出离心率的范围.这题考察了数形结合的思想,不落俗套,富有内涵.
(Ⅰ)求椭圆E的方程;(Ⅱ)设动直线l:y=kx+m与椭圆E有且只有一个公共点P,且与直线x=4相交于点Q.试探究:在坐标平面内是否存在定点M,使得以PQ为直径的圆恒过点M?若存在,求出点M的坐标;若不存在,说明理由.

赏析:(Ⅰ)问用椭圆定义即可.注意到(Ⅱ)问中的直线x=4为该椭圆的右准线.问题的结论:在坐标平面内存在定点M(1,0),使得以PQ为直径的圆过定点M,而M正是椭圆的右焦点.这是巧合吗?事实上,经过推广(类似于这道题的证明)可以得到以下结论:椭圆的右焦点为,设动直线l:y=kx+m与椭圆E有且只有一个公共点P,且与直线相交于点Q.则以PQ为直径的圆恒过F2(当然还可以改为左焦点F1,此时对于的直线变成其逆命题是否成立?
例7.如图,F1(-c,0),F2(c,0)分别是椭圆=1(a>b>0)的左,右焦点,过点F1作x轴的垂线交椭圆的上半部分于点P,过点F2作直线PF2的垂线交直线于点Q;(Ⅰ)若点Q的坐标为(4,4),求椭圆C的方程;(Ⅱ)证明:直线PQ与椭圆C只有一个交点.
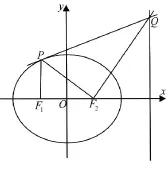
赏析:①例7第(Ⅱ)问恰巧为例6第(Ⅱ)问的逆命题.将其推广到一般情况即为:椭圆的右焦点为F1,P,Q分别是椭圆和椭圆右准线上的点,且PF1⊥QF2,则直线PQ与椭圆有且只有一个公共点P.
②例6,7充分体现了研究数学问题的一种思维方式:从特殊到一般进行推广,再思考其反面.实际上,很多数学问题都是由此产生的.当进行数学研究时,看到这样一些令人欣喜的结论,不也是一种美感吗?
赏析视角4:赏析本质之美
赏析数学试题的本质,即是对数学知识背景,数学本源的赏析,对数学思想方法的把握,对数学思维方法的感悟,对数学之美的鉴赏等等.
在圆锥曲线中,有些几何量如斜率、距离、面积、比值和变量无关,这类问题统称为定点,定点问题.这类问题我们要从“变”的现象中发现“不变”的本质,从“不变”的本质中探究“变”的规律.
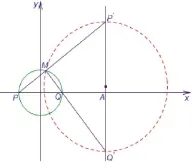
第(II)问看似平淡无奇,实际上有着其平面几何背景.在此题的证明过程中,可以发现:虽然点M在圆上动,以及由M带动的两个动点P′,Q′也在动,但是两个动点P′,Q′的纵坐标之积始终为定值,即AP′,AQ′是个定值.记以P′Q′为直径的圆与x轴的交点为H1,H2,则由圆的相交弦定理可得到结论:AH12=AH22=AP′·AQ′.由于AP′·AQ′是个定值,即AH1,AH2均为定值.再由于A为定点,故点H1,H2即为以P′Q′为直径的圆C′经过的定点.
综上,这道题还可以得到以下两个副产品:①以P′Q′为直径的圆C′的圆心C′与M的连线与圆O相切(1个公共点);②AP′·AQ′是个定值.
由以上分析可得:圆的相交弦定理就是这类题目的本质.得到圆的优美结论后,那么与圆相近的椭圆也成立这样的结论吗?经过研究,依然可以得到:已知椭圆与x轴交与A,B两点,垂直于x轴的直线l过定点Q(m,0)(m>a),P是椭圆O上异于A,B的任意一点,若直线PA交直线l于点M,直线PB交直线l于点N,则①QM·QN是一个定值;②以MN为直径的圆C总经过定点;③直线CP与椭圆只有一个公共点.
世间万物,以真善美为最高境界.数学自然也有自己的真善美.欣赏数学的真善美,是数学教育的一项重要任务.但是,数学的真善美往往被淹没在题海里,需要大力挖掘,用心体会才能发现、感受、体验与欣赏.
(责任编辑:王钦敏)

