初中数学教学目标从“双基”到“四基”的转变策略

◎福建省罗源滨海学校 郑文毅

初中数学教学目标从“双基”到“四基”的转变策略

◎福建省罗源滨海学校 郑文毅

在贯彻实施新课标“四基”课程目标导向的过程中，必须继承“双基”中的优良做法，摒弃陈旧的观念和不良的教学习惯，逐步实现从“双基”教学到“四基”教学的有益转变．

双基、四基、继承、发展

《义务教育数学课程标准（2011年版）》提出的“四基”课程目标，将“数学的基础知识、基本技能”的“双基”目标，发展为“数学的基础知识、基本技能、基本思想、基本活动经验”的“四基”目标.但在日常教研交流中，笔者发现有两个现象，一个是很多老师对何谓“四基”还不甚了解，另一个是部分老师认为“四基”的提出就是完全否定过去的“双基”目标导向.换句话说，我们很多老师并没有真正了解：为什么要把“双基”发展成“四基”？“四基”对学生的基础教育培养又有何意义？基于此，就如何继承“双基”中的优良做法，以及如何把握数学基础教育发展的方向，归纳了如下几点看法，希望有助于摆正我们数学基础教育教学的前进方向.

一、继承“双基”教学中的优良传统

在数学的课堂教学中，加强基本知识和基本技能的教学，是我们数学课堂长期的实践中总结下的精华，启发式教学是我们初中教师最擅长使用，也是最得心应手的教学方式之一，这都是值得我们继承的.那么在实际的教学中，有哪些具体的做法是我们要弘扬与发展的呢？

1.温故而知新

学生对于未知领域的知识内容是很感兴趣的，我觉得把新知识的学习建立在旧知识的基础上，既方便于学生对新知识的理解和掌握，也方便老师更好地组织教学.比如在教《锐角三角函数（1）》(人教版九下)时，为了更好地温故知新，我就改变了背景陌生且叙述冗长引例，先让每个学生拿出一副三角板来研究边、角关系，并复习已学的旧知识：

（1）三角板的各内角度数；

（2）直角三角形两锐角互余；

（3）直角三角形30°角所对的边是斜边的一半；

（4）等腰三角形两腰相等；

（5）勾股定理.

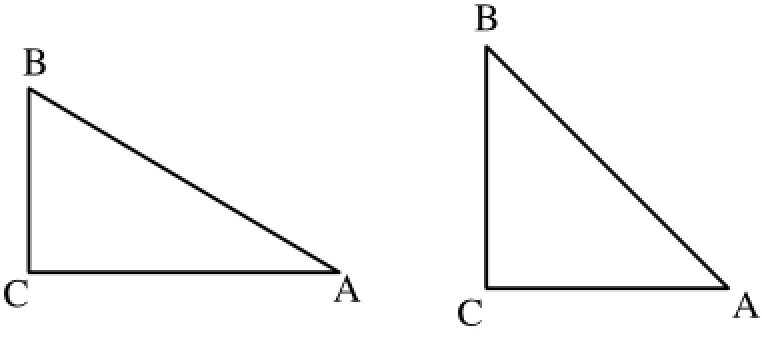
在旧知识一一呈现后，我就和学生一起归纳：问题（1）、（2）是直角三角形内角之间的关系，问题（4）、（5）是直角三角形边之间的关系，那（3）讲的是什么呢？学生在前面的铺垫下略加思考懂得回答.接着我再用红色粉笔把（3）中的“角”和“边”这两个关键词划出来，时机成熟了，“锐角三角函数”研究的就是直角三角形边与角的关系.趁着学生一声似懂非懂的“哦”，我继续往下说，直角三角形中的一个锐角（比如∠A）有三条边与之对应，分别是对边、邻边、斜边，那三条边两两的比值有6种比值：，而这就是这个锐角的六个三角函数.因为有了旧知引出新知的铺垫，在实际的授课中，我的学生不仅会掌握初中的三角函数内容，还会饶有兴趣的自学了高中的两个三角函数.

“温故而知新”的教育原则，正是我们数学课堂教学所要传承的典型方法，也是我们数学教师最为精心设计的一个部分.因为它符合学生的认知规律，使学生由旧知中产生困惑，形成一个情境来激发探求新知的欲望，从而能很好地让学生经历了新知识的发生和发展过程，学生在这样子的环境中学习，会感到既轻松又有效.这无疑是“双基”教学中一个精华的、有效的做法.

2.加强变式教学

我觉得加强例题的变式教学也是继承“双基”教学的一个优良传统.变式教学作为课堂教学活动的一个重要环节，可以将一道题目进行变化或适当地拓展，给学生提供一个发展思维的阶梯.这不仅拓展整个课堂教学的空间，也避免了题海战术，真正起到事半功倍的效果.比如我发现学生对公式的记忆大多很机械，若我能在授课时让学生在有限的时间内看到尽量多的公式变形形式，并在各种形式中寻找不变的规律，这样不仅能帮助学生记忆公式应用公式，也能培养学生化归能力.在教《平方差公式》（人教版八上）时，我举了如下例子：下列式子能否用平方差公式计算,并指出公式中的a、b分别是什么？

（1）（2m+n）（2m-n）；（-2m-n）（2m-n）；（-2m+n）（-2m-n）；（-2m-n）（2m+n）.

（2）（2m+n+3）（2m-n-3）；（-2m-n-3）（2m-n+3）；（-2m-n-3）（2m+n+3）.

通过上述形式的变化能够加深学生对公式的理解，在变化的式子中让学生发现并掌握公式的本质特征：平方差公式应用时公式中的a，b与顺序无关，相同项即公式中的a，相反项即公式中的b.学生只要找出相同项和相反项，然后把相同项的平方减相反项的平方，问题就解决了.

变式教学注重知识间内在的关联，强调学科知识的系统构建.因此，例题的变式教学当然是“双基”教学中又一个优良的做法.但要让它发挥更大作用，还要通过学生逐步地体验与积累，比如尽可能通过学生的合作交流，在解题后还要进行归纳和反思，以挖掘问题的本质，并揭示规律，这样才能形成学生自己的基本技能.

3.注重课堂教学小结

刚接触新的数学知识，学生难免没有方法，若老师只是用大量的练习来训练，让学生在不断地碰壁与失误中总结经验，那代价未免太大了.如果我们老师能充分利用课堂小结环节的作用，帮助学生梳理知识脉络，进而与其它知识融会贯通，势必会产生事半功倍的效果.比如充分利用图表、口诀、框架等记忆方法进行课堂小结，有效地做到了巩固复习、记忆和反馈功能，这在数学教学的实践证明是行之有效的.所以注重课堂小结是“双基”教学中又一具体表现.另外，注重课堂练习巩固也是我们“双基”教学的突出特色之一，比如在每节数学课堂中，当新知识建立后，我们就会趁热打铁地安排巩固训练.因为数学的概念、命题、公式、法则的理解与应用，都需要通过各层次题目的反复训练达到的，所以这种夯实基本功的做法收到的效果是有目共睹的.

其实双基教学就是我们课堂中最为基本、最应当要强调的东西，如：温故知新、加强课堂练习巩固、加强变式教学、注重巩固小结等.注重基本教学是我国现在数学教育鲜明的特色，也是我国千百年来所提倡的优良传统.

二、实现“双基”教学到“四基”教学的转变

1.“双基”为什么要发展为“四基”

数学基础教育中，“双基”教学的作用和其历史贡献值得肯定的.2001年颁发的《基础教育课程改革纲要（试行）》规定课程应达三维目标：知识与技能、过程与方法、情感态度与价值观.而新《义务教育数学课程标准（2011版）》提出了四维目标：知识与技能、数学思考、问题解决、情感态度.不管是三维还是四维目标，“双基”仅仅涉及到“知识与技能”的目标，而新增加的“两个基础”则涉及另外的目标——过程方法、数学思考和情感态度等.可以说，发展成“四基”是多维数学教育目标的要求.

“双基”在实施过程中往往出现“见物不见人”的现象，而教育必须以人为本.所以我们在教学中，除了要让学生掌握必备的基本的数学知识和技能外，还要在课内注重渗透数学的基本思想，积累数学活动经验.新增加的“两个基础”就直接与人相关，也符合“素质教育”的理念，所以发展成“四基”也是提高学生数学素养的基本要求.

2.实现从“双基”到“四基”的发展性转变

①达成启发式教学与探究式教学的有效融合

启发式教学是我们教师在讲解中永远应该弘扬的传统，现实的数学课堂，以发问方式启发、引导学生学习知识和发展能力，已成为数学教师主流的教学行为.但也出现重形式提问，重结果启发，重外在情境启发等现象.随着新课标对数学探究教学的强调，特别是新教材中，几乎每个课时都创设了探究活动，这对我们现行的课堂教学触动很大.所以，如何达成启发式教学与探究教学间有效的融合，是摆在当前课堂教学的一大问题.我觉得要做好两个方面的工作：一是创设好有启发作用的问题情境，可以用生活中实例来构建数学模型，也可以用纯数学的旧知来引导学生；二是充分利用学生资源做好探究活动，如引导学生经历观察、试验、猜测、验证、推理概括等过程.比如：在学习八年级数学《13.2画轴对称图形（2）》时，我先让学生在平面直角坐标系中画出点A（2，3）、点B（-4，-1）关于x轴的对称点，然后引导学生观察点A与、点B与这两对对称点间横、纵坐标的关系，并归纳出关于x轴对称点的坐标特点.接着让学生用类比的方法画出点A、B关于y轴的对称点，并自行归纳出关于y轴对称点坐标的特点.最后让每个小组在讨论中总结了点（x，y）关于x轴、y轴对称的一般规律，并用这一规律完成练习：已知点P（2a+b，-3a）与点（8，b+2），若点P与关于x轴对称，求a、b的值；若点P与关于y轴对称，求a、b的值.在我的引导和启发下，学生自己去探索、合作，并获得结论，从中探究一条“从特殊例子得出一般结论，再用结论去解决特殊问题”解决数学问题的方法.

达成启发式与探究式在教学上的有效融合，我们需要关注操作层面上求同存异和互为补充，力求趋于一致.课堂上我们要提倡教师善于启发、引导，与学生“合作”，也要关注学生自主或合作交流完成对数学问题的主动探索.

②积累基本活动经验，感悟基本思想

数学活动经验是学生经历了具体的活动而形成的，既有感知的内容，也可以是反思后的经验.比如：在九年级数学《24.1.4圆周角（1）》中，由于圆心角的位置固定不变，而圆周角随顶点的位置变化而变化，要探究同弧所对圆周角与圆心角的三种位置关系，要先让学生经历动手画图、操作、体验等具体的数学活动，在感知的基础上学生发现二者的数量关系.接着再引导学生利用三角形及等腰三角形的性质加以证明.在这个过程中我们应鼓励学生去自己探索，自己获得结论.在学生积累一定的数学基本活动经验的基础上，就可以“悟出”一些数学思想，比如分类讨论思想、化归转化思想.

数学是思维的科学，发展学生的数学思维能力是中小学数学教学的重要任务.我们数学教学在发展数学思维能力方面有两个特色：一是数学思想方法的渗透，二是解题教学的变式训练.数学思想在课堂教学中的渗透，首先是将数学思想是融于数学知识、技能和方法之中的，正如上面的教学；其次，数学思想的获得是通过理解、提炼、总结、再理解、应用等循环过程，让学生逐步“悟”出数学思想.

③强调基本的概念教学

基本的概念教学，是数学课程教学的主要内容之一.学生如果没有掌握好数学基本概念及其内在联系，常常会造成数学运用能力不强，也就造成学习成绩无法提高的现象.所以我们要强调基本的概念教学，在教学中我们要充分地挖掘概念的内在联系，并从中寻找解题的思路.比如函数概念的学习，如果直接要求学生从之前的静态问题转变为运动变化问题，这对学生而言是有困难的.所以我们要做好各方面的联系，比如函数图像是让学生体会数形结合的思想方法；基本初等函数的二维空间的思考模式，使学生的数学思维更为活跃；三角函数成为学生研究三角形以及周期变化的重要工具.我们老师要做的是让学生的大脑扩充或提升新数学知识体系，并重新认识已学内容的观点.

开启学生的思想智慧，发展学生的创新意识与创造力，是数学教育的根本目标。实现新课标“四基”课程目标，需要继承传统“双基”教学的优良做法，也要懂得摈弃陈旧的观念和不良的教学习惯。

（责任编辑：王钦敏）