根据数学问题特征 多向深化解题反思

◎福建省大田县第六中学 郑为勤

根据数学问题特征 多向深化解题反思

◎福建省大田县第六中学 郑为勤

在数学教学中，深化解题后的反思，需要抓住问题的差异性，反思审题要点；抓住问题的多解性，反思策略生成；抓住问题的共性，反思通性通法；抓住问题的多变性，反思内涵外延；抓住问题的拓展性，反思规律模型构建，从而引导学生不断地积累解题经验，深刻理解数学解题思维的全过程．

解题；引导；反思；经验

众所周知，解题前的探索，解题后的反思，是解题教学中培养和提高能力的两个不可缺少的环节.解题反思虽然不是一个新鲜的话题，但在笔者的教学观察中，解题后的反思在师生心目中的地位远不如解题前的探索重要，往往浅尝辄止，未能深入进行反思.造成这种现象的原因是多方面的.从教师方面看，教师虽然认识到培养学生反思意识的重要性，但教学时间有限，教学任务繁重，留给学生解题后反思的时间和空间很少.从学生方面看，学生受学习习惯、学习态度的影响，只追求“速度”和“数量”，只为完成作业而解题，不重视“质”的提升.笔者结合实际案例，谈谈如何引导学生在解题后进行深入反思，从而不断积累解题经验.

一、抓住问题的差异性，反思审题要点

数学试题是命题者精心打磨的，每一个字或条件都深含命题者的用意.在考试时，学生往往会遇到似曾相识的题目，以定势思维论处，结果“会而不对”.究其原因——粗心大意，没认真审题.因此在教学时，引导学生抓住题目“相似”中“不相似”的部分进行反思，用圈点、划线强化审题，审出“不同”和“要点”，为解题扫除障碍，培养学生思维灵活性、严谨性.

案例1：若抛物线y=mx2-6x+3与x轴两个不同的交点，求m的取值范围.

教学中，笔者展示某位学生的解答后，把学生分两派，对答案“m＜3”和“m＜3且m≠0”展开辩论.在交流中有同学认为这个解答是正确的，理由是“当b2-4ac＞0时，抛物线与x轴两个不同的交点.”而认为这个解答错误的同学理由是“我发现当m=0时，抛物线变成y=-6x+3是一次函数，它与x轴的交点只有一个不符合题意.”“必须把m=0除外，函数y=mx2-6x+3才是二次函数.”“当二次函数二次项系数为字母时，要兼顾二次项系数不为0.”“m≠0是这个题目的隐含条件.本题正确答案应是m＜3且m≠0.”

学生们的发言非常精彩，把以上几位同学的发言总结起来就是对这道题的辨析.在激辩中，学生逐渐从模糊变得清晰，从“纠错”上升到“究错”，m的取值范围由m所处的位置而定.老师此时不需要多说什么了，只要提供以下题组，留给学生去思考就可以了.

题组：（1）二次函数3x2-6x+m=0与x轴有两个不同的交点，求m的取值范围；

（2）二次函数mx2-6x+3=0与x轴只有一个交点，求m的取值范围；

（3）二次函数mx2-6x+3=0与x轴没有交点，求m的取值范围；

（4）若函数mx2-6x+3=0与x轴有交点，求m的取值范围.

解题过程中，学生常常受思维定势影响，墨守成规，不能洞察题目条件的“微变化”，不能及时调整解题方法，酿成“会而不对”的后果.因此当学生解题碰上其中的某一小题时，教师在解题后适当变式呈现题组，抓住问题的差异引导学生反思，对提高学生的辨别能力是有非常有效的，能很好促进学生构建知识网络.

二、抓住问题的多解性，反思策略生成

问题的多解性指的是一个问题的几种不同答案，或是用不同的思路、方法、知识解决相同的问题.在学生解题后，老师应提醒他们不能就此罢休，而是进一步反思，探索能不能一题多解？在所有解法中，哪一种解法是最好、最简捷的？为什么？这样的反思，可以让学生对问题有更深层次的理解，开阔了视野，为灵活解题提供了保证.

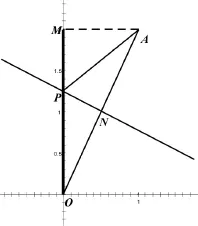
案例2：在平面直角坐标系中，已知点A的坐标为（1，2），点P的坐标为P（0，y），当OP=PA时，求y的值.

在有限的时间里，更多的学生只想了一种方法.而通过学生展示，教师点评，收获了解题的思路和方法.教师引导学生及时整理以下两种方法：

法一：（数的角度）根据已知OP=AP=y，通过Rt△AMP勾股定理列方程，解得y的值.

法二：（形的角度）由两角对应相等证△ONP～△OMA，得比例式代入解得线段OP的长，进一步得y的值.

通过解题后反思，学生学会从“数”的角度、“形”的角度去思考，开拓思路.比较这两种方法的同时，明确它们适用的范围.从而建构、形成自己的解题风格.在试题讲评中，学生呈现许多解法中，有非常考验毅力的“通法”，也有奇思妙想的“妙法”，它们都是数学思维的大餐，此时一定要引导学生反思同一问题不同解法的区别和联系，归纳总结不同方法适用的题目特征.通过多解性的反思，达到提高分析能力、灵活解题的目的.

图（1）

三、抓住问题的共性，反思通性通法

在解题教学中，题目背景不一样，解题方法却大同小异，这也是我们常说的多题一解.近几年中考常出现通过图形变换，某些结论保持不变，而解题的思路和方法类似，甚至完全相同的几何综合题.在解此类题目后，引导学生抓住问题的共性，便能快速而精准地找到对应题型的解法，从而达到解一题通一类.

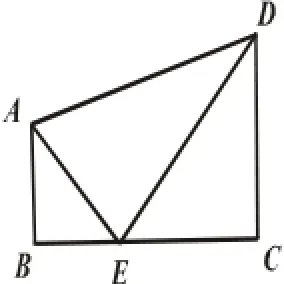
案例3：如图（2），梯形ABCD中，AB∥DC，∠B=90°，E为BC上一点，且AE⊥ED.若BC=12，DC=7，BE：EC= 1：2，求AB的长.

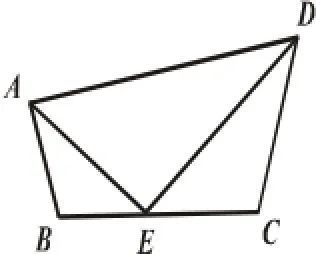
笔者在学生解题后以“追问”的形式引导学生展开反思.“回顾解题过程，未能求线段AB的长的同学是哪一步推理没有想到？”“你们认为本题的解题关键是什么？”“我们是怎么证明三角形相似的？”“当这一组三个相等的角不是直角，而是锐角（如图（3））、钝角（如图（4））时，三角形是否还会相似？”“你能从中发现这一特殊问题特征的解题规律吗？”

图（2）

图（3）

图（4）

这三个图形改变的是角度的大小，不变的“三个角相等”.解题后，引导学生反思题目的共性——“一线三等角”，反思共性问题的解题通法，反思共性问题常与其他知识相结合的所有可能性.在解题时，只要识别出基本图形（共性），题目便可轻松获解.

四、抓住问题的多变性，反思内涵外延

在解题教学中，教师经常对试题进行变式训练，如改变图形、弱化条件、条件与结论互换等等.解题后，引导学生抓住问题的多变性，多角度、多方位揭示数学核心知识的内涵外延，可以调动学生解题的兴趣和积极性，让不同层次的学生得到不同的发展，让学生体验和感受知识间的关系，实现知识的融会贯通.

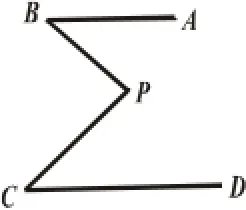
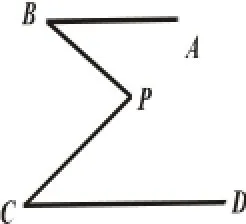
案例4：如图（5），已知AB∥CD，求证：∠BPC=∠PBA+∠PCD.

图（5）

图（6）

图（7）

图（8）

通过适当添加辅助线，过点P作AB的平行线，或延长BP交CD于E，或连结BC等，可以得∠BPC=∠PBA+∠PCD.然而如果此题只停留在会证，便偃旗息鼓、鸣金收兵，就“登堂”而未“入室”，没有充分发挥此题的功效.如何能抓住本题的图形、结论可变性引导学生反思，达到“事半功倍”的效果呢？

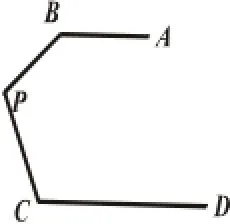
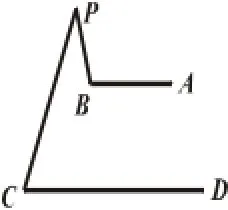
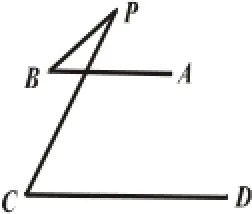
笔者在学生们解完题目后，要求“如果题中AB∥CD这一条件不变，请尝试在课堂练习本上画出不同于图（5）的点P的位置.并与同伴交流.“学生画图并通过交流得到其余三种不同的点P的位置.如图（6），图（7），图（8）.接着，师生开始探究各图中∠APC与∠PAB、∠PCD的关系.得出结论：图（5）中∠APC+∠PAB+∠PCD=，图（6）中∠PAB=∠APC+∠PCD，图（7）中∠PCD=∠PAB+∠APC.在学生们经历对图形变式后解题的过程，请学生对解题思路、方法做总结.他们发现当图形发生变化时，解题中添加的辅助线、所用的知识点、推理的过程都大同小异，但结论却发生了变化.

继续将图（5）中点P改变为图（9），图（10）的情况，探索各图中∠P1、∠P2、∠P3、∠P4、∠P5与∠A、∠C的关系.此时有的学生甚至能猜测，推广到一般情形，如图（11），以直线l为界的右边的角之和等于左边角的和.

图（5）

图（9）

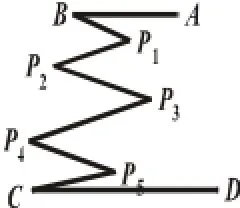
图（10）

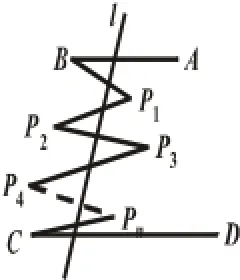
图（11）

解答此题后，引导学生反思横向变化，点P的位置（左右、上下、内外）；纵向变化，点P个数的增减，通过解系列题，发现解题方法的类似，结论微变化.“类比”是中学数学中一种重要的数学方法.由于对合情推理的考查需要，很多中考的证明题、探究题都着力从“方法不变性”与“结论不变性”入手编制.很多题目乍一看图形不同，条件变化，但解决问题的着手点是一样的.抓住题目的可变性进行反思，这类问题就成了学生的“老朋友”——熟悉的很，那么顺利解题就不在话下了.

五、抓住问题的拓展性，反思模型构建

解题受阻时，计算量、思维量受到前所未有的挑战，解题也一时陷入“山穷水尽”，百思不得其解.在老师的点评后，学生却大呼“坑人”，解题出现了“柳暗花明”.解此类题后，引导学生抓住问题的拓展性和延伸性，反思解题思路的破解，揭示此类题目的解题规律，从不同角度构建数学模型.

案例5：如图（12），点C（2，-3）是抛物线y=x2-2x-3上一点，点D横坐标取值范围是-1≤x≤2，试确定当△ACD的面积最大时点D的纵坐标？

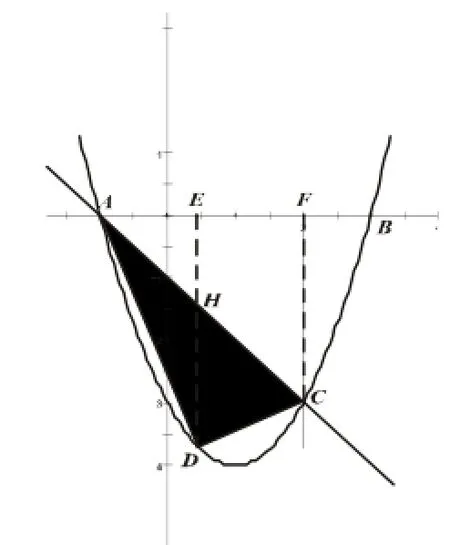
图（12）

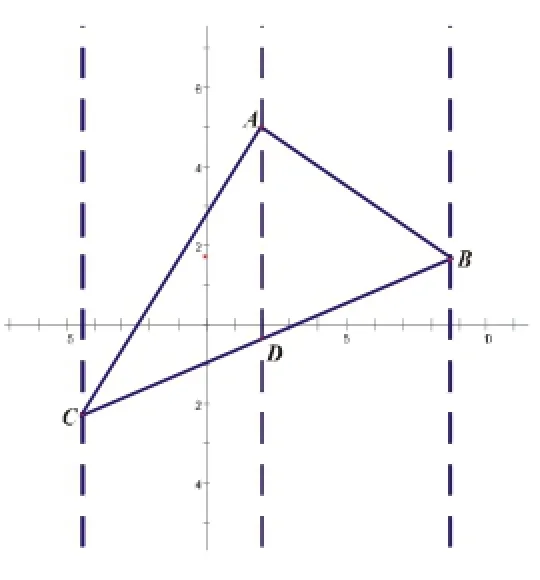
图（13）

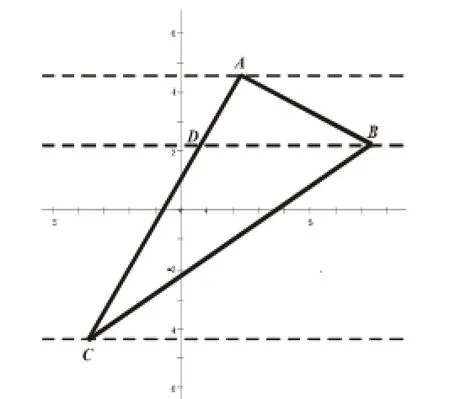
图（14）

点D是动点，△ACD的面积随着点D横坐标的变化而变化.这个题目的解题关键是找到变量△ACD的面积与变量点D的横坐标的函数关系式，多数学生采用“割补法”表示△ACD的面积.

法一：围成矩形减去三个直角三角形面积;

比较三种不同的解法，法三计算量最小，是最简捷的.但当笔者发现，法三中△ACD的面积通过整理等于·DH·AE，与三角形面积公式完全吻合时，笔者决定引导学生继续对此题作进一步反思.

通过观察、猜想、验证，学生们找到了一种计算三角形面积的新方法，如图.或如图学生们为找到这个一般性结论欢欣鼓舞.此题蕴藏的玄机，若不是解题后的反思，就被错过了.对可伸展性问题的反思，学生的推理能力、钻研精神得到培养.对于相当一部分学生来说，他们对数学的兴趣和探索的潜能将延伸到课外去，从中得到美的享受.

在数学教学中，用心挑选或设计典型的例题、练习，在解题后，引导学生深入反思可以让学生不断积累解题经验，养成优秀的数学思维品质.

（责任编辑：王钦敏）