开放式基金投资策略选择
——基于随机优势理论及区别函数分析
●宁波大学商学院 燕小青
开放式基金投资策略选择
——基于随机优势理论及区别函数分析
●宁波大学商学院 燕小青
本研究利用模型限制较少的随机优势理论与区别函数构建了正确率达到75.9﹪的投资策略,使投资人可以运用少数关键因素来建立基金投资策略从而避免面对多重准则无所适从的现象。研究结果表明,二阶随机优势理论适用于我国资本市场,可以明确地将基金分类为效率和非效率两种类型;基金规模与买进周转率这两种基金属性具有区别基金绩效的能力,且区别函数的正确归类率也较高。
开放式基金 随机优势理论 区别函数
一、引言
证券投资基金已有一百多年的历史,是资本市场最富有活力的金融工具之一。我国首支开放式基金华安创新自2001年起开始发售至今已有13年的历史,国内开放式发展迅速和规模也远超过封闭式基金成为市场主流,截止2012年底已有一千多只。但并不是所有的基金管理公司经营绩效都能达到预期,如2012年嘉实基金旗下社保组合28股被套,投资失败率达80%。因此,投资人选择最优基金时既应考虑净值或收益排行,也应考虑基金的报酬和风险指标。然而,综观过去研究,无论是单因子或是多因子模型,本质上仍是以CAPM作为理论基础,但CAPM模型的假设普遍受到学术界质疑 (Skrepnek and Sahai,2013)1。故有学者采用限制条件较少的随机优势理论模型来决定基金的绩效分类。虽然许多研究均验证了随机优势理论具有区分基金绩效的能力(Jan and Hung,2003;Kjetsaa and Kieff,2003;Meyer et al.,2005)2-4,但此类研究主要是针对基金绩效的多个属性进行的单独检测,目的是了解某个基金的属性与绩效是否显著相关,研究结果通常是同时有多个基金属性与基金绩效显著相关。他们的研究表明,如果投资人要遵循随机优势理论必须同时考虑多个基金属性,以对数量众多的基金进行投资,但面对多个基金属性的投资人最后将无所适从。基于此,本文以我国基金管理公司所发行的一般开放式基金为目标,利用不同模型来探讨报酬和风险的关系,以期建立简便的投资策略,使投资者可能遭受的损失降至最低,并评选出具备稳定报酬的基金,以提供给基金管理委员会参考。
二、文献综述
(一)利用资本资产定价模型评估基金绩效的研究。早期,投资组合绩效评估皆以Treynor(1965)5、Sharpe(1966)6、Jensen(1968)7开发的资本资产定价模型(CAPM)为理论基础。但随后诸多学者质疑该模型的解释能力,一些学者对传统模型进行了改良 (Fama and French,1993;Jegadeesh and Titman,1993;Carhart,1997;Otten and Bams,2004)8-11。首先,Fama和French认为基于CAPM模型的系统风险并不足以解释资产报酬,因此提出了三因子模型;其次,Jegadeesh和Titman提出动能投资策略的观念,认为买进过去相对强势的股票,并卖出相对弱势的股票,将为投资者带来超额报酬,为日后四因子模型奠下基础;再次,Carhart利用Fama和French的三因子模型,再加入Jegadeesh和Titman的动能效果因子,组成四因子模型。最后,Otten和Bams以Carhart四因子模型为基础,探讨了随着基金管理者获取公开信息的时间增加,改变其投资组合所形成的条件模型比非条件模型的解释能力要好。
然而,无论是单因子或是多因子模型,本质上仍是以CAPM作为理论基础,必须符合模型假设:①投资报酬率须呈正态分布;②投资人具有二次多项式的效用函数,其一阶导为正,二阶导数为负。朱波、宋振平(2009)的实证研究发现,我国开放式基金报酬并非呈正态分布12。且Skrepnek和Sahai(2013)研究发现只有风险规避者的效用函数一阶导为正、二阶导数为负,但基金市场中投资者的风险偏好并非均为风险规避者1。因此,这些假设不符合我国证券市场的实际情况。
(二)利用随机优势理论评估基金绩效的研究。随着CAPM模型的失效,Levy和Kroll(1979)13提出了以累积机率为观点的随机优势理论法则已为众多研究者使用,并陆续发展出一阶(FSD,Quirk and Saposnik,1962)14、二阶(SSD,Hader and Russell,1969)15、三阶(TSD,Whitmore,1970)16随机优势法则,这些法则可将众多的投资组合区分为有效率及无效率两种。其中,FSD法则可区分基金投资组合是否有效,且不需假设投资人效用函数,因此即适用于风险规避者也适用于风险追逐者,是初步删除无效组合的标准;SSD法则假设投资人的效用会随着财富的增加而递减,故SSD法则仅适用风险规避者;利用TSD法则,假设投资人为递减的风险规避者,即财富水平越高时投资人风险规避程度越低,故TSD效率集合由SSD效率集合选取组成。此外,由一阶、二阶及三阶的筛选过程可知,SSD效率集合是FSD效率集合的子集合,TSD效率集合由SSD效率集合选取组成,故SSD法则最可能选出有效率的投资组合。
随后,已有学者利用三种法则检验了基金属性和绩效的相关性。Jan和Hung(2003)首先选用1961年至2000年美国CRSP基金数据库的16435支开放式基金资料,按照标准普尔分法根据基金的投资策略分成24类(股票型6类、平衡型1类、债券型6类、抵押型1类、货币型4类和其它型6类),在将各类型基金按照(有无借贷、规模大小、周转率高低、费用高低及过去绩效好坏)五种属性分为五项对照组,最后采用随机优势模型(SSD法则)探讨了各类型基金与对照组基金绩效的优劣。随机优势模型衡量结果显示,以无借贷、规模大、周转率高、低费用率及前期绩效优的大部分基金表现较佳2。随后,Kjetsaa and Kieff(2003)扩展了Jan和Hung的研究,他们利用随机优势理论 (FSD法则、SSD法则及TSD法则)衡量1985年至1999年共377支开放式基金的绩效,先将观察期间区分为1985—1999、1985—1997与1985—1995三种情况,在分别利用三种随机优势法则筛选无效率绩金,最后和道琼斯威尔夏5000指数及标准普尔500指数的报酬进行比较。结果显示,道琼斯威尔夏5000指数与标准普尔500指数报酬衡量的效果较好,尤其是股票型开放式基金比随机优势理论衡量的更有效。但随机优势理论的二阶(SSD法则)及三阶(TSD法则)的衡量也有效率,能够区分基金的有效性3。与他们的研究不同,Meyer等(2005)主要衡量增加国际投资组合是否带来了风险分散的效果,并对随机优势理论与M-V(Mean-Variance)法则进行比较。数据源有五种组合,第一种组合为新西兰6种资产国内型组合,第二种组合为新西兰4种、澳洲3种及香港3种国际投资组合,第三种组合为第二种组合再加上6种日本投资组合,第四种组合为第二种组合加上6种英国投资组合,第五种组合为第二种组合再加上3种英国及3种日本投资组合。结果显示,M-V法则能够发现增加国际投资组合可带来风险分散的效果,但随机优势理论中只有二阶(SSD法则)及三阶(TSD法则)具有发现风险分散和区分投资组合优劣的能力4。
从上述分析可知,多数情况下二阶 (SSD法则)及三阶(TSD法则)均有效,具有区分投资组合优劣的能力。但在考虑Levy(1992)提出三阶随机优势理论的算法不恰当17,另外,各阶带有无风险资产的随机优势对本研究并无有效的区分效果,故我们仅采SSD作为实证研究的法则。
(三)影响开放式基金绩效的因素研究。在Sharpe之前对开放式基金的研究着重于基金整体绩效,这样仅能帮助投资者了解基金绩效的优劣,并无法作为投资者遴选开放式基金的标准。因此,Sharpe(1966)最早研究发现基金手续费和绩效呈负相关6,随后学者们纷纷针对影响基金绩效的因素进行研究,以寻求基金本身属性与绩效之间的关系。如Ippolito(1989)选用1971年至1984年共128支开放式基金资料,运用横截面回归模型分析销售费用、管理费用、其他费用(总费用减去管理费用)和周转率对基金绩效的影响。结果显示,销售费用与基金绩效呈正相关,管理费用、其他费用和周转率与基金绩效无显著相关18。Grinblatt和Titman(1994)19、Carhart(1997)10与Ippolito的研究方式和结果均类似。Grinblatt和Titman选用1974年底至1984底共209支开放式基金数据,运用横截面回归模型分析基金规模、其他费用、管理费用、周转率和销售费用对基金绩效的影响。结果显示,销售费用和周转率与基金绩效呈正相关,管理费用与基金绩效呈负相关,基金规模和其他费用与基金绩效无显著相关。Carhart选用1963年1月至1993年12月共1892支开放式基金,运用横截面回归模型分析基金管理费用、交易成本、基金规模、销售费用和买卖周转率对基金绩效的影响。结果显示管理费用、交易成本、销售费用和卖出周转率与基金绩效呈负相关,基金规模和买入周转率与基金绩效无显著相关。随后一些学者扩展了上述研究,其中Golec(1996)20、Prather和Bertin等(2004)21在研究中分别加入了新的因素,Dahlquist和Engstrom等(2000)22、Jan和Hung(2003)2分基金类型进行了实证检验。具体而言,Golec选用1988年至1990年共530支开放式基金,运用横截面回归模型分析基金经理人特征(年龄、任期、教育程度及具备MBA学位与否)与基金绩效的相关性。另外在模型中加入基金交易费用、管理费用、周转率、团队规模、发行年数和基金规模等可能的影响因子。实证结果显示,经理人任期、MBA学位和管理费用与基金绩效呈正相关,交易费用和经理人年龄与基金绩效呈负相关,经理人教育程度、周转率、团队规模、发行年数和基金规模与基金绩效无显著相关。随后,Prather和Bertin选用1996年至2000年5000支股票型开放式基金,依投资目标分为7种类型,并将基金属性分成4大类25小类,运用横截面回归模型分析基金属性和绩效之间的关系。结果显示样本基金绩效不具备持续性,且成本收益的比率、现金流量账面价值的比率与基金绩效呈正相关,基金规模、基金费用、经理人管理基金数与基金绩效呈负相关。此外,Dahlquist和Engstrom等将基金分为股票型与债券型,选用1992年至1997年共210支瑞典开放式基金,运用横截面回归模型分析现金流量、基金规模、周转率、管理费用及交易量对基金绩效的影响。结果表明,交易量与基金绩效呈正相关,管理费用与基金绩效呈负相关。然而对基金规模而言,股票型基金的基金规模与基金绩效呈负相关,但债券型基金的基金规模与基金绩效呈正相关。Jan和Hung依标准普尔分类方法将基金分为股票型、平衡型、债券型、抵押型、货币型和其它型等6大类,选用1961年至2000年共16435支开放式基金数据,采用随机优势模型(SSD法则)分析销售费用、基金规模、周转率、其他费用和过去绩效对基金绩效的影响。实证结果显示:①整体基金规模与基金绩效呈正相关,但其它型基金结论却相反;②整体周转率与基金绩效呈正相关,但货币型基金结论却相反;③整体过去绩效与基金绩效呈正相关,但债券型基金结论却相反;④整体其他费用与基金绩效呈负相关,但债券型基金和其它型基金的结论却相反;⑤整体有销售费用的基金优于没有销售费用的基金,但在平衡型、债券型、抵押型和货币型基金方面,没有销售费用的基金却优于有销售费用的基金。
从上述研究结果可见,基金规模、基金经理费率、基金保管费率、买进周转率、卖出周转率、交易费用率、基金成立年数及基金经理人更换次数等八项因素是基金绩效的直接影响因素。基于此,本文将以这些因素为基础,利用SSD法则研究我国开放式基金的策略选择是否恰当。
三、开放式基金投资策略模型设计
(一)SSD演算过程。随机优势理论相对于M-V法则及CAPM模型效用函数的限制较少,并对于任何机率分配不作假设,也常运用在基金绩效评估中。然而Levy(1992)指出三阶法则(TSD法则)的算法有一定偏颇,建议使用一阶或二阶来进行实证研究17,主要是因为这两种法则足以得到令投资人满意的效率投资组合。由于鉴于一阶法则(FSD法则)区分效果较低,故本研究利用二阶随机优势法则(SSD法则)作为基金绩效评估的方法。
本研究设定有m(i=1,2,3……m)个投资组合,每个投资组合皆有n(j=1,2,3……n)个季报酬率观测值,且观测值均为非连续样本,故假设各个观测值出现的机率相同,即f(Xj)=1/nf(Xj),n为每个投资组合中观测值的个数。演算时,由于SSD效率集合是FSD效率集合的子集合,因此我们先利用FSD演算法则构建季报酬率矩阵,随后再利用SSD法则对上述季报酬率矩阵进行转换并相互比较以选取最佳投资组合。具体过程如下:
首先,利用FSD演算法则将每一种投资组合中的n个季报酬率观测值依次递增排列构成新的矩阵,表示为[xij]mn,使得xi,1≤xi,2≤xi,3…≤xi,n,其中第i种投资组合如果优于第一种投资组合,那么对所有的季资料观测值j(j=1,2,3……n)符合下式:
xi,j≥x1,j,且至少有一个不等式成立 (1)
接着将矩阵内的m列数据进行两两比较,如符合式(1)则删除第一列的投资组合,如不符合则均保留。依此类推,最后保留的是效率最佳投资组合。
其次,运用SSD法则进行演算,即以FSD演算法已排序过的矩阵[xij]数据为基础进行转换。具体而言,新矩阵数据中每一列数据转换如下:

其中第i种投资组合如果优于第一种投资组合,则所有的季资料观测值j(j=1,2,3……n)都符合下式:

随后将矩阵内的m列数据进行相互比较,如符合式(2)则删除第一列的投资组合,如不符合则均保留。依此类推,最终保留的是最佳效率投资组合。
(二)运用区别分析建构基金投资策略。区别分析主要是了解基金间的差异,即先利用区别变量建立区别函数,再利用区别规则对个体做出分类以预测个体属于哪种群体。本研究采用典型区别分析法进行分析,该方法的优势是不需要假设数据为正态分布就可以得到区别函数。简言之,我们首选需要选择一些变量作为区分数据类别的依据,随后将随机优势理论所得结果进行区别分析,并将结果设定为两类:第一类“1”为无效率基金;第二类“2”为有效率基金。在选择区别变量时,根据前人的研究成果,将基金绩效的直接影响因素分为八类,即基金规模、基金经理费率、基金保管费率、买进周转率、卖出周转率、交易费用率、基金成立年数及基金经理人更换次数等,并将这8种因素进行筛选以得出最适合进行基金有效性判断的因素。
四、开放式基金投资策略的实证研究
(一)样本选择。本文以2010年到2012存在的87只开放式基金为研究对象(变量均采用季度数据),这些基金在2010年7月1日前已经成立,且至2012年6月30日仍未清算或遭同业合并的一般开放式国内股票型基金。在该样本期间中国股市相对稳定,基金市场的投资具有一定规律,能够满足我们对当前中国基金市场投资选择有效性的判断。本文的买进周转率、卖出周转率等相关数据通过各基金管理公司在其指定信息披露媒体上所公布的数据计算得到,基金经理人更换次数根据基金经理任职与离职信息计算得到,其他数据均来自聚源数据库、中国基金网和国泰安数据库。
(二)变量定义
1.基金绩效评估的变量定义。借鉴Jan和Hung(2003)的研究,我们采用开放式基金季净值报酬率来评估基金绩效。开放式基金季净值报酬率的计算方式是:Rp,t=。其中Rp,t是第p只开放式基金第t季报酬率,MFNAVp,t是第p只开放式基金第t季净值,MFNAVp,t-1是第p只开放式基金第t-1季净值,Cp,t是第p只开放式基金第t季所发放的现金股息。
2.基金绩效影响因素的变量定义。基金绩效影响因素包括基金規模、基金经理费率、基金保管费率、买进周转率、卖出周转率、交易费用率、基金成立年数及基金经理人更换次数等八种(如表1),其中基金規模是指开放式基金每季所管理的净资产平均数;基金经理费率是指开放式基金每季经理费用率的平均数;基金保管费率是指开放式基金每季保管费用率的平均数;买进周转率是指开放式基金每季买进周转率平均数;卖出周转率是指开放式基金每季卖出周转率平均数;交易费用率是指开放式基金每季交易费用率平均数;基金成立年数是指开放式基金成立年数;基金经理人更换次数是指开放式基金更换基金经理人次数。
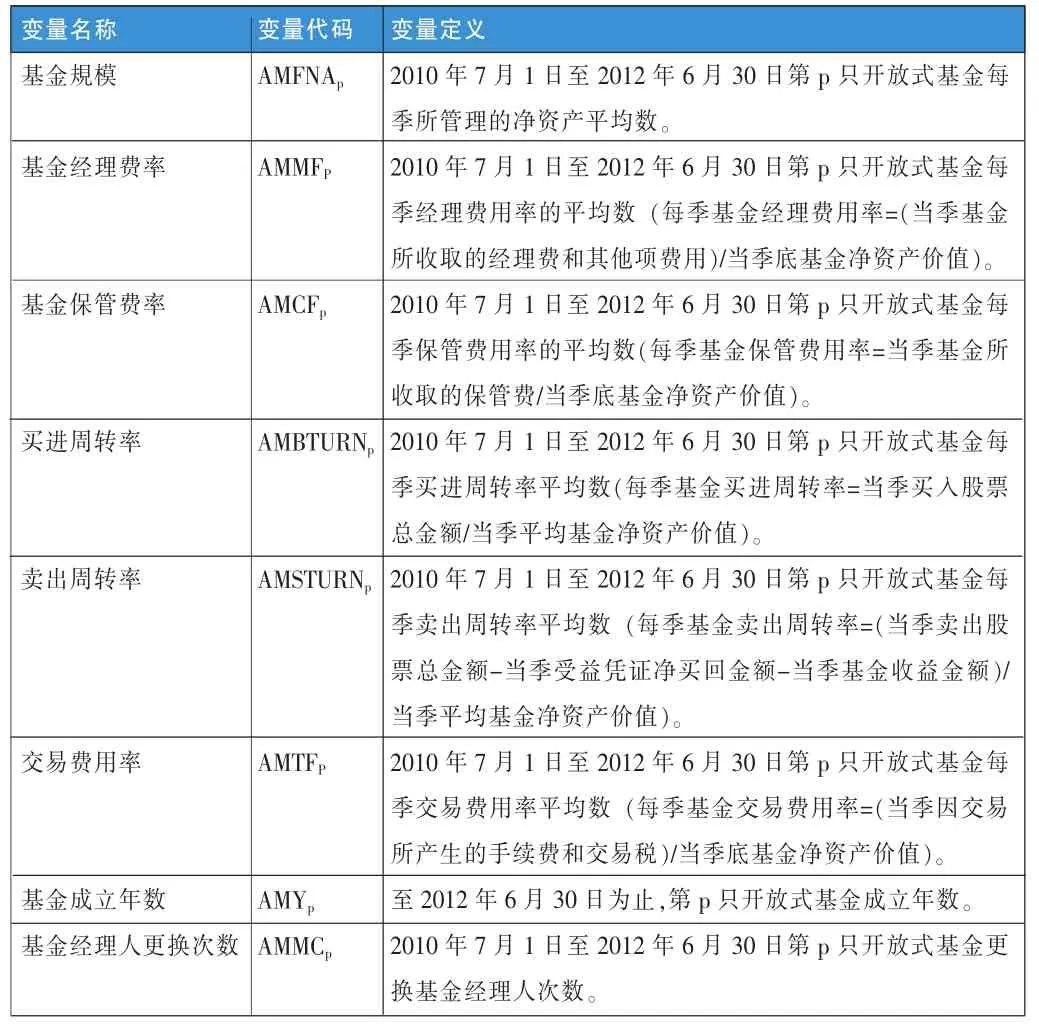
表1 基金绩效影响因素的变量定义表
(三)描述性统计分析。由表2可知,我国基金发展迅速,基金規模AMFNAp的均值为5230000000,基金成立年数AMYp的均值也有6年,可见已初具规模。且在2010年7月1日至2012年6月30日间虽基金经理人更换次数AMMCp的最大值多达6次,但均值却为2.2667次,显示大多数公司的人员基本稳定,更换在正常范围内。AMMFp与AMCFp的均值分别为0.4866与0.8932,表明我国大多数基金公司收取的基金保管费率均大于基金经理费率,当前基金保管费是基金公司的主要收入来源之一。而AMTFp交易费用率的均值为0.1171,与基金保管费率、基金经理费率相比较小,表明我国基金公司的利润空间较大。AMBTURNp与AMSTURNp的均值分别为0.7450、0.9200,最大值分别为1.1100、1.1500,这意味着大多数基金公司买卖交易非常频繁,投机行为严重且基金风险较大,但该指标并未显现投资效率,本文需利用SSD法则进一步进行分析。
(四)实证结果分析
1.二类样本共变量矩阵一致性检验。首先,利用二阶随机优势理论(SSD),将87只一般开放式股票型基金分类为有效率及无效率两种,研究发现不具第二阶随机优势的基金有77支基金,具第二阶随机优势的基金有10支基金(由于篇幅所限,本文没有列出87只基金分别归属的类别)。将不具第一阶随机优势列为第1类,具有第二阶随机优势列为第2类。
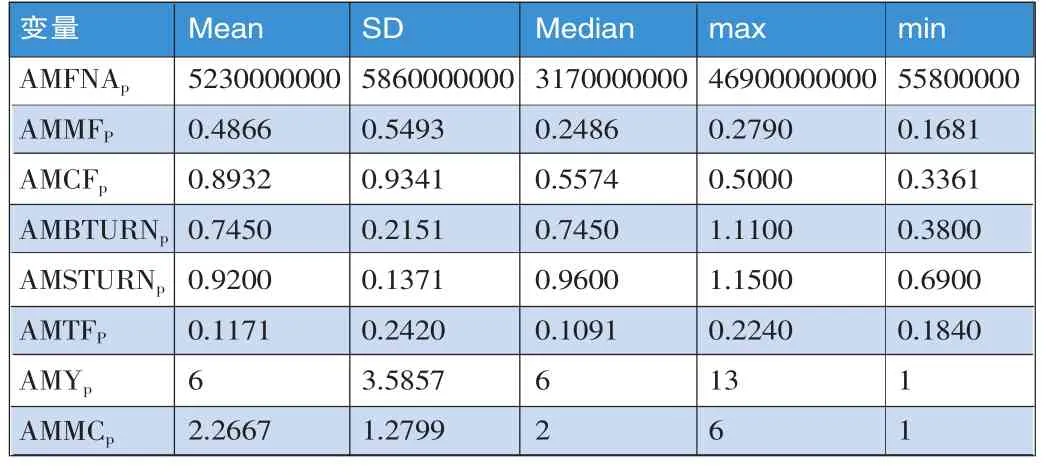
表2 变量描述性统计分析
其次,将已分好的随机优势理论结果(即无效率为1类,有效率为2类)进行样本共变量矩阵一致性检验(如表2),以确认样本是否从同一母体获取。该表结果显示,此二类样本为同一母体,即p值为0.336不显著,适合进行区别函数分析。
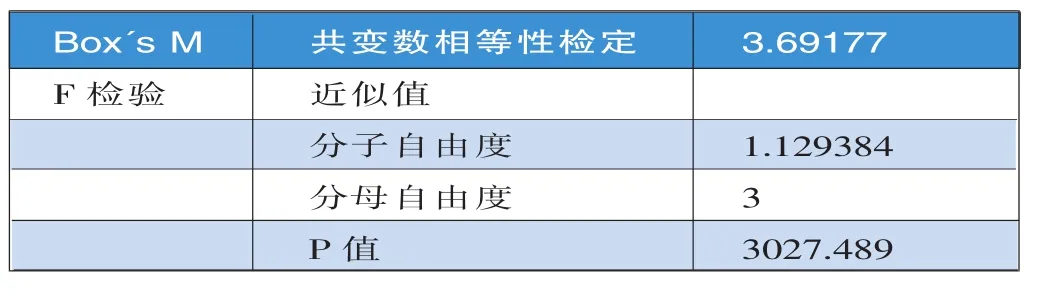
表2 相等母群共变数矩阵的虚无假设检定表
2.区别变量效果能力检测。为了检测理论上适合作为区别变量的八种因素是否真的具有区别效果能力,我们利用各组平均数的相等性检验和逐步统计分析两种方法进行检验判断。
第一,进行各组平均数的相等性检定。如果观测各区别变量在非效率组1及效率组2中的平均数不相等,则代表该变量具有区别效果能力。如表3所示,仅买进周转率(AMBTURNp)与基金规模(AMFNAp)显著,P值分别为0.088728与0.067015,而其他变量均不显著。表明仅变量AMBTURNp与AMFNAp拒绝了平均数相等的原假设,即具有区别开放式基金投资策略优劣的能力。
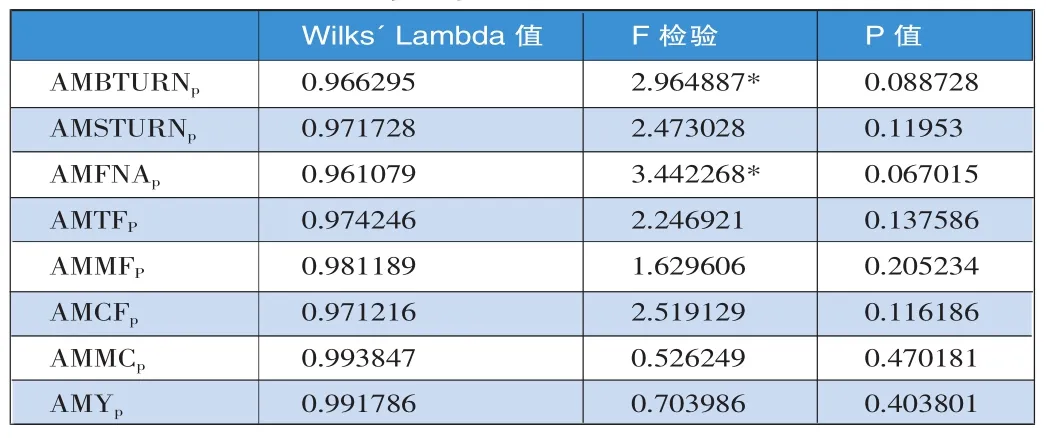
表3 各组平均数的相等性检验表Wilks' Lambda值F检验
第二,采用逐步统计的方式,将八个区别变量按区别效果能力依序带入函数中观察效果。由表4可知,在步骤1,区别变量中以AMFNAp的P值 (0.067015)小于AMBTURNp的P值(0.088728)且最为显著,即最具备区别效果,这与表3的结果相同,故首先代入。到步骤2,剩余的七个区别变量中AMBTURNp的P值 (0.003242)小于AMTFp的P值 (0.006037)与AMSTURNp的P值(0.008176),最为显著,适合作为区别变量,这也与表3的结论一致,因此将买进周转率也代入分析。最后到步骤3,剩余的六个区别变量均未显著,表明它们不适合作为区别变量。综上所述,逐步统计分析法的研究结论与各组平均数相等性检验的结论相同,均认为买进周转率与基金规模适合进行开放式基金投资策略优劣判断变量。
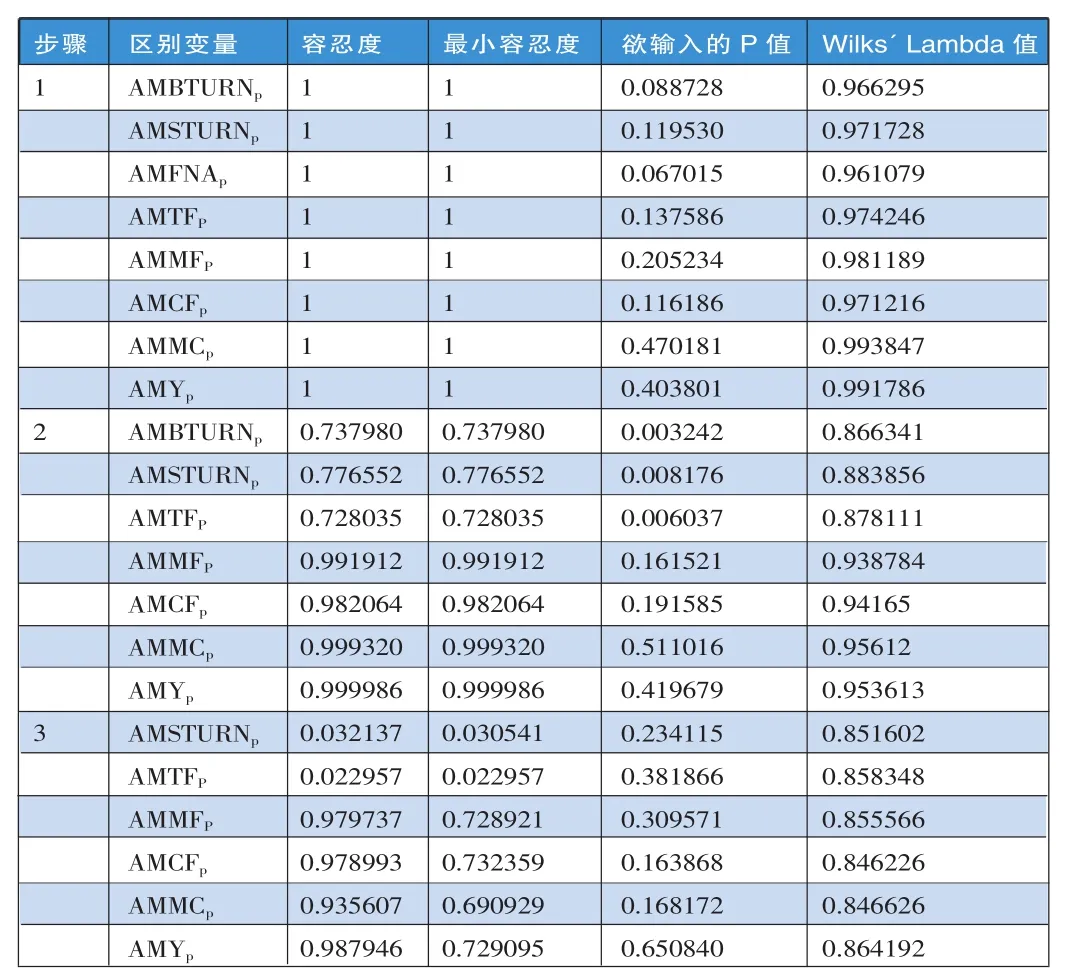
表4 逐步统计分析表
3.典型区别函数。首先,根据逐步统计分析的结果,基金规模(AMFNAp)应最先代入区别函数,然后再代入买进周转率(AMBTURNp)。因此,我们根据典型区别分析的步骤1,使用基金规模作为区别变量。随后的步骤2使用基金规模及买进周转率作为区别变量,区别变量显著性检验如表5所示。
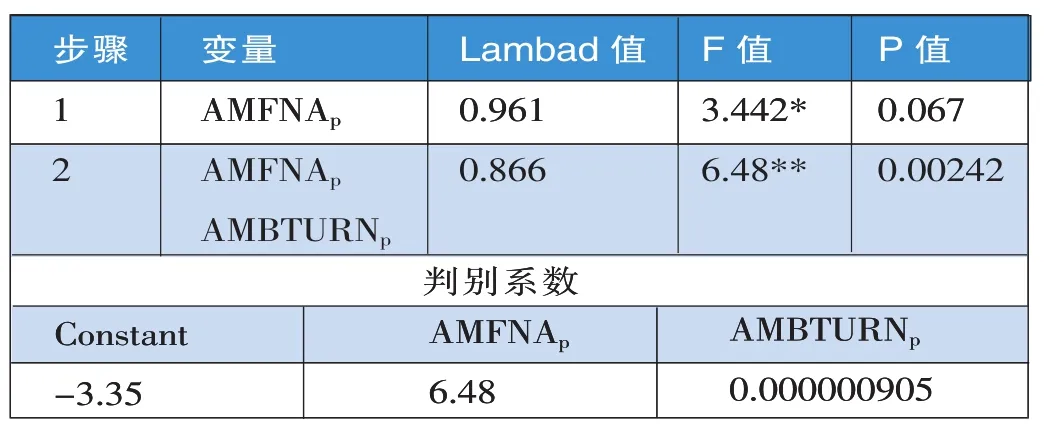
表5 区别变量显著性检验
随后依据判别系数,列出如下区别函数(其中SSD表示区别函数值):
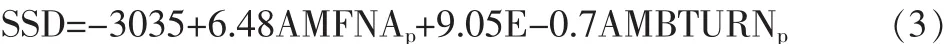
其次,为了验证上述区别函数的正确性,本文采用正确分类机率演算法进行验证(如表6)。从该表可以看出,有74﹪的SSD无效率集合被正确分类;90﹪的SSD有效率集合被正确分类,总体来说有75.9﹪的原始组别观测值已正确分类,这表明本文所构建的判别函数比较符合实际情况。
最后,本文利用上述正确分类机率表来预测各组开放式股票基金个数(如图1、图2)。其中,图1显示非效率组(SSD= 1)各区别函数值的个数统计。虚线左侧代表正确预测的非效率组基金个数,共有57只,虚线右侧代表错误预测的效率组基金个数,共有20只;图2显示的是效率组(SSD=2)各区别函数值的个数统计。虚线左侧代表错误预测的非效率组基金个数,共有1只,虚线右测代表正确预测的效率组基金个数,共有9只。
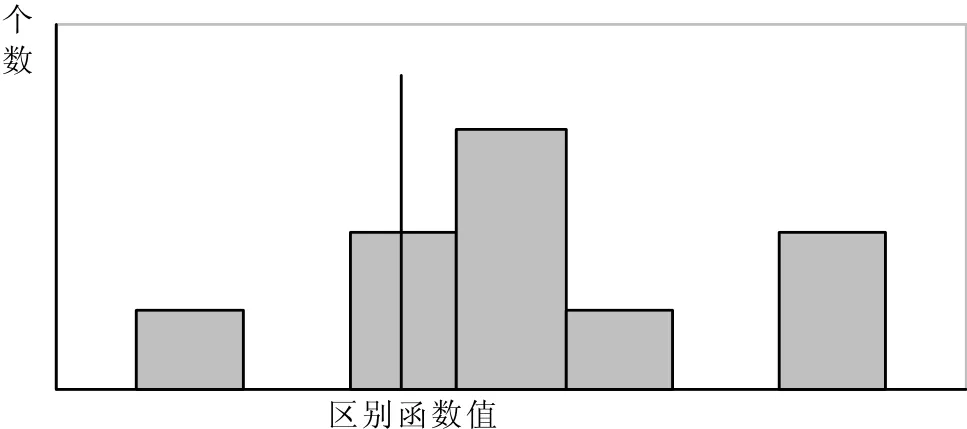
图2 效率组基金区别函数值图
五、研究结论与不足
由于资本资产定价模型争议颇多,又因为以往文献中的基金属性研究无法满足投资者对基金优劣的直接判断,故我们采用限制条件较少的随机优势理论模型来决定基金的绩效分类,利用可能影响基金绩效的因素作为自变量,采取区别分析法探讨投资人可实施的投资策略,以判断具有较佳绩效的基金。因此,本研究所建立的区别函数,将10支SSD效率集合基金及77支无效集合基金重新分类,其中有75.9﹪的基金被正确归类。如果投资者靠单纯猜测选购基金有88.5%(77/87)的概率不符合随机优势,而采取本文创建的区别函数决定基金投资策略仅26.0%的概率会把无效率基金判定为有效率,且有10%的概率会把有效率基金判定为无效率,故我们的研究结果将大幅度改善投资人的投资效率。此外,我们认为仅基金规模及买进周转率和基金效率相关,且基金效率是由基金报酬比较得知,因此这两个基金属性应该和基金报酬有关,该结论可作为未来研究的参考。
本研究受限于基金买进周转率与卖出周转率不易取得,需要在相关网站收集数据并计算得到,故仅选用了87只开放式股票基金作为研究对象,影响了判别函数的精确性。另外,也未将基金公司的投资目标进行分类分析,可能会对经营绩效产生影响。因此,后续研究可参照我们的方法收集数据并对各种不同投资目标进行分类,用以判断基金绩效的优劣。■
(本文系国家社科基金项目 “民间资本支持中小企业发现路径与对策研究”〈10AJY105〉阶段性研究成果。)
1.Skrepnek G H,Sahai A.2013.Efficient Point Estimation of the Sharpe Ratio[J].Journal of Statistical and Econometric Methods,2(4):129-142.
2.Jan,Y.C.,M.W.Hung.2003.Mutual Fund Attributes and Performance[J].Financial Services Review,12(2):165-178.
3.Kjetsaa R,Kieff M.2003.Stochastic dominance analysis of equity mutual fund performance[J].American Business Review,21 (2):1-8.
4.Meyer,T.O.,X.M.Li,L.C.Rose.2005.Comparing Mean Variance Tests with Stochastic Dominance when Assessing International Portfolio Diversifaication Benefits[J].Financial Services Review,14(2):149-168.
5.Treynor,J.L.1965.How to Rate Management of Investment Funds[J].Harvard Business Review,43(1):63-75.
6.Sharpe,W.F.1966.Mutual Fund Performance[J].Journal of Business,39(1):119-138.
7.Jensen,M.C.,1968.The Performance of Mutual Funds in The Period 1945-1964[J].Journal of Finance,23(2):389-416.
8.Fama,E.F.K.R.1993.French,Common Risk Factors in The Returns on Stocks and Bonds[J].Journal of Finance Economics,33(1):3-56.
9.Jegadeesh,N.,S.Titman,Returns to Buying Winners and Selling Losers Implications for Stock Market Efficiency[J].Journal of Finance,1993,48(1):65-91.
10.Carhart,M.M.1997.On Persistence in Mutual Fund Performance[J].Journal of Finance,52(1):57-82.
11.Otten,R.,D.Bams.2004.How to Measure Mutual Fund Performance:Economic Versus Satistical Relevance[J].Accounting and Finance,44(2):203-222.
12.朱波、宋振平.2009.基于SFA效率值的我国开放式基金绩效评价研究[J].数量经济技术经济研究,4:105-116。
13.Levy,H.,Y.Kroll.1979.Efficiency Analysis with Borrowing and Lending:Criteria and Their Effectiveness[J].The Review of Economics and Statistics,61(1):125-130.
14.Quirk,J.P.,R.Saposnik.1962.Admissibility and Measurable Utility Function[J].Review of Economic Studies,29:140-146.
15.Hadar,J.,W.R.Russell.1969.Rules for Ordering Uncertain Prospects[J].American Economic Review,59:25-34.
16.Whitmore,G.A.1970.Third Degree Stochastic Dominance [J].American Economic Review,60:457-459.
17.Levy,H.1992.Stochastic Dominance and Expected Utility: Survey and Analysis[J]Management Science,38(4):555-593.
18.Ippolito,R.A.1989.Efficiency with costly information:A study of mutual,1965-1984[J].Quarterly Journal of Economics,104(1):1-23.
19.Grinblatt,M.,S. Titman.1994.A Study of Mutual Fund Returns and Performance Evaluation Techniques[J].The Journal of Financial and Quantitative Analysis,29(3):419-444.
20.Golec,J.H.1996.The Effects of Mutual Fund Managers’Characteristics on Their Portfolio Performance,Risk and Fees[J]. Financial Services Review,5(2):133-148.
21.Prather,L.,W.J.Bertin,T.Henker.2004.Mutual Fund and Characteristics,managerial attributes,and fund performance[J]. Review of Financial Economics,13:305-326.
22.Dahlquist,M.,S.Engstrom,P.2000.Soderlind,Performance and Characteristics of Swedish Mutual Funds[J].Journal of Financial and Quantitative Analysis,35(3):409-423.

