利用L L∞+1范数的多基线相位解缠绕方法

刘会涛 邢孟道保 铮

（西安电子科技大学雷达信号处理国防科技重点实验室 西安 710071）

利用L L∞+1范数的多基线相位解缠绕方法

刘会涛 邢孟道*保 铮

（西安电子科技大学雷达信号处理国防科技重点实验室 西安 710071）

多基线相位解缠绕问题可以转化为求解L1范数优化问题的最优解，然而L1范数多基线相位解缠绕算法存在内存需求量大的问题，且对噪声严重的干涉相位图处理效果不理想。为了减少用线性规划算法解L1范数多基线相位解缠绕时内存需求较大的问题，该文提出用L∞范数的惩罚函数来近似L1范数的惩罚函数以减少优化模型中优化变量的大小，从而将多基线相位解缠绕模型其目标函数变为L∞范数+L1范数的形式，并且优化变量的大小减少了约57%。最后，通过一个噪声严重的实测数据对该文算法进行了验证，实验结果表明，该文提出的方法不仅可以有效地解缠绕质量较好的条纹图，同时对噪声严重区还具有一定的滤波效果。

干涉合成孔径雷达；多基线；相位解缠绕；L1范数；L∞+ L1范数

1 引言

相位解缠绕技术是干涉合成孔径雷达（Interferometric SAR， InSAR）完成3维地形测绘的最重要的图像处理技术，其目的是从缠绕相位中恢复出缠绕前的相位，即绝对相位。在过去的几十年中，研究者们提出了很多求解方法，这些算法基本可以被分为两类：基于路径跟踪的方法和基于优化问题的方法。然而所有的单基线相位解缠绕方法都以相位连续性假设为前提。不同于单基线相位解缠绕方法，多基线相位解缠绕方法可以利用干涉相位图的基线多样性来实现相位解缠绕。理论上，只要基线长度比是无理数，根据中国余数定理（Chinese Remainder Theorem， CRT），解缠绕相位可以很容易地计算得来［13］-。但是由于CRT算法的噪声鲁棒性较差，传统的基于CRT算法的多基线相位解缠绕算法不能实现相位解缠绕。因此对基于CRT算法的多基线相位解缠绕算法的研究主要集中在以下几个方面：首先，为了使传统的基于CRT算法的多基线相位解缠绕方法能够应用于实际问题，一些研究者提出了噪声鲁棒性的增强CRT算法。文献［4］改进了传统的CRT算法并提出了具有闭式解的鲁棒性增强的CRT算法。其次，通过聚类算法降低数据的噪声进而提高基于传统CRT算法的多基线相位解缠绕算法的噪声鲁棒性。文献［5］通过将具有相同模糊数向量的像素聚为一个类，并取类内所有像素对应的截距值的高频值从而降低噪声的影响，进而将类内所有像素作为一个整体再利用传统CRT方法进行相位解缠绕（聚类分析算法（Cluster-Analysis-based algorithm， CA）），其中，文献［6］改进了CA算法中的聚类分析的直方图包络波峰选取策略。文献［7］根据多基线中的截距数据的密度信息来提高聚类的精确度进而提高基于传统CRT方法的多基线相位解缠绕算法的噪声鲁棒性（老人星算法（Cluster-Analysis based Noise Robust Phase-Unw rapping A lgorithm， CANOPUS））。将聚类方法与鲁棒性增强的CRT算法相结合，从而可以在两方面提高传统CRT算法的噪声鲁棒性［8］。除基于CRT算法的多基线相位解缠绕算法外，研究学者还提出了一些基于统计信号处理的多基线相位解缠绕算法。文献［9］和文献［10］提出基于马尔科夫随机场（Markov Random Fields （MRFs））的多基线相位解缠绕算法的最大后验估计（Maximum A Posteriori（MAP） estim ation）的实现方法和其改进算法；文献［11］和文献［12］提出了基于最大似然估计（Maximum Likelihood （ML） estimation）和基于相位梯度的ML方法来实现多基线相位解缠绕；文献［13］结合CA算法中的聚类分析的思想提出了一种改进的基于最大似然估计方法。除此之外，文献［14］将多基线相位解缠绕问题简化为1L范数的优化问题并提出了用线性规划思想解决多基线相位解缠绕问题。本文针对传统的1

L范数的多基线相位解缠绕方法内存需求较大的问题，提出用L∞范数的惩罚函数近似1L范数的惩罚函数从而使优化变量的维度降低约57%，进而降低了算法的内存需求，并且提高了算法的运算速度。

本文首先回顾了1L范数的多基线InSAR相位解缠绕算法，并通过传统1L范数算法优化变量的维度说明了该算法内存需求较大的原因，在此基础上提出了改进算法以使相位解缠绕算法占用更小的内存，并且能够处理噪声非常严重的数据，最后通过实测数据实验验证本文提出的改进的聚类方法的有效性。

2 L L∞+1范数多基线相位解缠绕算法

对于单基线相位解缠绕技术来说，解缠绕相位首先要满足缠绕相位和绝对相位之间的关系［15］，即

其中，φ， φ分别为绝对相位和缠绕相位，k为模糊数。然而，满足此约束条件的解缠绕相位存在无穷多个；为了确定哪些解缠绕相位是符合实际地形要求的，人们引进了像素之间的限制条件，即：假设相邻像素间的绝对相位变化小于等于π，这就是所谓的相位连续性假设。在此条件下，绝对相位差可以通过缠绕相位差估计得来［16］。

其中，Δφ（i）表示相邻的第i个像素和第i+1个像素间的绝对相位差。在相位连续性假设成立的条件下，相位解缠绕可以通过对相邻像素的绝对相位梯度差进行积分获得。然而，当测绘地形剧烈变化时，相位连续性假设很有可能不再满足。解决此问题的一种办法是通过优化方法求使不满足相位连续性假设的像素数量最少时的解缠绕相位，即

其中，i和j分别表示沿x和y方向做相邻相位差，ωx和ωy为沿x和y方向的加权系数。然而，文献［17］已证明该优化问题是一个NP难问题（NP-hard Problem， NP-hard）。因此，为了快速实现相位解缠绕，人们提出了用L1-norm优化问题来近似求解式（3）所述的优化问题［18］。相应的优化模型变为

为了克服单基线相位解缠绕算法对相位连续性假设的依赖，人们提出用多基线来实现相位解缠绕。相对于单基线相位解缠绕的模型，多基线相位解缠绕的模型不仅需要每幅干涉相位图像素之间的约束关系，还需要增加干涉相位图之间的约束关系。以双基线为例，其约束关系可以表示为

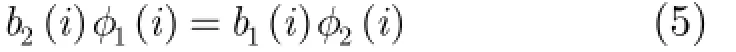
其中，b为基线长度，下标1和下标2代表不同的干涉相位图。与单基线相位解缠绕算法相比，多基线相位解缠绕算法需要考虑式（5）所示的约束条件，以双基线为例，其相位解缠绕模型变为［14］

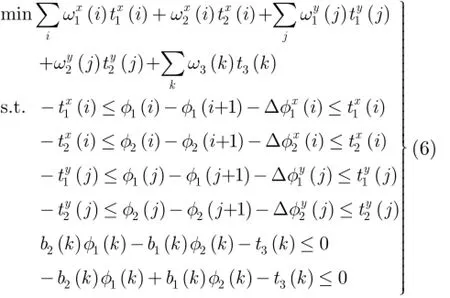
其中，t1≥ 0， t2≥ 0； i和i+1， j和j+1表示干涉相位图中沿x和y方向相邻的两个像素，k表示干涉相位图中的像素。该模型可以被简化为

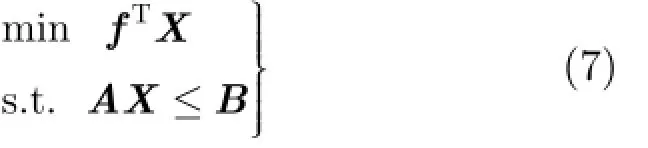
针对L1范数多基线相位解缠绕算法内存需求巨大的问题，本文提出用L∞范数的惩罚函数近似L1范数的惩罚函数以减少变量个数。具体来说就是在保留不同干涉相位图之间的约束条件对应的L1范数的惩罚函数的前提下，对相邻像素之间的约束条件用L∞范数的惩罚函数近似L1范数的惩罚函数。对于同一个优化问题而言，L1范数的惩罚函数的数学意义是使优化变量绝对和最小，而L∞范数惩罚函数是使优化变量中变量的最大值最小，此时优化变量中的所有变量均被迫趋向于0，这与L1范数的使绝对值之和最小有异曲同工之妙。因此可以用L∞范数的惩罚函数近似L1范数的惩罚函数。考虑本文提出的改进措施之后，新的优化模型中的目标函数变为L∞范数+L1范数的形式。即改进后的优化模型变为

其中，式（9）所示的优化模型中，目标函数和约束条件均为线性，因此改进后的优化模型仍然可以使用线性规划算法高效求解，且改进后的优化模型中优化变量的大小约为3MN。与式（7）所示的优化模型中的优化变量相比，改进后的优化变量的大小减少了约57%，进而在用线性规划算法求解式（9）的最优解时能极大程度降低其对内存的需求。除此之外，由于本文中提出的算法与传统的L1范数算法相比，优化变量的维度降低了约57%，在相同的线性规划算法的时间复杂度的条件下，算法的执行效率更高。

由于本文提出的算法采用L∞范数+L1范数的惩罚函数代替原优化模型的L1范数的惩罚函数，对于相邻像素之间的约束条件而言，L∞范数的约束条件比L1范数的约束条件更加放松。也就是说，采用L∞范数的惩罚函数后，在不改变目标函数最优值的前提下，φ（i）-φ（ i+1）和Δφ（i）之间容许的误差要更大一些。因此在式（9）所述的模型下，相邻像素的绝对相位差和估计相位差不再严格一致，以满足多基线相位解缠绕的L1范数强约束条件对相位的要求。也就是说，缠绕条纹和解缠绕结果反缠绕后的条纹存在不一致性，即存在滤波效果。

3 算法的性能分析

本文通过一噪声影响非常严重的双基线TerraSAR-X实测数据对本文提出的算法性能进行测试。图1（a）和图1（b）分别为短基线和长基线干涉相位图，其基线长度分别为-6.4916 m和-41.0460 m。从图中可以发现，长短基线干涉相位图受噪声的影响非常严重，大部分条纹线都被雪花地带断开。图1（c）为L1范数多基线相位解缠绕方法得到的长基线干涉相位图的解缠绕结果，图1（d）为图1（c）解缠绕结果反缠绕后的缠绕相位图。通过对比发现，该方法在条纹线清晰的地方能够非常理想地实现相位解缠绕，但是在噪声区，该算法也无能为力。图1（e）为L∞范数+L1范数多基线相位解缠绕方法得到的长基线干涉相位图的解缠绕结果，图1（f）为图1（e）解缠绕结果反缠绕后的缠绕相位图。通过对比图1（d）和图1（f），本文中提出的L∞范数+L1范数多基线相位解缠绕算法不仅对条纹线清晰的区域能够较为理想地实现相位解缠绕，而且对噪声区还有滤波作用，能够对噪声区产生干涉条纹图。

4 结束语

多基线相位解缠绕问题可以转化为求解L1范数的优化问题，并可以通过线性规划算法快速且高效地求解。与单基线相位解缠绕优化问题相比，多基线相位解缠绕技术面临数据大、信息量少的难题。为了克服L1范数多基线相位解缠绕算法在内存需求量巨大、噪声严重区性能不理想的问题，本文提出用L∞范数的惩罚函数近似L1范数的惩罚函数，并提出了L∞范数+L1范数的多基线相位解缠绕方法。与L1范数多基线相位解缠绕算法相比，本文提出的算法其优化问题中的优化变量的大小减少了约57%，因此其内存需求会更低。通过对噪声非常严重区实测数据测试发现，本文提出的算法可以有效地实现多基线数据的解缠绕，并且对噪声含有滤波效果。

图1 L1范数和L∞范数+L1范数多基线相位解缠绕结果对比

［1］ Xu Wei， Chang E C， Kwoh L K， et al.. Phase-unw rapping of SAR interferogram w ith mu lti-frequency or m ulti-baseline［C］. IEEE International Geoscience and Remote Sensing Symposium， Pasadena， California， USA， 1994: 730-732.

［2］ 靳国旺， 张红敏， 徐青， 等. 多波段InSAR的CRT相位解缠绕方法［J］. 西安电子科技大学学报， 2011， 38（6）: 97-102. Jin Guo-wang， Zhang Hong-m in， Xu Qing， et al.. Phase unw rapp ing algorithm w ith CRT for mu lti-band InSAR［J］. Journal of Xidian University， 2011， 38（6）: 97-102.

［3］ Zhang Hong-m in， Jin Guo-wang， Xu Qing， et al.. Phase unw rapping w ith Chinese Rem inder Theorem for multibaseline interferometric synthetic aperture radar［C］. Proceed ings of the 10th International Con ference on Fuzzy System s and Know ledge D iscovery （FSKD）， Shenyang， China， 2013: 93-97.

［4］ Wang Wen-jie and Xia Xiang-gen. A closed-form robust Ch inese Rem ainderTheorem and its perform ance analysis［J］. IEEE Transactions on Signal Processing， 2010， 58（11）: 5655-5665.

［5］ Yu Han-wen， Li Zhen-fang， and Bao Zheng. A clusteranalysis-based efficient multibaseline phase-unw rapping algorithm［J］. IEEE Transactions on Geoscience and Rem ote Sensing， 2011， 49（1）: 478-487.

［6］ 潘舟浩， 刘波， 张清娟， 等. 三基线毫米波InSAR的相位解缠绕及高程反演［J］. 红外与毫米波学报， 2013， 32（5）: 474-480. Pan Zhou-hao， Liu Bo， Zhang Qing-juan， et al.. M illim eter-wave InSAR phase unw rapp ing and DEM reconstruction based on three-baseline［J］. Journal of Infrared and M illim eter Waves， 2013， 32（5）: 474-480.

［7］ Liu Hui-tao， Xing Meng-dao， and Bao Zheng. A clusteranalysis based noise robust phase-unw rapping algorithm for m ulti-baseline interferogram s［J］. IEEE Transactions on Geoscience and Rem ote Sensing， 2015， 53（1）: 494-504.

［8］ Yuan Zhi-hui， Deng Yun-kai， Li Fei， et al.. Multichannel InSAR DEM reconstruction through im proved closed-form robust Chinese Remainder Theorem［J］. IEEE Geoscience and Rem ote Sensing Letters， 2013， 10（6）: 1314-1318.

［9］ Ferraiuolo G， Pascazio V， and Schirinzi G. Maximum a posteriori estimation of height profiles in InSAR imaging［J］. IEEE Geoscience and Rem ote Sensing Letters， 2004， 1（2）: 66-70.

［10］ Ferraioli G， Shabou A， Tupin F， et al.. Multichannel phase unw rapping w ith graph cuts［J］. IEEE Geoscience and Remote Sensing Letters， 2009， 6（3）: 562-566.

［11］ Pascazio V and Schirinzi G. M ultifrequency InSAR height reconstruction through m aximum likelihood estim ation of local p lanes parameters［J］. IEEE Transactions on Im age Processing， 2002， 11（12）: 1478-1489.

［12］ Fornaro G， Pauciullo A， and Sansosti E. Phase d ifference-based mu lti-channel phase unw rapping［J］. IEEE Transactions on Image Processing， 2005， 14（7）: 960-972.

［13］ 袁志辉， 邓云凯， 李飞， 等. 改进的基于最大似然估计的多通道InSAR高程重建方法［J］. 电子与信息学报， 2013， 35（9）: 2161-2167. Yuan Zhi-hu i， Deng Yun-kai， Li Fei， et al.. Im p roved m ultichannel InSAR height reconstruction m ethod based on maximum likelihood estimation［J］. Journal of Electronics & Information Technology， 2013， 35（9）: 2161-2167.

［14］ 于瀚雯， 保铮. 利用L1范数的多基线InSAR相位解缠绕技术［J］. 西安电子科技大学学报， 2013， 40（4）: 37-41. Yu Han-wen and Bao Zheng. L1-norm m ethod for mu lti-baseline InSAR phase unw rapp ing［J］. Journal of Xidian University， 2013， 40（4）: 37-41.

［15］ Yu Han-wen， Xing M eng-dao， and Bao Zheng. A fast phase unw rapping method for large-scale interferogram s［J］. IEEE Transactions on Geoscience and Remote Sensing， 2013， 51（7）: 4240-4248.

［16］ Yu Han-wen， Li Zhen-fang， and Bao Zheng. Residues cluster-based segmentation and outlier-detection method for large-scale phase unw rapping［J］. IEEE Transactions on Image Processing， 2011， 20（10）: 2865-2875.

［17］ Chen C and Zebker H A. Network app roaches to two-dimensional phase unw rapping: intractability and two new algorithms［J］. Journal of the Optical Society of Am erica A， 2000， 17（3）: 401-414.

［18］ Ghiglia D and Romero L. M inimum Lp-norm two-dimensional phase unw rapping［J］. Journal of the Optical Society of America A， 1996， 13（10）: 1999-2013.

刘会涛： 男，1986年生，博士生，研究方向为InSAR成像及相位解缠绕.

邢孟道： 男，1975年生，教授，博士生导师，研究方向为雷达成像和目标识别.

保 铮： 男，1927年生，中国科学院院士，博士生导师，研究方向为雷达信号处理.

L L∞+1-norm M ethod for M u lti-baseline Phase Unw rapping

Liu Hui-tao Xing Meng-dao Bao Zheng
（National Laboratory of Radar Signal Processing， X idian University， X i’an 710071， China）

M ulti-baseline phase unw rapping p roblem can be solved according to find the optimal solution of the L1-norm optim ization. However， there are two prob lem s: one is the huge memory required and the other is the difficulty in processing interferograms w ith severe noise. In order to decrease the memory requirement of the L1-norm m ethod， w ith a cost function of L∞-norm is em p loyed to approximate the L1-norm. Consequently， the ob jective function of the im proved mu lti-baseline phase unw rapping is the form of L∞-norm+L1-norm， and the size of the new optim ization variable is decreased by 57%. The performance of the proposed algorithm is validated via a real dataset w ith severe noise p resent， and the experiment demonstrates that the proposed algorithm not only presents a well phase unw rapping resu lt of interferograms with good quality， but also perform s a filtering against noise region.

Interferometric SAR （InSAR）； Mu lti-baseline； Phase unw rapping； L1-norm； L∞+ L1-norm

TN957.52

：A

：1009-5896（2015）05-1111-05

10.11999/JEIT 140955

2014-07-17收到，2015-01-06改回

国家自然科学基金优秀青年基金（61222108）资助课题*通信作者：邢孟道 xm d@xidian.edu.cn