一种改进的基于低秩逼近的空时自适应处理算法
解 虎冯大政虞泓波袁明冬聂卫科
①(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)
②(西北大学信息科学与技术学院 西安 710127)
一种改进的基于低秩逼近的空时自适应处理算法
解 虎*①冯大政①虞泓波①袁明冬①聂卫科②
①(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)
②(西北大学信息科学与技术学院 西安 710127)
针对非均匀杂波情况下的空时自适应处理的小样本问题,该文提出一种基于权矩阵低秩逼近的空时自适应处理方法。与传统的低秩逼近算法不同,利用空时导向矢量特殊的克罗累计性,该文重新构造新的权矩阵,使得该权矩阵的行数与列数尽可能地相近或相同,以减少算法所需的样本个数和计算量。采用低秩逼近方法对新构造的权矩阵进行表示,则原二次优化问题转化为求解一个双二次代价函数问题。实验表明,改进的空时权矩阵低秩逼近方法能有效地提高空时自适应处理的收敛速度和降低算法复杂度。
机载雷达;空时自适应;低秩逼近;杂波抑制;双迭代
1 引言
机载预警雷达不论对空或对地进行动目标检测,关键在于对于地杂波的抑制,对于机载雷达,雷达载体在运动,整个大地相对于雷达存在相对运动,会产生相应的多普勒偏移,即地杂波会在整个多普勒域展宽,具有与信号相同的多普勒频率特性,动目标将会被严重地抑制进而难以检测。然而利用地杂波方位与多普勒的空时耦合性,对接收信号进行空域与多普勒域的两维联合自适应处理,可以将杂波滤除。阵元与脉冲的两维自适应处理通常称作空时自适应处理(Space-Tim e Adaptive Processing,STAP)[1]。
传统的空时自适应处理在实际应用中,面临两方面的挑战。一是计算量大,由于STAP是对空域和时域两维联合自适应处理,其维数是空域维数(阵元个数N)和时域维数(脉冲个数M)的乘积MN,因此需要对MN MN×的协方差矩阵进行求逆,实际中难以实时实现;二是所需样本巨大,为获得接近于(3 dB的性能损失)最优STAP处理性能(协方差已知)所需要的与待检测单元独立同分布样本个数是空时维数MN的两倍,而实际中只有靠近待检测单元少数样本近似满足独立同分布条件。尤其在非均匀杂波背景下,可用样本更少。导致杂波样本非均匀的因素很多,一般主要分成两部分:幅度不均匀(地形以及其覆盖物变化,强散射点等),多普勒谱展宽(水面,森林受风影响导致)[2,3]。针对样本不足问题,人们提出了很多不同的降维空时自适应处理方法,例如著名的辅助通道法(Auxiliary Channel Receiver ACR), FA(Factored A lgorithm), EFA[4](Extended Factored A lgorithm)和JDL[5](Joint Domain Localized)方法等。此类降维方法主要思想是将数据通过傅里叶变换将数据转化到低维空间,再进行自适应处理。通过降维处理有效地降低了算法的计算量和所需样本数目。
为了进一步提高杂波抑制性能,必须增加自适应权的自由度,即增加降维后的维数,但训练样本数和计算复杂度也会相应增加。因此,研究权矢量自由度高、样本要求和计算复杂度低的降维STAP处理方法是必要的。文献[6]提出一种空时可分离自适应杂波抑制方法,该方法以经典的最小方差无畸变(M inimum Variance D istortion less Response,MVDR)准则[7]为基础,建立了关于空域权向量和时域权向量的双二次代价函数,然后采用双迭代算法(Bi-Iterative A lgorithm, BIA)求解自适应权。文献[8]提出一种基于低秩逼近的空时双边二次代价函数,该方法比文献[6]具有更多的自由度,因此算法性能更好,且计算量小。文献[6,8]算法收敛所需的样本个数为2max{M, N},而对于大部分空时自适应系统,阵元个数和一个相关时间内的脉冲数并不在一个数量级,即M≫ N,此时双迭代算法所需要的样本个数依然很多。不仅对于传统STAP系统,对于M IMO-STAP[9,10]系统这一现象更加普遍,由于存在虚拟阵元,因此一般M≪ N。因此本文提出一种改进的基于权矩阵低秩逼近的双迭代算法,该算法通过重新构造新的自适应权矩阵,使得权矩阵的行数与列数尽可能相等,从而降低相应的协方差矩阵的维度,提高收敛速度以及降低计算复杂度。
2 STAP信号模型和传统空时可分离杂波抑制方法
假设天线阵列为均匀线阵结构,阵元个数为N,一个相干处理时间内接收到的脉冲个数为M,则某一距离环接收到的NM×1数据向量可以排列为矩阵形式,即
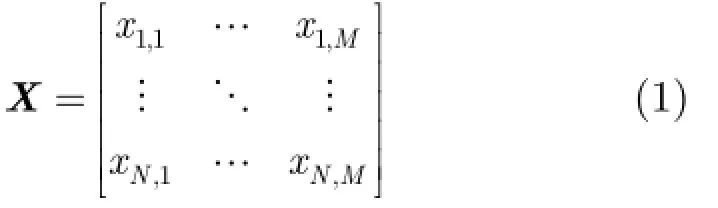
其中xn,m表示第n个阵元接收到的第m次回波。最优空时自适应处理器本质上是求解式(2)的二次优化问题:

其中w为2维空时权矢量,vec(·)表示矩阵的向量化,空时可分离自适应处理器(Space Time Separable Filter, STSF)将空时权表示为式(3)的形式

其中v∈ CM×1,u∈ CN×1为对应的时域权和空域权。将式(3)代入式(2)得到如下双二次优化方程:

采用拉格朗日乘子法,式(4)可以转化为无约束的双二次代价函数:

其中λ为拉格朗日乘子,代价函数J(u, v,λ)相对于u和v分别是二次的,此外对式(5)进行分析可知,代价函数J(u, v,λ)的解存在尺度模糊问题,即

根据文献[6]可知,利用双迭代算法可以求解式(5)且能有效地处理尺度模糊问题,理论证明双迭代算法能收敛到最优解[11,12],且算法收敛所需要的样本数目为2m ax{N, M}。双迭代方法是将一个双二次代价函数转化为两个单边二次代价函数,假定其中一个单边二次代价函数的解已知,求解另一组解,然后采用交替迭代的方法进行求解直至算法收敛。另外,由式(5)可知空时可分离方法的自由度为N+ M-1,然而对于某些非均匀杂波,杂波的自由度大于N+ M-1,因此为了得到更好的杂波抑制性能,需要增加传统空时可分离算法的自由度。
3 基于空时重构的低秩逼近方法
由上述推导可知空时可分离的双迭代算法相比较传统的空时全维自适应算法,大幅提高收敛速度和降低计算复杂度。但是当系统的时域维度或空域维度较大时,STSF算法所需要的样本数目2m ax{N, M}(M≪ N或者M≫ N)依然难以得到满足。本文对数据矩阵进行重排,构造新的数据矩阵和权矩阵,为了增加算法的自由度,采用低秩逼近方法来提高自适应权的自由度,从而达到更快的收敛速度。假设存在正整数NM且N,M尽可能相近,那么数据矩阵可以重新排列为


与新构造的数据矩阵相对应的N× M维的自适应权矩阵写为

式(17)中有D( N+ M)个独立变量,而且有D( D-1)+1个约束条件,式(16)表明特征向量之间存在D个相互关系,因此代价函数的自由度为

特别的当D=m in( M, N)时,式(17)的自由度为,即空时全维自适应处理。
4 多阶段法
求解式(17)的关键是如何处理正交约束问题,这里采用多阶段降维方法来消除正交约束,令

为了简化公式,令

那么,式(21)可以等价为

显然式(24)为双二次代价函数的标准形式,可以采用双迭代方法进行求解,在此不再赘述[11,12]。


图1给出了所提算法的实现流程图,可以看出与多级维纳滤波处理一样,具有很好的格型结构。此外,如果使用降维矩阵P,F的特殊结构,图中矩阵相乘的操作可以通过几个矩阵乘以向量的方式执行,计算量较小。
5 计算量分析
为了估计改进的低秩逼近空时自适应处理(Improved Low-Rank Approxim ation STAP, ILRASTAP)算法的计算复杂度,首先需要确定ILRASTAP新构造的数据矩阵维度,所需要的样本个数L,双迭代算法所需要的迭代次数K和分解阶数D。在ILRA-STAP算法中,所用到的最大的相关矩阵的维数为max(N, M),为了保证该矩阵尽可能非奇异,L≥2max( N, M)。另外,由文献[11]可知双迭代算法具有快速收敛性,一般5~10步即可收敛。实验表明,分解阶数一般取3就可以获得很好的性能,因此取D=3。

图1 所提算法流程示意图
根据文献[8],忽略一些低阶项,可以直接得到ILRA-STAP的总计算量为其主要计算量来自其中维数最大的相关矩阵的求逆,即同样传统的LRA-STAP的主要计算量为为了进一步说明ILRASTAP的计算量,以实例进行分析,假设N=8, M=128,重排后得到的数据维度本文算法的主要计算量为O(323),而传统的LRASTAP的主要计算量为O(1283),显然本文算法的计算量相较于LRA-STAP得到大幅下降。另一方面,本文对权矩阵进行了重排,不仅降低了算法的计算量,同时也降低了算法所需的样本数目,即仅需2× 32= 64个样本算法即可收敛,而传统LRASTAP需要2× 128= 256个样本。
6 仿真实验
实验1 在理论推导的基础上,本节通过仿真实验验证双迭代算法在空时重构后的快速收敛性,同时比较本文算法与传统的FA, EFA算法的杂波抑制性能。仿真实验采用8× 8的方阵阵列结构(在俯仰上进行列合成),雷达工作波长λ=0.23 m ,阵元间距d= 0.115 m,载机速度V=115 m/s,飞行高度H=3 km,一个相干处理时间内的脉冲数为128,输入杂噪比CNR=60 dB。
图2所示为ILRA-STAP算法在各个阶段迭代处理中改善因子随迭代次数的变化曲线,其中归一化多普勒fd=0.2,位于主杂波区。由图2可以看出,在每一个阶段中,双迭代算法均有快速收敛性,迭代5~7次即可收敛。而且随着阶段的加深,性能逐渐得到了改善,但是改善的程度也越来越小。第2阶段较第1阶段有2.5 dB增益,而第3阶段仅比第2阶段高0.5 dB。图3为本文算法在D不同时的改善因子对多普勒通道变化曲线,并与传统的FA,EFA, STSF和传统的低秩逼近(Low-Rank Approximation, LRA)算法作为参考,样本个数L= 150。由图可知,本文算法(D=3)与EFA算法在主杂波区性能相近,在其余多普勒通道略优于EFA,而当D=1时,本文算法略差于EFA方法,但是明显优于FA算法,传统的低秩逼近算法由于样本不足,因此其性能较差。
图4所示为本文算法在D不同时的空时2维频率响应,归一化空域频率为0,归一化多普勒频率为fd= 0.5。图4(a)给出当D=1时,ILRA的空时2维频率响应图,ILRA算法在主杂波区形成了较深的凹口,可以对其有效抑制,但由于自适应自由度有限,在多普勒域出现了栅瓣。随着D增加,栅瓣的影响越来越小,且在主杂波脊上形成的凹口更宽更深,如图4(b)所示(D=3)。
实验2 本实验采用常用的MCARM实测数据验证本文提出的ILRA-STAP算法的杂波抑制性能。MCARM数据是由美国空军Rome实验室90年代,为研究空时自适应算法而录取的一批相控阵机载雷达数据,具体参数见文献[8]。本实验主要处理编号为RL050575数据中300~500号距离门,为了便于本文算法实现,采用其中11个均匀线性子阵的前99个脉冲的数据,且在第400和420号距离单元均注入一个信杂噪比为-40 dB的动目标信号,该目标的空域频率为0(位于主瓣波束内),归一化多普勒频率为0.1(位于主杂波区附近)。动目标检测性能由目标信号高出残余杂波噪声功率值,即输出信杂噪比(Signal to Clutter and Noise Ratio, SCNR)来评估。对于本文算法,本实验采用。以最大限度的降低所提算法的计算复杂度。

图2 ILRA算法在不同阶段随迭代次数的性能曲线

图3 改善因子图

图4 空时频率响应特性
图5 给出了本文所提的ILRA-STAP算法、传统的低秩逼近算法(LRA), STSF和 EFA算法处理MCARM数据的输出结果,其中EFA算法选取与待检测多普勒通道相邻的两个多普勒通道作为辅助通道进行联合自适应处理。图5(a)和图5(b)联合比较各算法的性能,并且以EFA方法的性能为参考。可以看出,几种算法均能有效地滤除杂波,将动目标信号从残余背景杂波噪声中提取出来。由图5(a)可以看出当D=1时,本文算法与传统STSF和EFA性能相当(L=200),但是计算量明显得到减少;当满足独立同分布(Independent Identical Distribution,IID)样本足够多时,STSF方法的性能会优于本文算法,而在实际中,IID样本数十分有限。图5(b)所示为当D=3时,本文算法(ILRA), LRA和EFA方法的对比结果,显然本文算法和LRA对杂波的抑制效果相当,但要优于EFA,也就意味着相同条件下较EFA算法有较高的检测概率。在IID样本较少时,ILRA方法会略优于LRA方法,且其ILRA的计算量要明显小于LRA,因此本文算法适用于高维小样本情况。
7 结束语
对于传统的空时可分离自适应处理,当空域维度与时域维度不在同一数量级时,其算法收敛所需要的样本数目以及计算复杂度都明显增加。所提算法利用目标空时导向矢量可以改写为两个维度相当的向量的K ronercker积的特性,对传统的空时可分离自适应处理方法进行了改进,显著提高了算法的收敛速度以及降低了算法的计算复杂度,使得本文算法可适用于高维小样本系统。仿真实验和实测数据处理结果均验证了算法的有效性。
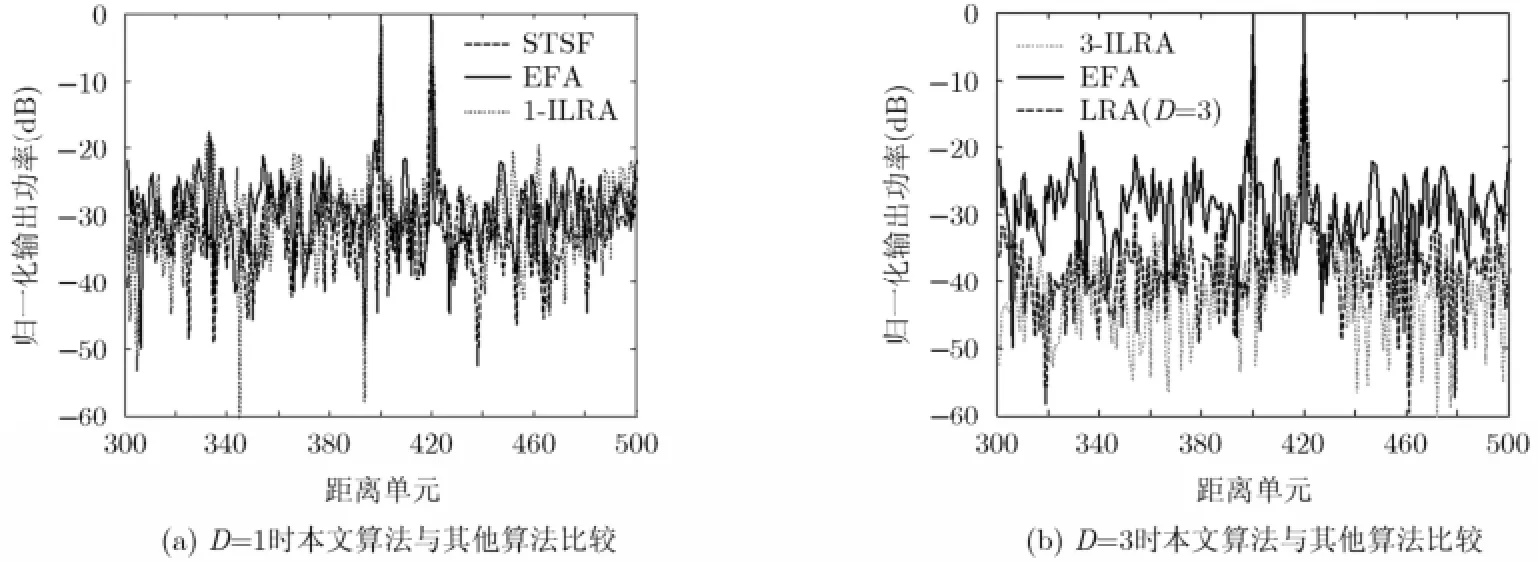
图5 归一化输出随距离单元变化曲线
[1] Melvin W L. A stap overview[J]. IEEE Aerospace and Electronic System s Magazine, 2004, 19(1): 19-35.
[2] Yang X, Liu Y, and Long T. Robust non-hom ogeneity detection algorithm based on prolate spheroidal wave functions for space-time adap tive processing[J]. IET Radar,Sonar & Navigation, 2013, 7(1): 47-54.
[3] Meziani H A and Soltani F. Performance analysis of some CFAR detectors in homogeneous and non-homogeneous Pearson-distributed clutter[J]. Signal Processing, 2006, 86(8): 2115-2122.
[4] DiPietro R C. ?Extended factored space-time processing for airborne radar system s[C]. Proceedings of the ?IEEE Conference on Signals, System s and Com puters, ?Asilomar,Pacific Grove, Canada, 1992: 425-430.
[5] W ang H and Cai L. On adaptive spatial-tem poral processing for airborne surveillance radar system s[J]. IEEE Transactions on Aerospace and Electronic Systems, 1994, 30(3): 660-670.
[6] Li X M, Feng D Z, Liu H W, et al.. Spatial-tem poral separable filter for adaptive clutter suppression in airborne radar[J]. Electronics Letters, 2008, 44(5): 380-381.
[7] Bai M R and Benesty J. Acoustic A rray System s: Theory,Im p lem entation, and App lication[M]. New York: John W iley and Sons, 2013: 287-313.
[8] Li X M, Feng D Z, Liu H W, et al.. Dimension-reduced spacetime adaptive clutter suppression algorithm based on lower rank approximation to weight matrix in airborne radar[J]. IEEE Transactions on Aerospace and E lectronic Systems,2014, 50(1): 53-69.
[9] 党博, 廖桂生, 李军, 等. 基于投影权优化的双基地M IMO雷达杂波抑制方法[J]. 电子与信息学报, 2013, 35(10): 2505-2511. Dang Bo, Liao Gui-sheng, Li Jun, et al.. Weighted p rojection optim ization for range-dependent clutter suppression in b istatic M IMO radar[J]. Journal of E lectron ics & Inform ation Technology, 2013, 35(10): 2505-2511.
[10] Li H, Li Y, and He Z. M IMO radar clutter m itigation based on joint beam form ing and joint domain localized processing[J]. EURASIP Journal on W ireless Comm unications and Networking, 2013, 2013(1): 1-10.
[11] Feng D Z, Li X M, Lü H, et al.. Two-sided m inim um-variance distortionless response beam former for M IMO radar[J]. Signal Processing, 2009, 89(3): 328-332.
[12] Feng D Z, Zhang H, and Zheng W X. Bi-iterative algorithm for extracting independent com ponents from array signals[J]. IEEE Transactions on Signal Processing, 2011, 59(8): 3636-3646.
[13] Ottaviani G, Spaen lehauer P J, and Sturm fels B. Exact solutions for structured low-rank approximation[OL]. http: arxiv.org/abs/1311. 2376, 2013.
[14] Lee J, K im S, Lebanon G, et al.. Local low-rank m atrix approxim ation[C]. Proceed ings of the 30th International Conference on Machine Learning, Atlanta, USA. 2013: 82-90.
[15] 李晓明, 冯大政. 一种机载雷达两级降维空时二维自适应处理方法[J]. 航空学报, 2008, 29(1): 170-175. Li Xiao-m ing and Feng Da-zheng. A two stage dimensionreduced STAP M ethod for airborne radar[J]. Acta Aeronautica et Aastronautica Sinica, 2008, 29(1): 170?-175.
解 虎: 男,1987年生,博士生,研究方向为阵列信号处理和空时自适应信号处理.
冯大政: 男,1959年生,博士,教授,博士生导师,研究方向为雷达信号处理、信号参数估计、仿大脑信息处理、场景感知、模式识别等.
虞鸿波: 男,1988年生,博士生,研究方向为阵列信号处理和空时自适应信号处理.
An Improved Space-time Adaptive Processing A lgorithm Based on Low Rank App roximation
X ie Hu①Feng Da-zheng①Yu Hong-bo①Yuan M ing-dong①Nie Wei-ke②①(National Laboratory of Radar Signal Processing, X idian University, X i’an 710071, China)
②(School of Information and Technology, Northwest University, Xi’an 710127, China)
To handle the small sam ple support p roblem under the heterogeneous clutter environment, a fast convergence Space-Time Adap tive Processing (STAP) algorithm based on low-rank app roximation of the weight matrix is proposed. Un like the traditional Low-Rank Approximation (LRA) algorithm for STAP, the weight matrix is reconstructed so that the numbers of its columns and rows are the same or close to each other by utilizing the special Kronecker property of the space time steering vector, which to reduce the requirement of sam ples and computational load. By using the low-rank approximation method to approximate the adaptive weight matrix, the original quadratic op timal problem transform s into a bi-quadratic op timal problem. Experimental results verify that the Im p roved LRA (ILRA) m ethod can im prove the convergence rate and reduce the com pu tational load.
A irborne radar; Space-T im e Adaptive Processing (STAP); Low-Rank App roxim ation (LRA); Clutter supp ression; Bi-iterative
TN959.73
: A
:1009-5896(2015)05-1051-07
10.11999/JEIT 140832
2014-06-23收到,2014-12-29改回
国家自然科学基金(61271293)和陕西省自然科学基金(2013JM 8008)资助课题
*通信作者:解虎 xiehumor@gmail.com

